帶有稀疏執行器故障的事件觸發網絡化系統容錯控制

關燕鵬　張文婷　平國楠

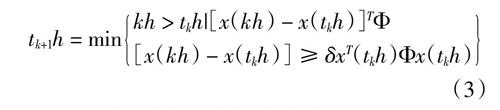
摘? ?要：針對一類具有事件觸發信息傳輸機制的網絡化控制系統，對系統故障執行器個數進行稀疏約束，研究系統在有限個執行器失效情況下的指數穩定及控制器設計問題。將系統故障執行器個數的約束轉化為對控制器增益矩陣行的勢約束，利用混合整數方法來解決這類稀疏約束的容錯控制問題。在此基礎上，利用Lyapunov泛函方法，得出閉環系統在有限個執行器失效情況下系統呈指數穩定的充分條件以及具有行稀疏約束的控制器設計方法。最后，通過一個飛行控制系統的數值仿真實例驗證所提控制方法的可行性和有效性。

關鍵詞：網絡化控制系統;事件觸發傳輸機制;執行器故障;稀疏約束;容錯控制

中圖分類號：TP273? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A

Fault-tolerant Control of Event-triggered Networked

System Based on Sparse Actuator Fault

GUAN Yan-peng？覮，ZHANG Wen-ting，PING Guo-nan

（Department of Automation，Shanxi University，Taiyuan，Shanxi 030006，China）

Abstract：For a class of networked control systems with event-triggered information transmission mechanism，the number of fault actuators is sparsely constrained，and the exponential stability and controller design of the system with a limited number of actuator failures are studied. The contribution is to convert the number of fault actuators to a cardinality constraint on the controller gain matrix. The mixed integer programming is used to solve this kind of sparse constraint problem. By using the Lyapunov functional method，we obtained a sufficient condition for the closed loop system to be exponentially stable with a limited number of actuator failures and a controller design method with row sparse constraints is also presented. Finally，the effectiveness of the proposed method is verified by a numerical simulation example about a flight control system.

Key words：networked control systems;event-triggered transmission mechanism;actuator failure;sparse constraint;fault-tolerant control

控制系統是由被控對象、控制器、傳感器、執行器以及計算機軟硬件組成的閉環系統，系統的各個環節都有可能發生故障，據統計，80%以上的控制系統故障都是由執行器或傳感器發生故障所導致，所以在設計系統時如果不考慮控制系統的某些部件（如傳感器或執行器等）在其運行過程中發生故障或失效對系統的影響，那么一旦出現故障就有可能導致系統性能下降或系統不穩定，甚至導致整個系統崩潰，由此帶來的損失是無法估量的，所以容錯控制理論正成為控制理論與控制工程的研究熱點[1-10]。近幾年，許多研究者都在進行故障容錯控制方面的研究[11-17]。例如文[11]研究了一類具有干擾和執行器故障的不確定大規模互聯系統的分散自適應容錯控制問題，故障類型包括卡滯、停電和失效。文[12]針對一類具有隨機執行器故障的網絡化T-S模糊系統，提出一種能有效減少數據傳輸量的事件觸發機制。文[13]研究一類具有輸出擾動的離散時間切換系統的執行器故障檢測問題。文[14] 研究了串聯同軸管道風扇飛機在系統不確定，不匹配擾動以及執行器飽和情況下的魯棒自適應容錯控制問題。文[15]針對一類具有執行器故障的非線性系統，提出基于線性矩陣不等式的一體化魯棒主動容錯控制器設計方法。

目前文章中執行器故障的表現形式主要分以下兩類，第一類為執行器故障情況隨時間而改變，如文[16]針對一類帶有執行器故障的不確定線性系統，設計帶有參數更新律的自適應H無窮容錯控制器，其執行器故障模式為uF（t） = u（t） + F（t），F（t）為其時變故障向量;第二類為引入故障開關陣F = diag{f1，f2，…fn}，fi值為1，代表第 個執行器正常，值為0，代表第i個執行器失效。如文[17]針對一類網絡誘導時滯模型，設計狀態反饋形式的自適應容錯控制器，執行器故障模式表示為uF（t）=（1-ρ）u（t），其中ρ = diag{ρ1，ρ2，…，ρn}，ρi∈{0，1]是未知常數，ρi = 1和ρi = 0分別代表第i個執行器故障或正常。

容錯控制可分為主動容錯和被動容錯兩大類別。主動容錯控制需要在線提取故障診斷信息，所設計的控制器結構和參數均需要在線調整，目前應用最為廣泛的主動容錯方法為自適應容錯控制，此方法可以有效應對各種故障類型，在線動態彌補故障情況，進而設計出期望的系統性能，但自適應率對于故障的估算通常會消耗大量的計算信息和計算時間，且自適應系統自身也存在非線性特性，而這些問題均會削弱系統的容錯效果。被動容錯即設計一個控制器，其結構和參數都是恒定的，不需要在線調整，在設計系統之前就已經考慮了系統可能發生的故障，系統不包含故障檢測和隔離單元，具有易于實現的優點，但同時也增加了系統的保守性，魯棒容錯控制就是一種典型的被動容錯方法。

值得指出的是，無論是主動容錯還是被動容錯，目前所提出的系統故障模型大多為傳感器或執行器發生故障，且隨機設定故障傳感器或執行器，均沒有考慮對傳感器或執行器故障個數進行稀疏約束的問題，針對這類問題，本文對一類帶有稀疏執行器故障的事件觸發網絡化系統進行容錯控制，將故障執行器個數的約束轉化為對系統控制器增益矩陣行的勢約束，利用混合整數方法來解決這類帶有稀疏約束的容錯控制問題，結合Lyapunov泛函方法以及矩陣變換，得到使系統呈指數漸近穩定的充分條件以及具有行稀疏約束的控制器設計方法，并通過數值例子證明此方法的有效性。

2? ?問題描述

考慮如下一類線性系統：

（t） = Ax（t） + Bu（t）? ? ? y（t） = Cx（t）? ? ? ? （1）

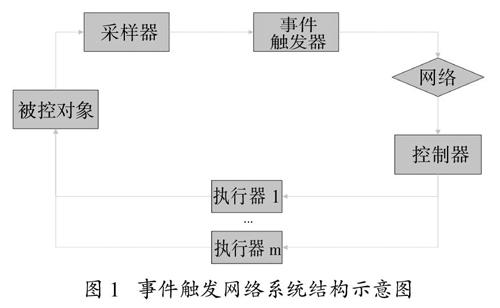
其中：x（t）∈Rn為系統狀態向量，u（t）∈Rm為系統的控制輸入向量，y（t）∈RT為被控輸出量，A、B、C為適當維數的常數矩陣，系統初始條件為x（0） = x0。在本文中，我們利用采樣周期為h的采樣器來測量狀態x（t），為了充分利用網絡資源，減少冗余數據的傳輸和計算，并非所有測量狀態都將用于反饋控制，為此，我們提出一種基于事件觸發的信息傳輸機制來確定狀態測量值是否被傳遞給控制器，以用于控制輸入計算。其系統結構圖如圖1所示：

圖1? ?事件觸發網絡系統結構示意圖

系統的采樣時刻序列為{kh}∞1，而被傳輸的數據采樣時刻序列為{tkh}∞1，為了更好地說明問題，不考慮信號采樣和傳輸過程中的時延問題，但對于具有時延的網絡控制系統，所提出的方法同樣適用。在當前采樣狀態值x（kh）與最近一次被傳輸的采樣狀態值x（tkh）之間的誤差突破事件觸發閥值條件時，當前采樣狀態值才可被傳輸，本文所采用的事件觸發條件如式（2）所示：

[x（kh） - x（tkh）]TΦ[x（kh） - x（tkh）] <

δxT（tkh）Φx（tkh）? ? ? ? （2）

其中，Φ > 0為加權矩陣，δ∈（0，1）為事件閥值參數。那么時間序列{tkh}∞1的產生可表示為如下形式：

tk+1h = minkh > tkh|[x（kh） - x（tkh）]TΦ[x（kh） - x（tkh）] ≥ δxT（tkh）Φx（tkh）

（3）

選取狀態反饋控制律，其形式為：

u（t） = Kx（tkh），t∈[tkh，tk+1h]? ? ?Cardrow（K）≤κr

（4）

Km×n是待求的控制器增益矩陣，Cardrow（K）≤κr表示矩陣的非零行個數不超過κr個，全零行的個數不少于 m - κr個，1≤κr≤m，即意味著系統故障執行器個數不少于m-κr個。換言之，當控制器增益矩陣非零行個數為κr時，系統需要選取κr個執行器保持工作以維持系統所需的性能。當κr值越小即意味著系統在保持一定性能指標的前提下所需執行器的個數越少，系統的容錯能力越強，從而可以節省網絡資源，降低成本。在區間t∈[tkh，tk+1h）內，定義：

rk，ih=tkh+ih，i∈Ω：=0，1，2，…，tk+1-tk-1（5）

e（rk，ih） = x（rk，ih） - x（tkh）? ? ? ? （6）

當t∈[tkh，tk+1h），i∈Ω時，令η（t） = t - rk，i h，那么，0≤η（t）

x（tkh）=x（t-η（t））-e（rk，ih），t∈[tkh，tk+1h]? （7）

根據式（4）可將帶有執行器故障的事件觸發閉環系統表示為：

（t） = Ax（t） + BKx（t - η（t） -BKe（rk，i））

y（t） = Cx（t），t∈[tkh，tk+1h]? ? （8）

Cardrow（K） ≤ κr

目標是設計如式（4）所示的行稀疏狀態反饋控制器增益矩陣K，將系統故障執行器個數的約束轉化為對控制器增益矩陣行的勢約束，使得閉環系統（8）在有限個執行器失效的情況下達到指數漸近穩定。

3? ?主要結果

在本節中，將給出閉環系統（8）呈指數漸近穩定的充分條件，以下引理將被用于主要結果的推導：

引理1[18]：Y，R為適當維數的矩陣，R>0，存在常數h>0，η（t）∈[0，h），且可積函數■（t）：[-h，0]→Rn，如果矩陣R? ? ?YYT? ? R > 0成立，那么不等式（9）即可成立。

-h■■（v）R■（v）dv ≤ ξT（t）πξ（t）? ? ? ? （9）

其中

ξ（t） =? ? ? x（t）x（t - η（t））? ?x（t - h），π =-R? ? ?R + Y? ? ? -Y *? -2R-Y-YT? R+Y *? ? ? ? ? *? ? ? ? ? ?-R

（10）

*表示對稱矩陣中的對稱項。

實現對控制器增益矩陣行的勢約束是關鍵部分，根據文[19]中關于向量零范數等效轉換的論述，本文對矩陣的行稀疏約束進行如下處理。

引理2[19]：對于一個矩陣K∈Rm×n，假設矩陣 中各元素絕對值的最大值不超過M，即矩陣滿足條件‖K‖≤M，M是一個正數，如果不等式Cardrow（K）≤κr成立，則存在一個二進制序列bi∈{0，1}，i = 1，2，…，m，使得不等式（11）成立。

K（i，j） ≤ M（1 - bi），■bi ≥ m - κr? ? ?（11）

證明：必要性：因為Cardrow（K）≤κr，其代表矩陣K非零行的個數r（K）≤κr，所以m-r（K）≥m-κr。定義一個二進制序列bi，當矩陣K第i行為非零行，bi值為0，當矩陣K第i行為全零行，bi值為1，則容易驗證■bi = m-r（K）≥m-κr。又因為‖K‖≤M，所以bi為0時，K（i，j）≤M，bi為1時，K（i，j） = 0，所以，K（i，j）≤M（1 - bi）。

充分性：由于K（i，j）≤M（1 - bi）且bi是一個二進制序列，所以當bi為1時，可使矩陣K第i行為全零行，那么■bi即代表矩陣K全零行的個數。因為■bi ≥ m-κr，則表明矩陣K全零行的個數不少于m-κr個，也表明矩陣K非零行的個數不多于κr個，即Cardrow（K）≤κr，證畢。

通過這樣的方法將稀疏約束條件轉化為混合整數規劃問題，利用Matlab中intlinprog函數即可有效地解決這類求解問題。

下面將給出閉環系統（8）的穩定性條件，并利用此條件給出容錯控制器的設計方法。

定理1：給定的標量α > 0，σ > 0，δ∈（0，1），h > 0以及一個滿足1≤κr≤m的整數，如果存在實矩陣P > 0，Q > 0，R > 0，以及具有適當維數的矩陣Y，K，且存在一個標量M > 0以及一個二進制序列bi∈{0，1}，i = 1，2，…，m，使得下列不等式成立：

（13）

其中Γ11 = AP + PAT + 2αP + Q - e-2αhR，則帶有稀疏執行器故障的事件觸發網絡控制系統在衰減速率為α的情況下呈指數穩定，且K = KP-1，并滿足條件Cardrow（K）≤κr。

證明：選取如下李雅普諾夫函數：

V（t，x（t）） = xT（t）Px（t）

+ ■e2α? （v - t）xT（v）Qx（v）dv

+ h■■e2α? （s- t）xT（s）R■（s）dsdv? ? （14）

其中P、Q、R為正定矩陣。

對李雅普諾夫函數關于時間t求導可得：

■（t，x（t）） = 2xT（t）P■（t）

+ ■2αe2α? （v - t）xT（v）Qx（v）dv

+ xT（t）Qx（t） + h2■T（t）R■（t）

+ h■■-2αe-2α? （s - t）■T（s）R■（s）dsdv

- h■e2α? （v - t）■T（v）R■（v）dv? ? ? ? （15） ? ? ? ? 將式（15）加上2αV（t，x（t）），可得：

■（t，x（t）） + 2αV（t，x（t））=

2xT（t）P■（t） + 2αxT（t）Px（t） + xT（t）Qx（t）+

h2■T（t）R■（t） - h■e2α? （v - t）■T（v）R■（v）dv

（16）

根據引理1可知：

-h■e2α? （v - t）■T（v）R■（v）dv ≤ e-2αhξT（t）πξ（t）

（17）

其中，

ξ（t）=x（t）x（t - η（t））x（t - h），π=-R? ? ?R + Y? ? ? ? -Y *? ? -2R-Y-YT? R+Y *? ? ? ? ? ? *? ? ? ? ? ?-R

所以式（16）可表示為：

■（t，x（t）） + 2αV（t，x（t））

≤2xT（t）P[Ax（t） + BKx（t - η（t））-BKe（rk，i）]+

2αxT（t）Px（t） + xT（t）Qx（t） + h2xT（t）Rx（t）+

e-2αhξT（t）πξ（t）? ? ? ? （18）

由事件觸發條件式（2）可知：

eT（rk，i）Φe（rk，ih）

< δ[x（t-η（t））-e（rk，ih）]TΦ[x（t-η（t））-e（rk，ih）]

其等價于：

[xT（t - η（t））? eT（rk，ih）]? δΦ? ? ? -δΦ-δΦ? （δ-1）Φx（t-η（t））? e（rk，ih）>0

（19）

結合式（18）-（19），可得如下不等式：

（t，x（t））+2αV（t，x（t））≤φ（t）（Υ+h2MTRM）φ（t）

（20）

其中，

φ（t） =? ? ξ（t）e（rk，ih），M = [A? ?BK? ?0? ?-BK]

Υ = Υ11? ? ? PBK+e-2αh（R + Y）? ? ? ? ? -e-2αhY? ? ? ?-PBK *? δΦ-e-2αh（2R + Y + YT）? e-2αh（R + Y）? ? -δΦ *? ? ? ? ? ? ? ? ? *? ? ? ? ? ? ? ? ? ? ? ? ? ?e-2αhR? ? ? ? ? 0 *? ? ? ? ? ? ? ? ? *? ? ? ? ? ? ? ? ? ? ? ? ? ? ? *? ? ? ? （δ - 1）Φ

且Υ11 = PA + ATP + 2αP + Q - e-2αhR，結合Schur補定理，可得到系統在衰減速率為α的情況下呈指數漸近穩定的一個充分條件：

R? ? ?YYT? ? R ≥ 0

Ξ = Ξ11? ? ? PBK+e-2αh（R + Y）? ? ? ? ? -e-2αhY? ? ? ?-PBK? ? ? ? ?hAT *? ? δΦ-e-2αh（2R + Y + YT）? ?e-2αh（R + Y）? ?-δΦ? ? ? ? ?hKTBT *? ? ? ? ? ? ? ? ? *? ? ? ? ? ? ? ? ? ? ? ? ? ?e-2αhR? ? ? ? ? ? 0? ? ? ? ? ? ? ?0 *? ? ? ? ? ? ? ? ? *? ? ? ? ? ? ? ? ? ? ? ? ? ? ? *? ? ? ? ? （δ - 1）Φ? ?-hKTBT *? ? ? ? ? ? ? ? ? *? ? ? ? ? ? ? ? ? ? ? ? ? ? ? *? ? ? ? ? ? ? ?*? ? ? ? ? ? ? -R-1<0

（21）

其中Ξ11 = PA + ATP + 2αP + Q - e-2αhR。

基于以上對系統穩定性的分析，可通過矩陣變換來獲得系統的控制器增益矩陣。對矩陣Ξ兩邊均乘以對角陣{P-1，P-1，P-1，P-1，I}，令P = P-1，Q = P-1QP-1，R = P-1RP-1，K = KP，Y = P-1YP-1，Φ = P-1ΦP-1，可得式（22），

Γ11? ? ? B■+e-2αh（■+■）? ? ? ? ? -e-2αh■? ? ? ?-B■? ? ? ? ? h■AT *? δ■-e-2αh（2■+■+■T）? e-2αh（■+■）? ? -δ■? ? ? ? ? h■TBT *? ? ? ? ? ? ? ? ? *? ? ? ? ? ? ? ? ? ? ? ? ? ?e-2αh■? ? ? ? ? ?0? ? ? ? ? ? ? ? ?0 *? ? ? ? ? ? ? ? ? *? ? ? ? ? ? ? ? ? ? ? ? ? ? ? *? ? ? ? （δ - 1）■? ? ? -h■TBT *? ? ? ? ? ? ? ? ? *? ? ? ? ? ? ? ? ? ? ? ? ? ? ? *? ? ? ? ? ? ? ?*? ? ? ? ? ? ? ?-R-1<0

（22）

同時得到系統的控制器增益矩陣K = KP-1。

由于矩陣中存在非線性項-R-1，且-R-1=-[P-1 RP-1]-1，為了便于使用Matlab工具箱進行求解，可將其進行如下轉換：

由于P，R為正定矩陣，必然存在參數σ使得式（23）成立，

（■ - σ■）■-1（■ - σ■） ≥ 0? ? ? ? （23）

將其展開后可得：

-PR-1■ ≤ -2σ■ + σ2■? ? ? ? （24）

所以-R-1可用-2σ■ + σ2R來替代，由此可得式（13），若式（13）成立，則式（25）即可成立。

■（t，x（t）） + 2αV（t，x（t）） < 0? ? ? ? （25）

結合引理2可知，若式（26）成立，則控制器增益矩陣K滿足稀疏約束條件，即Cardrow（K）≤κr。

■（i，j）≤M（1-bi），■bi≥m-κr? ? ? ? （26）

由此說明，基于事件觸發的稀疏執行器故障網絡化系統在衰減速率為α的情況下呈指數漸近穩定，控制器增益矩陣K = KP-1，且滿足條件Cardrow（K）≤κr，證畢。

4? ?仿真實例

為了證明所提方法的有效性，以波音747的飛機橫向動力學模型為仿真算例，其線性化模型可以描述為[20]：

■（t） = Ax（t） + Bu（t）? x（t） = [β，yr，p，？準]T? （27）

其中，β代表側滑角，yr代表偏航率，p為滾轉率，？準為滾轉角，初始條件為x（0） = [0.5，-0.8，-1， 0.8]T，u是代表三個控制信號的控制向量u = [u1，u2，u3]，分別代表三個方向舵的伺服控制系統，在40000英尺水平飛行和前進速度為774英尺/秒（馬赫0.8）的情況下，波音747橫向動力學矩陣如下：

A = -0.0558? ?-0.9968? ?0.0802? ?0.0415? 0.598? ? ? -0.115? ?-0.0318? ? ? ?0 -3.05? ? ? ? 0.388? ? ?-0.465? ? ? ? 0? ? ?0? ? ? ? ? 0.0805? ? ? ? ?1? ? ? ? ? ? 0

B = 0.00729? ?0.01? ?0.05 -0.475? ?-0.5? ?-0.3? 0.153? ? ? 0.2? ? ?0.1? ? ?0? ? ? ? ? ?0? ? ? ? 0

選擇采樣周期h = 0.1s，指數衰減率α = 0.01，增益矩陣K各元素絕對值的最大值不超過105，即M = 105，事件觸發閥值參數δ = 0.2，以κr≤2為例，利用Matlab中的LMI工具箱求解線性矩陣不等式（13），可求得增益矩陣K為：

K = -0.21759? 0.64001? 0.088754? 0.058592-0.21621? 0.64755? 0.089534? 0.058649? ? ? ? 0? ? ? ? ? ? ?0? ? ? ? ? ? ? 0? ? ? ? ? ? ? ?0

事件觸發權重矩陣Φ為：

Φ=? 0.0032619? ? ?-0.0048638? ? -0.00050473? ? -0.00067897 -0.0048683? ? ? 0.018229? ? ? ?0.0027539? ? ? ? ?0.0015164-0.00050473? ? 0.0027539? ? ? 0.00049883? ? ? ?0.00020134-0.00067897? ? 0.0015164? ? ? 0.00020134? ? ? ?0.00018582

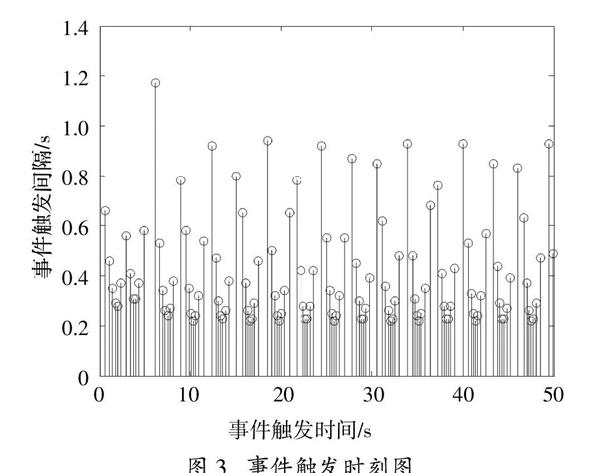
在運行時間T = 50 s情況下，系統狀態響應曲線如圖2所示，事件觸發時刻如圖3所示：

圖3? ?事件觸發時刻圖

由以上仿真結果可知，Cardrow（K） = 2，即代表系統控制器增益矩陣K有兩行為非零行，也可代表系統有一個執行器出現故障，其余兩個均正常。根據圖2可知，在一個執行器出現故障的情況下，系統仍可保持穩定，從而說明系統需選取兩個執行器保持工作以維持系統所需的性能，也可說明系統具有一定的容錯能力。在系統仿真過程為50秒的情況下，被傳輸的采樣狀態共120次，與采樣次數相比數據傳輸量明顯降低，表明帶有稀疏執行器故障的事件觸發網絡化系統可有效節省網絡資源，達到降低成本的目標。

5? ?結? ?論

提出了一種針對網絡化系統稀疏執行器故障的容錯控制設計方法。通過對控制器增益矩陣行的勢約束實現對系統故障執行器個數的稀疏約束，利用混合整數的方法解決這類稀疏約束問題，并結合李雅普諾夫泛函方法得出系統在事件觸發條件下呈指數漸近穩定的充分條件以及具有行稀疏約束控制器的設計方法，最后通過一個實際數值仿真例子驗證了所提方法的有效性。

參考文獻

[1]? ? YE S，ZHANG Y，WANG X. Fault-tolerant control for a class of uncertain systems with actuator faults[J]. Tsinghua Science & Technology，2010，15（2）：174—183.

[2]? ? WU L. Robust adaptive fault-tolerant control for linear systems with actuator failures and mismatched parameter uncertainties[J]. Iet Control Theory & Applications，2014，8（6）：441—449.

[3]? ? XU Y，TONG S，LI Y. Prescribed performance fuzzy adaptive fault-tolerant control of non-linear systems with actuator faults[J]. Iet Control Theory & Application，2014，8（6）：420—431.

[4]? ? WANG Z，RODRIGUES M. Actuator fault estimation observer design for discrete-time linear parameter varying descriptor systems[J]. International Journal of Adaptive Control & Signal Processing，2015，29（2）：242—258.

[5]? ? DEFOORT M，VELUVOLU K. Adaptive sensor and actuator fault estimation for a class of uncertain Lipschitz nonlinear systems[J]. International Journal of Adaptive Control & Signal Processing，2016，30（2）：271—283.

[6]? ? LI Y，YANG G. Robust fuzzy adaptive fault-tolerant control for a class of nonlinear systems with mismatched uncertainties and actuator fault[J]. Nonlinear Dynamic，2015，81（1—2）：1—15.

[7]? ? YE D，PARK J. Adaptive robust actuator fault compensation for linear systems using a novel faults estimation mechanism[J]. International Journal of Robust & Nonlinear Control，2015，26（8）：1597—1614.

[8]? ? 王君，姚曉婉. NNCS混合容錯控制方法[J].控制與決策，2018，33（2）：316—329.

[9]? ? SAMIR Z，HEMZA M. Actuator fault tolerant control using adaptive RBFNN fuzzy sliding mode controller for coaxial octorotor UAV[J]. ISA Transactions，2018，26（8）：256—268.

[10]? YANG P ，MA B. Fault-tolerant consensus of leader following multi-agent systems based on distributed fault estimation observer[J]. International Journal of Control Automation and Systems，2018，16（5）：1—9.

[11]? XIE C，YANG G. Decentralized adaptive fault-tolerant control for large-scale systems with external disturbances and actuator faults[J]. Automatica，2017，85（8）：83—90.

[12]? 張進，彭晨. 基于事件觸發的網絡化T-S模糊系統容錯控制[J]. 信息與控制，2016，45（1）：73—85.

[13]? DU D，XU S. Actuator fault detection for discrete-time switched linear systems with output disturbance[J]. International Journal of Control，Automation and System，2017，15（6）：2590—2598.

[14]? WANG X ，XIANG C. Robust adaptive fault-tolerant control of a tandem coaxial ducted fan aircraft with actuator saturation[J]. Chinese Journal of Aeronautics，2018，16（2）：365—378.

[15]? 劉聰，錢坤. 基于LMI的一體化魯棒主動容錯控制器設計[J]. 控制與決策，2018，33（1）：53—59.

[16]? 彭曉易，武力兵. 一類帶有執行器故障不確定線性系統的自適應H無窮控制[J]. 遼寧科技大學學報，2017，40（4）：292—297.

[17]? 鄧偉璍，費敏銳. 帶有執行器故障的網絡控制系統的自適應容錯H無窮控制[J]. 控制理論與應用，2010，27（2）：269—272.

[18]? GE X，HAN Q L. Distributed event-triggered H-infinity filtering over sensor networks with communication delays[J]. Information Science，2015，29（1）：128—142.

[19]? BURDAKOV O P，KANZOW C，SCHWARTZ A. Mathematical programs with cardinality constraints：reformulation? ?by complementarity-type conditions and a regulation? method[J]. SIAM Journal on Optmization，2016，26（1）：397—425.

[20]? TAO G，CHEN S H. An adaptive actuator failure compensation controller using output feedback[J]. IEEE Tr- ansactions on Automatic Control，2002，47（3）：506—511.