電鏟工作裝置EDEM Adams Simulink聯合動態仿真

鄒偉 程書培 楊磊 周航

摘要：針對電鏟工作裝置驅動力設計問題，使用EDEM計算挖掘阻力，計算結果與理論值一致。在Adams中建立電鏟工作裝置動力學模型，利用Simulink生成接近實際的提升和推壓位移曲線，并將EDEM輸出的挖掘阻力轉化為挖掘阻力曲線，實現Adams?Simulink聯合仿真。挖掘軌跡、驅動力仿真結果與理論計算結果一致。該方法可克服傳統計算只取個別位姿的不足，為后續設計提供依據。

關鍵詞：

電鏟; 工作裝置; 驅動力; 挖掘阻力; 聯合仿真; 動態仿真

中圖分類號：TD422.21; TP391.99

文獻標志碼：B

EDEM?Adams?Simulink dynamic co?simulation of

power shovel manipulator

ZOU Wei， CHENG Shupei， YANG Lei， ZHOU Hang

（

China Railway Engineering Machinery Research and Design Institute Co.， Ltd.， Wuhan 430066， China）

Abstract：

As to the driving force design for the power shovel manipulator， the digging resistance is calculated by EDEM， and the results agree well with the theoretical values. The dynamic model of the power shovel manipulator is built in Adams. The displacement curves of hoisting and crowding are obtained by Simulink， which is closed to the real process. The digging resistances outputted by EDEM are converted to a digging resistance curve. The co?simulation of Adams?Simulink is achieved. The simulation results of digging trace and driving force are consistent with the theoretical calculation values. This method can overcome the disadvantage of traditional calculation which only takes individual postures， and it can provide a basis for subsequent design.

Key words：

power shovel; manipulator; driving force; digging resistance; co?simulation; dynamic simulation

0?引?言

電鏟即電動機械挖掘機，是露天礦山開采系統中最關鍵的設備之一。國內外露天礦山生產規模日益擴大，對電鏟工作裝置設計提出更高的要求。研究挖掘軌跡與機構做功之間的關系可為機構優化提供依據[1?5]，對數螺旋線挖掘軌跡與挖掘機實際作業記錄的一致性已被證明[6?7]。離散元法是分析挖掘機鏟斗挖掘過程的一種有效方法。EDEM可以準確高效地求解挖掘阻力[8?9];Adams?Simulink聯合仿真是工作裝置動態分析的一種新方法，可以近似實際地模擬工作裝置的力學特性[10]。本文以某型號12 m3電鏟為例，基于EDEM求解挖掘阻力，并以此作為邊界條件施加到工作裝置的Adams動力學模型中;使用Simulink生成接近實際的復雜驅動信號，并實現Adams?Simulink聯合動態仿真;最后，將仿真值與理論值進行對比分析。

1?挖掘阻力求解

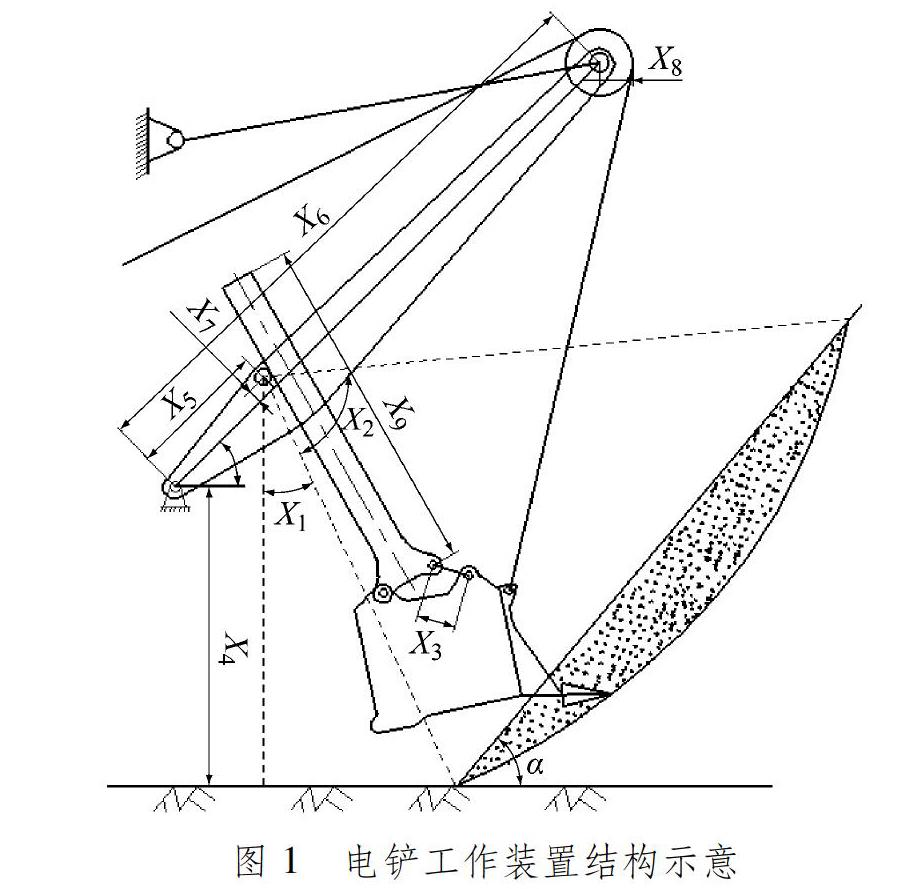
基于對數螺旋線挖掘軌跡定義鏟斗和斗桿模型的運動，電鏟工作裝置結構示意見圖1。

圖1中：X1為挖掘過程的初始角，即推壓軸中心與料堆起始點的連線與過推壓軸中心垂線的夾角;X2為斗桿的有效轉角，即從進入料堆到挖掘結束的斗桿轉角;X3為連桿長度;X4為起重臂與機架鉸接點距停機面的垂直距離;X5為起重臂下節臂長;X6為起重臂長;X7為推壓齒輪中心到起重臂中心線的距離;X8為滑輪半徑;X9為斗桿有效長度，即斗桿與連桿鉸點距斗桿尾部的距離。

對于給定機型，以上變量均為常量。斗尖的挖掘軌跡近似為以推壓齒輪中心為原點的等后角對數螺旋線，其挖掘軌跡的初始矢徑ρ0、斗桿有效轉角θ（單位為弧度）和瞬時矢徑ρ之間的關系為ρ=ρ0ekθ，其中k為斗尖矢徑與軌跡切線夾角δ的余切值，即k=

cot δ。本案例中ρ0=8 975 mm，k=0.155，挖掘終止時斗桿旋轉角度為48°。根據幾何關系和運動學關系，可以推導挖掘體積與挖掘軌跡的關系式，也可以推導各作用力表達式。最終得到的各參數表達式比較復雜，需要借助數值計算完成。

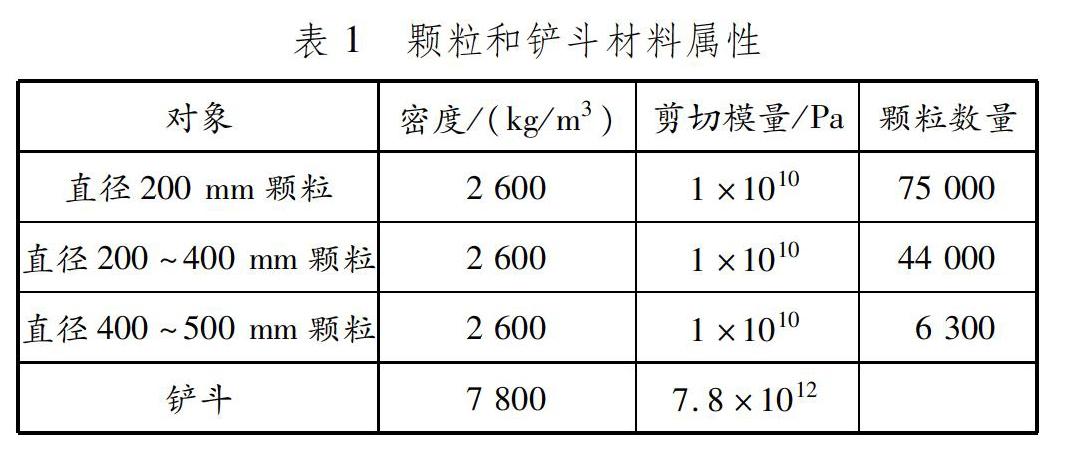
基于離散元法的EDEM能較準確地模擬挖掘過程、輸出挖掘阻力曲線并模擬多種工況，可提高計算效率且計算結果貼近實際挖掘過程，可為Adams動力學仿真提供準確的邊界條件。定義坐標系，將鏟斗和斗桿的簡化三維模型導入EDEM中，選擇爆破性能不好的礫石黏土混合物，混合物顆粒和鏟斗的泊松比分別取0.25和0.28，其材料屬性和接觸參數[8，11]分別見表1和2。

設置適當的仿真步長和仿真區域網格尺寸，挖掘過程仿真結果見圖2。在本案例工況下，顆粒生成過程在15 s內可以穩定下來，因此設置1～15 s為顆粒生成過程，16～25 s為挖掘過程，26～30 s為滿斗提升過程。挖掘阻力仿真結果與理論結果對比見圖3，理論結果是光滑曲線，EDEM仿真結果是

明顯波動的曲線，

這是由鋼絲繩柔性和挖掘阻力波動造成的。針對挖掘過程數據，對仿真結果進行最小二乘擬合，與理論結果對比發現，在25～30 s仿真曲線比較光滑，因此只需擬合15～25 s的仿真結果。仿真結果的4次多項式最小二乘擬合結果與理論結果一致。

2?Adams?Simulink聯合動態仿真

電鏟工作裝置簡化實體模型見圖4。剛性構件建模采用直接導入方式，柔性構件（鋼絲繩）利用Adams Machinery模塊中的繩索系統功能進行建模，繩索和滑輪的幾何和性能參數根據設計值確定。

構件的質量和慣量由Adams根據構件幾何模型和設定的材料參數自動計算。在Adams中建立各部件之間的約束關系，設置運動副參數，完成動力學建模。

在Adams中較難定義復雜的驅動信號，但在Simulink中較容易實現。為使仿真模型與實際工況更貼合，充分發揮各軟件的優勢，采用Adams和Simulink聯合仿真。將Adams動力學模型導出為被控對象模塊并輸入Simulink中實現聯合控制;Simulink提供Adams位移驅動函數，并在后臺啟動Adams動力學求解。

為與實際情況一致，給定推壓速度曲線為二次拋物線，得到的運動學參數可使機構受力平穩。設定挖掘時間t0=10 s，斗桿推壓距離Δc=125 8 mm，推壓加速度ac=7.5 mm/s2，則推壓位移

Sc=-act3/3+t0act2/2

（1）

根據對數螺旋線挖掘軌跡、機構幾何關系和推壓位移函數，可推導出提升位移計算公式，即

Sh=-0.436t4+1.055t3+69.933t2+3.083t+1.106

（2）

建立Simulink仿真模型，生成的挖掘阻力曲線、提升繩位移曲線和斗桿推壓位移曲線見圖5。在本案例工況下，重力加載可在1 s內達到穩定，動力學仿真無須顆粒生成過程，因此設置仿真時間為16 s，-1～0 s為系統靜平衡求解過程，1～10 s為挖掘過程，11～15 s為鏟斗滿斗提升過程，與第1節EDEM挖掘仿真時間長度完全對應。

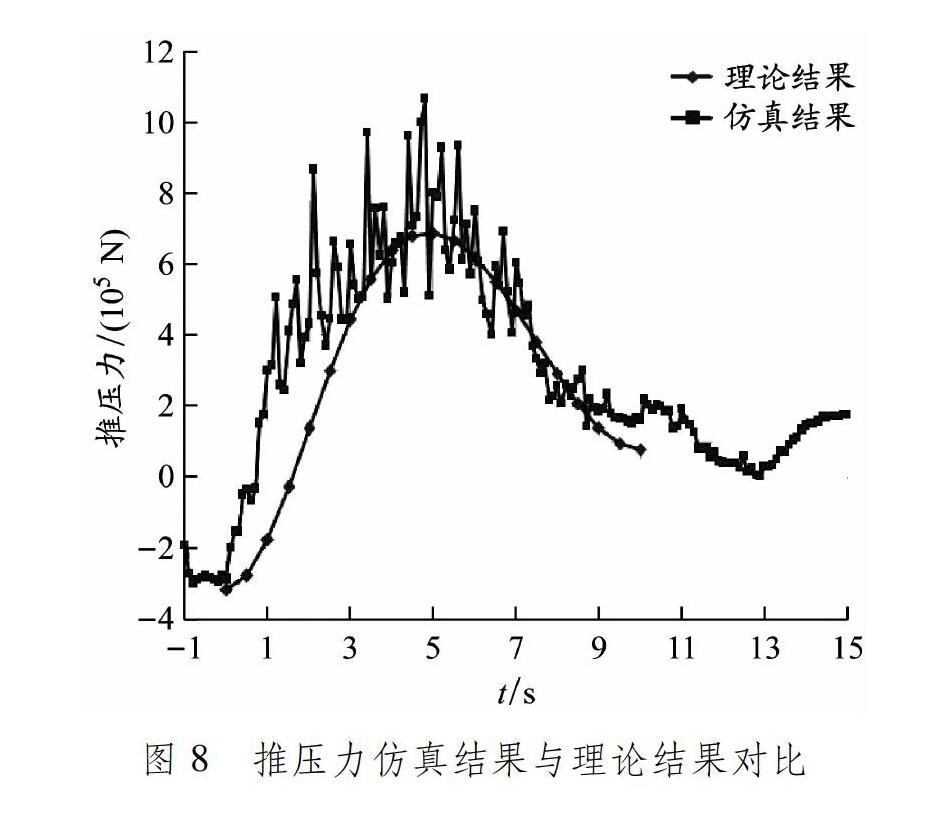
將Adams輸出的仿真結果與理論結果進行對比，見圖6～8。由圖6可以看出，動態仿真得到的鏟斗齒尖運動軌跡與理論結果一致。由圖7和8可以看出，仿真結果的最小二乘擬合曲線與理論計算結果曲線的趨勢非常接近。動態仿真的輸出結果要稍大于理論計算結果，這主要是因為動態仿真要考慮各個構件的慣性沖擊和繩索的柔韌性。最大提升力理論結果與仿真結果的相對誤差為-6.67%，最大推壓力理論結果與仿真結果的相對誤差為-5.94%，在工程設計可以接受范圍內。

3?結?論

使用EDEM較準確地計算出挖掘阻力，并將其作為邊界條件施加到電鏟工作裝置的Adams動力學模型中，使用Simulink生成貼近實際的提升和推壓位移曲線以及挖掘阻力曲線，然后進行Adams?Simulink聯合動態仿真。最大提升力理論結果與仿真結果的相對誤差為-6.67%，最大推壓力理論結果與仿真結果的相對誤差為-5.94%，證實理論計算結果可作為基本設計的參考，克服傳統計算只取個別位姿的不足，為后續設計提供依據。該方法也可用于其他同類產品，尤其是采礦相關設備的分析。

參考文獻：

[1] WANG X B， SUN W， LI E Y， et al. Energy?minimum optimization of intelligent excavating process for large cable shovel through trajectory planning[J]. Structural and Multidisciplinary Optimization， 2018， 58（5）： 2219?2237. DOI： 10.1007/s00158?018?2011?6.

[2]?AWUAH?OFFEI K， FRIMPONG S. Cable shovel digging optimization for energy efficiency[J]. Mechanism and Machine Theory， 2007， 42（8）： 995?1006. DOI： 10.1016/j.mechmachtheory.2006.07.008.

[3]?李奎賢， 宋桂秋， 彭武良， 等. 挖掘過程及機械參數優化設計[J]. 東北大學學報（自然科學版）， 2001， 22（3）： 271?274. DOI： 10.3321/j.issn：1005?3026.2001.03.010.

[4]?鄒偉， 李奎賢， 周航， 等. 電鏟工作裝置機構優化設計的研究[J]. 采礦技術， 2015（1）： 70?71.

[5]?闞敏. 機械式挖掘機工作裝置動力學研究[D]. 沈陽： 東北大學， 2012： 32?61.

[6]?李奎賢， 王新中， 鄒宜民. 合理挖掘軌跡的確定及意義[J]. 礦山機械， 2000， 28（8）： 14?15.

[7]?林貴瑜， 李愛峰， 李奎賢. 確定挖掘阻力關鍵因素值與方法的研究[J]. 東北大學學報（自然科學版）， 2010， 31（12）： 1761?1764. DOI： 10.3969/j.issn.1005?3026.2010.12.023.

[8]?方自強， 胡國明， 李婉婉， 等. 挖掘機鏟斗挖掘過程的DEM仿真分析[J]. 工程機械， 2016， 47（3）： 43?51. DOI： 10.3969/j.issn.1000?1212.2016.03.008.

[9]?邢歡歡. 基于離散單元法的機械式挖掘機工作阻力模擬[D]. 沈陽： 東北大學， 2014： 16??42.

[10]?韓鵬. 基于Adams和MATLAB的挖掘機工作裝置動力學仿真[J]. 礦山機械， 2014， 42（10）： 35?38. DOI： 10.16816/j.cnki.ksjx.2014.10.008.

[11]?李鳳岐. 露天煤礦剝離爆破巖石粒度分布狀態[J]. 煤礦設計， 1994（8）： 10?13.

（編輯?武曉英）