基于Z′參數的高強鋁合金穩態蠕變速率可靠性研究

李 昂，高 蔚，吳 福，張 毅

(1.核工業理化工程研究院，天津 300180；2.國防科技工業核材料技術創新中心，天津 300180)

新型高強鋁合金是一類在7075合金基礎上Zn/Mg合金元素比更高的7系鋁合金。該類鋁合金具有高比強度、較高斷裂韌性、良好導熱性、耐特殊介質腐蝕等優點[1]，因此成為航空航天、船舶重工、核工業等領域主要的結構材料之一。

在溫度和應力的共同作用下，新型鋁合金材料的微觀組織及耐溫性能可能會發生緩慢變化。工程實踐表明，材料的蠕變變形斷裂是長期服役條件下壓力容器失效的主要形式之一[2-3]。因此，明確服役條件對材料蠕變性能的影響趨勢，對于機械設備部件的可靠性設計有著重要的研究意義。

前期的研究[4-5]提出，采用速率溫度參數(rate-temperature parameter, RTP)擬合各蠕變溫度和應力下的材料穩態蠕變速率數據，并通過應力σ-RTP主曲線外推得到其他條件下的蠕變性能。但新型鋁合金材料的穩態蠕變速率數據存在明顯的分散性，這可能是因為材料組織成分、制造工藝、實驗條件等因素的差異性造成的[6]。如何利用存在分散性的數據合理評估材料的蠕變性能，是新型高強鋁合金可靠性分析中必須回答的問題。相關文獻[7-10]表明，采用Z參數的評估方法可成功預測在一定可靠度下多種材料的持久壽命。但基于Z參數思想的評估方法在材料穩態蠕變速率預測方面的應用還鮮有報道。

本文結合新型高強鋁合金的穩態蠕變速率數據，利用改進后的Z′參數對鋁合金的穩態蠕變速率數據進行分析，研究Z′參數的統計分布特征。考慮材料數據的分散性，建立基于Z′參數的材料穩態蠕變速率預測方法及可靠性分析方法，為新型高強鋁合金蠕變性能可靠性評估及部件優化設計提供理論方法和數據支持。

1 改進的Z′參數模型

在壽命預測方法中，傳統Z參數表示了材料持久性能數據偏離σ-時間溫度參數(TTP)主曲線的程度。因此Z參數的分布可表征持久性能的數據分散性，進而實現持久壽命的可靠性分析。Z參數可表示為：

Z=TTP-Z0-Z1lgσ-Z2lg2σ-

Z3lg3σ-…-Znlgnσ

(1)

式中：σ為實驗應力；Z0～Zn均為常數。從式(1)可看出，選擇合適的時間溫度參數和應力之間的函數關系式是準確推算壽命的關鍵。

為研究材料穩態蠕變速率數據的分散性及可靠性，根據前期研究[4-5]提出的RTP RMB′模型修正Z參數的表達式，而應力函數P(σ)選擇文獻[6]中推薦的四階對數應力多項式。改進后的主曲線表達式及Z′參數模型如下：

a2lg2σ+a3lg3σ+a4lg4σ

(2)

a2lg2σ-a3lg3σ-a4lg4σ

(3)

2 新型高強鋁合金穩態蠕變速率數據的分布規律

蠕變實驗所用的新型高強鋁合金由北京航空材料研究院提供。材料的熱處理狀態為T6態。參考國標[11]，沿預鍛坯的徑向方向加工φ5 mm標準棒狀蠕變試樣。在40、60、80、100 ℃的蠕變實驗中，共獲得有效的穩態蠕變速率數據41個，數據分布情況如圖1所示。

根據以上的穩態蠕變速率數據，利用多元線性回歸法計算得到了新型高強鋁合金的σ-RTP的主曲線，如圖2所示。蠕變實驗數據與主曲線預測數據的對數殘差平方和的均值為0.034 81。從圖2中分布趨勢可看出，雖然蠕變數據取自不同的溫度實驗，但實驗數據交錯重疊地分布在σ-RMB′的關系曲線周圍，并未出現明顯的偏離現象。根據式(3)，Z′參數表征蠕變數據偏離主曲線的程度，其表達式中的參數擬合值列于表1。

圖1 新型高強鋁合金穩態蠕變數據的分布Fig.1 Distribution of steady creep data of new high strength aluminum alloy

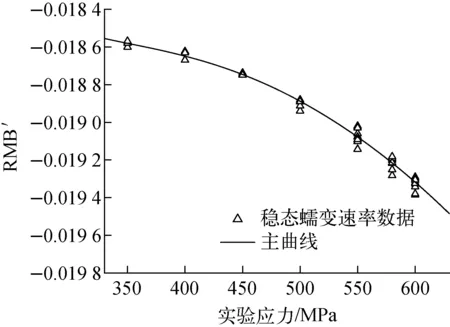
圖2 新型高強鋁合金的蠕變數據分布與主曲線Fig.2 Experimental creep data and master curve for new high strength aluminum alloy

表1 Z′參數表達式的參數擬合值Table 1 Optimized parameters in Z′-parameter equation

R(Z′)=1-F(Z′)=

(4)

3 新型高強鋁合金穩態蠕變速率的可靠性分析

在確定新型高強鋁合金穩態蠕變速率的分布規律后，結合可靠度的概念，對穩態蠕變速率數據進行分析。通過式(4)建立不同可靠度下新型高強鋁合金σ-RTP-R曲線，如圖3所示。圖3中R分別為50%、95%、99.7%(3s)。從圖中可清楚地看出，絕大多數的蠕變數據分布在可靠度為50%的預測曲線兩側，而所有的數據均分布在可靠度為3s預測曲線的右上區域內。以上現象說明可采用Z′參數法對新型高強鋁合金的穩態蠕變速率進行分析及預測。

圖3 新型高強鋁合金的蠕變數據與σ-RTP-R曲線Fig.3 Creep rate data and σ-RTP-R curves for new high strength aluminum alloy

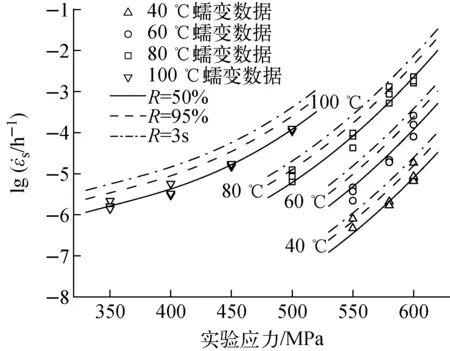
圖4 新型高強鋁合金的曲線的評價結果Fig.4 Evaluated results of curves for new high strength aluminum alloy

圖5為不同服役條件下新型高強鋁合金材料可靠度隨外推穩態蠕變速率的變化趨勢。對比不同服役條件下的曲線，隨溫度水平或應力水平的增加，材料可靠度曲線沿外推穩態蠕變速率增加的方向發生偏移，可靠度50%條件下的穩態蠕變速率上限逐漸升高，這與圖4反映的規律較為一致。該現象表明在一定的可靠度下，溫度和應力的變化可顯著影響新型高強鋁合金穩態蠕變速率的預測上限。根據圖5中的計算數據，在40 ℃、640 MPa的服役條件下，可靠度95%、3s對應的外推穩態蠕變速率上限分別為3.020×10-4、4.764×10-4h-1。在60 ℃、620 MPa的服役條件下，相應可靠度的外推穩態蠕變速率上限分別為1.000×10-3、1.700×10-3h-1。

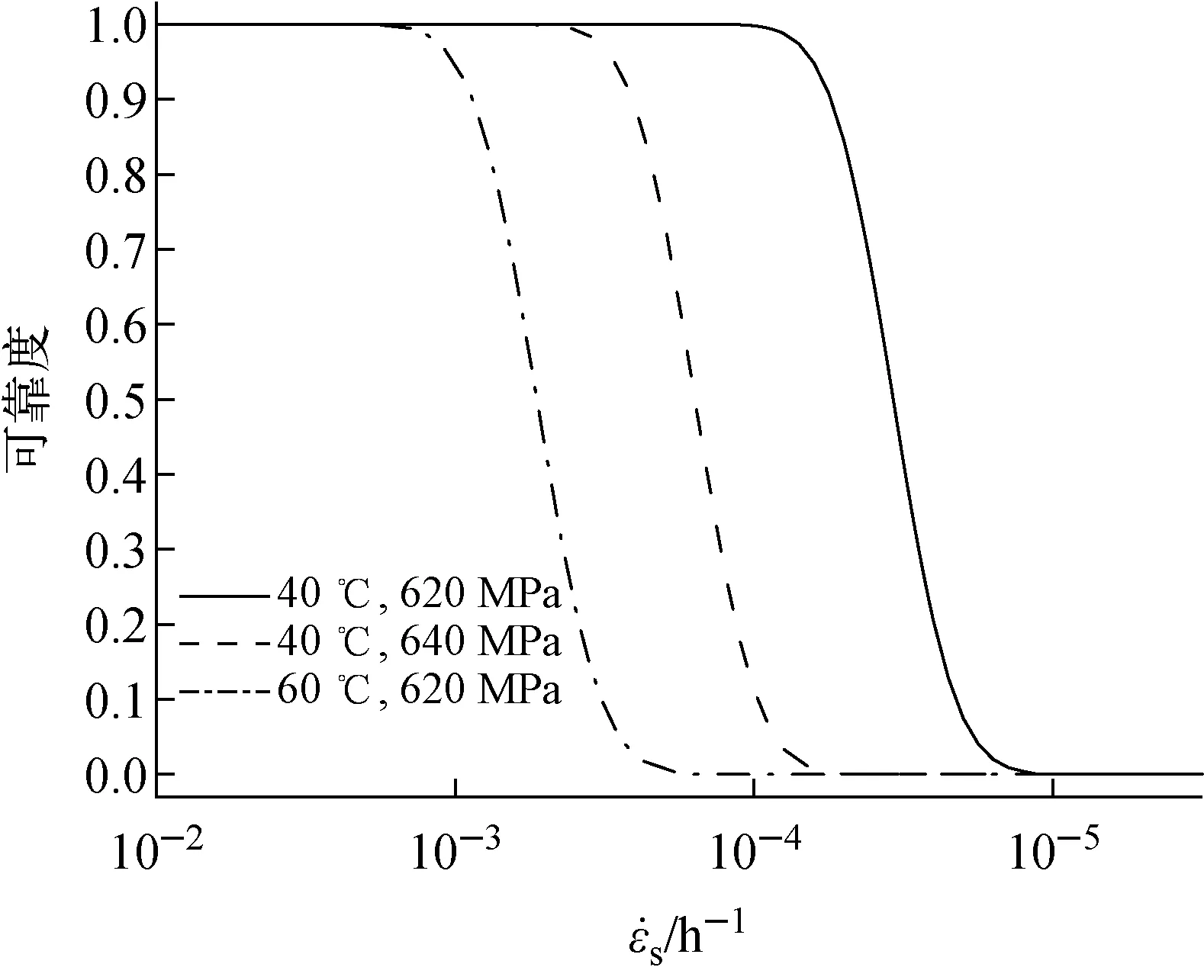
圖5 不同服役條件下材料穩態蠕變速率 上限與可靠度的關系曲線 curves for new high strength aluminum alloy under different service conditions

為檢驗預測曲線評估結果的準確性，開展了不同蠕變條件下的驗證實驗，實測數據與預測結果列于表2。對比表2中數據可知，雖然新型高強鋁合金的蠕變數據具有明顯的分散性，但驗證實驗的實測數據均未超過3s可靠度曲線預測的穩態蠕變速率上限。因此，當評估部件的長期穩定性時，建議選擇3s可靠度曲線來計算材料的蠕變性能及許用應力。

4 基于Z′參數的許用應力評估

由于蠕變試樣狀態(材料熔煉、熱處理狀態、加工精度等)存在著一些無法預知的差異因素，新型高強鋁合金的蠕變數據存在明顯的分散性。在工程設計[15]中，常以安全系數法來解決由材料、試樣不確定因素造成的數據分散性問題，但安全系數的選取完全依賴于設計者的設計經驗及部件的關鍵程度，并不考慮數據的實際分散性。

表2 新型高強鋁合金穩態蠕變速率的可靠性預測Table 2 Reliability prediction of steady creep rate for new high strength aluminum alloy

圖6 新型高強鋁合金在10-7 h-1下[σ]-T-R曲線 與安全系數法[σ]-T-K曲線的對比Fig.6 Evaluated results of [σ]-T-R curves and [σ]-T-K curves in 10-7 h-1 for new high strength aluminum alloy

基于Z′參數的分布特征，計算確定了外推至指定穩態蠕變速率條件下新型高強鋁合金的許用應力[σ]-T-R曲線。圖6為材料外推至10-7h-1下的[σ]-T-R曲線。采用傳統安全系數法，根據主曲線計算得到了安全系數K分別為1.1、1.2時的[σ]-T曲線，同樣標示在圖6中。根據圖6中的計算數據，新型高強鋁合金在50、80 ℃下的許用應力(可靠度3s)分別為470.0、294.5 MPa。從外推至指定穩態蠕變速率上限值的[σ]-T-R曲線中可發現，當可靠性越高時，相應服役溫度下的許用應力[σ]越小。對比基于Z′參數的[σ]-T-R曲線和傳統安全系數法的[σ]-T-K曲線，K=1.1的曲線的大部分處于95%可靠度許用應力曲線的下方，但與3s可靠度預測曲線發生了明顯的交叉，說明K=1.1的評估結果并不能完全保證可靠度達到3s。在70 ℃以下的溫度區域，K=1.2的評估曲線均位于3s可靠度許用應力曲線的下方，且隨著溫度的降低，兩種預測方法計算得到許用應力的差值逐漸增大。這說明在近常溫區域的材料許用應力評估中，傳統安全系數法無法充分發揮材料的耐溫性能，不利于提高機械設備及部件的經濟性。從以上的討論可知，傳統安全系數法無法兼顧材料的安全性及經濟性。相比而言，基于Z′參數的可靠性分析方法可充分考慮材料實測數據的分散性，結合可靠度的預測結果更合理。

5 結論

1) 以Z′參數作為狀態參量描述材料穩態蠕變速率的分散性，建立了基于RMB′模型的新型高強鋁合金Z′參數表達式。

2) 采用Shapiro-Wilk檢驗法對新型高強鋁合金Z′參數分布進行統計檢驗，結果表明在顯著性水平0.05的條件下，新型高強鋁合金的Z′參數分布服從正態分布規律且不存在異常值。采用極大似然估計法，計算確定了材料的累積失效概率函數：

(5)

3) 根據Z′參數的可靠性分析結果，建立了新型高強鋁合金的σ-RTP-R曲線和[σ]-T-R曲線。經計算，外推至穩態蠕變速率上限10-7h-1，新型高強鋁合金在50、80 ℃下的許用應力(可靠度3s)分別為470.0、294.5 MPa。

4) 與傳統安全系數法相比，基于Z′參數的可靠性評估法可考慮材料蠕變數據的實際分散性，兼顧材料的安全性與經濟性，結合可靠度得出的預測結果更為合理。