圖上算術結構的電阻距離矩陣

，，

（湖南師范大學 數(shù)學系，湖南 長沙 410081）

1 背景知識

對于一個簡單圖G=(V,E)，若列向量對，則稱(d,r)為圖G的算術結構，如果滿足：

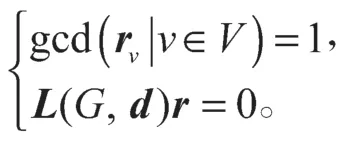
注意：列向量d和r的所有分量都是正整數(shù)，且d和r相互確定。(G,d,r)叫做算術圖，L(G，d)是其算術結構的拉普拉斯矩陣。任何圖G都有拉普拉斯算術結構，即(d,r)=(degG,1)，d=degG表示圖G的度向量，r=1為全是1的列向量。

令矩陣BT表示矩陣B的轉置，A是一個m×n的矩陣，n×m的矩陣G被稱為是A的廣義逆，如果滿足AGA=A。

一個n×m的矩陣G被稱為是A的Moore-Penrose逆，如果滿足以下條件：

i）AGA=A；

ii）GAG=G；

iii）(AG)T=AG；

iv）(GA)T=GA。

我們用A+表示A的Moore-Penrose逆。

圖的算術結構的概念，是D.J.Lorenzini[1]研究代數(shù)幾何中退化曲線時出現(xiàn)交矩陣而引入，更多可參見文獻[2]中的幾何觀點。其后，關于算術結構的研究，吸引了很多學者，如在文獻[1]證明了簡單連通圖上的算術結構個數(shù)是有限的；文獻[3]研究了路和圈上的算術結構個數(shù)的精確值等。

圖距離的研究在圖論中是非常重要的內(nèi)容之一[4-9]。電阻距離是圖的距離，在圖的隨機游動、網(wǎng)絡連通性、物理學等各個領域都有研究，如文獻[4]和文獻[5]。本文在R.B.Bapat的文獻[6]和[7]的研究基礎上，將一般連通圖G上的電阻距離和電阻距離矩陣擴展到算術圖上。首先，利用算術結構的拉普拉斯矩陣定義一個算術結構的電阻距離ρ(i,j)，再用圖的算術結構的電阻距離ρ(i,j)表示矩陣中位置元素(i,j)，得到其算術結構的電阻距離矩陣H，并最終求出它的逆矩陣。

2 算術結構的電阻距離

首先，回顧一下經(jīng)典距離滿足的公理：

令G是一個頂點集為V(G)={1,2,…,n}的連通圖，且令d∶V(G)×V(G)→R，如果d表示兩個頂點之間的一個度量，那么d應該滿足如下條件：