透視分步突破,深度變式探究
王雷 葛艷

[摘? 要] 函數綜合題是中考數學的重點題型,其中不僅包含眾多的函數曲線,同時涉及一些關鍵的知識聯系點,因此可以充分考查學生的知識能力. 解析問題時,需充分挖掘問題本質,從知識聯系性出發選取合適的方法,文章以一道函數綜合題為例,進行分步突破,解后思考,并提出相應的教學建議.
[關鍵詞] 一次函數;反比例函數;線段;點坐標
考題呈現
試題(2019江蘇泰州中考)已知一次函數y1=kx+n(n<0)和反比例函數y2=■(m>0,x>0).
(1)如圖1,若n=-2,且函數y1,y2的圖像都經過點A(3,4).
①試求m和k的值;
②請直接寫出當y1>y2時x的取值范圍.
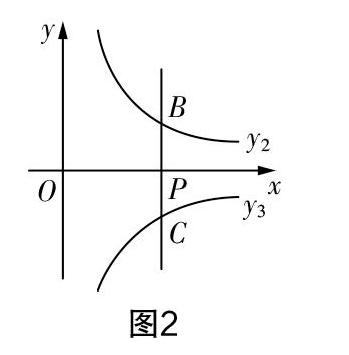
(2)如圖2,過點P(1,0)作y軸的平行線l與函數y2的圖像交于點B,與反比例函數y3=■(x>0)的圖像交于點C.
①若k=2,直線l與函數y1的圖像交于點D,當點B,C,D中的一點到另外兩點的距離相等時,試求m-n的值;
②過點B作x軸的平行線,與函數y1的圖像交于點E,當m-n的值為不大于1的任意實數時,點B,C之間的距離與點B,E之間的距離之和d始終是一個定值,求此時k的值及定值d.
分步突破
上述考題是中考常見的函數綜合題,以一次函數與反比例函數為命題背景,涉及求函數解析式、取值范圍和距離分析,以及定值求解等,由于考題有兩問,每一問又細分為兩小問,均含有各自的主干信息,所以下面對其分步突破.
1. 第一步:解構函數,巧定范圍
題干給出了一次函數y1和反比例函數y2的解析式,對于第(1)問,設定n的值為-2,并給出了兩函數的交點,所以第①問求函數解析式可以采用待定系數法,直接將點的坐標代入函數解析式即可. 將點A(3,4)代入一次函數解析式y1=kx-2中,可解得k=2. 將點A的坐標代入反比例函數解析式y2=■中,可解得m=12,所以m的值為12,k的值為2.
第②問分析y1>y2時x的取值范圍,屬于函數背景下的代數分析. 對于條件“y1>y2”,在函數圖像中的表現為一次函數位于反比例函數圖像的上方,因此問題轉化為分析一次函數位于反比例函數圖像上方時對應的x的取值范圍. 而點A是兩函數圖像的交點,是其分界線,顯然點A的右側部分滿足要求,又點A的橫坐標為3,因此當y1>y2時,x的取值范圍為x>3.
2. 第二步:分類討論,定值變形
第(2)問中添加了反比例函數y3,通過作y軸的平行線產生了交點B和C. 第①問中設定點D是直線l與函數y1的交點,于是可求得點D的坐標為(1,2+n). 根據l與函數y2,y3之間的交點可求得B,C的坐標,即B(1,m),C(1,n). 點B和點C位于x軸的兩側,根據題干要求,實際上就是分析其中的中點情形,顯然有三種情形:情形一是點D是BC的中點,情形二是點B是DC的中點,情形三是點C是BD的中點. 需要對其進行分類討論,且線段長就是兩點的縱坐標的差的絕對值.
情形一,當點D是BC的中點時,有BD=CD. 又BD=m-(2+n),CD=2,所以m-(2+n)=2,即m-n=4. 滿足限制條件,所以該情形存在,此時m-n=4.
情形二,當點B是DC的中點時,有DB=BC. 又DB=2+n-m,BC=m-n,所以2+n-m=m-n,解得m-n=1. 滿足限制條件,所以該情形存在,此時m-n=1.
情形三,當點C是BD的中點時,有BC=CD. 因為BC=m-n,CD=n-(2+n)=
-2<0,不可能,所以點C不可能是BD的中點.
綜上可知,對于第(2)①問,m-n的值為4或1.
第②小問設定點E是過點B的平行于x軸的直線與直線y1的交點,所以點E的坐標為■,m. 根據定值構建的思路可知,d=BC+BE,只需要將所涉及的點的坐標代入其中即可. 當點E在點B左側時,有d=m-n+1-■,分析該式為定值時d和k的值,只需對式子進行變形,將其中的參數以乘積形式表現即可,于是d=(m-n)1-■+1,所以當1-■=0時,顯然d的取值與m,n無關,此時k=1,d=1. 當點E在點B的右側時,有d=m-n+■-1,分析該式為定值時d和k的值,只需對式子進行變形,將其中的參數以乘積形式表現即可,于是d=(m-n)1+■-1,所以當1+■=0時,顯然d的取值與m,n無關,此時k=-1,d=-1,矛盾,說明此種情形不存在. 綜上可知,對于第(2)②問,k=1,d=1.
解后反思
上述是對考題的解析突破過程,考題考查了求函數解析式、取值確定和分析線段長,涉及一次函數、反比例函數的基礎知識,以及圖像中交點的求解方法,下面對突破過程進行深入反思.
1. 解析中的關鍵步驟
考題分為兩大問,無論是求取值,還是分析距離關系,均需要準確把握函數圖像的位置關系,明晰函數的交點. 而對于每一小問,還需要把握其中的關鍵步驟,如第(1)②問在分析y1>y2時x的取值時,需要理解不等式與函數圖像之間的聯系,即y1>y2不僅表示大小關系,在函數中還體現為圖像的上下關系,基于該內容就可以直接獲得突破方法. 又如第(2)①問分析三點之間的距離相等關系,其關鍵步驟是結合限制條件對三點之間的位置關系進行討論,并結合點坐標進行細化,這也是函數背景下線段長與點坐標關系構建的方法. 第(2)②問中的含參數的代數式的定值討論,解析的關鍵步驟是對代數式進行變形,即實現參數部分的因式分解,從而可通過設零將其消去.
2. 值得學習的內容
中考壓軸題的學習價值在于,可以從中提煉出問題突破的思路和方法,從而掌握同類題的突破方法. 以第(1)②問為例,求“y1>y2時x的取值范圍”,其解析本質就是數形結合,同時可以提煉出不等式問題的轉化方法——圖像分析法. 而對于第(2)問,實際上均可以歸結為函數背景下的線段長分析. 從解析過程可知,利用點坐標來描述線段長是問題突破的核心,這也是函數與幾何之間的知識聯系點. 因此,求解與幾何相聯系的函數綜合題時,要充分把握“點坐標”這一中間媒介,實現幾何問題的代數轉化.
3. 關于考題的變式
開展考題變式不僅可以深化問題認識,還可以拓展學生的解題思維,下面是以本考題所涉及的兩個核心價值內容展開的變式探究.
變式1 (基于不等式圖像解析方法進行變式)已知點A(3,b)是一次函數y1=kx+n與反比例函數y2=■(m>0,x>0)在第一象限的交點,若不等式kx+n>■的解為x>3,試分析k的正負.
思路點撥 由不等式的解可知,當0
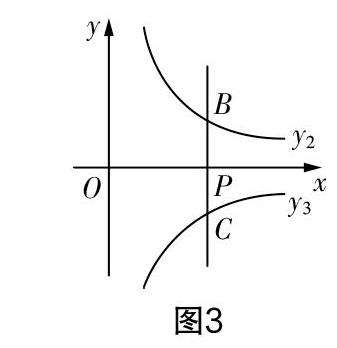
變式2(基于函數與幾何的聯系點進行變式)已知反比例函數y2=■(x>0),一次函數y1=-2x-2,如圖3,過點P(1,0)作y軸的平行線l與函數y2的圖像交于點B,與反比例函數y3=-■(x>0)的圖像交于點C. 試分析在函數y1上是否存在一點D,使得∠BDC=90°. 若不存在,請說明理由;若存在,請求出點D的坐標.
思路點撥根據題干信息可求出B(1,12),C(1,-2),可將點D的坐標設為(a,-2a-2),在Rt△BCD中使用勾股定理可得BC2=BD2+CD2,然后利用點坐標可以分別求出線段長,基于線段長關系即可構建相應的代數方程,即可分析a是否有解.
■ 教學建議
1. 關注函數綜合,解構曲線圖像
函數綜合題是中考的核心考題,一般因綜合性強而解析難度大,實際上可以將函數綜合看作是多條曲線之間的綜合,因此解題時就可以通過分析曲線之間的聯系點來加以突破. 而在日常教學中,需要教師對初中階段所涉及的函數曲線進行系統歸納,包括一次函數、二次函數和反比例函數,讓學生對函數的曲線特征、性質結構有一個充分的了解,能夠根據函數解析式準確畫出相應的圖像,并能根據曲線之間的位置關系得出特征參數的值. 例如根據函數y1=kx+n(n<0)與反比例函數y2=■(m>0,x>0)相交可以得出k>0. 建立函數之間的圖像聯系是求解綜合題的關鍵,也是數形結合策略分析問題的基礎.
2. 重視突破方法,形成解題思路
綜合題的突破除了需要具備扎實的基礎知識外,還需要掌握相應的解析方法. 例如上述求解函數解析式所采用的待定系數法,分析距離問題時所采用的分類討論和線段坐標化方法,正是在這些方法的靈活使用下才促使問題得到了解決. 因此,教學中需要教師對考題的解析方法加以總結提煉,讓學生掌握根據考題特征選取合適方法的思路. 對于一些結構鮮明的考題,更應注重總結. 例如函數與幾何綜合題,應讓學生把握函數與幾何之間的聯系點——點坐標,形成“函數解析式?圳點坐標?圳幾何特征”的突破策略.
3. 注重考題變式,拓展數學思維
中考壓軸題的問題形式多樣,圖像變化也十分靈活,所以開展考題教學時不能拘泥于問題本身,而應引導學生對背后的實質內容進行挖掘,并結合相關知識對其中的核心內容開展變式探究. 例如上述基于聯系點對考題進行了不等式轉化變式和幾何特征變式,可使學生充分認識到函數圖像與不等式、幾何之間的關聯. 而在變式探究過程中,則需要掌握適度原則,不能因變式不足使得探究無意義,也不能因過度變式造成超綱超范圍的現象. 在變式探究的過程中,學生的數學思維可以得到鍛煉,能促進學生創新思維的形成.

