復習課堂中的生長數學

朱鳴

[摘? 要] 在八年級上學期期末復習教學中，將軸對稱、二次根式、一次函數等相關內容一網打盡，充分挖掘其中所蘊含的數學思想方法，借助數形結合的“原動力”、分類討論的“生長節”、假設方程的“選擇器”，作為后續課堂“生長數學”教學的開端，使數學知識和方法在此生根發芽，茁壯成長.

[關鍵詞] 生長數學;復習課堂;勾股定理

生長數學下的價值判斷

1.？搖授課對象

本節內容授課對象為某實驗初中八年級平行班學生.

2.搖教材分析

所用教材為蘇科版《義務教育教科書·數學 》（八年級上冊）. 教學內容為 “勾股定理”“勾股定理的逆定理”“勾股定理的簡單應用”等相關課程. 如果期末復習只拘泥于以上內容，在這個框框內翻轉騰挪，那培養學生創新意識和實踐能力的效果不免要打折扣.

3.搖學情分析

學期已步入尾聲，學生較系統地學習了“軸對稱圖形”“勾股定理”“實數”“平面直角坐標系”“一次函數”等相關知識，學生對于以上各獨立的知識或許掌握尚可，但若通過某一堂課或緊密相連的幾節課將八年級上冊所學知識較系統、有邏輯地加以綜合，學生會倍感吃力. 基于上述的教材觀、學生觀、教學觀，可以確定下列教學目標及教學重難點.

4.搖目標要求

教學目標：

①了解勾股定理的代數表示和幾何意義，能夠靈活運用勾股定理解決一些問題.

②通過具體問題，進一步掌握數形結合、分類、方程等數學思想方法，發展合情推理和演繹推理能力.

③回顧本章所學知識和方法，對本章知識進行梳理，使所學知識系統化、結構化，進一步積累數學活動經驗.

教學重點：數形結合視角下的勾股定理應用.

教學難點：建構章節知識體系，初步感受在分類思想下使用方程研究問題的一般科學方法.

價值判斷下的活動設計

1. 建構知識網絡

教師：學期步入尾聲，今天這節課，老師想和同學們復習一下“勾股定理”的相關內容（板書課題：勾股定理復習）. 在開始前，我們不妨先熱身一下.

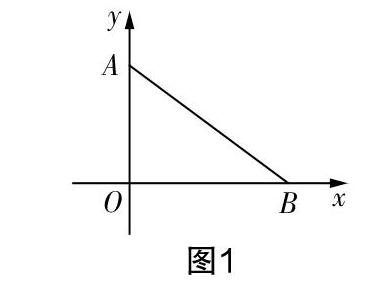
問題1：已知，如圖1，直線解析式y=-■x+6 與x軸、y軸分別交于點B、點A.

教師：請直接說出A，B的坐標.

學生1：A（0，6）， B（8，0）.

教師：請計算一下A，B兩點之間的距離.

學生2：AB=10，由圖形中的直角三角形出發，利用勾股定理，直接計算斜邊長.

教師：學生2回答的思路十分清晰，那還有其他方法可以求出AB兩點之間的距離嗎？

學生2：不知道了.

學生3：（舉手示意）兩點之間距離公式AB=■，代入即可.

教師：計算A，B兩點之間的距離，這個距離公式正是源自于勾股定理. 那如何計算點O到線段AB的距離呢？同學們可以花2分鐘時間，著手解決一下.

學生4：等積法，距離為■.

教師：學生4反應很快. 我們發現在初中階段，和兩點之間的距離相對照，點線之間的距離問題常使用等積計算來解決.

問題2：已知，如圖2，將點B沿平行于y軸的直線向上平移10個單位到C點，在x軸上找一點P，使AP與CP的距離之和最小.

教師：請各位拿出作圖工具，在活動單上找出點P，并求出此時的距離和，可以花5分鐘來解決問題.？搖（教師巡視，由于時間間隔較久，學生對于利用“小馬喝水”這類模型，結合期初“軸對稱”章節中的中垂線性質構造直角三角形，利用勾股定理來解決這個問題顯得較為生疏）

教師：好，時間到了，有誰能解決這個問題？

學生5：（上臺展示）這是一個“小馬喝水”問題，關鍵是找出對稱點，然后構造直角三角形，用勾股定理解決.

教師：學生5在幫大家回憶往昔，常規思路，常規操作！那你們能求出此時的P點坐標嗎？

學生6：可以使用“一次函數”來解決問題，由確定的兩點，解出直線解析式，然后求出其與x軸交點的坐標，就是P點的坐標了.

教師：學生6提供了一種我們現有水準可以解決問題的方法，十分不錯. 今后，隨著學習進程加深，此類問題還可以采用其他的方法來解決，例如“相似”.

教師：同學們，以上兩個問題有圖有真相，然后再使用代數的方式寫寫算算，如果我們將這兩者結合起來看，就是數學學習中的一種基本方法，你們覺得這種方法叫什么？

學生7：數形結合.

教師：（板書：數形結合）言簡意賅！

問題3：已知，如圖3，x軸上有一動點P，與點A，B構成一個三角形，若AB=10，AP=2■，BP邊上的高為6.

教師：請自行作圖，求出△ABP的面積.

學生8：（上臺展示，只展示了P點在O點右側的情況）？搖？搖？搖？搖？搖

學生9：還有，還有. （上臺展示， P點在O點左右兩側的情況都考慮了）

教師：這個問題蘊含什么數學思想？

學生（齊）：分類思想.

教師：典型的分類思想. （板書：分類思想）世間萬事不是非黑即白，我們在今后的生活和學習中要學會全方位、多角度地思考問題，分門別類，有條不紊地解決問題.

問題4：已知，如圖4，若點P是x軸上的一個動點，當P運動到∠OAB的平分線上時，求此時點P的坐標.

教師：又來一個求坐標的問題，能用先前的方法解決嗎？如果不行，該怎么辦？

教師：學生10，能解決嗎？

學生10：（搖頭）不會.

學生11：（搖頭）沒有思路.？搖？搖？搖？搖

教師：（提示）在問題陷入“絕境”時，你不妨假設已經找到了這點，在“軸對稱”這一章中，你們剛剛用過了“中垂線的性質”那還有什么性質呢？

學生12：角平分線性質.

教師：（微笑點頭）

學生13：（上臺展示）由角平分線性質知道OP與P到AB的距離相等，構造直角△PHB，利用勾股定理來解決問題.

教師：具體一點.

學生13：我是設OP為x，則BP=8-x，PH=x，BH=4.

教師：（轉向班內學生）能理解BH=4嗎？

學生13：就是10減去6嘛（向同學解釋）.

教師：至此問題解決了. 學生13，這是一種什么數學思想？

學生13：設x.

教師：設x一般是用來干什么的？高大上一點.

學生13：建立方程.

教師：很機靈！（板書：方程思想）一般來說，在著手解決與勾股定理緊密相連的問題時，上述三種思想方法經常出現，頻繁使用.

問題5：已知，如圖5，若點P是x軸上的一個動點，當P運動到一定位置，使△ABP成為一個等腰三角形，求此時點P的坐標.

教師：今天坐標求得真不少，請同學們對照前后，看一下此問題中P點坐標的求解是否和先前一樣？

學生14：好像和上一題類似，但又不盡相同，我覺得要分一下類吧.

教師：怎么分呢？

學生14：我有點忘了……

教師：沒事，哪位可以幫一下學生14？

學生15：分別以點A、點B、點P為頂點，在x軸構造等腰三角形，我來畫一下吧.

教師：這比空對空講要直觀和具體.

學生15：（邊畫邊講）先以點A為頂點，左側對稱就可以了，再以點B為頂點，左右兩邊都行的.

教師：大分類下小分類，套路深啊！

眾生：（笑）

學生15：再以點P為頂點，作高以后就回到第2個問題了.

教師：具體一點.

學生15：中垂線性質，當？搖AP=BP時，在直角△AOP中，可以使用勾股定理來處理.

教師：具體的數學思想是什么？

學生15：用方程思想來解決.

教師：一個問題，三種思想方法均有呈現.

……

2. 典型問題拓展

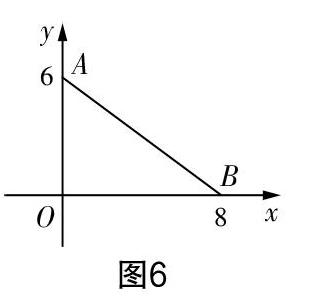
問題1：如圖6，若點P從原點開始沿x軸向右運動，速度為每秒一個單位，設運動時間為t，當t<8時，先畫出△ABP中AP邊上的高;當高為6時，求出垂足Q點的縱坐標.

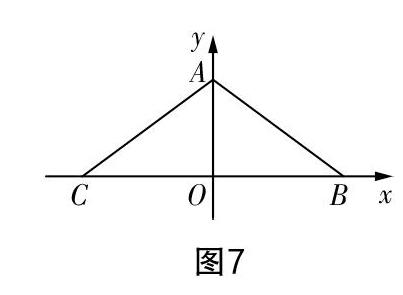
問題2：如圖7，在等腰三角形ABC中，底邊長16，腰長10，若點P沿x軸從點C開始向點B運動，速度為每秒一個單位，設點P的運動時間為t，請研究當t為何值時，點P和頂點A的連線與腰垂直？

3. 全課小結，布置作業（略）

活動設計下的教學思考

復習課容易上成新授課的再現，如同雞肋;復習課也容易上成習題課的翻版，味同嚼蠟. 但復習課的重要性不言而喻，尤其在期末復習階段. 課程標準中的“讓學生獲得良好的數學”“要教給學生有生長力的數學”“復習課也要為學生成長助力”等理念早已深入人心，那么，如何利用好復習課？如何通過復習相關內容，使課程綱舉目張，前后貫通呢？這是一個值得思索的問題. 而勾股定理作為初中數學中的一個重要定理，在八年級上學期期末復習教學中，完全可以依靠這個知識節點，將軸對稱、二次根式、一次函數等相關內容一網打盡，并且能充分挖掘其中所蘊含的數學思想方法，以此作為后續課堂“生長數學”教學的開端，使數學知識和方法在此生根發芽，茁壯成長.

1. 數形結合“原動力”

卜以樓教授將代數和幾何分別歸納為“式結構”和“形結構”的學科，其關注的焦點是代數中的數量關系和幾何中的位置關系的相互聯系和相互轉化. 以上面的問題為例，在幾個問題解決的過程中，我們發現，可以借助圖形，然后通過代數計算的方法進行研究，我們將其中蘊含的思想稱之為數形結合思想. 那么，初中數學中第一次出現數形結合的地方在哪里呢？答案很簡單，數軸就是學生第一次接觸到的圖形與數量的結合，只不過當時學生可能并不太在意. 隨著學習進程的深入，數量關系和位置關系結合的知識點不斷呈現，中點、角平分線、無理數、勾股定理等，乃至到數與形完美結合的工具——平面直角坐標系. 借助于這樣的工具，我們可以將距離公式（式結構），完美地利用勾股定理，展現成橫平豎直的直角三角形（形結構），實現數學學習的直觀化和簡約化，并能為今后高中數學中的平面向量和物理中的受力分析打下堅實的基礎. 小小距離，充滿著初生的“原動力”，向著未來生長.

2. 分類討論“生長節”

“數學是思維的體操”，我們知道數學可以訓練一個人的邏輯思維能力，而邏輯思維需要嚴密性和完備性. 那么，如何進行思維訓練呢？“從現代很多的認知心理學角度來說，分類的能力也是衡量嬰幼兒智力的一個標準. 所以，區分類別對于嬰幼兒的思維發展甚是重要. 無論對小孩長大之后的學習推理能力、辯論能力還是數學學習能力來說，從小掌握分類對這些的影響是很大的. 因此，在嬰幼兒早期教育階段如果讓孩子們學會正確分類，其實在一定的程度說是可以培養孩子的思維能力的. ”但是學生在幼兒期往往對人對事只能進行簡單分類，以孩童的視角看問題，非好即壞，非此即彼. 但我們知道萬事萬物并不像簡單的一枚硬幣只有正反兩面. 所以，初中數學學習，貫穿著分類的思想，并且是從簡單分類發展到復雜分類. 正如卜教授提出的“道是認識事物的方法論，術就是實踐過程中的方法”. 通過類似方法的浸潤，對照不同的標準，讓學生全方位、多角度地思索，實現 “以道馭術”. 從課堂中歷練的觀察、分析、解決問題的“生長節”，枝繁葉茂，可以繼續生長到情感、態度、價值觀的層次.

3. 假設方程“選擇器”

“學生的發展有兩種水平：一種是學生的現有水平，指獨立活動時所能達到的解決問題的能力，另一種是學生可能的發展水平，也就是通過教學所獲得的潛力，這兩者之間的差異就是最近發展區. ”對于問題5而言，學生能很自然地分別以點A，O，B為頂點構建等腰三角形，有直觀的相等，符合一般由簡到難的認知規律，契合學生發展的第一種水平. 而對于“線段垂直平分線的點到線段兩端距離相等”這個性質，雖然本課前面曾經出現過，但是仍然和問題4的“角平分線上的點到角兩邊距離相等”性質一樣，學生抓不住問題的本質. 在由“形結構”到“式結構”的轉換過程中，忽視了隱藏的相等. “方程是刻畫現實生活中相等關系的有效模型”，通過分析和引導，對于問題4中AB邊上的對稱點和問題5中x軸上的第4個P點，利用相等關系，構建直角三角形，然后使用勾股定理來求解，實現知識和方法的生長，同時使學生達到第二種水平. 事實上，分析方程思想，按照卜教授的觀點，其本質是一種假設思想，是一種嘗試的想法. 學生的選擇是一種試錯，既然無法一眼洞穿，那么可以用不同的假設去驗證它. 在種種備選方案中，選簡選優，進而加以決策，這也符合學生的認知規律，打通知識的聯系，培養學生的遷移生長能力.

“生長數學是前后一致的、邏輯連貫的、一以貫之的數學”，是充滿著“原動力”，布滿著“生長節”，鋪滿著“選擇器”的數學. 在復習課堂中，用全景式的構架來統領全局、縱覽前后，對知識和方法的生長大有裨益，進而可以推廣到其他類型的課程中，從而使每個學生茁壯成長！