壓電陶瓷驅動的長行程快刀伺服機構設計

閆 鵬，李金銀

(山東大學 機械工程學院 高效潔凈機械制造教育部重點實驗室，山東 濟南 250061)

1 引 言

近年來，具有自由曲面的光學元件及其他精密復雜器件在軍用、民用和空間探索等領域得到廣泛應用[1-2]。由于此類自由曲面元件特殊的表面結構和其多自由度的特點，使用較少的元件即可實現更高的光學效率，從而使得系統具有成本低、結構簡單、光學性能好、分辨率高等優點。然而光學自由曲面作為一種典型的非旋轉對稱曲面，具有不規則變化特征、沒有固定的回轉中心、形狀復雜且對加工精度的要求極高，傳統加工方法無法滿足此類零件的高效、高精密加工。在超精密加工技術中興起的快刀伺服技術(Fast Tool Servo，FTS)可以實現復雜曲面的高精度和高表面質量加工，具有高頻響、高定位精度的特點，成為加工復雜曲面元件的高效手段[3-5]。

快刀伺服系統一般采用壓電陶瓷[6-7]、音圈電機[8-9]、磁致伸縮驅動器[10]等作為驅動機構。與其他驅動器相比，壓電陶瓷驅動器具有高剛度、大輸出力、高分辨率的特點，能夠實現快刀伺服系統的高頻響和高精度加工性能，因此壓電陶瓷驅動的快刀伺服機構得到廣泛關注。然而，壓電陶瓷的輸出行程一般只有其自身長度的千分之一，傳統的壓電陶瓷型快刀伺服機構具有較高的固有頻率，但其輸出行程較小。Kim等[11]基于柔性鉸鏈機構，采用堆疊式壓電陶瓷驅動器設計了一種快刀伺服機構，用于補償加工過程中的主軸運動誤差。該快刀伺服機構運動分辨率0.15 μm，其運動行程只有數微米。Zhu等[12]采用壓電陶瓷驅動，實現了一種超高固有頻率的快刀伺服機構的設計和控制。得益于壓電陶瓷和柔性鉸鏈機構的使用，該機構具有5.35 kHz的超高固有頻率，從而使得系統能夠具有更高的帶寬和頻響性能，然而該系統行程也僅有數微米。壓電陶瓷驅動的快刀伺服機構行程小的缺點使得應用該技術加工某些復雜曲面時面臨困難，限制了快刀伺服技術的應用和發展。

為放大壓電陶瓷的輸出位移需要采用柔性放大機構，包括杠桿機構[13]、橋式機構[14]、Scott-Russell 機構[15]等。在這些柔性放大機構中，杠桿機構由于機構簡單、放大比穩定等特點在快刀伺服機構的設計中得到廣泛應用。Wang等[16]基于杠桿放大原則設計了柔性放大機構應用于快刀伺服系統，實現快刀伺服機構的長行程輸出。然而杠桿機構的非對稱性會產生寄生位移，影響曲面加工精度。為了補償杠桿放大機構產生的寄生位移，Liu[17]設計了一種長行程快刀伺服機構，該機構單獨設置一組驅動用以補償放大機構產生的寄生位移，然而該機構增加的驅動單元給機構的控制帶來挑戰，增加了系統的復雜度。

為實現壓電陶瓷驅動的快刀伺服機構的長行程輸出性能并消除機構的寄生位移，本文基于杠桿放大原則，設計和分析了一種壓電陶瓷驅動的長行程快刀伺服機構，并對該機構進行了有限元仿真和實驗驗證。有限元仿真和實驗結果表明，該機構能夠實現100 μm的長行程位移輸出，同時消除了寄生位移，能夠保證良好的加工精度。

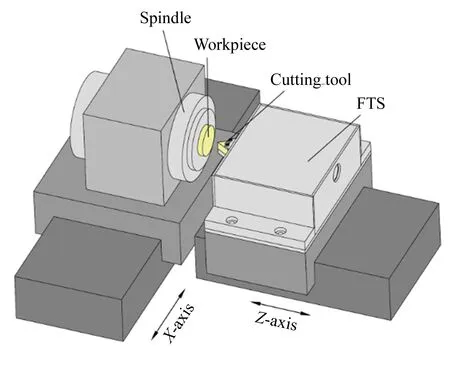
圖1 FTS加工原則Fig.1 Working principle of FTS

2 機械結構設計

快刀伺服整體加工系統如圖1所示，工件安裝在空氣主軸上，同時能夠在x方向移動，快刀伺服機構安裝在機床z軸的精密導軌上，金剛石刀具安裝在快刀伺服機構上。在加工過程中，工件隨主軸一同做旋轉運動，金剛石刀具在快刀伺服機構的帶動下，根據主軸旋轉信號進行相應的直線往復運動，從而去除工件表面材料，完成曲面加工。

本文設計的壓電陶瓷驅動的長行程快刀伺服機構如圖2所示。柔性機構具有無摩擦、無需裝配、結構緊湊的優點，可以實現壓電陶瓷輸出位移的放大和傳遞。在眾多類型的柔性鉸鏈中，直圓型柔性鉸鏈與一般柔性鉸鏈相比，旋轉精度更高，因此在設計中采用了直圓型柔性鉸鏈。

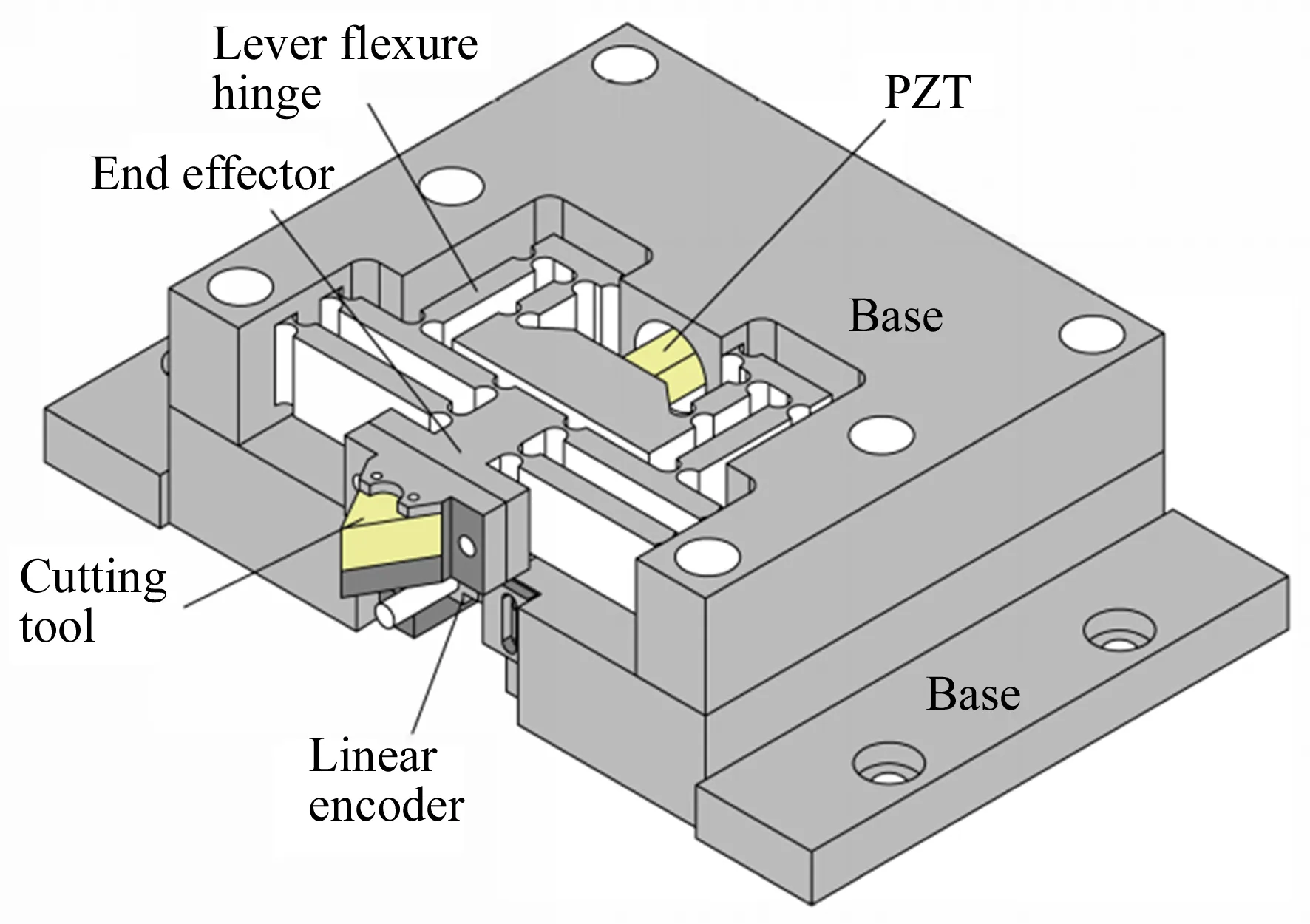
圖2 FTS機械結構Fig.2 Mechanical structure of designed FTS

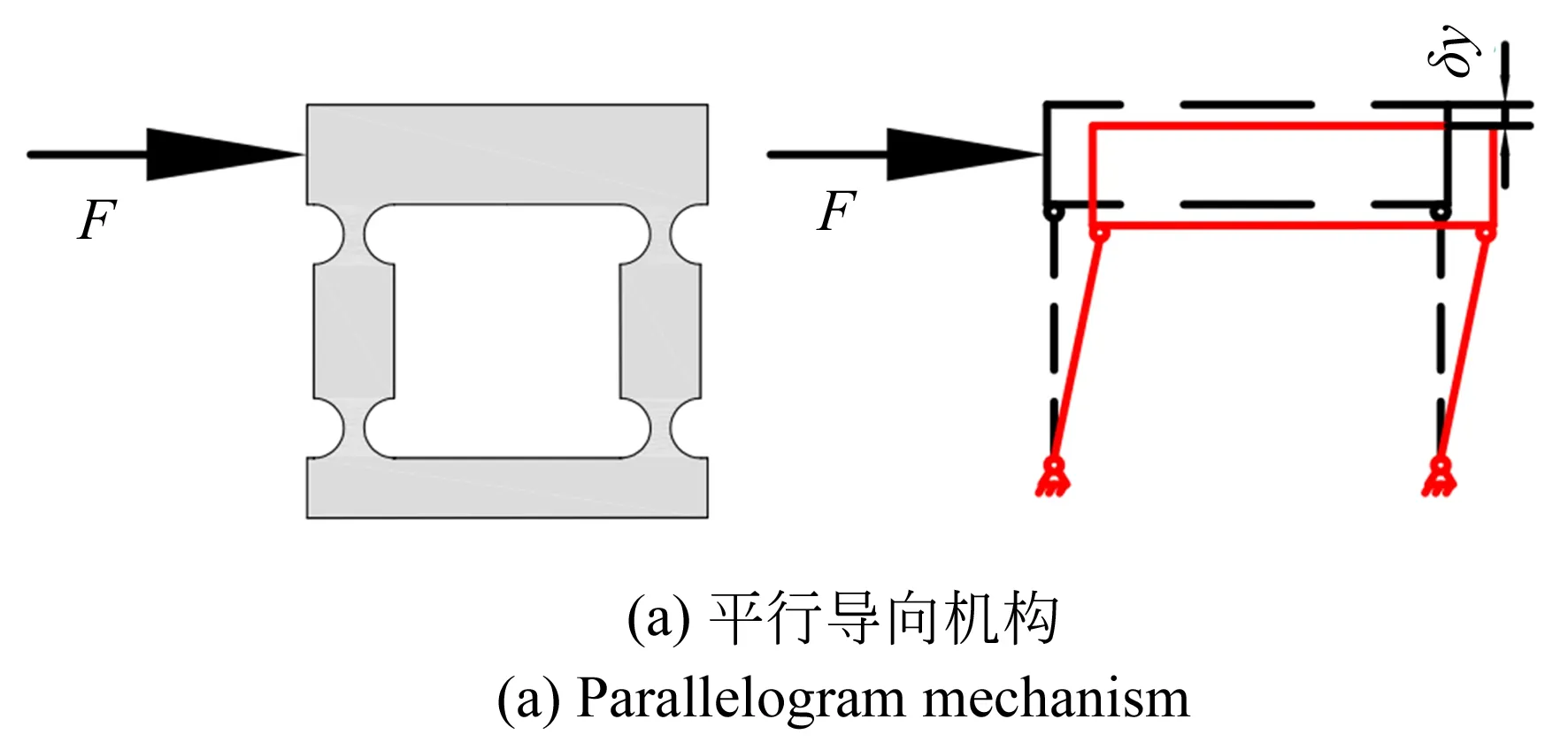
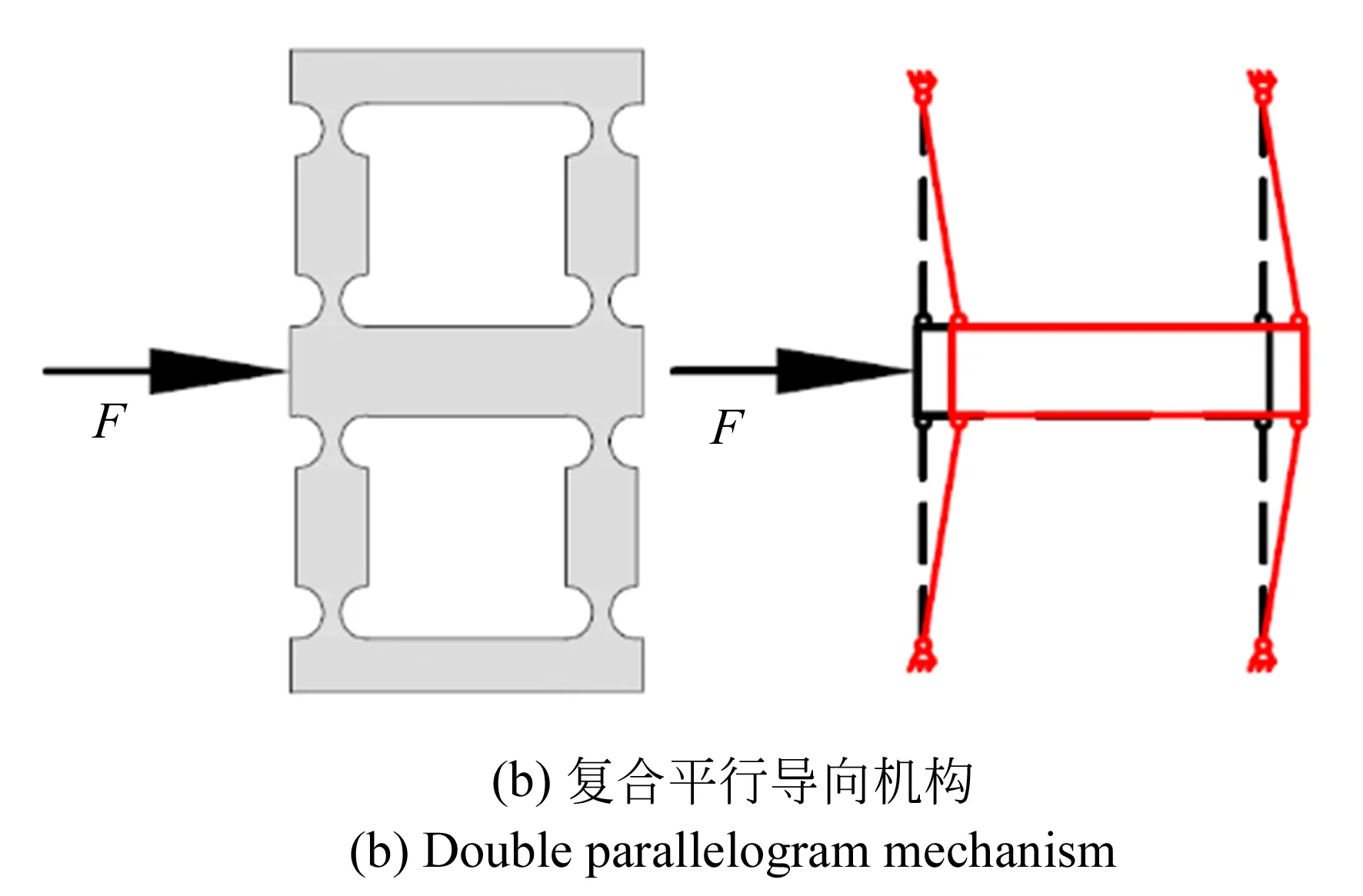
圖3 本文采用的復合平行導向機構Fig.3 Double parallelogram mechanism

在壓電陶瓷驅動的快刀伺服機構設計中，如何有效地抑制機構寄生位移的產生是提高系統加工精度的關鍵。如圖3所示，平行導向機構結構簡單，但在輸出指定位移的同時會產生一定的寄生位移。因此在設計時采用了復合平行導向機構，其對稱性結構能消除寄生位移，增加機構輸出端水平和垂直方向的剛度。

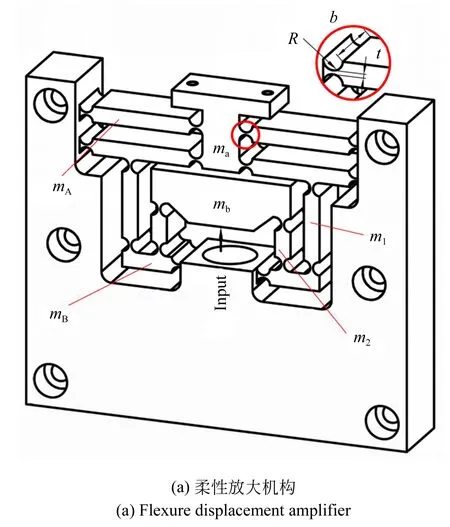
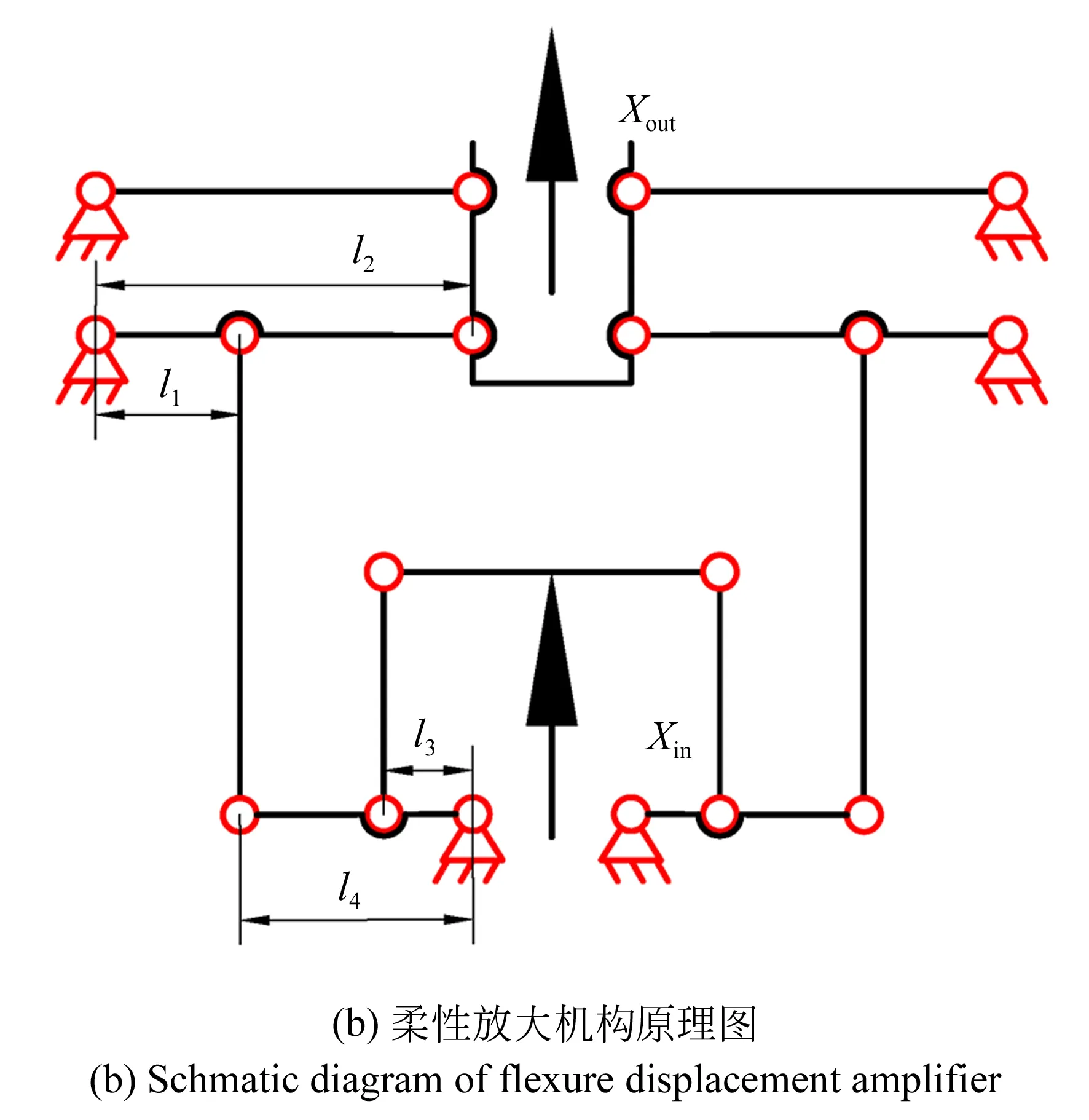
圖4 柔性放大機構及其原理Fig.4 Flexure displacement amplifier and its schmatic diagram

為實現快刀伺服機構的長行程輸出性能，需要采用柔性放大機構來放大壓電陶瓷驅動器的輸出位移。本文設計了一種對稱式的二級杠桿放大機構，如圖4所示。壓電陶瓷輸出位移，通過柔性放大機構進行放大，最終通過復合平行導向機構在末端運動平臺輸出位移。一方面，二級杠桿放大機構使得機構實現放大功能的同時結構更加緊湊，輸出端的放大杠桿也具有一定的導向作用，進一步精簡快刀伺服機構的機械結構。另一方面，整個放大機構采用對稱式結構，能夠在輸入端消除非工作方向的寄生位移，提高輸出精度。

3 理論建模和有限元仿真

3.1 機構動力學建模

根據偽剛體模型，本文設計的長行程快刀伺服機構可以等效為彈簧-質量-阻尼系統，如圖5所示。其中，Ke和Kpzt為柔性機構和壓電陶瓷的等效剛度，ce和cpzt是柔性機構和壓電陶瓷的等效阻尼系數，M是機構的等效質量，Fpzt是壓電陶瓷驅動力。

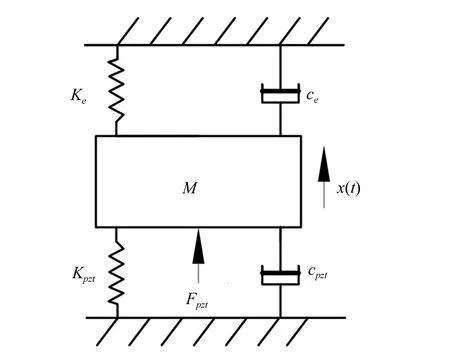
圖5 等效動力學模型Fig.5 Equival dynamic model

本文設計的長行程快刀伺服機構只在平面內運動，對于機構設計中采用的直圓鉸鏈，只考慮其在平面內的變形，基于柔度矩陣方法[18]，其輸出可簡化為:

(1)

式中：Δxi和Δyi分別為直圓鉸鏈在平面內沿x向和y向的形變，Δα為直圓鉸鏈繞z軸的轉動角度。假設直圓鉸鏈理想旋轉，即忽略直圓鉸鏈彈性變形下的位移，只考慮直圓鉸鏈的旋轉剛度，可得:

(2)

式中kR為直圓鉸鏈的旋轉剛度。

用拉格朗日原理分析機構的動力學模型，此機構的等效動能為:

(3)

式中：nA=4，nB=2，分別代表輸出端和輸入端連桿的數量，x代表輸出端位移，ma,mb代表輸出端和輸入端平臺質量，m1,m2代表次級放大和初級放大機構處連桿的質量，IA,IB分別代表輸出端和輸入端連桿的轉動慣量：

(4)

(5)

其中mA，mB分別代表次級放大和初級放大杠桿的質量，分別為：

mA=ρ(l2·b·(2R+t)-πR2b)，

(6)

mB=ρ((l4+3R+t/2)·b·(2R+t)-πR2b).

(7)

機構的彈性勢能為：

(8)

式中：n1=10，n2=8，分別代表輸出端和輸入端直圓鉸鏈個數，θ1，θ2分別代表輸出端和輸入端鉸鏈的旋轉角度：

(9)

(10)

忽略等效動力學模型中的阻尼影響，對設計的長行程快刀伺服機構應用拉格朗日方程可得：

(11)

系統的動力學方程為：

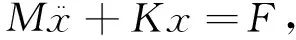
(12)

其中：

(13)

(14)

由此可得機構的固有頻率:

(15)

忽略壓電陶瓷預緊力對機構輸出行程的影響，機構的最大輸出位移為:

(16)

式中：Xn為壓電陶瓷的最大輸出行程，X為機構的最大輸出行程。

在上述分析中，機構的行程輸出隨著直圓鉸鏈的旋轉變形增大而增大。然而值得注意的是，隨著直圓鉸鏈的旋轉變形增大，變形應力也隨之增加，鉸鏈的變形應力會影響機構的使用可靠性。對于直圓鉸鏈，其最大應力和最大旋轉變形的關系[19]為：

(17)

式中:β=t/2R，f(β)為一無量綱因子:

(18)

3.2 參數設計和有限元仿真

在快刀伺服機構的設計中，實現長行程輸出的同時必然會降低機構的固有頻率，影響系統帶寬和系統加工效率，因而在機構設計時需要綜合考慮行程和固有頻率性能選擇機構參數。

本文所設計的長行程快刀伺服機構材質選用具有優越變形能力的鋁合金AL-7075，材料特性如表1所示。根據上述理論分析，結合所設計機構的行程和固有頻率頻率指標，同時考慮機構的應力及尺寸，選擇機構參數如表2所示。

為驗證所設計機構的性能及理論分析的有效性，采用ANSYS軟件對所設計機構進行有限元仿真。對機構施加450 N輸入力時機構的位移變形如圖6所示。

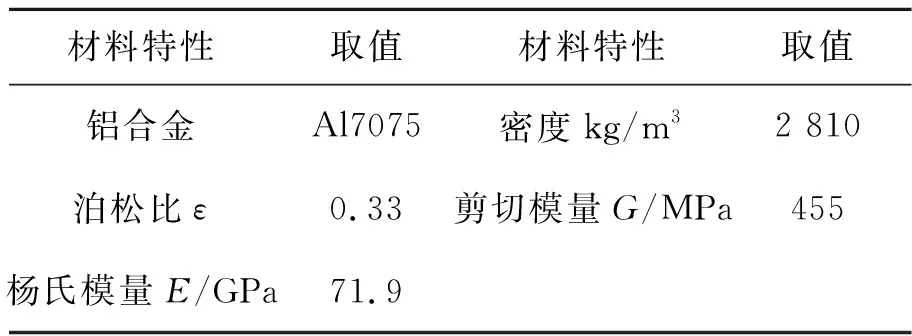
表1 機構材料參數

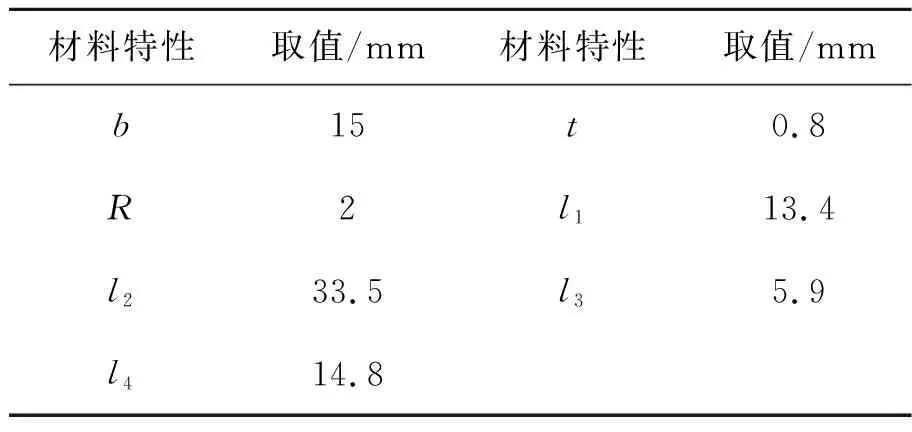
表2 機構參數

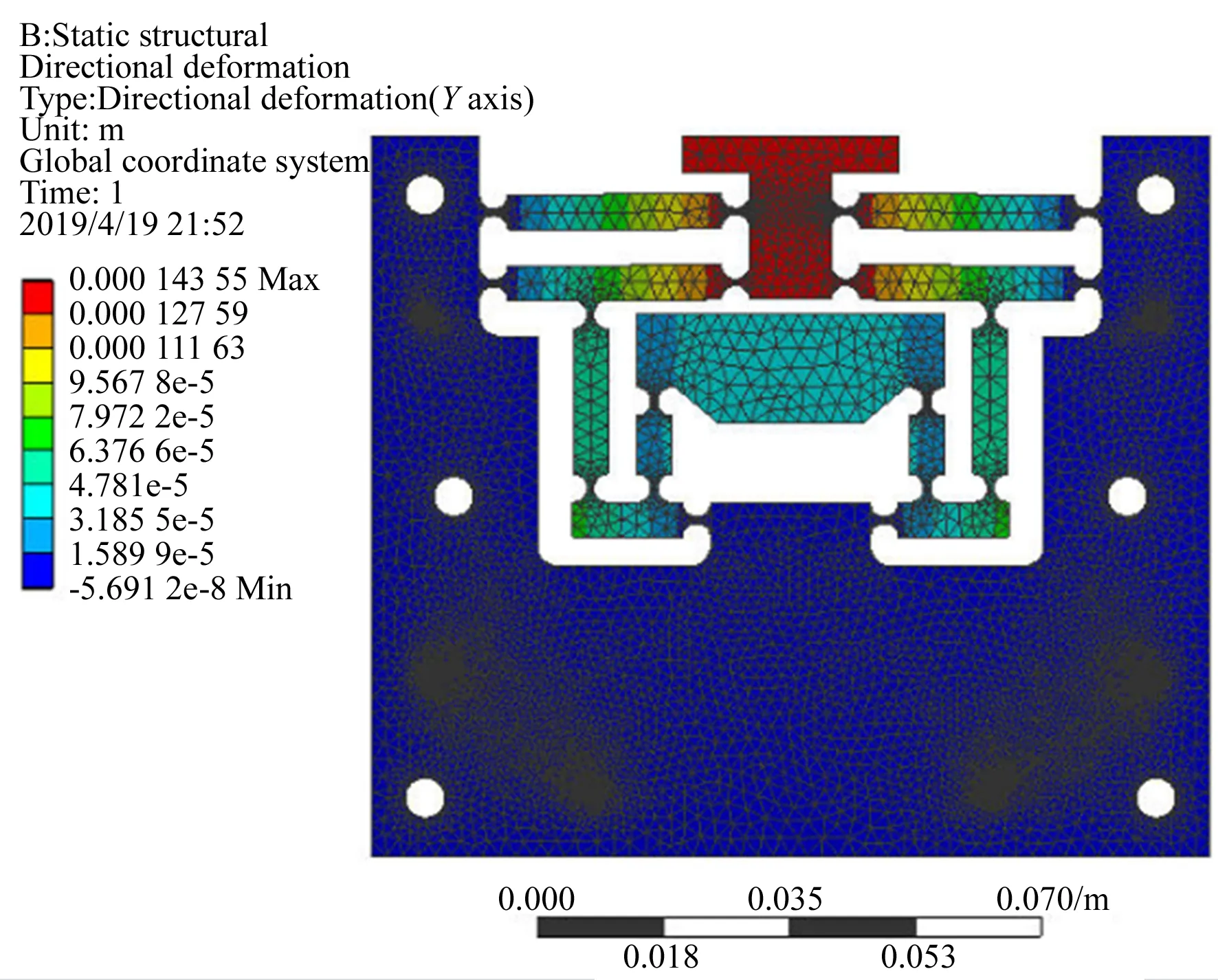
圖6 FTS機構位移變形Fig.6 Displacement deformation of designed FTS

從仿真結果中可知對稱布置的機構設計消除了非工作方向的寄生位移。進一步的，對機構進行有限元模態分析，有限元仿真和理論計算得到的機構剛度和一階固有頻率結果如表3所示。理論計算和有限元仿真結果基本一致，驗證了理論模型的有效性。

表3 有限元仿真值與理論值對比

Tab.3 Comparison between FEA and theoretical results

理論值有限元值誤差等效剛度2.9 N/μm3.1 N/μm6.4%一階模態678 Hz689 Hz1.6%

4 實驗測試

以優化設計的機構參數，采用超精密線切割的方式對所設計的長行程快刀伺服機構進行了加工，并建立了如圖7所示的實驗系統。實驗中采用Noliac公司的壓電陶瓷(NAC2014-H28)，其最大行程42.9 μm，采用線性光柵作為位移傳感器。

圖7 FTS系統實驗裝置Fig.7 Experimental setup of the designed FTS system

4.1 靜態性能實驗

對系統施加0～110 V的正弦波電壓信號，得到機構的輸出行程特性，如圖8所示。設計的快刀伺服機構可以達到100 μm的行程輸出，這一行程可以滿足大多數光學自由曲面的加工。

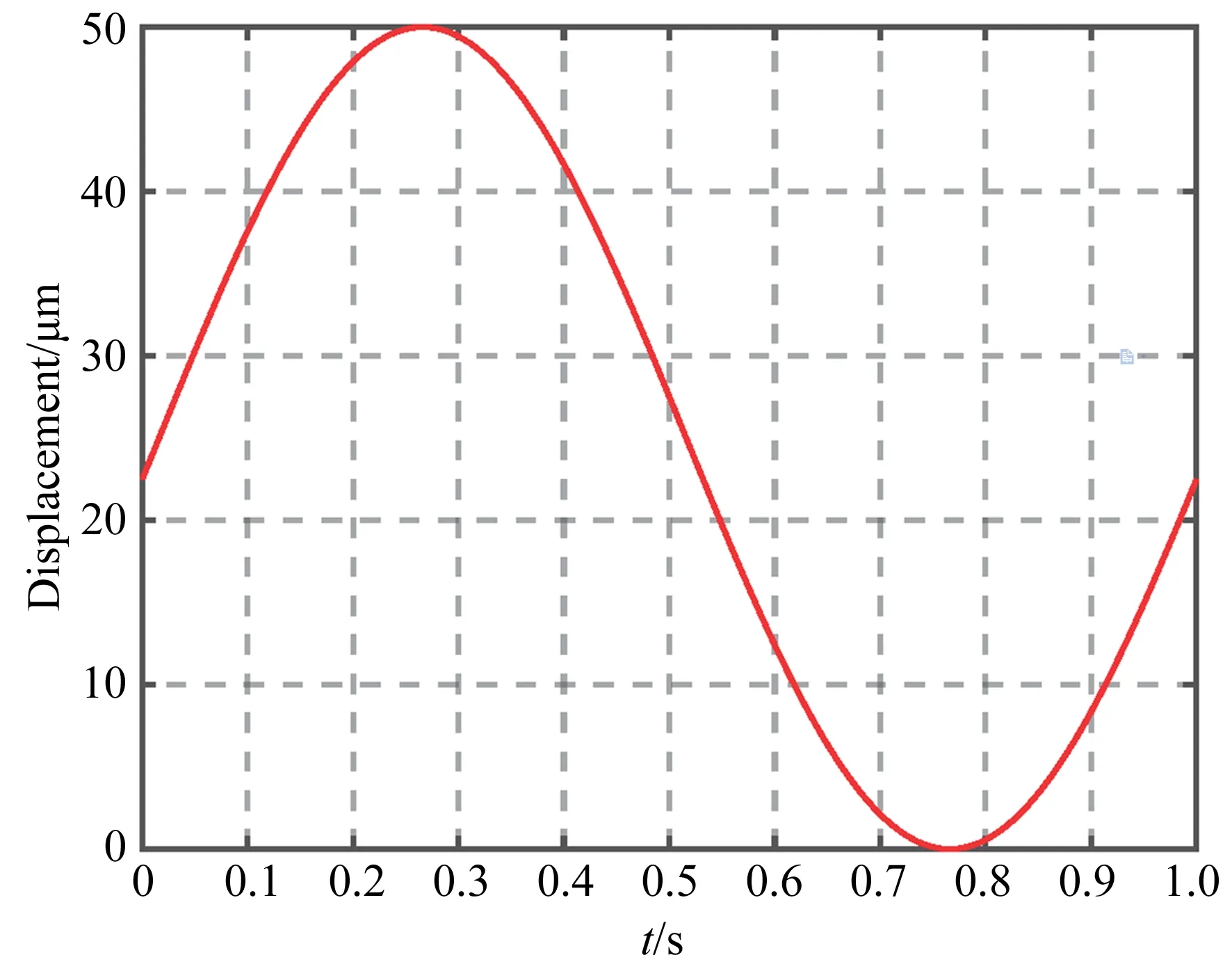
圖8 FTS機構行程測試Fig.8 Stroke test of the designed FTS

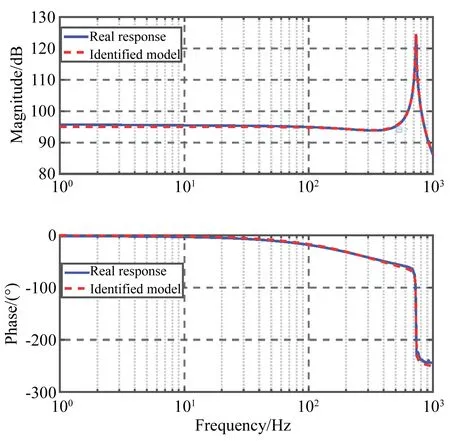
圖9 實際系統和辨識系統的頻率響應Fig.9 Frequency responses of real and identified models

4.2 動態性能實驗

為得到系統的動力學模型，對壓電陶瓷施加1～1 000 Hz的正弦掃頻信號，采用DFT實時控制算法得到系統的頻率響應數據，進一步辨識得到實驗系統的動力學模型，如圖9所示。

辨識得到系統的傳遞函數模型如式(9)所示：

G(s)=

(19)

系統的動態實驗得到其固有頻率為730 Hz，略高于理論和仿真值，這是由于加工及安裝誤差增大了系統的剛度和固有頻率。在此固有頻率下，系統可以實現較高的帶寬和頻率響應，從而保證系統的加工效率。

4.3 閉環跟蹤實驗

對圖1所示的加工系統，采用坐標轉換法，則待加工自由曲面z=f(x，y)在柱面坐標系(ρ，θ，z)中可表示為：

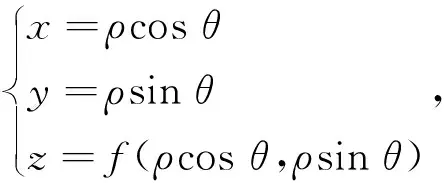
(20)

其中：ρ為工件沿x軸的位移，θ為主軸的旋轉角度，z為刀具在快刀伺服系統帶動下沿z軸的進給位移。

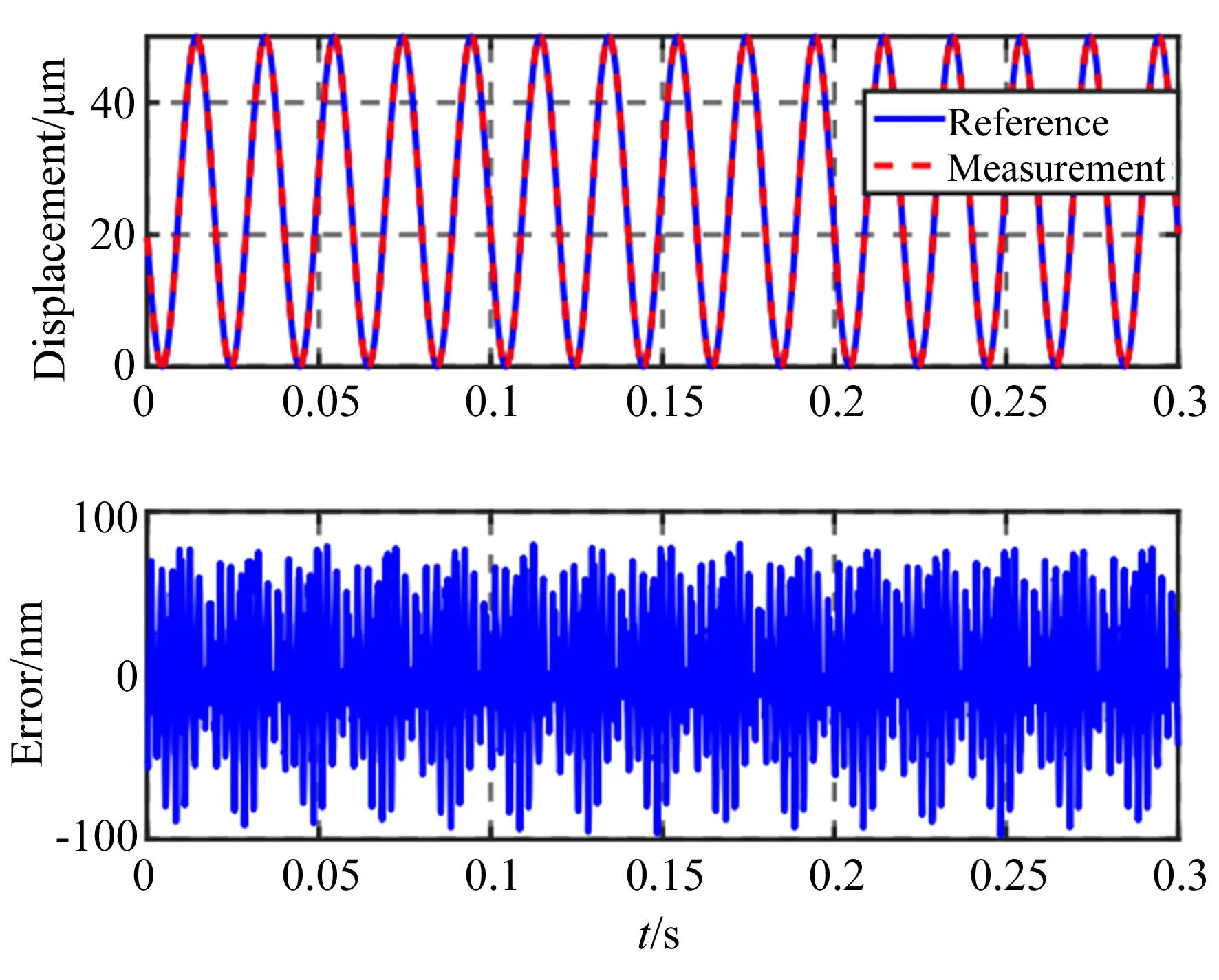
圖10 軌跡跟蹤和跟蹤誤差Fig.10 Trajectory and tracking errors

在上述加工過程中，系統常常需要跟蹤連續的正弦信號。為了評估系統的跟蹤性能，實驗跟蹤幅值25 μm、頻率50 Hz的正弦信號。根據式(19)得到的系統動力學模型，采用基于PID鎮定的并聯內模方法對系統進行閉環控制[20]，實驗結果如圖10所示。對50 Hz信號的跟蹤誤差為±90 nm，為其行程的0.36%，驗證了系統具有良好的跟蹤性能。

5 結 論

本文設計了一種壓電陶瓷驅動的長行程快刀伺服機構，采用對稱式結構及二級放大機構，實現了壓電陶瓷驅動的快刀伺服機構的長行程輸出性能并消除了非工作方向的寄生位移。

針對所設計的長行程快刀伺服機構，采用偽剛體模型和拉格朗日原理建立了機構的動力學模型，并對設計的機構進行了有限元仿真和實驗驗證，仿真和實驗結果與理論模型有良好的一致性。實驗驗證表明本文設計的快刀伺服機構兼顧了機構的行程和固有頻率性能，可以達到100 μm的行程輸出，同時具有730 Hz的固有頻率。閉環跟蹤試驗也驗證了系統良好的信號跟蹤性能。

本文設計的壓電陶瓷驅動的長行程快刀伺服機構對提升快刀伺服機構的應用范圍和加工精度具有參考意義。