基于差分進化算法的輔助燃油系統燃油轉輸參數優化

龔 昊

(中國商用飛機有限責任公司上海飛機設計研究院，上海 201210)

飛得更高、更快、更遠一直是航空領域追求的目標。在飛機的氣動外形和動力裝置不進行改進的情況下，通常需要增加飛機的載油量才能實現飛機航程的增加或留空時間的延長。對于民用飛機而言，在改進原機油箱以增加載油量以外，更為便利的方式是在飛機機身貨艙內安裝輔助油箱，以存儲更多的燃油[1]。通過輔助燃油系統將輔助油箱中的燃油轉輸至飛機的基本油箱中，供發動機消耗。國外采用這種方式的機型包括B737、B777、A319、ERJ190、世襲1000等。中國在民機加裝輔助油箱方面的研究很少，目前尚無加裝輔助油箱的國產民用飛機交付使用。

Fasanella等針對B737機身下部設輔助油箱的情況，建立了全尺寸三維有限元模型，并利用非線性瞬態動力學軟件進行了墜落撞擊仿真[2]。Gavel等針對帶有輔助油箱的飛機，基于飛機級頂層需求，對燃油轉輸系統進行了概念設計[3]。劉勝君對加裝了輔助油箱的BBJ公務機和ACJ公務機的特點進行了介紹[4]。劉德剛等對輔助油箱的設計、布置和安裝進行了介紹，對采用增壓氣體轉輸燃油的輔助燃油系統的設計特點進行了分析[1]。

在輔助燃油系統設計中，燃油轉輸相關參數的確定是方案設計的核心，憑借工程經驗人為給定的方式難于獲得最優方案，可以考慮使用優化算法對設計方案進行優化。

隨著人們對各種優化問題的關注，目前發展了諸多各具特點的優化算法，如遺傳算法、粒子群算法等。其中，差分進化算法由Storn和Price于1997年正式提出，是一種基于種群的啟發式進化算法[5]。差分進化算法以其算法結構易執行、優化效率高、參數設置簡單、優化結果穩健等優點，受到諸多研究者的關注。Das等綜述了差分進化算法的研究現狀，并從基本概念、算法構造、控制參數、變量范圍、優化目標等方面對差分進化算法進行了理論分析[6]。丁青鋒等概述了差分進化算法的研究概況以及存在的問題，綜述了差分進化算法在控制參數、差分策略、種群結構以及與其他最優化算法混合等4個方面的改進策略，并討論了各自的優缺點[7]。

為了對燃油轉輸參數方案進行優化，本文將輔助燃油系統燃油轉輸設計過程抽象成約束優化問題，并對差分進化算法進行改進，在此基礎上進行燃油轉輸參數的優化。通過本文的研究，完成了對輔助燃油系統燃油轉輸優化設計問題的求解，同時也為差分進化算法的應用研究提供了新的參考。

1 輔助燃油系統燃油轉輸工作原理

圖1為本文所研究的輔助燃油系統進行燃油轉輸的示意圖，輔助油箱采用閉式通氣系統，利用飛機客艙的增壓空氣或發動機引氣作為壓力源，將輔助油箱中的燃油轉輸至原機的基本油箱。燃油轉輸過程的本質是用同體積的增壓空氣替代從輔助油箱轉輸出的燃油，這是當前民用飛機輔助油箱采用的主流方式[1]。

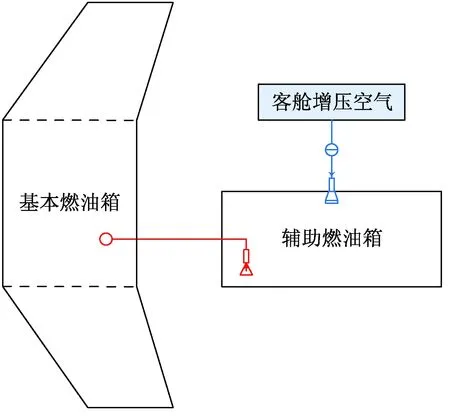
圖1 輔助燃油系統燃油轉輸示意圖Fig.1 Schematic diagram for fuel transfer of the auxiliary fuel system

理論上，燃油從輔助油箱向基本油箱的轉輸可能發生在整個飛行任務的任意飛行階段。對于民用飛機而言，飛行時間最長的是巡航階段，也是燃油轉輸最主要的階段。因此，為簡化問題，假設燃油轉輸僅在巡航階段進行。

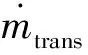
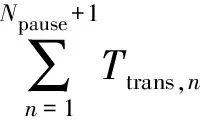
2 燃油轉輸優化設計問題

通常，滿足要求的燃油轉輸參數方案不止一個，可以將其作為約束優化問題進行求解：

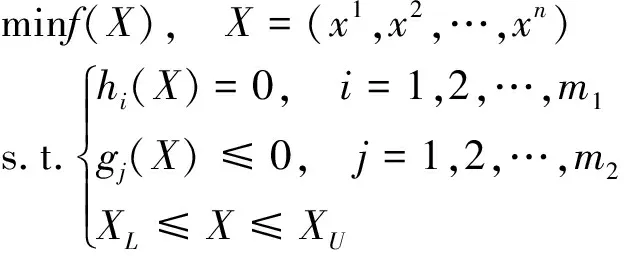
(1)

式(1)中：f(X)為目標函數：X=(x1,x2,…,xn)是優化變量；XU和XL分別為優化變量的上下限；hi(X)為等式約束；gj(X)為不等式約束。

輔助燃油系統燃油轉輸參數優化設計問題可描述如下。

(2)目標函數f(X)如式(2)所示，求解目標為完成燃油轉輸的總時長最短：

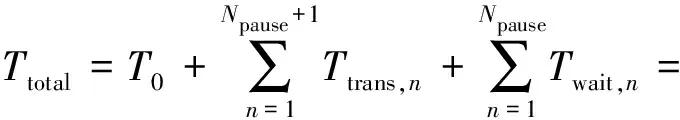
(2)

式(2)中：T0為從巡航開始到燃油轉輸開啟所需的時間；Wmain_ini為開始巡航時的基本油箱載油量；Waux為輔助油箱總的載油量。轉輸中斷次數Npause由式(3)計算，“?」”表示向下取整。

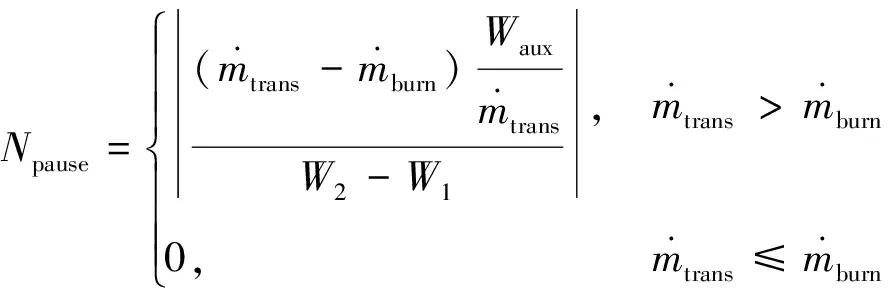
(3)

(3)約束條件1是當完成燃油從輔助油箱向基本油箱的轉輸時，基本油箱的載油量不少于備用油量，如式(4)所示：

(4)

(4)約束條件2是燃油轉輸中斷的次數不大于預設值，即0≤Npause≤Nmax，如果要求燃油轉輸過程不得出現中斷，則Npause=Nmax=0。

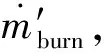
(5)

式(5)中：p′trans和ptrans分別為單、雙發運行時的客艙壓力；p′env和penv分別為單、雙發運行時的外界大氣壓，客艙壓力與飛行高度的關系為已知條件。

當單發運行時，在規定的時間Tsingle內，基本油箱的載油量不得下降至備用油量：

(6)

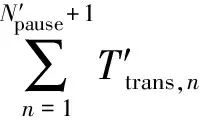
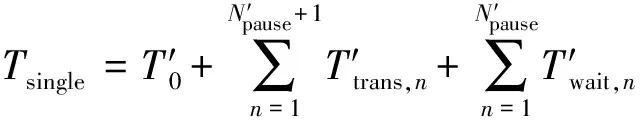
(7)

3 差分進化算法改進及驗證

差分進化的基本原理是從隨機生成的初始種群開始，通過反復進行變異、交叉和選擇等操作來模仿生物界的進化過程，不斷使種群中的個體向著適應環境的方向發展(保留適應環境的個體)，即逐漸逼近問題的最優解。文獻[5, 6]對差分進化算法的概念、計算過程等進行了詳盡的闡述，不再贅述。為了達到更好的算法穩定性與效率，在基本差分進化算法的基礎上進行了改進。

3.1 改進差分進化算法

使用的改進差分進化算法的計算流程如圖2所示。變異操作采用DE/best/2的差分形式，交叉操作采用二項式交叉，選擇操作采用貪婪算法，迭代計算中采用精英保留策略。迭代過程將持續進行直到獲得最優解或達到最大迭代次數限制。差分進化算法的基本概念和操作過程詳見文獻[6]，下面僅介紹本文對差分進化算法的改進。

圖2 改進差分進化算法計算流程Fig.2 The modified differential evolution algorithm calculation flow chart

3.1.1 基于自適應懲罰函數的適應度計算

為求解式(1)所示的約束優化問題，采用懲罰函數法將適應度函數fitness(X)構建為帶有懲罰函數的非約束優化問題的目標函數fp(X)，如式(8)～式(10)所示。適應度函數最小值對應優化問題的最優解。構建目標函數時，將懲罰因子選取為關于自變量的函數[8]，以解決懲罰因子的確定問題。此外，為加快收斂速度，構建目標函數時，還借鑒了“多級懲罰”的思想[9]，即對違反約束大的段給予較大的懲罰而違反約束小的段給予較小的懲罰。

fitness(X)=fp(X)=f(X)+C(X)p(X)

(8)

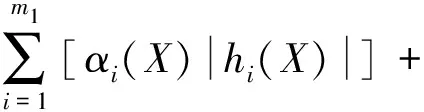
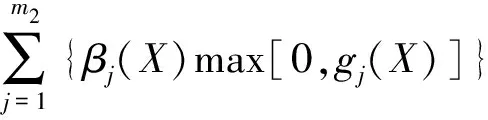
(9)

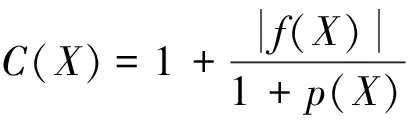
(10)

式中：C(X)為多級懲罰因子；p(X) 為懲罰函數；αi(X)和βj(X)為自適應懲罰因子，分別如式(11)和式(12)所示：

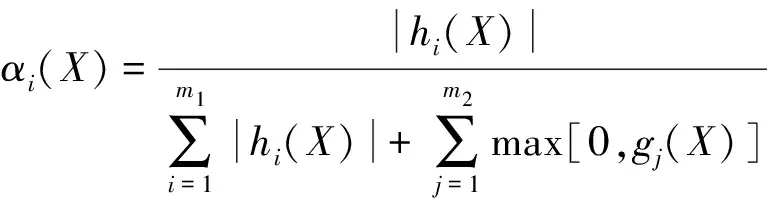
(11)

(12)

3.1.2 采用自適應縮放因子的變異操作

變異操作中，最重要的參數是縮放因子F，其取值對于種群的多樣性有很大影響。采用基于種群個體適應度的時變計算策略，如式(13)所示[10]。

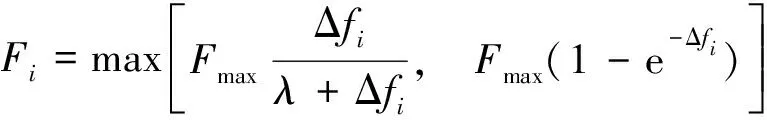
(13)

式(13)中：控制因子Fmax需預先給定數值；f(Xbest)為當前代種群中適應度最優個體的適應度，則參數Δfi和λ分別如式(14)和式(15)所示。

Δfi=|f(Xi)-f(Xbest)|

(14)

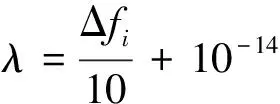
(15)

3.1.3 采用自適應交叉概率因子的交叉操作

交叉操作中，最重要的參數是交叉概率因子Cr。采用基于種群個體適應度的時變計算策略，如式(16)所示[11]。

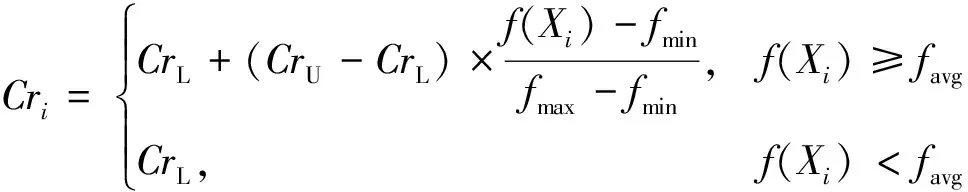
(16)

式(16)中：fmin、fmax和favg分別為種群個體的最小、最大和平均適應度；CrU和CrL分別為交叉概率因子上下限。

3.1.4 高斯變異

為了防止種群進化階段陷入局部最優，補充了高斯變異操作[12]。針對當前種群適應度最優的個體，通過高斯變異產生一個新的最優個體，將二者中適應度更好的個體作為最終的當前代最優個體。該操作并非每一次計算都進行，而只在種群相似度達到一定程度之后才進行。

從差分進化算法的角度來看，一組優化變量值就代表了種群中的一個個體，即一個燃油轉輸參數候選方案；將燃油轉輸計算過程作為優化問題的適應度函數，通過對目標函數最佳適應度的計算獲得最優的燃油轉輸參數方案。

3.2 數值實驗

為了驗證發展的改進差分進化算法對求解約束優化問題的有效性，使用以下典型測試函數對算法進行測試。文獻[13]對這些測試函數進行了圖形化顯示。

(1)測試函數1：Sphere函數為

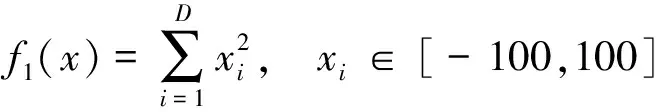
(17)

式(17)中：D為維數。該函數理論最優值為0，對應的最優點xi=0。

(2)測試函數2：Rosenbrock函數為

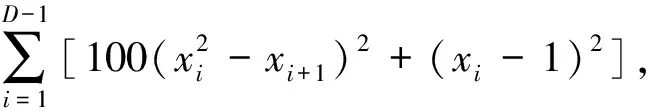
xi∈[-2.048,2.048]

(18)

該函數理論最優值為0，對應的最優點xi=1。

(3)測試函數3：Rastrigin函數為

xi∈[-5.12,5.12]

(19)

該函數理論最優值為0，對應的最優點xi=0。

(4)測試函數4：Ackley函數為

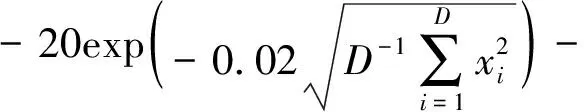
xi∈[-32,32]

(20)

該函數理論最優值為0，對應的最優點xi=0。

數值實驗中，維數D取為10，種群大小Np取為優化變量個數的10倍，即Np=100，縮放因子F的上限取為1.0，交叉概率因子Cr的上下限分別取為0.9和0.1，最大進化代數取為500。為了減小隨機干擾，對每個問題都重復進行50次實驗。

表1為本文算法對測試函數的計算情況。結果表明，本文發展的改進差分進化算法的求解情況較為理想，可有效求解約束優化問題。

表1 測試函數計算結果

4 輔助燃油系統燃油轉輸參數優化

基于上述改進差分進化算法，進行輔助燃油系統燃油轉輸參數優化計算分析。優化計算所需限制參數等計算輸入如表2所示，燃油轉輸參數變化范圍如表3所示。

表2 計算輸入

表3 優化參數變量范圍

優化計算過程中，燃油轉輸參數和優化問題適應度隨進化代數的變化情況如圖3～圖6所示。可見，在500代進化計算內可以求得最優解，本文發展的改進差分進化算法對燃油轉輸參數方案的優化求解有效。

圖3 巡航狀態燃油轉輸速率隨進化代數的變化情況Fig.3 Optimization calculation iteration history of the fuel transfer flowrate of cruise condition

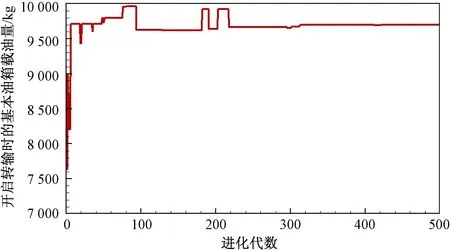
圖4 開啟轉輸時的基本油箱載油量隨進化代數的變化情況Fig.4 Optimization calculation iteration history of the main tank fuel quantity when fuel transfer starts

圖5 中斷轉輸時的基本油箱載油量隨進化代數的變化情況Fig.5 Optimization calculation iteration history of the main tank fuel quantity when fuel transfer pauses

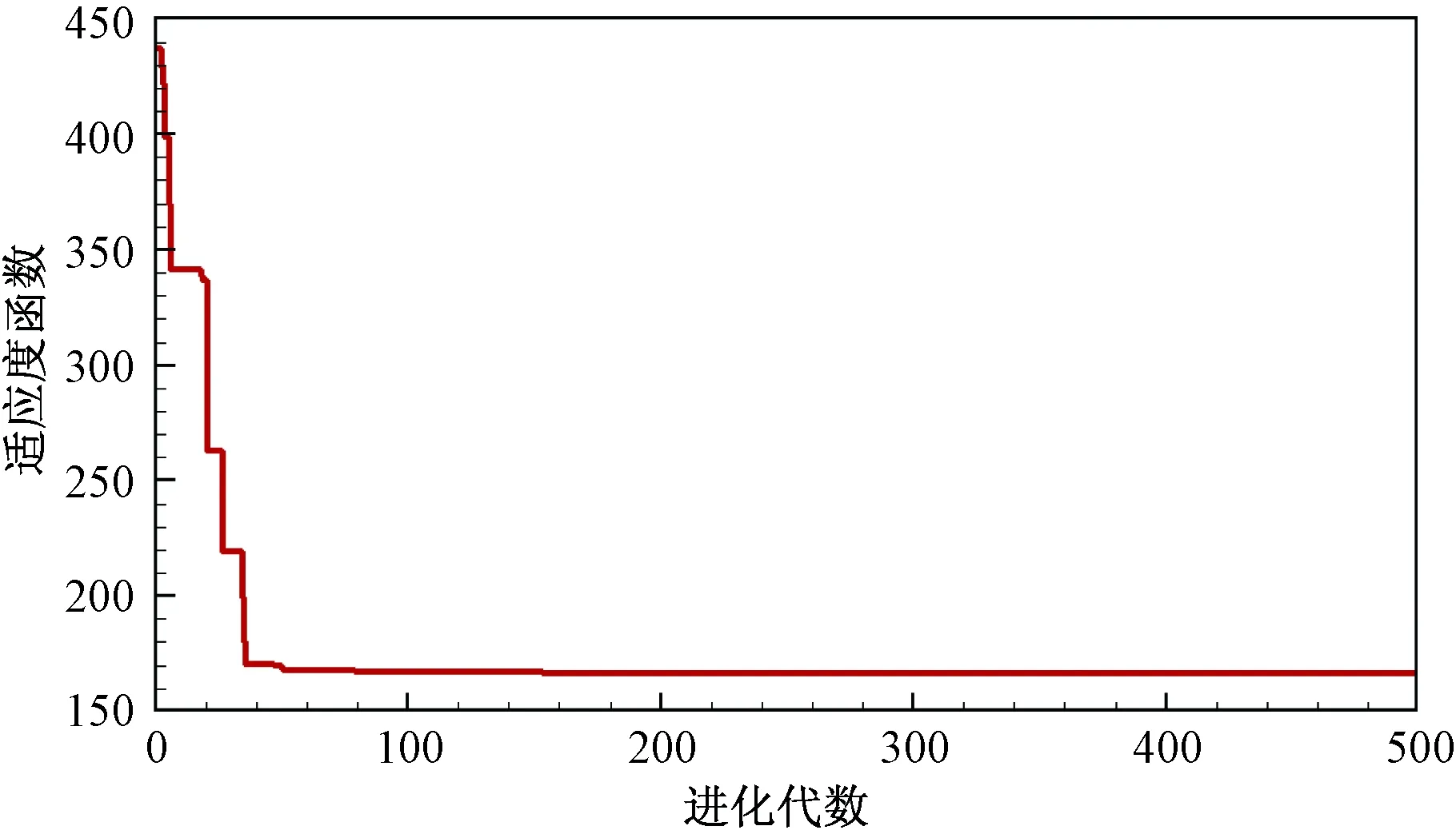
圖6 適應度函數隨進化代數的變化情況Fig.6 Optimization calculation iteration history of the fitness

優化計算得到的燃油轉輸參數方案及其燃油轉輸性能如表4所示。可以看出，優化計算結果可滿足各項限制和優化約束條件。

基于表4中優化得到的燃油轉輸參數方案，對雙發運行情況下的燃油轉輸過程可解析如下：①飛機經過10 min的雙發運行，基本油箱的載油量從10 000 kg下降到9 700 kg；②此時，開啟從輔助油箱向基本油箱的燃油轉輸；③以速率31.9 kg·min-1進行連續的燃油轉輸，轉輸過程持續157 min；④此時，基本油箱載油量上升至10 000 kg，燃油轉輸過程結束。

除了燃油轉輸參數方案優化計算結果以外，表4還列出了基于不同的燃油轉輸策略的計算結果。

對于雙發運行的情況，各策略與最優方案對比如下：①策略一與最優方案相似，但由于轉輸速率低于最優方案，轉輸用時較最優方案多10 min；②策略二和策略三開啟轉輸時的基本油箱載油量與最優方案相同，但轉輸速率遠高于最優方案，使得轉輸中斷次數很多；③策略四、策略五和策略六開啟轉輸時的基本油箱載油量低于最優方案，轉輸速率高于最優方案，轉輸過程存在一到兩次的中斷，由于轉輸開啟前用時和轉輸中斷等待用時較長，使得完成燃油轉輸所需時間多于最優方案；④策略七與最優方案相比，轉輸開啟前無需等待，但由于燃油轉輸速率低于最優方案，使得轉輸用時較長。

表4 優化計算結果及與給定的燃油轉輸策略的對比

對于單發運行的情況，各策略與最優方案對比如下：①策略一與最優方案相似，但轉輸結束時基本油箱的載油量低于最優方案；②策略二和策略三轉輸中斷次數較多；③策略四、策略五和策略六轉輸結束時的基本油箱載油量低于最優方案；④策略七為連續轉輸，轉輸結束時的基本油箱載油量與最優方案接近。

通過上述對比可知，燃油轉輸參數優化方案可以保證雙發運行情況下和單發運行情況下的性能最優，體現在雙發運行情況下完成燃油轉輸的總時長最短且轉輸中斷次數最少，同時在單發運行情況下轉輸完成時的基本油箱載油量接近滿油。

5 結論

對差分進化算法進行了改進，發展了輔助燃油系統燃油轉輸參數優化計算方法，在此基礎上對燃油轉輸進行了優化計算。得出主要結論如下。

(1)在分析輔助燃油系統燃油轉輸工作原理的基礎上，將燃油轉輸設計過程抽象成可求解的約束優化問題，為燃油轉輸參數優化提供了解決思路。

(2)對差分進化算法進行了改進，通過典型測試函數的測試，表明了所發展的改進差分進化算法對約束優化問題求解的有效性。

(3)在給定的計算輸入和變量范圍的情況下，使用改進差分進化算法計算得到了燃油轉輸參數最優方案，其燃油轉輸用時短，轉輸中斷次數少，結束轉輸時基本油箱的載油量高。

(4)與給定的燃油轉輸策略的計算結果對比表明，燃油轉輸參數優化方案在雙發運行和單發運行情況下的性能都優于其他轉輸策略。