格構式鋼柱在沖擊作用下動態響應的有限元分析

崔 凱， 張永勝， 郭昭勝

(太原理工大學土木工程學院， 太原 030024)

格構式鋼柱多由型鋼或鋼板設計成的雙軸或單軸對稱截面，具有環保、高效的特點，擁有較好的承載力和抗扭性能，是常見的鋼結構類型，在工民建領域具有重要的地位。然而建筑結構在服役期間，各種類型的結構及其部件會不可避免地受到不同程度的沖擊，譬如以熱力管道活動支架為例的懸臂鋼柱在使用過程中遭到行駛車輛的意外沖擊，或者廠房中由于屋架作用而視為固簡約束的排架柱因吊車吊起重物時的操作不慎而受到側向沖擊碰撞等，會對人類造成財產損失甚至對人身安全造成威脅。隨著格構式構件在鋼結構領域的廣泛應用，對其沖擊荷載下的動態響應和力學性能的研究變得尤為重要。

中外學者對鋼管及鋼管組合結構、實腹式型鋼結構、鋼筋混凝土等結構的沖擊受損做了大量研究，蔡健等[1]、王瀟宇等[2]、Huang等[3]對不同形式和約束情況的鋼管組合結構進行落錘沖擊試驗，得出壁厚、尺寸、形式、重量等因素是影響鋼管組合結構側向沖擊性能的重要因素，并簡化計算方法；王蕊等[4]、崔娟玲等[5]、弓磊等[6]對研究受沖擊后H型鋼柱的力學性能進行研究，計算其剩余承載力系數，得出沖擊能量與局部損傷變量之間的線性的函數關系；Demartino等[7]、Cai等[8]、Pham等[9]對鋼筋混凝土構件進行了一系列沖擊試驗，并與經驗公式進行對照,研究其沖擊作用下的力學性能。

目前，中國有關格構式構件在沖擊荷載下的動態響應和力學性能文獻較少[10-11]，對格構式構件的研究可以進一步挖掘開發，因此，基于Abaqus/Explicit的顯示中心插值算法，探索在不同沖擊作用下，懸臂式鋼柱在側向沖擊作用下的動態響應，并對其抗沖擊性能進行研究。

1 試驗簡介以及模型驗證

1.1 試驗概述

文獻[11]通過控制落錘下落高度對6個規格相同的格構式鋼柱進行側向沖擊試驗，試件為兩端鉸支約束，材料為Q235低碳素鋼，柱肢規格為L50 mm×5 mm，兩端綴板采用-5 mm×80 mm×150 mm長綴板，中間綴板采用-5 mm×80 mm×100 mm鋼板，各綴板間距100 mm，試件兩端焊接-20 mm×220 mm×220 mm的端板，試件總長度為1.44 m。落錘總重203.9 kg，底面尺寸為80 mm×30 mm，下落高度分別為0.5、0.7、1.1 m。試驗采用動態應變儀記錄試件在沖擊力作用下沖擊力時程曲線，并記錄肢件測點相對變形量。

1.2 模型的建立

采用Abaqus/Explicit有限元程序對文獻[11]中格構式鋼柱落錘沖擊試驗進行模擬和分析。鋼柱和落錘采用Solid實體單元組合而成，其中落錘通過的*Rigid Body約束為剛體，質量由密度控制。鋼材采用文獻[12]提供的應力-應變關系模型，關系曲線分為：彈性、彈塑性段、塑性、二次流塑四個階段。由于在沖擊荷載下應變率強化作用，為達到預期的模擬目標，采用Cowper-Symend模型描述材料應變率，模型中參數由文獻[6]統一取D=6 844 s-1、p=3.91。材料參數采用文獻[11]實測數據如表1所示。

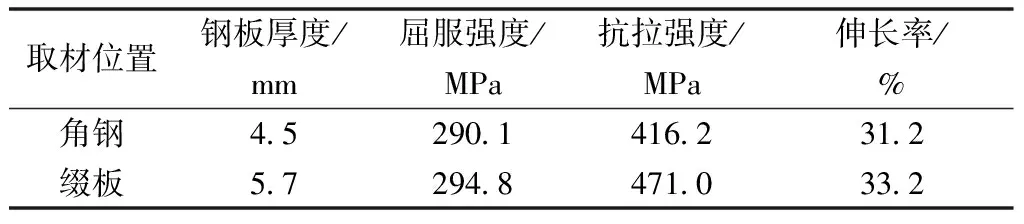
表1 鋼材的材料性能參數Table 1 Material properties of steel

模型分析時給落錘施加不同沖擊速度反映高度，落錘和鋼柱表面之間接觸定義為通用接觸，其中法線方向定義為“hard”接觸，切向方向按照“penalty”接觸，摩擦系數設為0.4。另外綴板、角鋼、端板之間焊接連接，采用*tie約束，即視為各個焊縫在沖擊過程中不發生相對位移。模型中通過*coupling約束將構件端板節點耦合，設置參考點轉角與位移使得試件為兩端簡支約束。網格劃分過程中，模型全部采用C3D8R單元劃分，網格最大不超過10 mm，沖擊試驗模型網格劃分圖如圖1所示。

圖1 鋼柱受沖擊有限元模型Fig.1 Finite element model of steel columnsubjected impact load

1.3 模型的驗證

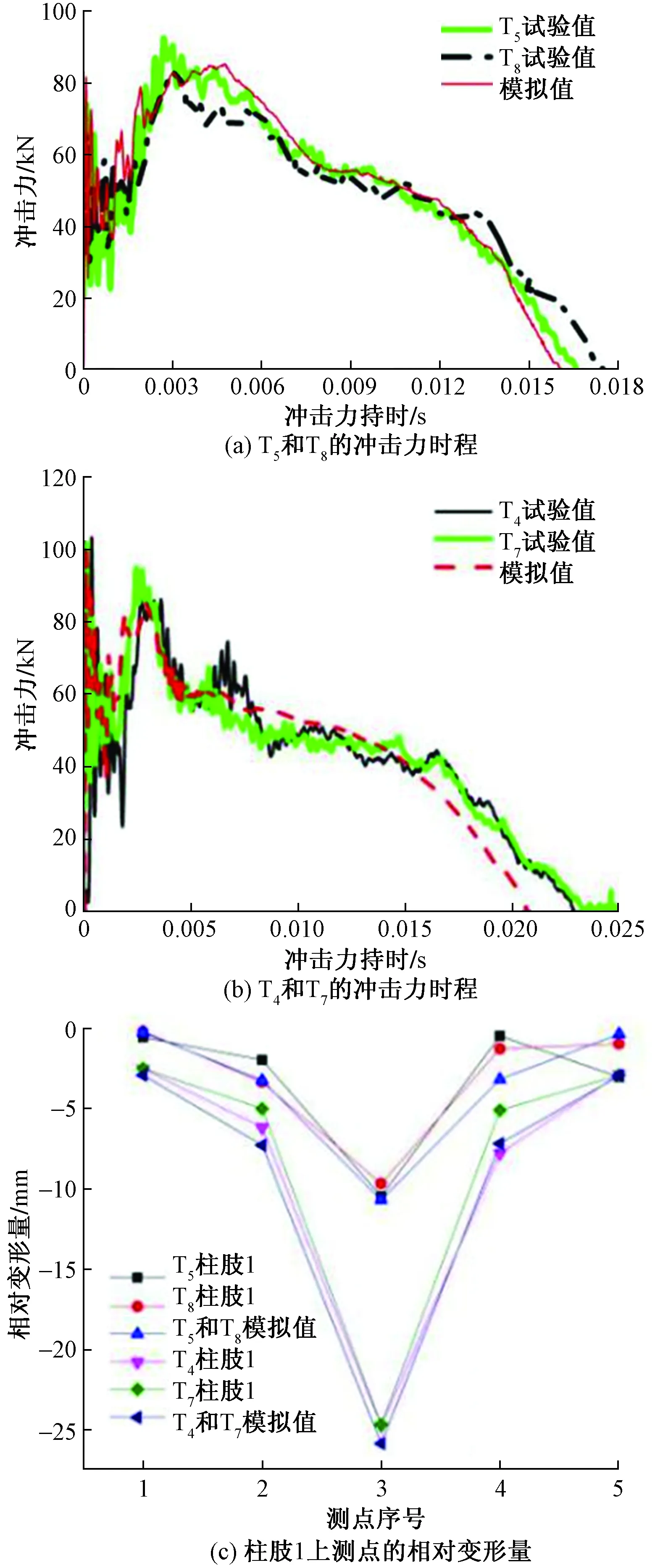
圖2 數值模擬與試驗對比Fig.2 Comparison between numerical and experimental

試驗中每兩個試件為同一工況，圖2給出工況1(試件T5、T8)與工況2(試件T4、T7)下沖擊力時程曲線與柱肢1相對變形量的數值模擬與試驗結果對比圖。由圖2可知，兩者沖擊力時程曲線吻合良好，沖擊力峰值與沖擊力平臺值非常接近，沖擊力持時比試驗稍短。試驗與模擬柱肢1測點相對變形量的偏差較小，模擬值略大于試驗值,表2給出了柱肢中間測點的相對變形量，柱肢跨中相對變形量最大差值在2.32 mm以內，證明模型的有效性。

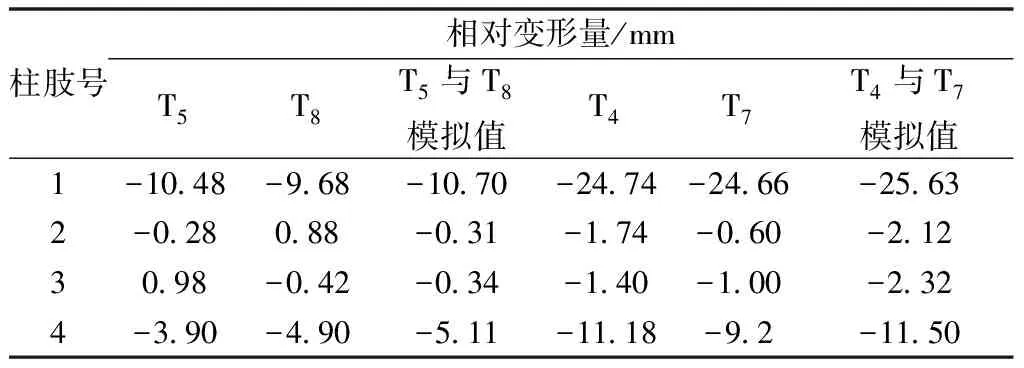
表2 柱肢中間測點的相對變形量Table 2 Relative deformation of measuringpoints on limb middle

注：柱肢撓度值為正值時，撓度向上；柱肢撓度值為負值時，撓度向下。

2 格構式鋼柱的有限元分析

2.1 模型的建立

基于上述結果比較，證明該數值方法具有一定的可靠性。現以某廠房熱力管道活動支架的懸臂格構式鋼柱為例，研究其在側向沖擊下的力學性能，研究不同沖擊位置與沖擊能量下懸臂式格構柱的抗沖擊性能。

在上述試驗的模型的基礎上，約束條件改為一端固定，一端自由。落錘底面尺寸為30 mm×180 mm，質量保持不變。沖擊速度控制根據規范GB 4387—2008[13]有關限速要求選用沖擊速度依次為4.75、5.42、6.34 m/s，沖擊位置為綴板中心處，具體沖擊位置如圖3所示，試件基本參數如表3所示。

圖3 沖擊位置圖Fig.3 Positions drawing of impact

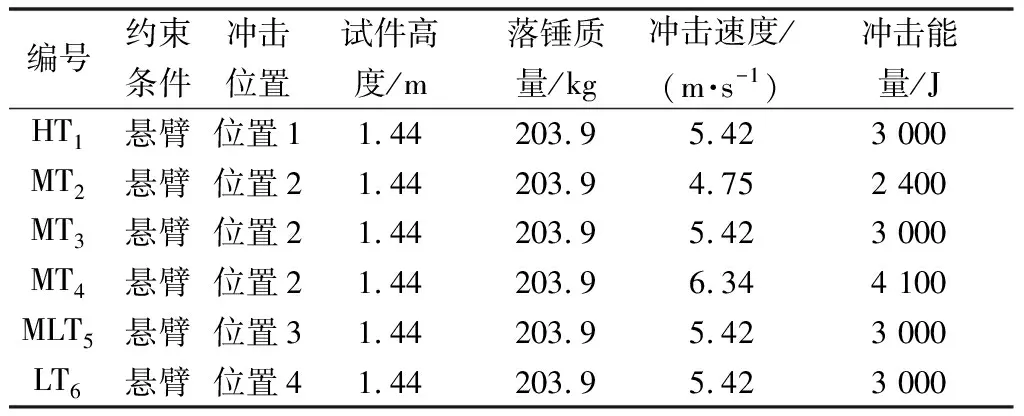
表3 試件基本參數Table 3 Basic parameters of specimens

2.2 破壞形態

圖4為不同沖擊位置與沖擊能量下格構式鋼柱的變形特征及破壞形態，由圖4可知，各個構件均出現不同程度的屈曲變形，隨著沖擊能量以及沖擊位置的提高，懸臂式鋼柱的整體變形情況，有著明顯增大的趨勢。對于沖擊作用在跨中及以上位置(位置1、位置2)的懸臂試件，受沖擊部位并未發生明顯的局部凹陷，且頂端具有較大側移率，整體沿鋼柱受沖擊方向呈斜直線變形;對處于沖擊位置3的MLT5構件，雖發生較大側移，但變形為斜折線狀，并以沖擊處為折線拐點；而沖擊位置4的懸臂試件LT6，受撞處局部屈曲情況嚴重，沖擊點朝兩端位置方向，水平側移不斷減小，自由端未發生明顯側移,表現出良好的抗沖擊性能。

圖4 試件整體破壞形態圖Fig.4 Global failure patterns charts of specimens

圖5為懸臂式鋼柱根部典型破壞形態，由圖5可知，在對試件跨中進行沖擊作用時，懸臂式試件MT4根部綴板處由于彎曲效應大于剪切效應，柱肢受壓而產生明顯的局部鼓曲現象，而沖擊作用在位置4的懸臂式試件LT6，由于沖擊位置低，試件根部不易形成塑性鉸，破壞時以剪切變形為主。

圖5 典型柱根部破壞形態Fig.5 Typical local failure patterns of column end

2.3 沖擊力時程曲線

圖6(a)給出了沖擊能量影響下的沖擊力時程曲線，隨著沖擊能量的增加，沖擊力趨勢基本保持不變，能量大小與沖擊力發展無明顯影響。懸臂試件在跨中及其以上的位置(位置1、位置2)受到沖擊作用時，其沖擊力時程曲線大致可以分為四個階段：峰值段、二值峰值段，平臺值段、卸載階段，由于自由端的約束能力較弱，試件發生變形后發生反彈，與落錘再次接觸，進入二次峰值段，該段類似拋物線的時程曲線，且該段的最大值只有最大沖擊力峰值的1/4～1/3。當沖擊點位置與自由端的距離的縮短時，二次峰值段的最大值增大，該段作用時間提前，持時減小。

圖6(b)所示為沖擊力位置影響下沖擊力時程曲線，可知對于沖擊位置較低(位置4)的LT6懸臂試件，因破壞以剪切變形為主，整個沖擊過程與兩端簡支構件類似，均經歷了沖擊力峰值段、平臺值段、卸荷段三個階段[11]；試件MLT5的與試件LT6相比受到固定端的約束稍弱，沖擊力時程曲線發展趨勢與沖擊點位于跨中及以上位置(位置1、位置2)的懸臂鋼柱相似，但并未產生二次峰值段。

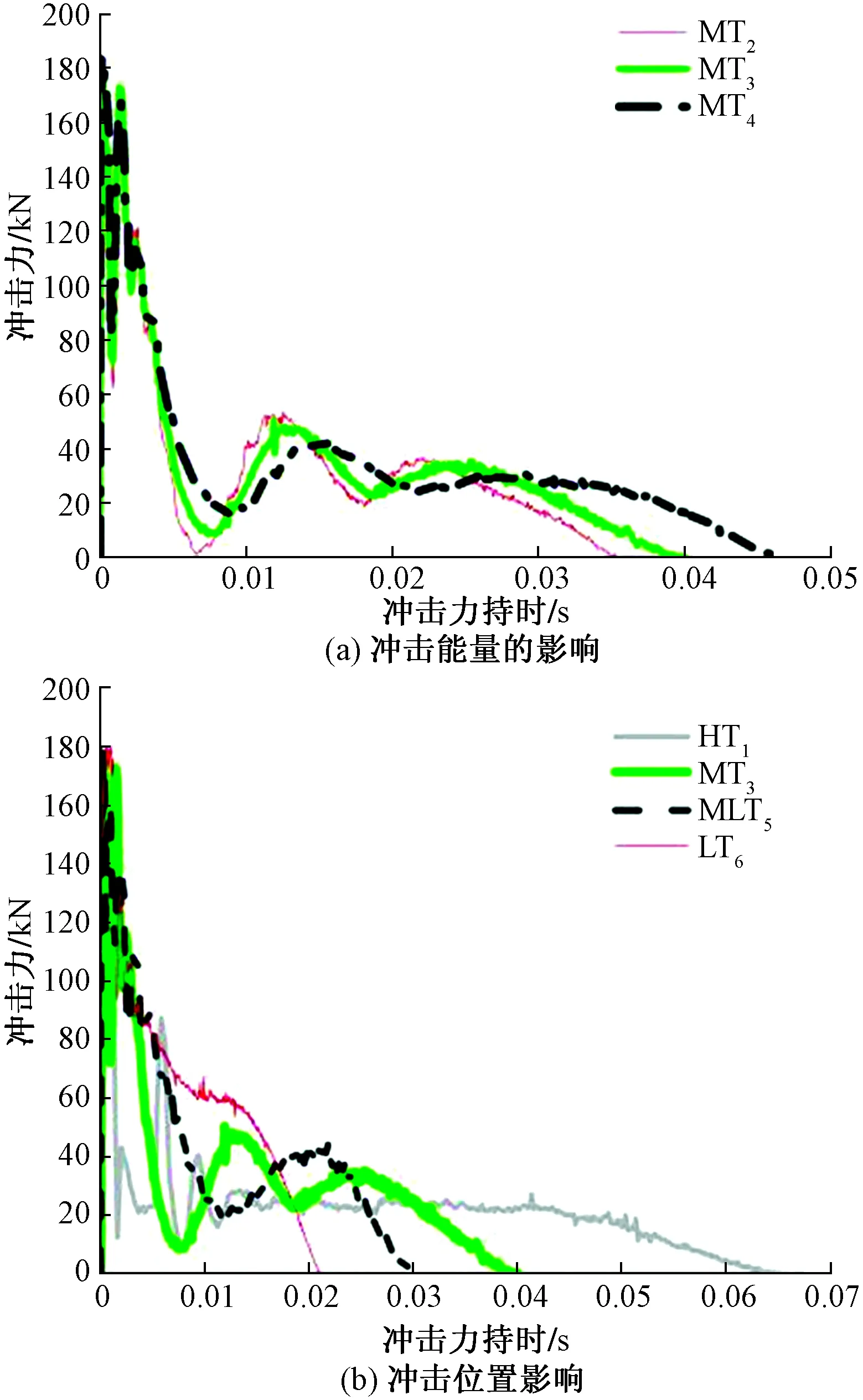
圖6 沖擊時程曲線Fig.6 Time-history curves of impact force

2.4 影響因素分析

為了更加深入研究沖擊荷載作用下鋼構件的動態響應情況，從試件的沖擊力峰值(Fmax)、沖擊力平臺值(Fstab)、沖擊力持時(Tn)、殘余位移(δ)四個方面出發，分析沖擊點位、沖擊能量對格構式鋼柱的動態響應的影響。

2.4.1 沖擊位置的影響

圖7給出了在不同沖擊高度(H)的懸臂試件HT1、MT3、MLT5、LT6動態響應的變化情況，由圖7所知，隨著沖擊作用位置的提高，沖擊力峰值變化不大，穩定在 177.37～180.6 kN，可認為沖擊位置不對沖擊力峰值產生影響。沖擊力平臺值也作為衡量沖擊力大小的重要指標，隨著落錘沖擊點高度的增加，沖擊力平臺值依次為60.3、35.04、29.79、23.3 kN，呈現不斷減小趨勢。沖擊力作用時間試件的沖擊時間最小為21.06 ms，最大為65 ms，沖擊時間隨著沖擊高度的升高而延長，柱頂殘余位移也隨沖擊高度提高由0.18 mm增長到68.23 mm。由此說明，在作用位置提高的情況下，格構式鋼柱所抵御沖擊的能力越來越小，通過更大的殘余變形進行能量耗散，因而造成更長的作用持續時。

圖7 沖擊位置的影響Fig.7 Influences of impact position

為了進一步分析落錘作用位置對構件動力響應的作用情況，根據文獻[2]中有關沖擊力與靜力的理論關系對格構式鋼柱的抗沖擊能力進行分析。

Feq,1=RFu

(1)

式(1)中：Feq,1為構件的理論等效抗沖擊承載；R為動力放大系數，由有限元模擬確定，當試件的材料尺寸等情況相同時，R為恒定值；Fu為根據靜態分析構件的抗沖擊承載力。

荷載的沖擊為動態過程，其中沖擊力可由實際等效沖擊承載力近似表示為

Feq,2=Ea/δ

(2)

式(2)中：Ea為整個沖擊作用下構件吸收的能量；δ為沖擊位置的殘余變形量。

對于構件的靜態承載力，由于型鋼的塑性性能優異，在受極限荷載時，構件會產生塑性鉸從而形成破壞機構，機構的受力情況如圖8所示，從格構式構件受彎承載力Mu出發來確定靜態下抗沖擊承載力為

Fu=Mu/L

(3)

Mu=γWnf

(4)

式中：Mu為試件靜態抗彎承載力，通過規范GB 50017—2017[14]得出；L為沖擊點距塑性鉸的距離，由于底部綴板位置剛度較大，L從底部長綴板頂端處算起；γ為截面塑性發展系數，查表知γ=1；Wn為凈截面模量根據截面慣性矩確定；f為鋼材的抗拉強度，根據文獻[14]知f=266.88 N/mm。

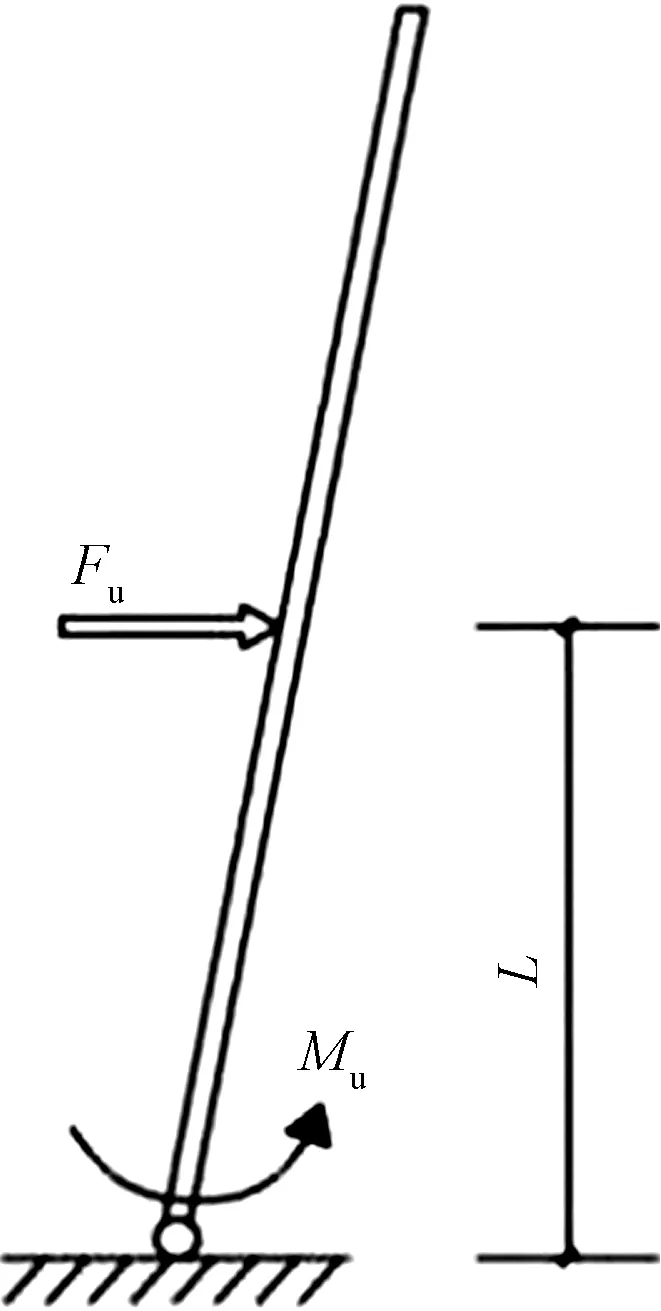
圖8 機構的簡化模型Fig. 8 Simplified model of failed member

將式(1)與式(3)合并得

Feq,1=RMu/L

(5)

式(5)表明試件抗彎承載力對抗沖擊能力的影響關系。計算得受彎承載力Mu=34.04 kN·m，并根據式(1)求得格構式鋼柱的動力放大系數R，具體的計算值如表4所示,為保證安全性，R取最小值1.563。

根據式(5)可得出試件的理論等效抗沖擊抵承載力與位置關系的曲線，并根據式(2)計算出試件HT1、MT3、MLT5的實際等效抗沖擊承載力，由圖9可知，兩者擬合良好，當沖擊位置較高時，試件抗沖擊變形能力較差，但隨著沖擊位置下降，沖擊抵抗力不斷提高，且提高幅度持續加大。但值得注意的是，對于試件LT6，其沖擊能量約3 000 J，吸收能量為2 716.32 J，塑性鉸距離L=0.15 m，沖擊處殘余變形δ=9.52 mm，計算求出的理論等效抗沖擊承載力Feq,1應為345.67 kN，但實際的等效抗沖擊力Feq,2僅為285.33 kN，差值達69.34 kN之多。這是因為當作用位置較低時，由彎曲效應得出的等效抗沖擊承載力較大，在沖擊力保持不變的情況下，不易產生塑性鉸，此時試件變形破壞由抗剪能力決定，其理論等效沖擊承載力為

Feq,1=RVu

(6)

式(6)中：Vu為試件靜力分析下的抗剪承載力。

由于目前未發現針對格構式構件抗剪承載力的計算公式，根據材料力學對格構式鋼柱靜態抗剪承載力進行簡化計算，當落錘對試件LT6沖擊時，作用截面如圖10所示，設沖擊作用方向為y方向，由上文可知綴板與角鋼抗拉強度相近且采用滿焊連接，整體性較好，其抗剪能力主要由格構式鋼柱y方向兩個狹長矩形部分承擔，根據矩形截面切應力強度理論得

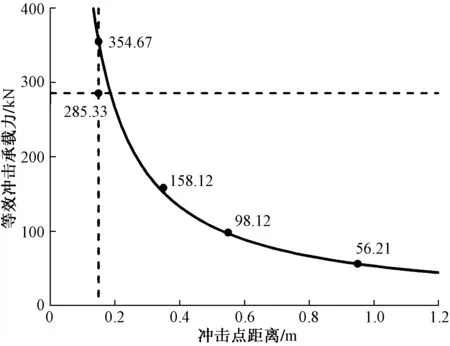
圖9 等效沖擊承載力Fig.9 Equivalent anti-impact capacity

圖10 沖擊截面Fig.10 Cross section of the specimens under impacts

表4 基于有限元模型R的計算值Table 4 Calculation values of R based on finite element models

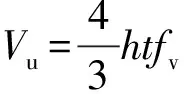
(7)

式(7)中：h為試件截面高度;t為角鋼與綴板厚度;fv為材料抗剪強度，由材料力學第四強度理論fv=0.58f，得出fv=154.79 kN。

計算靜態抗剪承載力Vu=185.75 kN，得出理論等效抗沖擊承載力為Feq,1=RVu=290.32 kN，與實際等效沖擊承載了Feq,2=285.33 kN相比,兩者誤差僅1.7%，證明了計算準確性，并將式(7)擬合，得出懸臂式鋼柱在不同沖擊位置下抗沖擊承載力計算方法。

在本文研究范圍內，隨著懸臂構件沖擊高度下移，試件的抗沖擊承載力加速提高， 等效抗沖擊承載力為

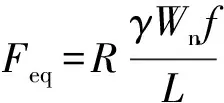
(8)

耐撞性由試件抗彎能力決定，鋼柱根部由于彎曲作用屈曲；當沖擊點下降至較低位置

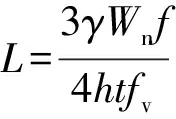
(9)

Mu=Vu，耐撞性由抗剪能力決定， 等效抗沖擊承載力為

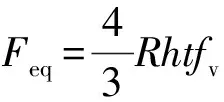
(10)

2.4.2 沖擊能量的影響

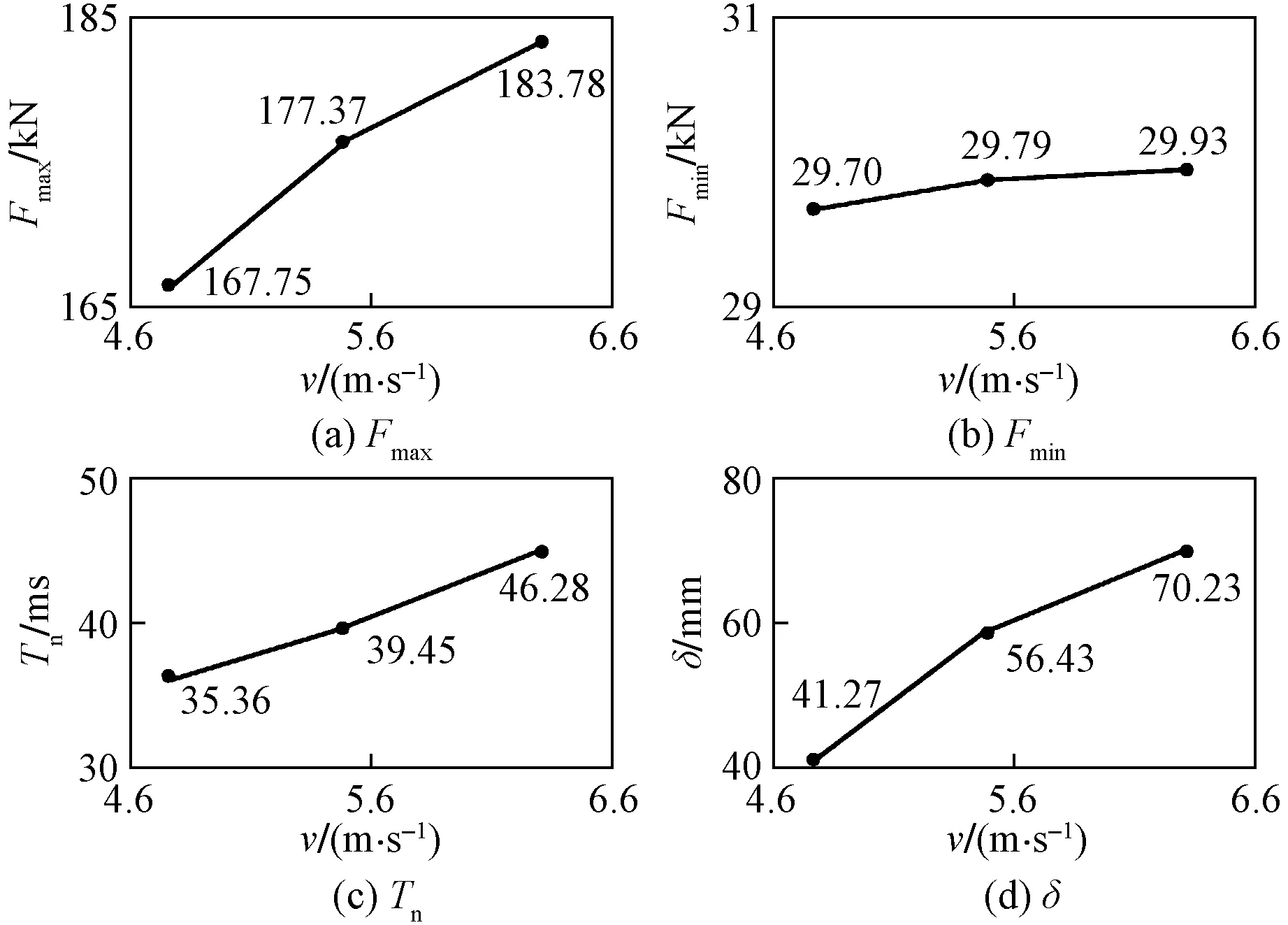
圖11 沖擊速度的影響Fig.11 Influences of impact velocity

通過控制速度來研究沖擊能量對格構式鋼柱動態響應的影響，如圖11所示，對于尺寸與材料性質相同懸臂式的構件MT2、MT3、MT4，沖擊力峰值最小值為167.75 kN,最大值為183.78 kN,隨沖擊速度增加峰值呈增長趨勢。沖擊力平臺值變化不大，穩定在29.7～29.93 kN。隨著沖擊速度增長，沖擊力持時分別為35.36、39.45、46.28 ms，殘余位移分別為41.27、56.42、70.23 mm，沖擊持時與殘余位移均出現明顯的增加。由此可知，隨著落錘下落速度的加大，格構式鋼柱受到的沖擊能量越大，沖擊力峰值越高，沖擊力平臺值基變化不明顯，格構式鋼柱通過產生更大變形來抵御落錘的沖擊作用，這與崔娟玲等[11]對不同沖擊速度下的格構式柱的動態響應結論相一致，證明了模擬試驗的有效性。

3 結論

(1)在本文研究范圍內，當沖擊位置較高時，懸臂式格構柱整體變形呈斜直線，其等效抗沖擊承載力為Feq=RγWnf/L柱底因彎曲作用而受壓屈曲。當沖擊位置下降至L=3γWnf/4htfv以下，懸臂式格構柱整體變形呈折線，變形破壞由剪切效應控制，其等效抗沖擊承載力為Feq=4Rhtfv/3。

(2)當沖擊點較低時，懸臂式格構柱與兩端簡支約束的試件的沖擊力時程曲線相似，均經歷了峰值階段、平臺值階段、卸荷階段三個階段，但當沖擊位置提高時，懸臂式構件會產生二次峰值段，并且作用程度會隨著沖擊高度增加而加劇。格構式鋼柱具有較為穩定的平臺值，但隨著沖擊能量的提高，沖擊力峰值與沖擊力持時明顯增大。

(3)當沖擊能量不變時，提高沖擊位置，試件的抗沖擊能力減弱，將通過更大的變形進行能量耗散，并導致沖擊力持時延長。