基于計算流體力學的空中回收錐套氣動特性分析

趙 航， 廖 鵬， 姚磊江

(1.西北工業大學無人機特種技術國防科技重點實驗室， 西安 710072； 2.西北工業大學航空學院， 西安 710072)

為了擴大作戰半徑，近年來空中發射和回收成為了航空界研究的熱點。載機攜帶多架無人機在空中發射，當無人機完成任務后，載機對其進行回收。空中回收目前仍處于論證階段，當前的回收方式主要有兩種，一種是無人機飛至載機艙門處，用機械臂抓取回收，一種是載機伸出一套繩索-錐套拖曳系統，當無人機與錐套對接成功后，拖曳回收。但考慮到艙門附近復雜的尾流場，不利于機械臂的抓取，優先采用第二種回收方式。Dynetics公司“小精靈”系統的首次真實試驗將在2019年下半年進行，屆時C-130運輸機將在30 min內回收4架無人機。Dynetics公司發射和回收系統最引人注目的特征是類似于空中加油錐形管的回收系統[1]。該回收系統由繩索和錐套組成，無人機頭部安裝一個插頭，在飛控系統的導引下漸漸抵近錐套，插入并鎖緊，然后繩索拖曳錐套和無人機系統一起回收。為了提高空中回收的精確性，首先要對錐套的氣動阻力特性充分掌握。

此前的錐套都用于空中加油系統中，國內外一些學者通過風洞實驗得出了錐套的阻力系數，并進行了數學擬合。Kapseong等[2]提出了一種錐套模型，并進行了風洞實驗，然后通過數學擬合得出了錐套阻力系數的計算公式；NASA德萊頓飛行研究中心Vachon等[3]研究了兩種不同的錐套模型，并且分別經過風洞實驗得出了它們的阻力系數。雖然得到的數據結果可靠性很高，但是風洞實驗需要花費大量的時間和金錢，并在前期投入較大精力準備實驗。采用計算流體力學(CFD)進行數值模擬，可以較為快捷地得出錐套的阻力系數，而且與風洞的實驗結果相差不大。Hayashibara等[4]分別建立了3D和2D錐套模型，用CFD計算了升力系數和阻力系數，并與風洞實驗結果進行對比，結果表明誤差在允許范圍內。程小芩等[5]研究了軟式空中加油的錐套氣動特性；石超等[6]通過CFD計算了不同支柱數對錐套阻力系數的研究并進行了數學擬合。此外還有學者根據錐套阻力特性，進行了空中加油軟管錐套系統的動力學仿真,得出了錐套穩定的區域[7-8]。

上述學者都是基于空中加油這一背景研究錐套的氣動特性，而且只關注了支撐臂支柱數對錐套阻力系數的影響。空中回收過程不同于空中加油，對錐套的氣動特性有著特殊的要求，所以僅僅借用空中加油的錐套的氣動特性是遠遠不夠的。本文針對空中繩索-錐套拖曳回收這一當下熱點為背景，根據其對錐套的特殊要求，建立了不同構型錐套模型并考慮了空中回收時不同的氣流條件，對錐套氣動特性進行了數值仿真研究。

1 錐套三維模型的建立

選取錐套原型如圖1所示。錐套主要組成部分是支柱和前方的穩定傘。

圖1 錐套原型Fig.1 Drogue prototype

圖2 錐套三視圖Fig.2 Drogue set diagram

在CATIA中建立了錐套的三維簡圖(圖2)，為了簡化計算，去掉了錐套的網面，只保留支柱，穩定傘和頭部與拖曳繩索連接的裝置。

2 CFD計算

2.1 網格劃分

選擇CFD計算前處理軟件ICEM對錐套的網格進行劃分，考慮到錐套結構的復雜性，在計算域中選擇Octree八叉樹方法生成非結構網格。網格數量越多，對計算機配置要求更高，計算時間更長，計算結構更精確，考慮到錐套的外形尺寸，經過反復調整，最終選擇錐套的網格數量在300萬～400萬。計算域選擇長12 m、寬8 m、高8 m的長方體區域。計算域網格劃分如圖3所示。

圖3 錐套網格劃分示意圖Fig.3 Diagram of grid division of drogue

2.2 計算方法

2.2.1 湍流模型

選擇SSTk-ω模型，近壁面利用k-ω模型的魯棒性，捕捉黏性底層的信息，可以更加清晰模擬錐套壁面附近的流場。

(2)設置材料屬性：選擇理想氣體，密度為1.225 kg/m3,黏性采用默認選項。

(3)邊界條件：入口條件為速度入口，出口條件選擇自由出流，壁面設置為滑移壁面。

(4)差分格式選擇：采用coupled算法，湍流動能、湍流耗散率均采用二階迎風格式迭代3 000步左右，殘差小于10-4。

2.3 計算結果

假設來流的速度方向沿著錐套的中軸線，速度大小為60 m/s，錐套的流線圖和渦量圖如圖4、圖5所示。

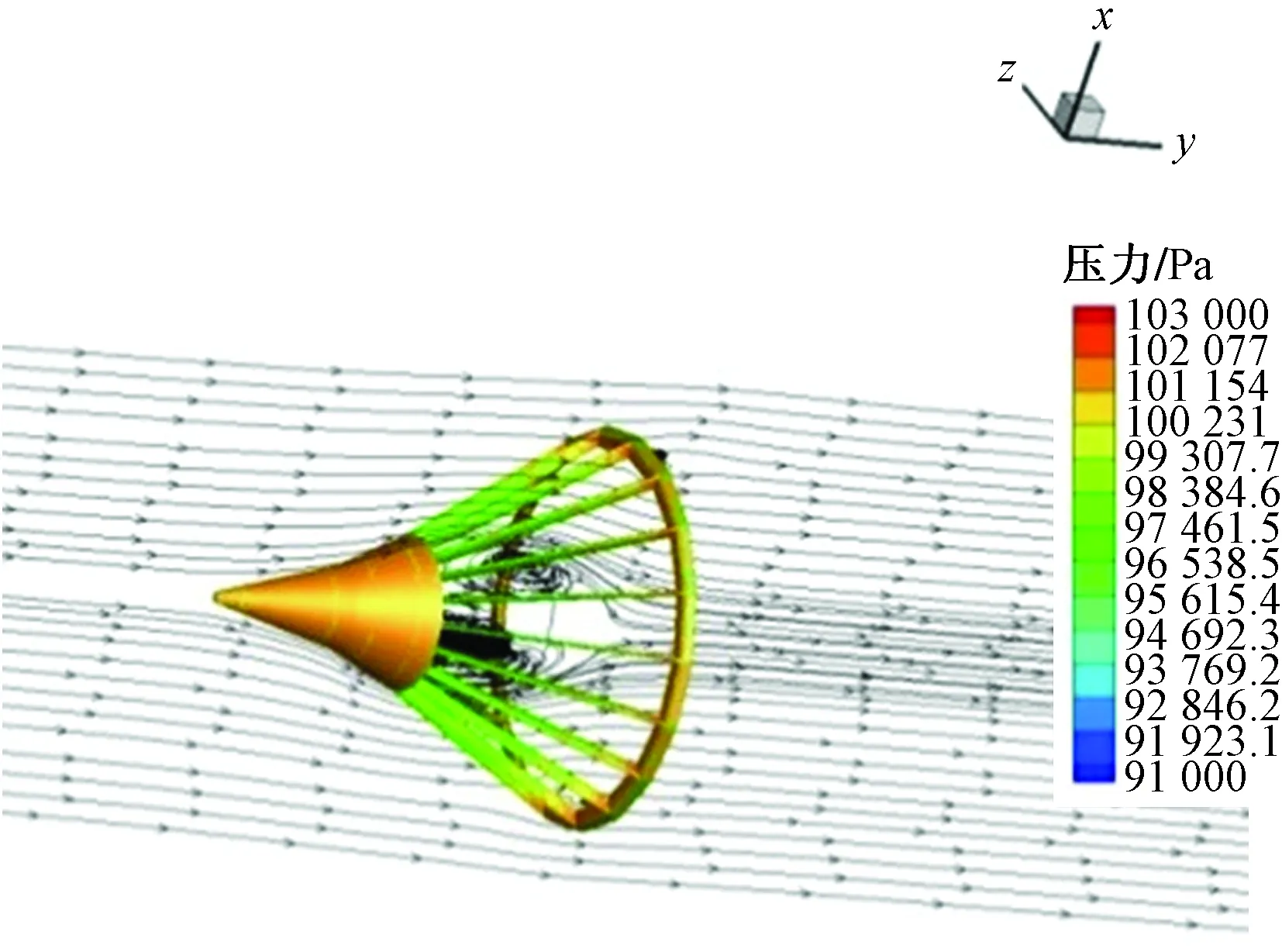
圖4 錐套流線圖Fig.4 Diagram of the streamline of drogue

圖5 錐套渦量圖Fig.5 diagram of the vortex of drogue

從流線圖(圖4)中可以看出穩定傘與錐套頭部的空間內存在明顯的回流區，從渦量圖(圖5)中可以看出支柱和穩定傘附近的渦量較強，符合理論分析。

經計算18支柱的錐套平均阻力系數為1.185，風洞實驗得到的阻力系數平均值為1.13，所以相對誤差4.86%。誤差的來源是三維建模誤差。相對誤差較小，表明了CFD數值計算的準確性。

交流時最好讓老人帶好義齒，喝口水，調整一下體位和呼吸后再進行交流。當然是否飲水也要考慮身體疾病狀況，心力衰竭、腎衰竭有飲水限制時除外。需要提醒的是，康復訓練中的口腔運動以及語言功對于改變口腔功能、語言功能是有效的。

3 仿真算例以及結果分析

采用繩索-錐套系統的空中拖曳回收方式，要保證在無人機與錐套對接之前，錐套系統的穩定性，而阻力是影響錐套系統在來流方向穩定性的重要因素。因此著重討論錐套的不同構型以及不同來流條件對其阻力系數的影響。

3.1 支柱數量對阻力系數的影響

根據理論分析，錐套的阻力主要來源于與支柱連接的穩定傘。穩定傘面積越大，錐套的阻力系數越大。為了確定錐套阻力的主要來源，首先建立了無穩定傘錐套模型如圖6所示，接著計算了支柱數為12、18、24、30的沒有穩定傘的錐套的阻力系數。結果如表1所示。

圖6 無穩定傘錐套Fig.6 Drogue without canopy

表1 無穩定傘錐套支柱數量與阻力系數Table 1 The number of pillar and drag coefficient ofdrogue without canopy

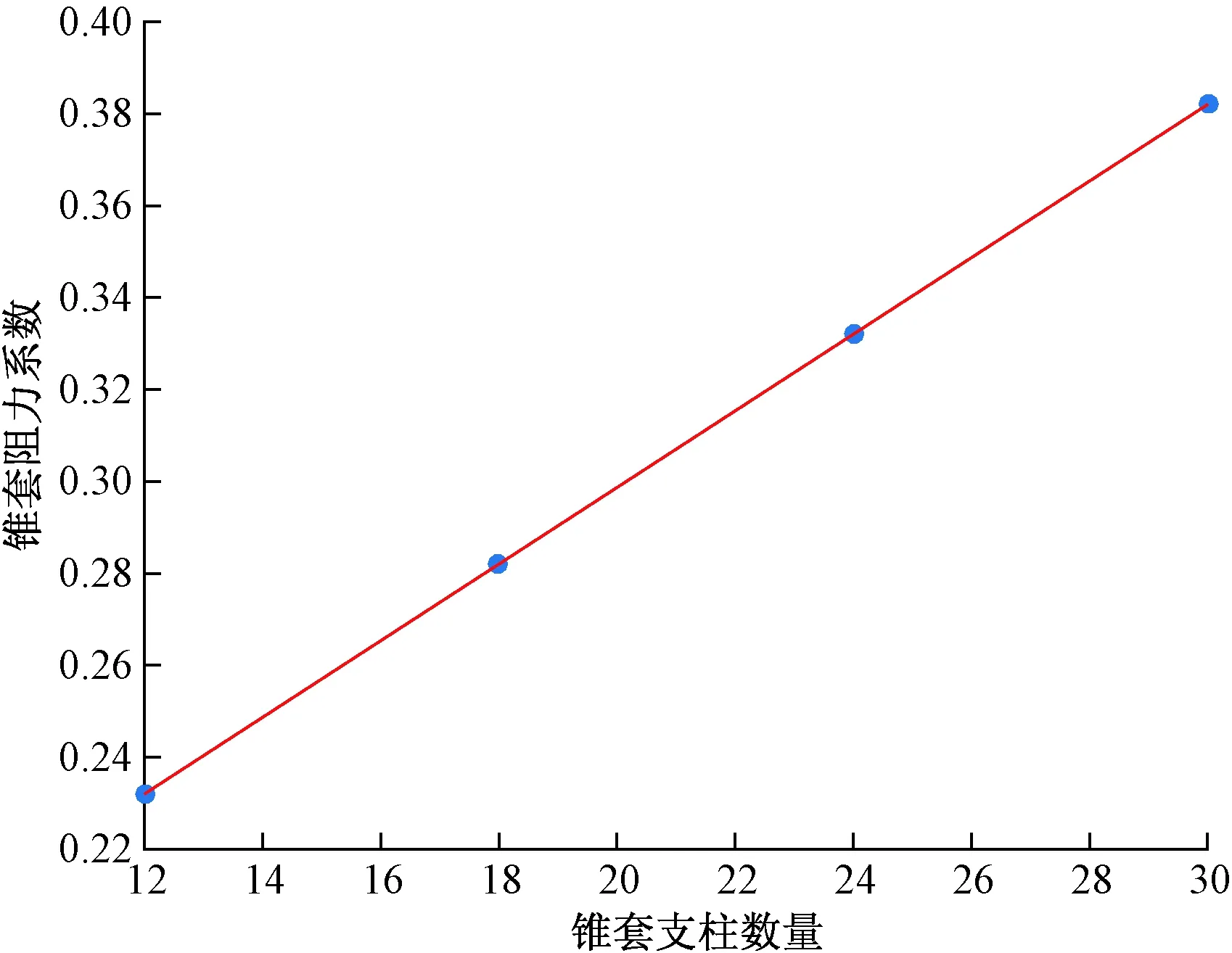
圖7 無傘面錐套阻力系數與支柱數的關系Fig.7 The number of pillar and drag coefficient of drogue without canopy

經過數學擬合分析，可以近似認為無穩定傘錐套的阻力系數與錐套支柱數量(N)線性相關：

Cd=0.008 3N+0.132 0

(1)

接著選取支柱數為12、18、24有穩定傘的錐套分別進行CFD計算，得出它們的阻力系數如表2所示。

表2 有穩定傘錐套支柱數量與阻力系數Table 2 The number of pillar and drag coefficient ofdrogue with canopy

比較支柱數為18和24的有穩定傘和無穩定傘的阻力系數發現，對于無穩定傘錐套，每多兩個支柱，阻力系數增加為0.016 6；有穩定傘錐套，每多兩個支柱，傘面面積減小11.1%，阻力系數減小0.098，雖然增加支柱數在一定程度上增加了阻力系數，但是增加的阻力系數無法彌補因穩定傘面積減小而造成的阻力系數的損失，因此穩定傘是錐套阻力的主要來源，錐套阻力系數隨著支柱數的增加，總體上呈現下降趨勢。

空中回收中，若選擇支柱數量越多的錐套，雖然錐套的結構會更加穩定，但是阻力系數更小，在空中的穩定性較差，當無人機接近錐套時，錐套會出現上下擺動的甩鞭現象[9]，對空中回收對接階段所要求的精確性提出了挑戰，增加了對接時間。若選擇支柱數量較少的錐套，雖然增加了阻力系數，抑制了甩鞭現象，但是錐套的結構不穩定，傘面易損。因此，需要根據實際情況，選擇支柱數量合適的錐套。

3.2 來流速度對阻力系數的影響

圖8 阻力系數與來流速度的關系Fig.8 Drag coefficient curve of drogue with various airspeed

從仿真結果可以看出，改變來流速度對錐套阻力系數影響不大，阻力系數只與錐套自身結構有關，與外界條件關系不大。在空中回收過程中，載機打開尾倉伸出錐套，無論來流速度如何變化，錐套自身的阻力幾乎恒定。因此只需考慮無人機與錐套的對接速度，避免對接速度過大而產生的甩鞭現象，使其安全對接。

3.3 來流迎角對阻力系數的影響

空中回收錐套位于載機尾流場中，實際上是一個非定常流場，不同時刻錐套相對于來流的迎角是不同的，而當無人機與錐套接近時，也會造成錐套的甩鞭現象。總之錐套在尾流場中一直處于擺動狀態，科研人員設計了控制器抑制其擺動[10],因此有必要討論不同來流迎角對錐套阻力系數的影響。

定義來流迎角為來流與錐套軸線之間的夾角，圖9給出了5°迎角和10°迎角的流線圖。

圖9 流線圖Fig.9 Streamline diagram of different angle of attack

表3是不同迎角對應的錐套阻力系數。

表3 不同迎角對應的錐套阻力系數Table 3 Drag coefficient of drogue with variousangle of attack

從圖9可以看出，當迎角增加時，氣流會繞過穩定傘，穩定傘的迎風面積會減小，因此錐套的阻力系數會減小。迎角越大，錐套損失的阻力系數越大，錐套受力的改變會傳遞到繩索上，在來流的影響下繩索會發生抖動，使繩索-錐套系統不穩定導致回收失敗。因此有必要設計錐套運動主動控制系統，實現錐套支柱的張合，改變錐套受力，使整個系統穩定[10-11]。

3.4 支柱展開角對阻力系數的影響

繩索-錐套系統對無人機進行空中回收，當對接成功后，無人機頭部的捕獲桿插入錐套中，無人機的部分機身會隨之進入錐套。當回收不同機身直徑的無人機時，需要選擇展開角不同的錐套，因此有必要討論錐套不同支柱展開角對其阻力系數的影響。在仿真中選擇了支柱數為18，展開角為15°、30°、45°討論不同支柱展開角對錐套阻力系數的影響。其中支柱展開角的定義如圖10所示。

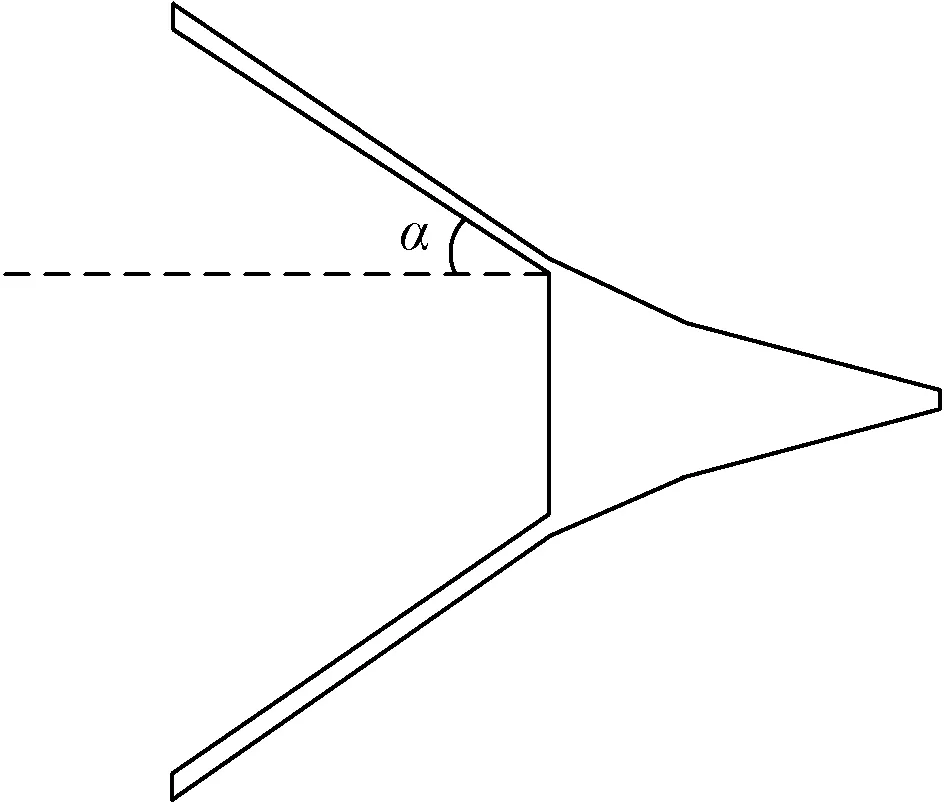
圖10 支柱展開角示意圖Fig.10 Diagram of expansion angle of pillar

圖11～圖13給出不同支柱展開角的流線圖和渦量圖。

圖11 15°展開角流量圖及渦量圖Fig.11 15° expansion angle of pillar

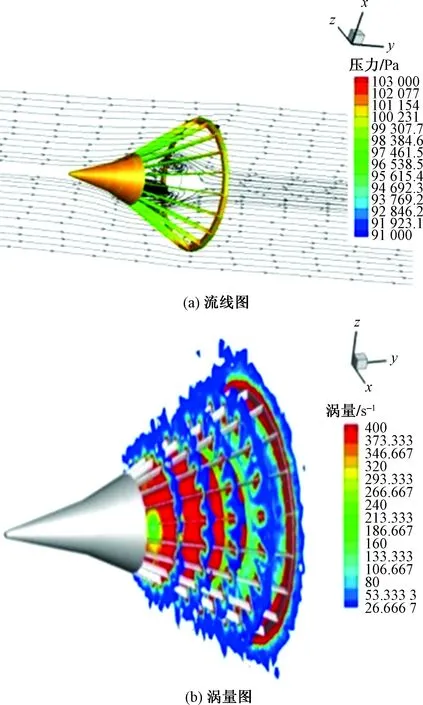
圖12 30°展開角流量圖及渦量圖Fig.12 30° expansion angle of pillar

圖13 45°展開角流量及渦量圖Fig.13 45° expansion angle of pillar

從流線圖[圖11(a)、圖12(a)、圖13(a)]中可以看出，隨著展開角的增加，引流變得順暢，錐套內部回流區逐漸減小。支柱處和穩定傘傘面處的壓力增加，支柱會分散一部分錐套頭部的壓力。在錐套的支柱和穩定傘處存在較強的渦量，展開角越大，穩定傘面附近渦量越大。表4給出了支柱不同展開角與錐套阻力系數的關系。

表4 不同展開角錐套的阻力系數Table 4 Drag coefficient of drogue with variousexpansion angle of pillar

由表4中可知，隨著支柱展開角的增加，錐套阻力系數增加。因為支柱展開角增大會導致支柱迎風面積以及穩定傘面積的增加，但是通過之前的分析，錐套的阻力主要來源于錐套的穩定傘，因此錐套的阻力系數增加。阻力增大，有利于錐套在來流方向保持穩定，減小無人機接近時對其的沖擊影響，不過支柱展開角增大，會使錐套結構承受更大的載荷，要選擇承載能力更強的材料。因此在空中回收選擇錐套時需要根據無人機的機身直徑選擇合適支柱展開角的錐套。

4 結論

(1)采用CFD數值模擬的方法，結合空中繩索-錐套拖曳回收這一背景，研究了錐套不同支柱數量，不同支柱展開角以及不同來流條件對錐套氣動特性的影響。通過與實驗對比可知：CFD計算與風洞實驗相對誤差在可以接受范圍內，因此可以采用CFD計算錐套的氣動阻力。由計算結果可以得出以下結論：首先通過對比沒有穩定傘錐套和有穩定傘錐套的阻力系數得出，錐套的阻力主要來源是穩定傘。穩定傘面積越大，錐套的阻力系數越大。因為穩定傘呈圓環結構，支柱數的增加會減小穩定傘的面積，所以阻力系數會減小；錐套的阻力與其自身結構有關，因此來流速度不會對錐套的阻力系數產生影響；來流迎角增加，錐套穩定傘相對于來流的迎風面積會減小，因此錐套的阻力系數會減小；錐套支柱的展開角增加，會增加穩定傘的面積，使阻力系數增加。

(2)根據空中回收過程中可能出現一些情況，對錐套的阻力特性進行了分析。錐套阻力系數越大，在來流方向上更穩定，減小了擺動，增加了空中回收的成功率。但有時增加了錐套的阻力系數，會增加結構載荷，導致錐套結構的不穩定，因此需要根據具體回收的飛機特征參數，選擇合適的錐套及材料。