基于壓阻反饋信號納米梁非線性振動控制

孔維旭， 劉燦昌， 萬 磊， 黨 壯， 賀成泰

(山東理工大學交通與車輛工程學院， 淄博 255049)

隨著納米技術的發展，微型化、高靈敏度、穩定性好的納機電系統(nano-electromechanical system，NEMS)器件研究成為近年來科研工作者的熱點。納米梁是納米諧振器、振蕩器、傳感器等納機電系統器件的關鍵承載原件[1-3]。當梁處于納米尺寸時，其振動行為容易從線性區跨越進非線性區，表現出多種非線性特性[5-8]。常用的納米梁直流、交流電壓靜電驅動方式也會產生非線性效應[4]，導致納米梁的振動產生失穩，嚴重制約NEMS器件的工作穩定性。因此，NEMS器件的非線性振動控制研究成為學者們的研究內容之一，具有重要的工程意義。

NEMS器件非線性振動控制方法的研究成為中外學者的研究熱點問題之一。Dumitru等[9]研究了靜電驅動懸臂梁微諧振器的非線性響應，建立了包含靜電力和卡西米爾力的非線性動力學方程，并利用多尺度方法對方程進行了分析。Rhoads等[10]通過提出一種新型的納米梁結構裝置，將諧振器的純參數激勵的優點與梁的簡單幾何結構相結合，提出了交流激勵電壓控制的具有理想響應特性的復雜動力學方程。Shaat等[11]針對納米材料的靜電驅動梁，提出了一種精確的非線性模型，選用Euler-Bernoulli梁作為模擬靜電驅動的納米梁模型，并研究了梁結構和尺寸大小對靜電驅動納米梁固有頻率、非線性動力學的影響。Najar等[12]在考慮了小尺度效應下，研究了在非線性力和直流電壓作用下納米梁的動態響應，納米制動器建模選Euler-Bernoulli懸臂梁，利用Hamilton原理推導出彈性模型中的控制方程和邊界條件。Bornassi等[13]利用Euler-Bernoulli梁建立了納米器件在靜電力和分子間力作用下的運動方程，利用微分求積法求解非線性動力學方程。Younis等[14]應用直接多尺度法研究了一類單極板驅動兩端固支微梁振器的主共振特性，探討了軸向力及中性面變形對于非線性共振頻率的影響，研究了不同參數對于系統幅頻響應的影響Abdel Rahman等[15]用同樣的方法研究了單極板驅動兩端固支梁諧振器的超諧和亞諧振動問題，分了系統的動態分岔特性，指出在某些參數情況下系統可能包含多穩態解情況。

壓阻效應是指當材料受到應力時,其載流子的平均有效質量增加或減小(取決于應力方向、晶體取向和電流方向)，從而電阻率發生改變的現象。壓阻效應一般比電阻應變效應大兩個數量級,被廣泛應用于各種壓阻傳感器[16-18]。基于壓阻效應，可以制作各種應力應變傳感器。常用的壓阻效應半導體材料有硅和鍺的摻雜半導體，其中P型硅的壓阻效應比較明顯。壓阻效應已經被廣泛地應用在各種傳感器的研究工作中，如壓阻傳感器，壓阻壓力傳感器，壓阻式加速度傳感器。對于硅納米結構的壓阻的分析和研究是近年來NEMS研究人員的重要課題，相比N型硅而言，P型單晶硅表現出更大的壓阻效應。納米結構的壓阻效應的研究對于基于壓阻效應工作的傳感器有著十分重要的意義[19]。硅壓阻式壓力傳感器采用先進微型化制作工藝集成硅壓阻膜片作為敏感元件, 利用多晶硅的壓阻效應, 在壓阻膜片上淀積的絕緣層二氧化硅上淀積制備三個多晶硅壓敏電阻, 與壓阻膜片組成惠斯通電橋[20-21]。

本文選用Euler-Bernoulli梁作為物理模型，基于壓阻效應對靜電激勵下的納米梁非線性振動控制進行分析研究，考慮多種因素對納米梁非線性振動的影響。旨在以硅壓阻作為系統振動信號提取與檢測的新型理論方法，利用線性、非線性振動分析方法，對非線性振動系統進行控制，為非線性振動控制提供一種新思路。

1 壓阻效應納米梁非線性振動模型

壓阻效應是指當材料受到外加機械應力時，材料的體電阻率發生變化的材料性能。晶體結構的形變破壞了能帶結構，從而改變了電子遷移率和載流子密度，使材料電阻率或電導發生變化。由半導體電阻理論可知：

ΔR=pσR

(1)

式(1)中:p為縱向壓阻系數；σ為電阻的縱向應力。將胡克定律σ=Eε代入式(1)可以得到：

ΔR=pERhw″

(2)

利用壓阻效應提取振動信號的納米梁振動控制系統如圖1所示。懸臂梁上表面靠近固定端部位粘貼硅壓阻膜片，硅壓阻膜片與外接的三個電阻組成惠斯通電橋電路。納米懸臂梁在交變靜電激勵力作用下產生受迫振動，納米梁根部的硅壓阻膜片阻值發生變化。利用惠斯通電橋電路可以將該信號輸出，經信號放大器放大后，作為控制信號進行振動控制。由于硅壓阻膜片長度較短，忽略硅壓阻膜片隨著納米梁變形時曲率的變化。

圖1 納米梁控制系統示意Fig.1 Nanobeam control system schematic

取R=R1，可以得到惠斯通電橋兩端輸出電壓為

v=0.125pEhUw″

(3)

式(3)中:U為惠斯通電橋供電電壓，h為納米梁高度。

由物理模型可知，系統微分方程可表示為

(4)

納米梁諧振器非線性振動偏微分運動方程和邊界條件為

(5)

式(5)中：E、A、I和ρ分別為納米梁的楊氏模量、橫截面積、截面慣性矩和材料密度；b*是單位長度黏滯阻尼系數；l為納米梁的長度；W是納米梁的寬度；g是納米梁和驅動電極間的距離；K為反饋增益參數；V1和V0為作用于納米梁的直流和交流激勵電壓；Ω*為交流激勵圓頻率；gf為系統反饋增益參數；Γ=(0.125pEh)2。

由于直流電壓V1遠大于交流激勵電壓V0, 忽略高階項, 得到：

(6)

對運動方程和邊界條件進行無量綱化處理，得到無量綱運動方程和邊界條件為

(7)

u(0,t)=u′(0,t)=u(1,t)=u′(1,t)=0

(8)

兩邊同時乘以(1+u)2(1-u)2, 得到:

cos(Ωt)]-k(1-u)2U2u″2

(9)

整理得:

εk(1-u)2U2u″2+C

(10)

式(10)中:C為高階項，可忽略。

2 多尺度方法分析

式(9)為非線性方程, 采用多尺度方法, 設解的形式為

u(z,t,ε)=u0(z,T0,T1)+εu1(z,T0,T1)+…

(11)

比較同次冪的系數, 得到:

(12)

(13)

邊界條件為

(14)

式中：Dn=?/?Tn,n=0,1,2,…，式(12)的近似解為

(15)

3 主共振

在外加電壓載荷激勵下，會出現各種共振現象。現研究激勵頻率接近系統固有頻率一半時納米梁的共振和穩定性。激勵頻率可以寫成：

2Ω=wk+εσ

(16)

式(16)中:σ為調諧參數。

(17)

分離式(17)的虛部和實部，得到：

(18)

(19)

由式(18)、式(19)，可以得到振動系統幅頻響應方程為

(20)

4 主共振數值分析

納米梁振動系統存在多值、分岔和混沌等一系列復雜的非線性特性，這些非線性特性對穩定的納米梁振動系統有特別明顯的影響。結合理論推導和數值模擬兩種方法，分析硅納米梁壓阻效應非線性振動特性。通過幅頻響應方程和相頻響應方程得到納米梁非線性振動控制因素，其中包括納米梁參數、阻尼、激勵電壓和反饋增益參數等。旨在分析硅壓阻反饋信號的納米梁非線性振動及振幅的規律，并且以納米梁一階振動模態為例分析控制參數和系統參數對硅壓阻效應納米梁振動的影響。

表1給出了納米梁物理參數，仿真得到系統非線性振動分析與控制的幅頻響應曲線。圖2給出了交流激勵電壓不同時的幅頻特性響應曲線。當交流激勵電壓幅值等于0.2、0.25 V時，共振頻率點在左區間，在最大振幅點發生跳躍現象，振動響應不穩定。當交流激勵電壓幅值減小至0.1 V時，振動趨于穩定，振動響應曲線向左偏離σ=0軸趨勢減緩。從圖2可以知道，隨著交流激勵電壓幅值增大，最大振幅逐漸增大，幅頻特性響應曲線逐漸向左彎離σ=0軸, 納米梁非線性振動呈現軟彈簧特性。

表1 納米梁物理參數Table 1 Physical parameters of nanobeam

圖2 交流激勵電壓幅值不同時的幅頻響應曲線Fig.2 Amplitude-frequency response curves fordiffevent amplitudes of AC excitation voltage

無量綱阻尼不同時的幅頻特性響應曲線如圖3所示。由圖3得，在遠離共振區間處，改變無量綱阻尼值對振幅影響較小，增大阻尼可以使最大振幅減小。隨著無量綱阻尼的增大，振動響應逐漸趨于穩定，多值區間逐漸減小至消失，最大振幅點與共振頻率點的偏移量逐漸減小，這與實際情況相符。

圖4描述了反饋增益參數K不同時的系統幅頻特性響應曲線。由圖4可得，反饋增益參數對最大振幅影響較小，當頻率遠離共振區域時，反饋增益參數對振幅影響較小。在反饋增益參數逐漸增大的過程中，納米梁非線性振動行為逐漸向軟彈簧特性過渡。當反饋增益參數等于8時，最大振幅點近似在σ=0處得到，納米梁振動呈現線性振動。由圖4及幅頻響應方程可以得到，反饋增益參數是通過改變非線性項的值實現對納米梁非線性振動的控制。因此可以選擇適當的反饋增益參數，實現對納米梁振動的穩態控制。

圖3 無量綱阻尼不同時的幅頻特性曲線Fig.3 Amplitude-frequency curves for different-dimensionless damping coefficient

圖4 反饋增益參數K不同時的幅頻響應曲線Fig.4 Amplitude-frequency curves for different-parameters K of feedback gains

圖5給出了納米梁與極板間初始距離不同時的幅頻特性響應曲線。當初始間距為470、450 nm時，在σ=0的左區間，存在多值區間，系統振動不穩定，由于非線性項的作用，幅頻特性響應曲線向左偏離σ=0軸。由圖5可得，隨著納米梁與極板間距初始距離減小，系統振動響應逐漸趨于穩定，最大振幅減小，曲線向左偏離σ=0軸減緩。

激勵電壓不同時，最大振幅與納米梁長度的關系曲線如圖6所示。由圖6可知，當激勵電壓幅值相同時，最大振幅隨著納米梁長度的增加而增加。且當納米梁長度相同時，最大振幅隨著激勵電壓幅值的增加而增加。當系統阻尼不同時，最大振幅與納米梁長度的關系曲線由圖7所示。由圖7可知，阻尼相同時，最大振幅與納米梁長度正相關，且當納米梁長度相同時，最大振幅與阻尼值同樣正相關。

圖5 梁與極板距離不同時的幅頻響應曲線Fig.5 Amplitude-frequency response curves when the initial distance between nanobeam and plate is different

圖6 交流激勵電壓幅值不同時最大振幅隨納米梁長度變化曲線Fig.6 The maximum amplitude of the AC excitation voltage amplitude is different from that of the nanobeam

圖7 阻尼不同時最大振幅隨納米梁長度變化曲線Fig.7 Curves of maximum amplitude with nanometer beam length when damping is different from that of the nanobeam

反饋增益參數不同時臨界電壓與納米梁長度的關系曲線如圖8所示。由圖8可知，反饋增益參數相同時，臨界電壓與納米梁長度負相關。當納米梁長度相同時，臨界電壓與反饋增益參數負相關。

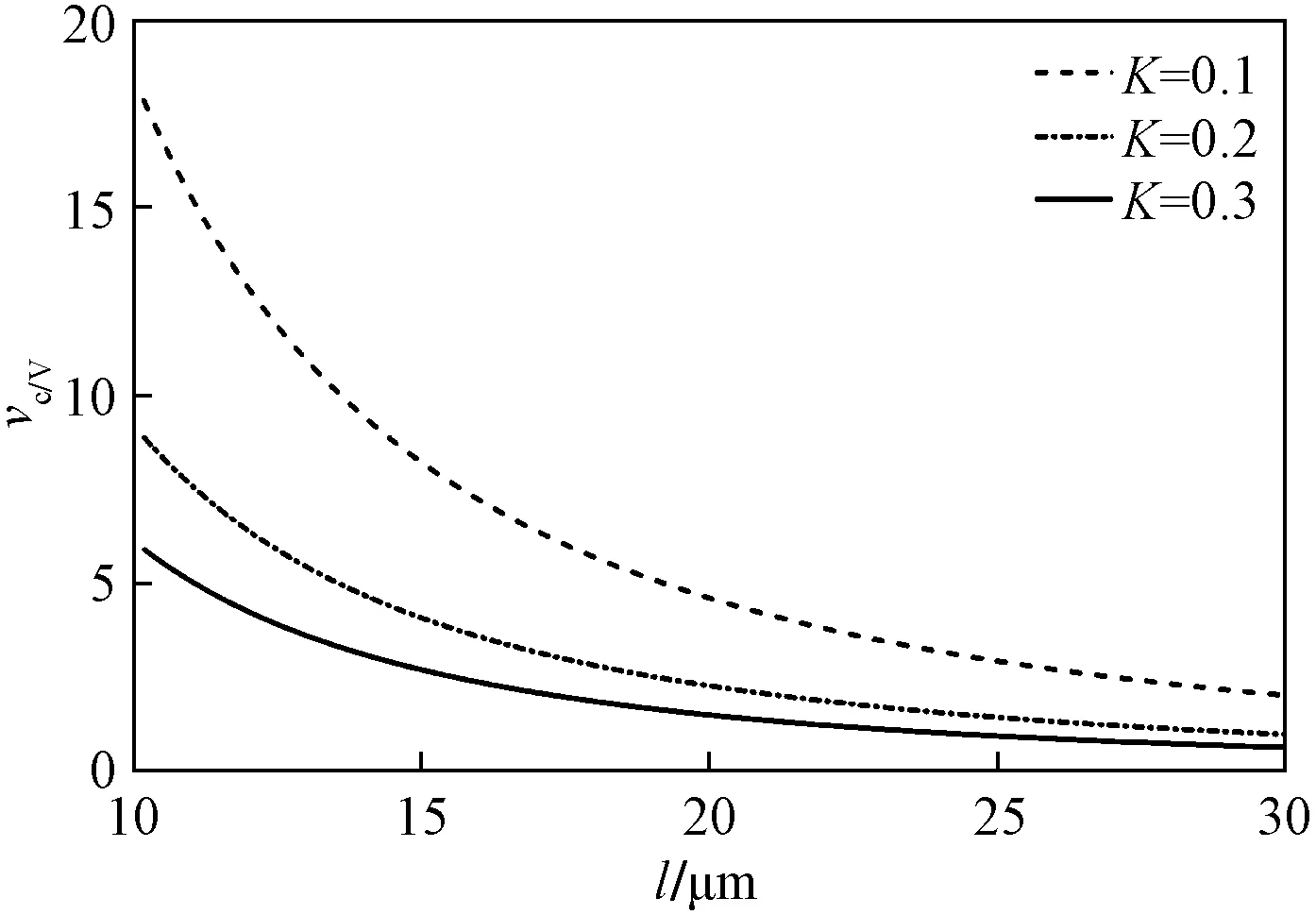
圖8 反饋增益參數不同時臨界電壓隨納米梁長度變化曲線Fig.8 Curves of critical voltage as a function of nanobeam length when feedback gain parameters are different from that of the nanobeam

結合圖2～圖5，通過交流激勵電壓、無量綱阻尼、反饋增益參數和梁到極板距離能夠得到非線性微分方程里非線性項的大小。通過改變以上幾個參數，可以改變非線性項數值大小，繼而控制和降低納米梁振動系統的非線性。當交流激勵電壓從0.25 V降到0.1 V時，系統的非線性減小約60%左右。當無量綱阻尼從0.058 5增大至0.087 8時，系統的非線性減弱40%左右。增大反饋增益參數或減小梁與極板距離，能夠使系統的非線性振動逐漸趨于穩定。圖6～圖8分別反映了交流激勵電壓幅值、阻尼值和反饋增益參數與納米梁長度的關系。

5 近似解和數值解對比結果

為了使論證結果具有正確性和客觀性，在近似解法的基礎上，進一步算出了數值解，從而可以根據兩種解法進行對照。

令u=φ(x)q(t)，由式(10)可以得到：

(21)

(22)

根據式(21)、式(22)，通過程序可以得到數值解結果。以交流激勵電壓0.1 V和0.2 V時的近似解幅頻響應曲線為例，將數值解圖像繪制在近似解幅頻特性曲線圖上，其對比結果如圖9所示。總體來說兩種曲線符合情況較好，近似解與數值解客觀誤差必然存在，但是，微小誤差對總體結果的影響可以忽略。兩種計算結果良好的貼合性，說明本文近似計算解法具有合理性和客觀性。

圖9 近似解(MMS)和數值解(LTI)運算結果對比Fig.9 Approximate solution (MMS) and numerical solution (LTI) operation result comparison chart from that of the nanobeam

6 結論

(1)通過加載交流激勵電壓控制納米梁振動，硅壓阻膜片阻值隨納米梁振動發生變化，利用這種阻值變化作為反饋信號來控制納米梁非線性振動。這種方法可以較好地控制納米梁的非線性振動行為。根據近似計算結果，可以得到交流激勵電壓、無量綱阻尼、反饋增益參數和極板與納米梁間距的幅頻響應關系曲線圖。

(2)交流激勵電壓、無量綱阻尼、反饋增益參數和梁到極板距離能夠改變非線性項數值大小，繼而控制和降低納米梁振動系統的非線性。當交流激勵電壓從0.25 V降到0.1 V時, 系統的非線性減小約60%。當無量綱阻尼從0.058 5增大至0.087 8時，系統的非線性減弱約40%。增大反饋增益參數或減小梁與極板距離，能夠使系統非線性振動逐漸趨于穩定。

(3)臨界電壓與反饋增益參數負相關。最大振幅與阻尼負相關，但是最大振幅與激勵電壓正相關。為了使非線性振動趨于穩定，根據研究結果對各參數進行調整，可以得到較好的控制效果。