繞射波探測淺層空洞的正演模擬與成像初探

張燕生　陸金波

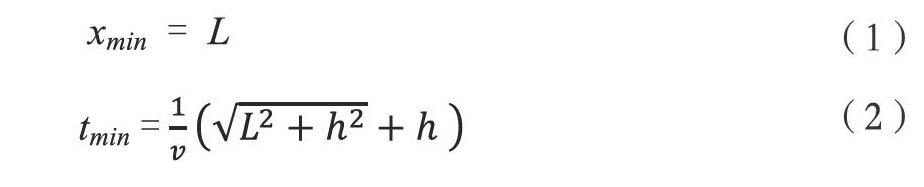
摘 要：利用傳統的反射波地震勘探分辨率很難滿足小尺度淺層地下空洞的探測需求，地震產生的繞射波卻因其特有的傳播特性，使得發現淺層地下空間中存在的小尺度異常成為可能。本文通過建立淺層地下空洞地質模型并進行地震波場正演分析，闡明繞射波能夠對埋深20 m 至50 m、異常尺度為2 m的空洞進行有效的刻畫成像，從而說明，在地下工程（隧道、管線等）建設過程中，可以通過合理布設地震觀測系統，運用繞射波地震勘探方法對淺層地下空洞進行較好地探測，提高城市建設的安全性。

關鍵詞：繞射波;空洞異常;淺層勘探;地下空間;地下工程

Abstract： It is difficult to meet the needs of small-scale underground cavity detection for the resolution of the classical reflection seismology. However， diffractions generated from seismic wave propagation procedure would be more properly to detect the small-scale anomalies in the shallow underground space due to their unique propagation characteristics. This paper states that diffractions can effectively imagine the cavity with an abnormal size of 2m in the depth of about 20 m to 50 m， through modeling the near subsurface cavity and forwarding seismic wave. The forward modelling results show that diffraction wave can effectively describe the cavity with an abnormal size of 2 m in the buried depth of 20 m to 50 m. It shows that the diffractions exploration method is much benefit to detect shallow cavity by certain suitable seismic survey system in those city underground engineering （tunnel， pipeline， etc.） projects， even then guarantee the safety of urban construction.

Keywords： diffractions; cavity anomalies; shallow survey; underground space; underground engineering

0 引言

城鎮化進程的加速，促使地下工程（隧道、管道等）建設不斷增加。淺層地下空洞（灰巖溶洞、水流沖刷形成的涵洞或地下坍塌等）成為地下工程施工探測中的難點，制約了城市建設施工安全。因此，查明地下空洞分布情況是保障地下工程建設安全的重要任務。傳統探地雷達能夠有效探測地下3 m 至5 m 的脫空，但對于埋深十幾米至幾十米以下的空洞或涵洞無法探測。電法勘探探測深度較大，但分辨率差，無法滿足對小尺度的空洞探測精度的要求。

淺層反射波地震勘探在城市地質勘查、水利工程勘查及巖土工程勘查工作中逐漸普及（金維民等，2004;蔣維平等，2008;吳怡等，2006），該方法震源能量小，對周圍環境無明顯破壞，同時勘探精度相對較高。但隨著工程勘探精度要求的提高，想要辨識灰巖地層中2m尺度的空洞，利用淺層地震勘探很難獲得較好的探測效果。從地震勘探理論出發，地震勘探縱向上分辨率為1/4波長。要識別2 m異常，則要求波長不能低于8 m，灰巖溶洞的地層速度以2400 m/s計算，則地震勘探的主頻需達到300 Hz以上，該頻率在現階段反射波地震勘探中難以實現。對于橫向分辨率而言，要識別2 m尺度的異常，亦極為困難。

地震波在經過地下小尺度斷層、尖滅或孔洞時，會產生繞射波。繞射波在地震波場中與反射波具有特征差異，繞射波具有超分辨率能力，即繞射波能夠識別小于地震波長異常體的能力。地質勘查領域中地震技術應用不斷深入，繞射波的作用不斷得到重視（Khaidukove et al.，2004;Bansal et al.，2005;Moser et al.，2008），物理模型和波場計算方面成果顯著。同時，繞射波成像技術也得到較好的發展（李正偉等，2018;黃建平等，2012;劉玉金等，2013），進一步推動了繞射波在地震勘探中的應用。本文在前人對繞射波理論研究的基礎上，對溶洞或其他地下空洞發育的地質模型進行地震波場正演，分析繞射波在相應地質特征下對淺層空洞的識別能力。

1 繞射波勘探原理

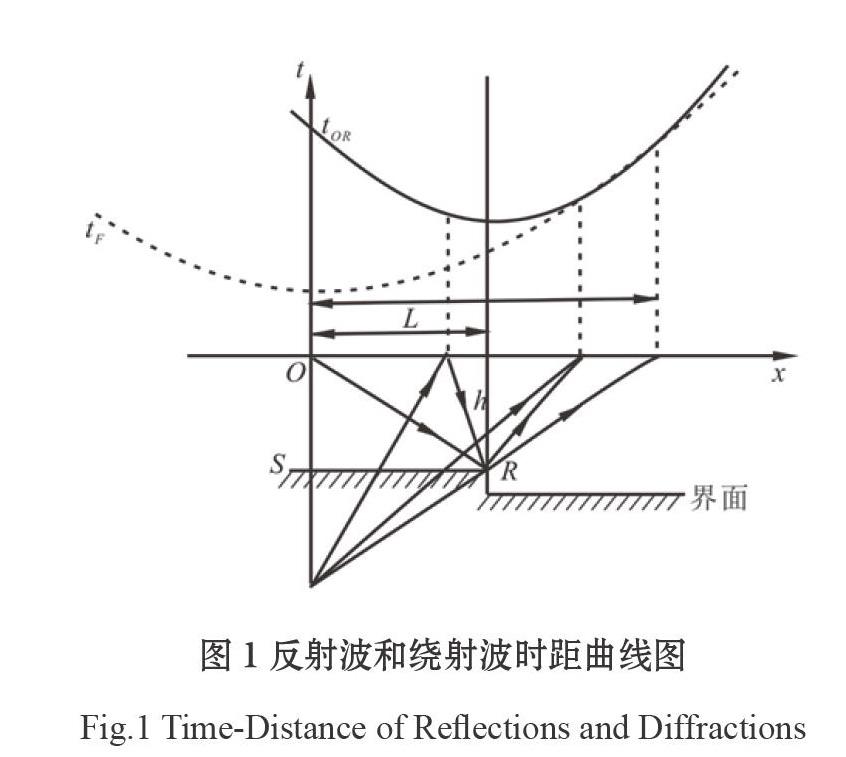
地震波在地層中傳播時，遇到小尺度（小于波長）異常體或巖性突變點，這些異常點會成為新的震源，發出子波向周圍傳播。這些新產生的波成為地震繞射波（陸基孟等，2011）。以斷棱產生的繞射波為例說明繞射波與反射波的時距曲線差異。

圖1中反射界面S中間發育斷棱R，地震波傳播到R點處出現繞射波。測線OX與斷棱垂直，激發點位于O點。地震波從O點發出，傳播到R點后，以R點為中心（R點為虛震源）產生繞射波，被測線上個接收道接收。其中虛線為tF為O點震源激發，反射界面RS的反射波時距曲線;tR為O點激發R點產生繞射波的時距曲線。推導過程在文獻中有詳細說明。繞射波的時距曲線也可以變換為標準雙曲線方程。當測線與斷棱垂直的情況下，繞射波時距曲線的極小點xmin位于繞射點的正上方，其對應的極小時間tmin，即：

激發點移動時，繞射波的時距曲線極小點在測線上的位置不變，但時距曲線會沿t軸平移，時距曲線的形態保持不變。利用繞射波時距曲線的這些特點在共炮點地震記錄中能夠較好的識別繞射波。

2 理想地質模型中繞射波特征分析

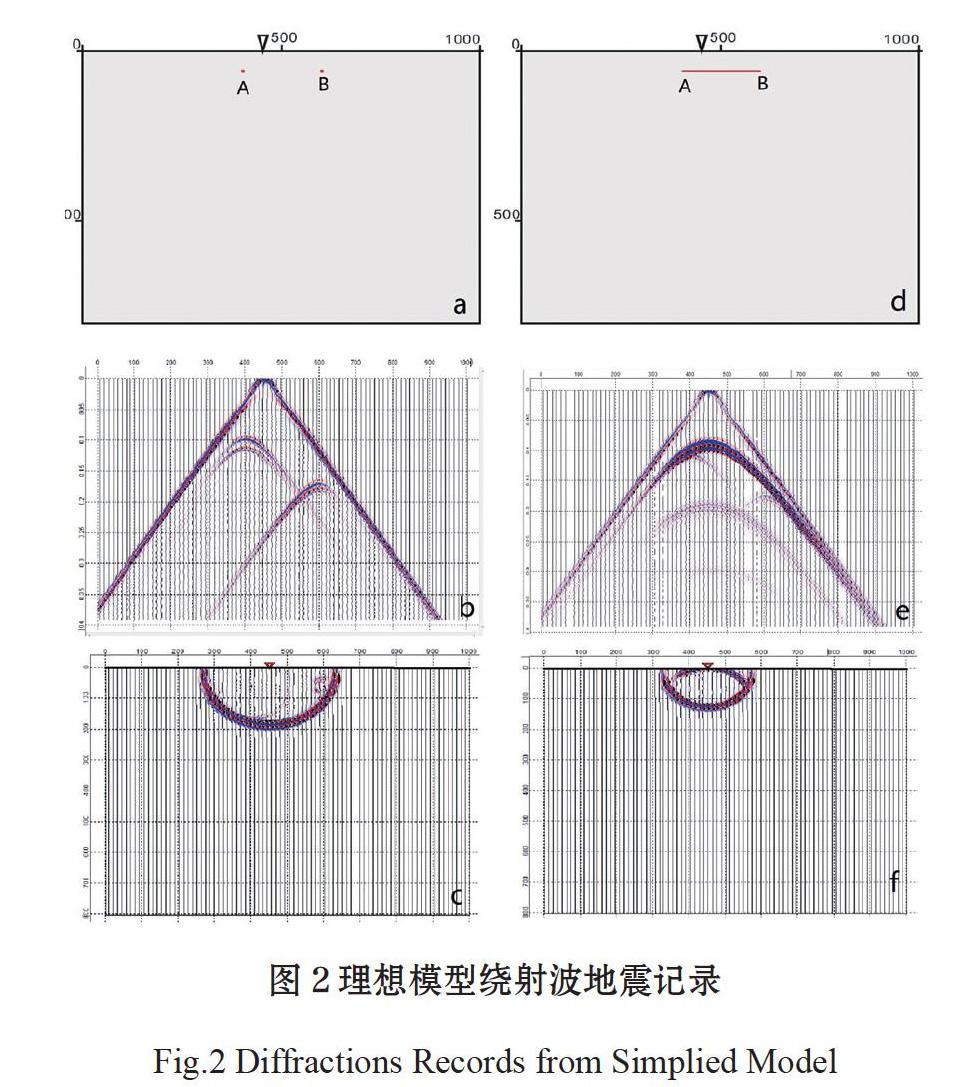
為了能夠識別地層中繞射波地震記錄特征，我們建立了兩個理想的地質模型。模型1如圖2a所示，為水平地表，均質地層，長度1000 m，深度800 m，縱波速度1200 m/s，內部未設計反射界面，震源位置（450，0）點，檢波點位于地表，間隔距離2 m，在A點（400，60）和B點（600，60）兩點設置繞射點，模型中繞射點的尺度設置為2 m。用主頻100 Hz的雷克子波進行正演模擬，介質中地震波長12 m，遠大于繞射點尺度。圖2b是模型1的共炮點道集，道集上顯示3組地震波，分別為直達波和兩個繞射點產生的繞射波。圖中可見繞射波極小點對應地表投影與繞射點對應地表投影位置一致。但兩組繞射波極小點對應的時間不一致，反映出A、B兩點相對震源距離的差異，正如繞射原理所描述，震源相對位置的改變，不改變繞射波組的極小點的位置，只是繞射時距曲線在t軸上移動。由于模型中未設計反射面，同時繞射點尺度遠小于地震波長，不足以產生反射波，因此，正演道集中沒有反射波顯示。該理想狀態下的地質模型，能夠清晰的展示繞射波在共炮點道集下的波組特征，為灰巖溶洞繞射波識別提供模式基礎。圖2c展示的是繞射波產生的波場特征。地震波自震源產生，以球面形式向外擴張，捕獲圖2c的時刻波面已經通過繞射點，以繞射點為中心在波后產生向周圍擴散的繞射波。

模型2如圖2d所示，在模型1的同尺度水平地表地質模型中，將模型1中A、B兩個繞射點進行連線，設置成為一個反射界面，模擬一個理想狀態下不連續沉積的地質模型。根據繞射波產生的條件在該反射界面A、B兩端將產生繞射波。用主頻100 Hz的子波對模型進行正演，震源位置與模型1等同。對該模型進行正演，圖2e為正演的共炮點地震道集。可見，直達波，AB界面反射波、A、B兩個端點產生的繞射波以及層間多次波（干擾波）。繞射與反射波組部分重合，仍可觀察到兩套繞射波組的極小點位置，該位置與模型1兩個繞射點的位置一致。圖2f為該模型正演的波場快照，繞射波以不連續地層斷點為中心向周圍擴散。因此，在單純繞射點地質模型或不連續地層模型中，在炮集上或波場特征上，繞射波與反射波有明顯差異，利用疊前的處理手段在去除多次波的基礎上，采取有效的繞射波分離方法，即可將反射波去除，獲得如模型1一致的繞射剖面，進一步獲得繞射波成像數據。

3 灰巖溶洞地質模型正演

結合灰巖地層發育特征，建立灰巖溶洞地質模型。以武漢地區為例，灰巖地層一般埋深20～50 m，灰巖中縱波速度4500 m/s，上覆地層縱波速度1200 m/s。設計模型長1000 m，深度600 m。灰巖與上覆低速層界面深度50 m，在x=350 m和x=600 m處設計兩個溶洞，溶洞尺度分別為5 m和2 m。溶洞位地層界面下3 m處，內部充滿水。

觀測系統設置。本次正演過程中采用中間放炮，兩邊接受方式。設置51炮，間隔10 m，均勻分布在x=250 m至x=750之間。檢波點設置：間隔2 m，最大偏移距100 m，滾動排列。

研究過程中采用Tesseral 2D全波場正演模擬軟件，該軟件基于射線追蹤和有限差分標量波動方程的簡化算法，能速有效的對復雜地質模型開展正演計算。

正演過程中采用主頻100 Hz雷克子波，對灰巖溶洞地質模型進行正演（圖3）。正演炮集上能夠清晰觀測到兩個溶洞產的繞射波（圖4），說明該地質特征上，能夠利用繞射波對灰巖溶洞進行識別工作。但繞射波能量弱、衰減快，難以在強反射波場中顯示出來，因此，在數據域內進行繞射波信息分離，對繞射波信息進行偏移成像，有助于地質工作者，對灰巖溶洞進行有效刻畫。

4 效果分析

在巖溶地質模型波場正演模擬的基礎上，對道集數據進行偏移成像。在不進行繞射波分離工作情況下，進行傳統的偏移成像，成像結果如圖5a，可見清晰灰巖頂界面反射波組，但溶洞在偏移剖面上沒有反應。如前所述，正演設計中，主頻100 Hz的子波，在v1=1200 m/s和v2=4500 m/s的地層中波長分別為λ1=12 m和λ2=45 m，巖溶尺度（2 m、5 m）小于波長，難以產生有效反射，導致反射波偏移剖面中，巖溶體不可見;在繞射波分離基礎上，對繞射波進行分離成像，成像結果如圖5b。在x=350 m和x=600 m位置下清晰可見巖溶體產生的波組響應。左側波組能量比右側波組能量強，說明巖溶異常體的尺度對波場中產生繞射波的強度有影響，解釋過程中，通過模型分析，能夠建立巖溶體相對尺度關系。

正演試驗過程中對子波的主頻進行替換，結果顯示在理想狀態下（不考慮地震波頻散、高頻衰減、層間多次波），地震勘探采用頻率越高，繞射波對小尺度巖溶異常體的刻畫能力越好，見圖6。但實際勘探過程中，地震頻散、高頻衰減、多次波以及檢波器采樣能力等客觀因素都會對繞射波勘探造成影響。因此，在勘探過程中，需進一步結合實際地質情況，選取合適的觀察系統以及震源、檢波器等，來保證接受數據中獲取有效的繞射波信息。

國內外眾多學者對繞射波的分離與成像有長期大量研究。Landa等（1987）利用相位校正方法，對繞射波在共偏移距剖面上進行目標定位;Nowak等（2004）通過比較波場中繞射波和反射波時距曲線在極小點位置差異，對其曲線進行拉東變換，實現繞射波提取工作;Berkovitch等（2009）利用局部時差校正方程將繞射波時差曲線進行參數化，從而獲取高信噪比繞射波疊加剖面;Asgedom等（2011）修正傳統共反射面元疊加方基礎上，結合相似度分析和多信號分類技術，將繞射波從波場中分離。趙驚濤等（2011）指出共偏移距剖面中振幅主能量及極性反轉出現在繞射點的地面投影處，因此，共偏移距剖面更有利于繞射波的識別與分離。近年來基于反穩相濾波繞射成像技術（劉培君等，2017）、最小二乘自適應濾波的繞射波分析技術（李學良等，2013）不斷出現，繞射波分離與成像技術日趨成熟。

根據繞射波分離過程在整個地震數據處理流程中的階段，總體可分為疊前繞射波分離和疊后繞射波分離。疊前繞射波分離依據繞射波和反射波的波場走時規律及特征差異，相位特征差異，能量特征差異等因素，在成像算子中進行分離成像;疊后繞射波分離成像主要包括優勢傾角濾波法、PWD法（Plane Wave Decomposition，平面波分解）、奇異值分解方法等。

本次繞射波偏移基于kirchhoff積分偏移理論，如下：

這里P（xs， xr， z=0）為地表觀測得到的波場值，p（x， z， t）為反射點（x， z） 處在t時刻的波場值，rs和rr分別代表炮點到反射點、檢波點到反射點的距離，vd和vu分別代表下行波和上行波沿射線路徑的均方根速度或層速度，系數A為保幅處理因子，作為振幅比例因子，實現保幅處理。

5 結論

灰巖巖溶地質條件給地下空間建設施工帶來巨大安全隱患，常規物探方法難以有效的探測到埋深較大的巖溶異常。相對于傳統反射波地震勘探，在提高線道密度的基礎上，利用地震繞射波超分辨率能力，對分離的繞射波進行偏移成像，能夠對灰巖地層中巖溶異常體進行有效的刻畫。正演結果表明，對于埋深50 m，尺度2 m的溶洞，在道集數據上能夠識別到清晰的繞射波，繞射波偏移剖面上，波組能夠正常歸位，顯現巖溶體發育空間位置。同時，正演顯示巖溶體尺度對繞射波能量相關，尺度相對大的巖溶體產生的繞射波能力相對小尺度的巖溶體產生繞射波的能量強，通過這一相對關系，在巖溶體刻畫過程中，根據波組能量關系可以相對獲取巖溶體的相對尺度。總之，在深埋溶洞探測方面，繞射波地震勘探具有切實意義，隨著地震采樣能力的提高以及處理手段的不斷改善，繞射波對灰巖地層小尺度巖溶刻畫能力會不斷提高。

參考文獻：

黃建平， 李振春， 孔雪， 等， 2012. 基于PWD的繞射波波場分離成像方法綜述[J]. 地球物理學進展，27（6）：2499-2510.

金維民， 杜兵建， 2004. 淺層地震勘探在滑坡勘查中應用[J]. 中國煤田地質（S1）：97-99.

蔣維平， 孟憲民， 2008.地震反射波法在淺層勘探中的應用[J]. 中國煤炭地質（9）：59-60+67.

陸基孟，王永剛，2011. 地震勘探原理[M]. 3版.北京：中國石油大學出版社.

李正偉， 張劍鋒， 劉偉， 2018. 基于傾角-偏移距域道集的繞射波成像[J]. 地球物理學報，61（4）：1447-1459.

劉培君， 黃建平， 李振春， 等， 2017. 一種基于反穩相的深度域繞射波分離成像方法[J]. 石油地球物理勘探， 52（5）：967-973+879.

劉玉金， 李振春， 黃建平， 等， 2013. 繞射波疊前時間偏移速度分析及成像[J]. 地球物理學進展，28（6）： 3022-3029.

李學良， 孫晨， 袁義明， 等， 2013. 利用最小二乘自適應濾波實現繞射波分離[J]. 地球物理學進展，28（2）：777-784.

吳怡， 嘉世旭， 段永紅， 等， 2006.地震折射波法在鄭州市西區淺層勘探中的應用[J]. 地震地質（1）：84-92.

趙驚濤， 王真理， 于彩霞， 2011. 地震勘探中的邊緣繞射波及其動力學識別方法[J]. 地球物理學進展，26（1）：194-206.

Asgedom E G， Gelius L J， Austeng A， et al.， 2011. A new approach to post-stack diffraction separation[R]. SEG Expanded Abstracts， 3861-3865.

Bansal R， Imhof M G， 2005， Diffraction enhancement in prestack seismic data[J]. Geophysics， 70（3）：73-79.

Berkovitch A， Belfer I， Hassin Y， et al.， 2009. Diffraction imaging by multifocusing[J]. Geophysics， 74（6）：75-81.

Khaidukov V， Landa E， Moser T， 2004， Diffraction imaging by focusing-defocusing： An outlook on seismic superresolution[J]. Geophysics， 69（6）：1478-1490.

Landa E， Shtivelman V， Gelchinsky B， 1987. A method for detection of diffracted waves on common-offset sections[J]. Geophysical Prospecting， 35（4）：359-373.

Moser T， Howard B C， 2008. Diffraction imaging in depth[J]. Geophysical Prospecting， 56（5）：627-641.

Nowak E J， 2004. Diffractor localization via weighted Radon transforms[J]. SEG Technical Program Expanded Abstracts， 23（1）：2586.