基于TP+FPT的L2-STC-Multi-h CPM遙測系統(tǒng)的高可靠性檢測算法
王西奪,賴鵬輝,李泰立,王方剛,王 巖,張 煒
(1.中國電子科技集材公司 航天信息應(yīng)用技術(shù)重點實驗室,河北 石家莊 050081;2.國防科技大學(xué) 電子科學(xué)學(xué)院,湖南 長沙 410073;3.北京交通大學(xué) 軌道交通控制與安全國家重點實驗室,北京 100044;4.北京宇航系統(tǒng)工程研究所,北京 100084)
0 引言
連續(xù)相位調(diào)制(Continuous Phase Modulation,CPM)信號具有恒包絡(luò)特性、高功率效率和低截獲率等優(yōu)點,被廣泛應(yīng)用于航空遙測、深空通信等領(lǐng)域[1-2]。在遙測系統(tǒng)中,為解決飛行器通信鏈路被阻擋,傳輸信號無法被接收天線接收的問題,通常同時使用2根發(fā)射天線發(fā)射相同的信號。但是當2根天線的信號同時對地面可見時,2路信號會相互干涉產(chǎn)生自干擾問題,這一現(xiàn)象被稱為“雙天線”問題[3]。在調(diào)制的過程中進行空時編碼是解決雙天線問題的有效途徑之一。CPM信號作為典型的遙測信號,將其與空時碼相結(jié)合,不僅能夠獲取較為客觀的分集增益和編碼增益,還能在近地場景克服信道衰落[4-5]。為了實現(xiàn)空時碼與CPM結(jié)合的高效益,文獻[6]實現(xiàn)正交空時碼與全響應(yīng)/部分響應(yīng)CPM的聯(lián)合設(shè)計,但是當通信系統(tǒng)的發(fā)射天線數(shù)大于2時,由于線性編碼不滿足逐點正交從而無法實現(xiàn)全速率傳輸,因此文獻[7]提出了一種基于L2正交的空時碼,并將其推廣到了任意發(fā)射天線數(shù)的通信系統(tǒng)中,在保有正交性的同時,碼速率不會降低。
本文在文獻[8]的基礎(chǔ)上,針對Multi-h CPM與L2正交空時碼相結(jié)合的通信系統(tǒng)采用最大似然法解調(diào)復(fù)雜度較高的問題,采用傾斜相位和脈沖截斷的算法做簡化處理,大大降低了解調(diào)的復(fù)雜度。內(nèi)容主要包括:介紹了CPM聯(lián)合L2正交空時碼的通信系統(tǒng)模型,根據(jù)2路信號波形的正交性,對最大似然解調(diào)算法進行簡化設(shè)計,并利用常見的波形擬合算法進一步減少逐碼塊判決時Viterbi算法所需要計算的網(wǎng)格狀態(tài)數(shù),實現(xiàn)了誤碼性能與檢測復(fù)雜度的折衷。
1 L2 STC-CPM通信系統(tǒng)模型
1.1 L2 STC-CPM聯(lián)合設(shè)計
L2空時碼的設(shè)計不同于傳統(tǒng)的正交空時分組碼,考慮的不再是構(gòu)造正交的碼字矩陣D,即滿足條件:DDH=I,而是構(gòu)造一種使多路信號的波形滿足相互正交關(guān)系的空時碼。令m=1,…,Lt為天線數(shù),lF=1,…,LF為一個數(shù)據(jù)流中碼塊的數(shù)目,令k=1,…,LB為一個碼塊內(nèi)時隙的個數(shù),若在一個碼塊間隔內(nèi),即當(lF-1)LBT (1) 則稱其滿足L2正交的條件,不難看出式(11)的意義與L2范數(shù)的原理一致: 相比于逐點正交,L2正交對于編碼的限制要小,并且逐點正交可以看作是L2正交的一種特殊情況。為了滿足波形正交的條件,定義相位修正函數(shù)cm,k(t),并令關(guān)于天線獨立的信息序列為dm=[dm,1,…,dm,Lf],則當前時刻CPM信號的相位表達式為: (2) 圖1 L2 STC-CPM通信系統(tǒng)Fig.1 L2 STC-CPM communication system 將L2正交的限制條件分為2個部分:自相關(guān)系數(shù)必須為1,不同天線的互相關(guān)系數(shù)必須為0。由于自相關(guān)的限制條件是與信號能量相關(guān),若2個天線傳輸?shù)哪芰肯嗤纯蓾M足,對于互相關(guān)系數(shù)的條件則滿足: cm′,k(t)]}dt=0。 (3) 由于對于?m,m′=1,…,Lt且m≠m′式(3)均要成立,即相當于共有Lt2-Lt個子條件,對一個碼塊時間進行分析,假設(shè): cm,k(t)=cm,k′(t), (4) dm,k=dm′,k。 (5) 即各天線的相位修正函數(shù)在碼塊間滿足重復(fù)編碼的條件,信息序列則滿足平行編碼的條件。因此,可將互相關(guān)條件中關(guān)于信息序列的部分項去掉,即可以化簡為: (6) 式(6)成立的條件可以分為2個,滿足其一即可: (7) (8) 不失一般性,本文考慮的是第2個等式,將式(2)帶入式(8)中可得: (9) 式中,Δck,m,m′為: Δck,m,m′=[cm,k(T)-cm,k(0)]-[cm′,k(T)-cm′,k(0)]。 (10) 可以看出,L2正交并不受每個碼塊的初始相位θm,k影響,根據(jù)假設(shè):Δck,m,m′=Δck′,m,m′,將其簡化表示為Δcm,m′,則式(9)可化簡為: (11) 因此,各天線的修正相位之差只需滿足如下形式即可實現(xiàn)L2正交: (12) 式中,i為任意非0整數(shù)。可以看出,基于L2正交的編碼設(shè)計易于推廣到任意發(fā)射天線的場景,實現(xiàn)較為簡便。令cm,r(0)=0,式(12)可以簡化為: (13) 式中,cm,r(t)的函數(shù)表達式為: (14) (15) 則各發(fā)射天線所傳輸?shù)男盘柋磉_式可以表示為: (16) 式中,s(t,d)為傳統(tǒng)的CPM信號,故式(15)可作為一種線性的修正函數(shù)。對長度為Lg的相位響應(yīng)函數(shù)進行合理加權(quán),可得到另一種修正函數(shù)為: (17) CPM信號的相位表達式為: (18) 結(jié)合式(2)和式(17),并帶入式(18),可得: (19) 觀察式(18)和式(19)可知,相對于傳統(tǒng)的CPM信號,加上相位修正函數(shù)后的CPM信號的符號集可寫成: (20) 若采用式(17)這種相位修正函數(shù)來實現(xiàn)L2正交只需要在進行CPM調(diào)制時改變第m個發(fā)射天線的符號集,進行相應(yīng)的符號映射即可。實現(xiàn)L2正交的過程中信息序列與空時碼塊的對應(yīng)關(guān)系如圖2所示(以Lt=3,LB=3為例),圖2中顯示每3個信息比特可映射為一個大小為3×3的碼塊組,由于采用平行編碼,即滿足dk=d1,k=d2,k=d3,k。 圖2 信息符號與空時碼塊對應(yīng)關(guān)系示意Fig.2 Schematic diagram of the correspondence between information symbols and space-time code blocks 對于CPM這類記憶性信號,通常采用Viterbi譯碼算法來實現(xiàn)最大似然序列檢測[9],但關(guān)聯(lián)長度較長且相位狀態(tài)數(shù)較多的Multi-h CPM信號檢測復(fù)雜度較高,在工程中實現(xiàn)高速傳輸非常困難[10-11],經(jīng)常使用簡化算法—傾斜相位與脈沖截斷聯(lián)用是較為有效的算法[12]。同時,可利用L2正交分組空時碼各路信號的波形之間的正交性,來減少檢測的復(fù)雜度。 每個碼塊的最大似然度量可以表示為: (21) (22) 考慮到引入修正函數(shù)后各路信號波形的正交性: (23) 因此,式(22)中的交叉項可以去掉,可重新表示為: (24) 由于式(24)中的2|r(t,d)|2表示的是信號的能量,與碼塊信息序列無關(guān),可以忽略,令2P為相位狀態(tài)數(shù),那么每個碼塊的解碼復(fù)雜度為2LtPMLB+Lg-1。可以看出其復(fù)雜度會隨著發(fā)射天線數(shù)的增加而線性提高。同時,采用平行編碼的方法也大大降低了檢測的復(fù)雜度,其最大似然度量可表示為: (25) 對應(yīng)的在接收端,可以定義一個修改的接收信號,表示為: (26) 則最大似然度量可表示為: (27) 算法中,CPM信號的相位表達式中的符號αi可以用Ui=(αi+M-1)/2來代替,則CPM的相位可表示為: (28) 式中,W(t)是與符號不相關(guān)的項, (29) 將式(28)中第2個等式的第1項,即累計相位項取2π的模,可得: (30) Vn=[Kn-LUn-L+Vn-1]modP。 (31) 因此,累計相位取值的集合由{0,1,2,…,2P-1}變?yōu)榱藍0,1,2,…,P-1},即累計相位的狀態(tài)數(shù)減少到了原來的一半[13]。將此時所有與CPM網(wǎng)格狀態(tài)圖相關(guān)的量定義為狀態(tài)轉(zhuǎn)移的向量: σn={Vn,Un-1,Un-2,…,Un-L+1}, (32) 圖3 脈沖截斷算法原理Fig.3 Pulse truncation algorithm schematic 觀察圖中方框圈出的區(qū)域可知,對[1.5T,2.5T]時間段波形產(chǎn)生影響的符號αi從3個減少到了2個,所涉及到的比特數(shù)目減少相應(yīng)的檢測復(fù)雜度也會降低,將新的相位響應(yīng)函數(shù)q′(t)帶入式(28)可得: (33) 式中,W′(t)可表示為: (34) 同樣的,累計相位變?yōu)椋?/p> (35) 將采用TP+FPT的簡化算法的復(fù)雜度與簡化前的MLSD算法復(fù)雜度進行對比,相關(guān)參數(shù)如表1所示。 表1 TP+FPT簡化算法與MLSD算法的復(fù)雜度對比 Tab.1Comparison of complexity between TP+FPTsimplified algorithm and MLSD algorithm 算法相位狀態(tài)數(shù)網(wǎng)格狀態(tài)數(shù)MLSD2P2LtPMLB+Lg-1TP+FPTPLtPMLB+L′g-1 同樣以ARTM CPM信號為例,采用TP+FPT簡化算法后,其相位狀態(tài)數(shù)降為16。當LB=2時,兩發(fā)一收的L2STC-CPM遙測系統(tǒng)中,Viterbi檢測時的網(wǎng)格狀態(tài)數(shù)降為2 048個,相比于具有16 384個網(wǎng)格狀態(tài)的MLSD算法,大大降低了檢測復(fù)雜度。 在兩發(fā)一收的L2STC-CPM遙測系統(tǒng)中,發(fā)射器與接收天線間的距離通常遠大于2根發(fā)射天線間的距離,因此可假設(shè)2個子信道信道響應(yīng)g0和g1的幅值a0=a1=1,當2根發(fā)射天線對接收天線均可見時,其信道響應(yīng)的相角差θ會影響信號檢測的性能,令g0,g1分別表示為g0=1,g1=exp(iθ)。 仿真采用的CPM調(diào)制方式為單指數(shù)CPM中的SOQPSK-TG,本文假設(shè)2路信號沒有時延且2個發(fā)射天線的功率相等,相干解調(diào)部分都假設(shè)對信道參數(shù)有完美的估計。令當前信噪比為5 dB,θ=0.1π,采樣點數(shù)為16,信道為高斯白噪聲信道,圖4為使用本文設(shè)計空時編碼與不使用空時編碼的參考系統(tǒng)的誤碼率仿真曲線。 圖4 L2STC-CPM遙測系統(tǒng)與CPM遙測系統(tǒng)的誤比特率隨信道響應(yīng)的相位差變化關(guān)系Fig.4 Variation of the bit error rate of the L2STC-CPM telemetry system and the CPM telemetry system with the phase difference of the channel response 可知隨信道響應(yīng)的相位差的增大,無空時編碼的系統(tǒng)誤碼性能迅速衰減,而采用L2空時碼的遙測系統(tǒng)的誤碼性能基本不受影響。因此設(shè)計的L2STC-CPM遙測系統(tǒng)可有效地解決“雙天線問題”。 圖5為在AWGN信道下,采用TP+FPT的(Multi-h CPM為ARTM CPM信號)遙測系統(tǒng)和未采用簡化算法的L2STC-Multi-h CPM遙測系統(tǒng)的誤碼曲線。由圖5可以看出,在低信噪比情況下,采用TP+FPT簡化算法對誤碼性能影響較小。 圖5 L2STC-Multi-h CPM遙測系統(tǒng)基于TP+FPT的最大似然檢測與不采用簡化算法的誤比特率隨信噪比變化關(guān)系Fig.5 Variation of the bit error rate of the maximum likelihood detection algorithm based on TP+FPT and the method without simplification algorithm of the L2STC-Multi-h CPM telemetry system with the signal-to-noise ratio 為了解決多天線遙測系統(tǒng)中2路發(fā)射信號同時對接收端可見時相互干涉而產(chǎn)生的“雙天線問題”,提出了一種基于正交設(shè)計的L2STC-CPM遙測系統(tǒng)模型。在L2STC-CPM遙測系統(tǒng)模型中,引入相位修正函數(shù)使得各路信號的波形相互正交,并且針對L2STC-Multi-h CPM遙測系統(tǒng)的解調(diào)復(fù)雜度過高的問題,提出采用TP+FPT的簡化檢測算法,大大降低了聯(lián)合檢測的復(fù)雜度。仿真結(jié)果證明,該檢測算法的誤碼性能損失較小,即遙測系統(tǒng)具有高可靠性。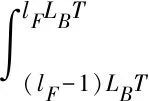






1.2 基于TP+FPT的最大似然檢測算法
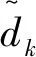




2 仿真結(jié)果分析


3 結(jié)束語

