一種基于全局最優(yōu)的改進(jìn)的正弦余弦算法

趙鵬軍， 陳克文， 黨 楠

（1.商洛學(xué)院數(shù)學(xué)與計(jì)算機(jī)應(yīng)用學(xué)院，陜西商洛 726000；2.商洛學(xué)院電子信息與電氣工程學(xué)院，陜西商洛 726000）

基于對正弦、余弦函數(shù)的研究，澳大利亞學(xué)者M(jìn)irjalili［1］于2016年提出了一種新的智能優(yōu)化算法——正弦余弦算法（Sine Cosine Algorithm，SCA），該算法通過初始化多個(gè)隨機(jī)解，利用正弦函數(shù)值和余弦函數(shù)值的變化來求解優(yōu)化問題，能夠有效避免局部最優(yōu)，是智能計(jì)算領(lǐng)域中的一個(gè)新的研究方向. 該算法具有模型簡單、可調(diào)參數(shù)少、收斂速度快、全局尋優(yōu)能力強(qiáng)等特點(diǎn)，已初步成功應(yīng)用于電力系統(tǒng)［2］、工程設(shè)計(jì)［3］、模式識別［4］等方面［5-15］. 和其他智能優(yōu)化算法一樣，SCA同樣存在易陷入局部最優(yōu)、后期收斂速度較慢等現(xiàn)象. 為提高算法的性能，本文借鑒有關(guān)算法［16-17］中的部分思想，提出了改進(jìn)的SCA（記為GSCA），利用文獻(xiàn)［16］中算法分群的思想，將種群體分成兩個(gè)子群進(jìn)行迭代操作，其中一個(gè)子群借鑒文獻(xiàn)［17］中算法第二階段的迭代方法，另一個(gè)子群中進(jìn)一步結(jié)合最優(yōu)信息，對原迭代公式進(jìn)行修改，使得在迭代過程中各個(gè)部分采用不同的迭代機(jī)制，可以提高種群的多樣性，通過種群間個(gè)體之間的合作與競爭產(chǎn)生群體智能指導(dǎo)優(yōu)化搜索，可有效增強(qiáng)算法的開采能力，避免算法陷入局部最優(yōu)，數(shù)值結(jié)果驗(yàn)證了改進(jìn)算法的可行性和有效性.

1 正弦余弦算法

在正弦余弦算法中，首先隨機(jī)初始化個(gè)體，然后以一定的概率分別利用正弦函數(shù)或余弦函數(shù)的值進(jìn)行迭代，更新個(gè)體位置，其迭代公式為

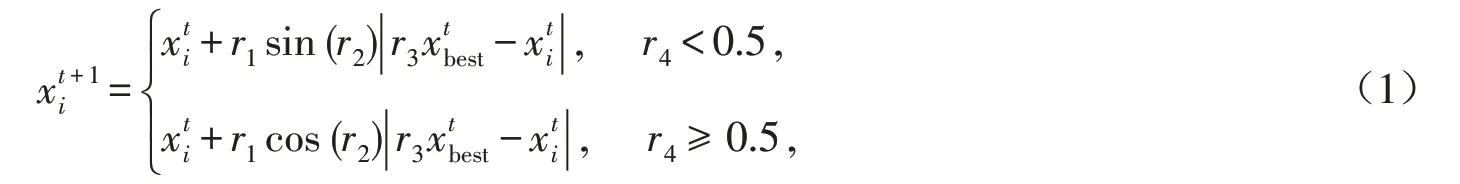
算法……