帶輸入飽和的耦合波方程的邊界反饋鎮定

武潔瓊， 任 倩

（山西大學數學科學學院，太原 030006）

本文用(?)′和(?)?分別表示對x和t求導. 考慮通過位移耦合的波振動系統：

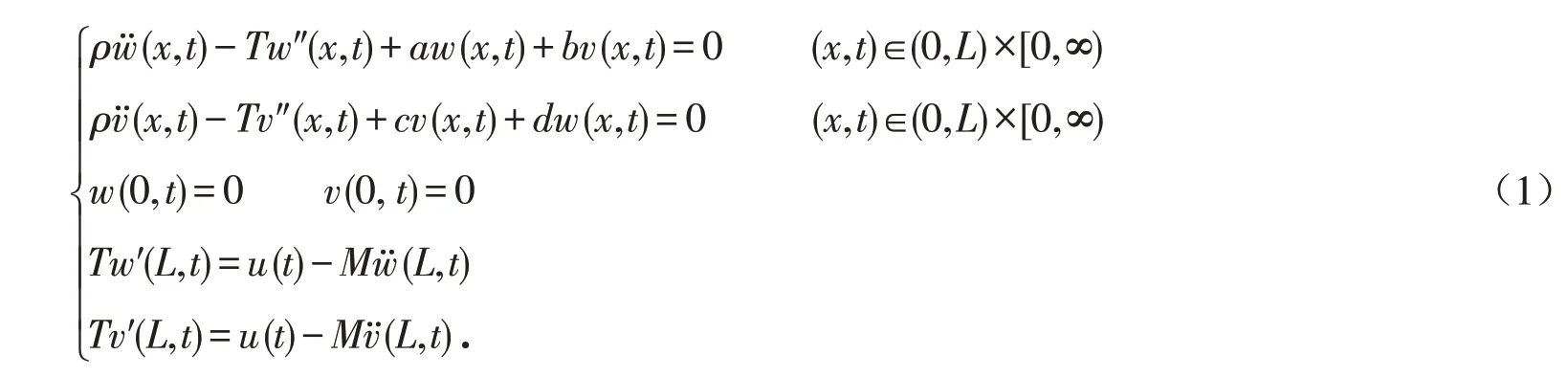
其中：L 是弦的長度；M 是尖端載荷質量；ρ 是弦的單位長度質量；T 是弦的張力；u 是控制函數. 方便起見，假設耦合系數a b c d 是正常數. 本文旨在設計具有飽和約束［1］的反饋控制u 以使得耦合波系統的閉環系統指數穩定，即設計反饋控制u(t)滿足

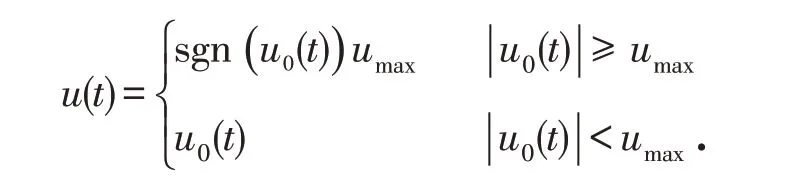
其中：sgn(?)是符號函數；u0(?)是要設計的控制函數；umax是飽和限度. 為了消除輸入飽和約束效應，引入一個輔助系統. 通過構造一個適當的積分Lyapunov 函數，證明受控的閉環系統是指數穩定的. 最后，借助Galerkin方法證明了閉環系統的適定性.

控制約束是現代工程學的一個普遍要求. 自控制約束產生以來，帶約束的控制問題就受到了許多學者廣泛的關注. 讀者可以參考文獻［1-5］進一步了解控制約束的相關內容.

關于波方程的鎮定問題已有許多學者研究. 文獻［6］設計了一種基于觀測器的邊界控制方法以實現一般邊界諧波擾動下的波的漸近穩定. 文獻［7］針對不穩定波設計了一種邊界控制器，實現了閉環系統的指數穩定. 文獻［8］中采用了backstepping法設計了一個邊界控制，證明了閉環系統的指數穩定性. 文獻［9］研究了不穩定波的邊界輸出反饋鎮定問題，設計了輸出反饋控制器使得閉環系統指數穩定. 文獻［6-9］的控制函數沒有任何約束條件. 文獻［4］研究單個波系統的反饋鎮定性，假設控制函數滿足上面的約束條件，設計了相應的邊界輸出反饋……