復雜邊界田塊旋翼無人機自主作業路徑規劃

黃小毛 張 壘 TANG Lie 唐 燦 李小霞 賀小偉

(1.華中農業大學工學院，武漢 430070；2.愛荷華州立大學農業與生物系統工程系，埃姆斯 IA 50011；3.華中農業大學信息學院，武漢 430070；4.塔里木大學現代農業工程重點實驗室，阿拉爾 843300)

0 引言

與地面機器相比，無人機空中作業具有通過性強、效率高、精度高等優點，特別適合于植保、遙感、巡查和播撒等作業環節。作業路徑是無人機自主作業時機器軌跡控制的跟蹤目標，在很大程度上決定機器作業過程的作業質量、效率和總消耗。因此無人機作業路徑的規劃和優化工作具有重要意義。

在目前農機領域作業路徑的相關研究中，針對地面作業機器的居多[1-18]，針對農用無人機作業路徑的研究不多。MOON等[12]針對噴粉無人直升機，提出基于田塊分區處理操作的路徑規劃方法。BARRIENTOS等[13]將待作業區域進行網格化處理，提出一種基于任務協商機制的多架無人機協作圖像采集作業路徑規劃算法。VALENTE等[14]在此基礎上提出一種基于“和諧搜索”(Harmony search,HS)的啟發式搜索算法，求解遍歷網格的最優次序。國內相關的研究目前還處于起步階段，徐博等[15-16]對五邊形邊界單田塊的無人機作業路徑提出了具體的算法，并對多田塊路徑調度優化進行了研究。徐東甫等[17]、劉浩蓬等[18]分別將簡單四邊形邊界的規劃路徑應用到無人機赤眼蜂投放和噴霧試驗中。王宇等[19]提出一種基于柵格模型的路徑規劃算法。彭孝東等[20]針對固定翼無人機作業過程中轉彎方式進行了詳細的討論。以上研究的共同特點是作業田塊的邊界較為簡單，均可簡化為凸多邊形，而非實際應用中遇到的復雜邊界田塊。

本文針對旋翼農用無人機作業時可能遇到的各種復雜田塊邊界形狀的問題，提出一種對田塊邊界形狀具有普適意義的旋翼無人機作業路徑規劃算法，以獲得凸多邊形、凹多邊形、帶孔洞多邊形或多個多邊形的復雜邊界田塊下的飛行作業軌跡。

1 作業路徑規劃的基本原理

1.1 旋翼無人機特點及路徑規劃的基本要求

與大田地面作業機器及固定翼飛機相比，旋翼農用無人機具有不與地面接觸、可懸停、可任意方向移動等特點，因此其作業路徑規劃應滿足以下基本要求：有效工作路徑(即作業航線)做到對待作業田塊所有區域的全覆蓋，重復作業及遺漏作業面積盡可能小；航線間跳轉轉移等非工作路徑總長度盡可能小；無需考慮轉彎及碾壓問題；算法的時間消耗不能太長；具體作業類型及應用場合的其他要求(如避障)。

1.2 數據定義及算法流程

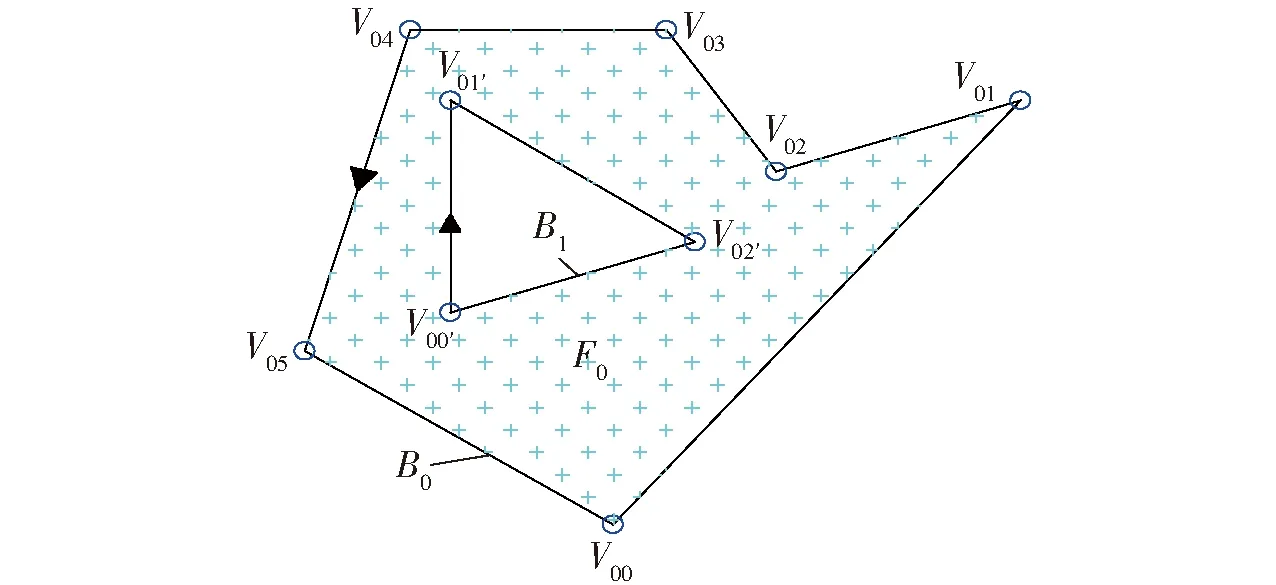
圖1 田塊邊界及頂點存儲順序示意圖

本文只針對常見的二維田塊，用一組多邊形分別代表田塊的外邊界和內邊界，且外邊界以逆時針方向、內邊界以順時針方向依次存儲各頂點(如圖1所示)。通過分析可知采用多邊形表征田塊區域時具有以下特點：每個田塊有且只有一個外邊界，而可能沒有也可能有多個相離的內邊界，且內邊界一定包含在外邊界內部；每個邊界都是一個簡單多邊形(除相鄰邊外，其他各邊之間互不相交)，可以是凸多邊形也可以是凹多邊形；每2個田塊之間的邊界均為相離關系(既不相交也不相互包含)。這些特點既是后續算法中導入的田塊邊界的合理性規定，也是計算機能夠對多邊形邊界進行分組進而自動識別田塊的依據[21]。

以多邊形邊界和作業基本參數為輸入條件，以獲得旋翼無人機飛行作業路徑為目標，本文設計的算法基本流程如圖2所示。

圖2 算法流程圖

1.3 邊界合規性檢查及分組

田塊邊界一般通過人工手持GPS直接打點或在GIS系統中鼠標打點獲得，打點、存儲的順序可能具有隨意性，不一定完全符合1.2節中的規定。因此經緯度球面坐標轉換成直角坐標后，首先需要對表征邊界的多邊形進行合規性檢查，對不合要求的地方進行調整，以保證后續處理順利進行。然后，通過分組算法[21]確定多邊形之間的關系，即從數據結構上建立田塊的概念。如從圖3a中輸入的B0、B1、B23個邊界多邊形，通過分析它們之間的包含關系，分組后分別建立F0(圖1)和F1(圖3b)2個獨立的田塊區域。

圖3 邊界合規性檢查及分組

1.4 填充線求解

多邊形填充是計算機圖形學中的經典問題[22]，在計算機動畫、數控型腔銑削、3D打印和機器人等領域均有應用[21]。利用掃描線及多邊形邊線的連貫性原理，采用有序邊表法進行快速求交解算，可避免傳統做法中對每一組線段進行逐一相交性測試，從而大大提高了求解效率和速度。

對于給定的任意形狀的單一多邊形，用一組水平或垂直的掃描線進行掃描，對于每一掃描線而言均可求出與多邊形邊的交點，且交點成對出現，位于多邊形內部的交點線段即為填充線。對于孔洞多邊形而言，分別求取外邊界多邊形B0、內邊界多邊形B1～Bn的填充線，得到填充線段集合{L0}～{Ln}，再通過減法布爾運算，即可得到孔洞多邊形區域的填充線集合，即航線集合{Pi}。對于孔洞多邊形田塊Fi而言，航向角θ條件下的作業航線Pi(θ)計算式為

(1)

以田塊F0為例，外邊界多邊形B0與內邊界多邊形B1的填充線分別如圖4b淺藍色線條和圖4c紅色虛線條所示，二者作減法布爾運算后的結果即為田塊F0在航向角為0條件下的作業航線，如圖4a淺藍色線條所示。

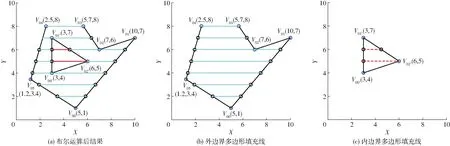
圖4 孔洞多邊形填充線的求解過程

1.5 活性邊表法

單個多邊形的填充線求解時，掃描線與多邊形邊的交點具有一定規律性，因此求解時不需要將每一條掃描線與每一條邊進行求交測試并逐一解算交點，而是運用活性邊表法快速求解。實施過程中用邊表(Edge table，ET)來確定哪些邊是下一條掃描線求交計算時應及時加入運算的邊，將與當前掃描線相交的邊稱為活化邊(Active edge list，AEL)，其個數可能不唯一且可動態變化。由活化邊組成的表稱為活性邊表(Active edge table，AET)，基于活性邊表的多邊形填充線求解算法稱之為活性邊表法或有序邊表法。

作為存儲多邊形各邊的一種數據結構，邊表用來表示對于某條掃描線而言第1次出現的邊的信息。以水平掃描線(即航向角為0)為例，每個節點的信息為(Ymax，dX，XYmin，next)，其中Ymax為對應邊的最大Y值，dX為沿該邊從當前掃描線到下一條掃描線之間的X方向增量(當掃描線間距為1時為該邊斜率的倒數)，XYmin為該邊的下端點的X坐標，next為指向下一條邊的指針。建立邊表時，先按下端點的縱坐標(Y值)對所有邊作分類和排序，再將同一組中的邊按下端點X坐標遞增的順序進行排序，X坐標還相同的按dX遞增的順序進行排序。圖4b中多邊形的邊表如表1第2列所示(表中“→”表示指針next)。

表1 活性邊表法實施過程示例

對應的，活性邊表AET中每個節點的信息也由4部分組成，即(Ymax，dX，XYmin，next)，其中Ymax、dX、next指針的含義同邊表。當作業幅寬w不等于1時，dX=ΔX/w，式中ΔX為對應邊在兩掃描線間的X方向增量。與邊表ET節點信息的主要差別在于第3個信息，XYmin為邊與當前掃描線交點的X坐標而不是當前邊的下端點X坐標。活性邊表的生成是基于邊表的，而由活性邊表生成成對的交點即為填充線段的端點。圖4b中多邊形的活性邊表及交點如表1第3、4列所示。

活性邊表法求解多邊形填充線段的流程如圖5所示。對于每一條掃描線而言，對應的處理步驟如下[23]：

(1)對于掃描線Y=y，若對應的ET中非空，則將其所有的邊從ET中取出并且插入到邊的活性邊表AET中，并對AET中各邊按XYmin及dX或ΔX遞增排序。

(2)若相對于當前掃描線的AET非空，則將AET中的邊兩兩依次配對，即第1、2邊為一對，第3、4邊為一對，依此類推，每一對邊與當前掃描線的交點所構成的區段位于多邊形內，即為對應的填充線。

(3)將當前掃描線的縱坐標Y累加w，即Y=Y+w。

(4)將AET中滿足Y=Ymax的邊刪去。

(5)將AET中剩下的每一條邊的X域累加dXw，即X=X+dXw。

(6)重復執行步驟(1)，直至AET中邊全部刪除。

圖5 活性邊表法求解多邊形填充線段算法流程圖

1.6 航線排序優化

上文中每一填充線即為飛行器作業時的具體航線，由于填充線段的長度、位置各不相同，因此航線間存儲順序將決定遍歷時航線跳轉距離和遍歷過程的總軌跡長度。若將每一條航線視為一個城市，這將是一個典型的旅行商問題(TSP)，屬于NP-hard。本文主要采取文獻[5]中的貪婪算法進行求解，該算法屬于組合優化問題的常規求解算法，雖然所得結果不一定為最優，但算法穩定可靠，具有實用性。具體實現過程見相關文獻，此處不再贅述。

航線間轉移時，轉移路線與田塊邊界之間存在兩種情況：一種是包含關系，即轉移線段全部包含在某一田塊的內部(包括邊界上)，也就是無人機轉移過程中始終處于邊界內部；另一種是非包含關系，即轉移線段上，除端點外，還有第3點處于邊界外部，也就是說無人機轉移過程中會跳到田塊邊界的外部。因田塊邊界外部可能存在高于作業高度的障礙物(尤其在田塊間轉移時)，為確保安全，有必要找出第2種情形下的線段并進行必要處理。

采用“安全邊界相交性測試法”來判別某條候選轉移路徑線段Ji與田塊邊界多邊形組{Bi}是否屬于非包含關系。具體做法如下：根據障礙物情況，人為設立安全距離參數d和安全高度參數h；將田塊邊界多邊形組{Bi}向外偏置d(外邊界擴大、內邊界縮小)，得到偏置后多邊形組{B′i}；判斷轉移線段Ji與多邊形組{B′i}的相交性，若相交，則視為“危險轉移過程”。

如圖6所示，對于田塊F0的某條候選轉移路徑Ji(對應線段KiKj)來說，因為線段KiKj與外邊界B0偏置后多邊形B′0存在交點C1和C2，故該轉移過程被視為危險轉移過程。對于此類轉移過程，實際操作時，飛機先從Ki點從作業高度h0拉升至安全高度h，轉移至Kj點后再下降至作業高度繼續作業。計算轉移路線長度時在原計算值上加上2(h-h0)。上述過程中涉及到多邊形偏置算法、多邊形與線段間求交算法，也是計算機圖形學中經典問題[21]，限于篇幅問題，不再贅述。

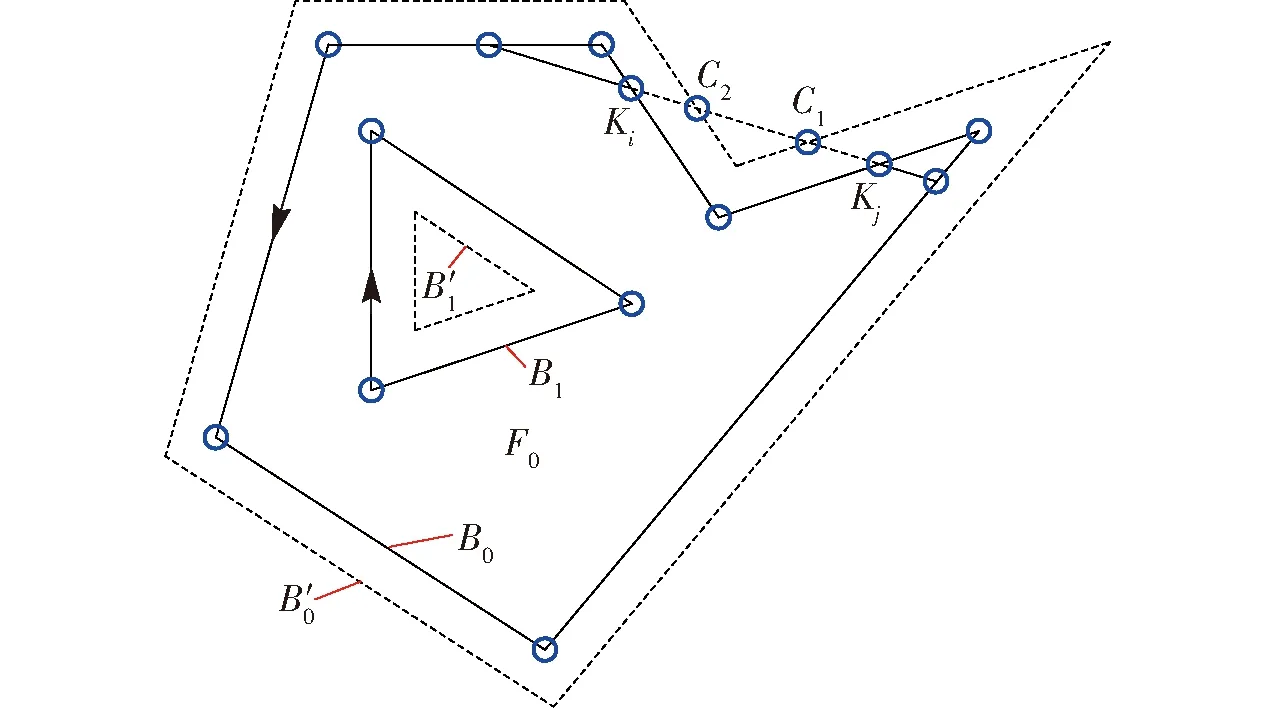
圖6 安全邊界相交性測試

1.7 航向優化

作業飛行的總線路長度和時間，除了與航線間調度次序有關，還與航線的方向有關。這里采用最小跨度法和步進旋轉法進行綜合優化，前者可精確確定單一凸多邊形邊界田塊的最佳航向，后者則用于近似確定其他類型(凹多邊形及孔洞多邊形)田塊的最佳航向。

區域跨度是指某一平面區域Q能夠剛好被某一對方向為θ的平行線夾住時平行線間的間距D。此時，平行線稱之為支撐平行線，θ稱之為跨度方向角，D稱之為區域Q在θ方向上的跨度。分析可知，凸多邊形在任意方向上都有一對支撐平行線，且跨度值隨方向角變化而變化，按照最小跨度對應方向布置填充線時數量最少，因此航線間轉移距離將最短[24]。對于凸多邊形而言，其跨度有3種形式，分別是點對式、點邊式和邊對式(圖7)。文獻[24]已證明凸多邊形區域的最小跨度方向一定出現在點邊式中。因此找出最小跨度方向角即為凸多邊形田塊的最優航向角。

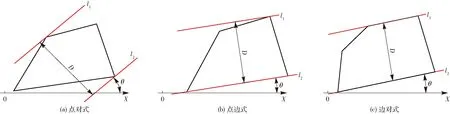
圖7 凸多邊形跨度的3種形式

對非單一凸多邊形田塊而言，可采用“步進旋轉法”進行近似求解。其本質上是一種窮舉法，計算時，從0開始、以dθ為步距，計算所有可能航向下的航線，比較線路總長度，取最小值對應的航向θ為最優航向。

當θ≠0時，通過兩次坐標變換可簡化計算過程。先將多邊形頂點繞其軸對齊包圍盒(Axis-aligned bounding box，AABB)中心點(xr0,yr0)順時針旋轉θ(正變換)得到旋轉后多邊形頂點，基于活性邊表法計算得到中間航線，再將航線端點(x0,y0)繞包圍盒中心逆時針旋轉θ(逆變換)即得到所需的真實航線的端點(x,y)。逆變換時計算公式為

(2)

而順時針變換時，只需將θ值取相反數即可。

2 實例仿真計算

前述全部算法過程在Visual C++ 6.0平臺上編碼實現，在Intel Corei7-3370 CPU、3.4 GHz主頻、8 GB內存、Windows 7操作系統環境下，分別對4組典型復雜性的人工假想邊界和實際邊界在多組不同工作參數條件下進行兩次試驗，以測試算法穩定性和計算效率。

實際田塊1的邊界利用Google Earth獲取并以KML文件格式導出，實際田塊2邊界通過無人機開源軟件Mission Planner獲取并以其自定義的POLY格式導出，二者都經過坐標轉換，將地球經緯度坐標轉換成平面直角坐標后再進行計算測試[6]；假想田塊邊界利用CAD繪制并以DXF格式導入。計算過程中，算法對導入的邊界自動進行合規性檢查并進行分組；對于單一邊界且為凸多邊形的田塊采用最小跨度法優化航向，其他的情形則采用“步進旋轉法”(步距取0.5°)優化航向；采用貪婪算法進行航線排序優化，計算航線間轉移距離時，若不考慮障礙物則直接計算直線距離，如考慮障礙物影響，則對每一潛在轉移軌跡與安全邊界進行安全檢查，對不安全轉移過程作高度方向上補償，轉移距離加上兩倍高度差(即安全高度與作業高度之差)。結果數據中路徑總長度通過軌跡線段長度求和得到，算法耗時通過GetTickCount()函數獲取算法運行前后的系統時間后再求差得到，且測試時包括界面顯示更新相關操作。

2.1 不考慮邊界障礙物情況下的仿真試驗

聚焦田塊邊界多邊形的復雜性，不考慮邊界上障礙物的影響或障礙物高度低于作業高度而不影響轉移過程安全，測試結果相關數據如表2所示。表中，優化率ε為S2相對于S1的降低幅度，即ε=(S1-S2)/S1×100%，式中，S1為只進行航線排序優化而不進行航向優化(人工指定與邊界上某一邊的方向一致)時非工作路徑(即航線間跳轉路徑)的長度，S2為同時進行航向及航線排序優化時非工作路徑的長度。計算示例的部分結果截圖(因篇幅限制，只取其中部分典型結果)如圖8所示。

2.2 考慮邊界障礙物情況下的仿真試驗

為進一步擴大算法的應用范圍，假設上述4個田塊邊界上存在障礙物且高度大于作業高度，在前述同時進行航向及航線排序優化試驗基礎上，繼續增加轉移過程的安全性判斷及處理算法的測試。設置作業高度為2 m，安全高度為6 m，安全距離為1 m，測試結果如表3及圖9所示。圖9較圖8增加了高度調整和安全邊界，分別采用黑色小圓圈和粉色多邊形表示。

3 討論

不考慮障礙物影響時，從表2中數據及圖8所示計算實例典型結果截圖可以看出，本文算法能夠處理各種復雜邊界形狀類型的田塊，這些田塊的邊界形狀復雜程度明顯高于現有可查的相關文獻中的算法實例，同時對于作業方向的優化是自動完成的，有別于現有商用無人機自帶處理軟件(包括Mission Planner)需要用戶人工指定設置。

對比不進行航向優化而只進行航線排序優化的規劃結果，二者同時優化時有效工作路徑(即航線)的總長度基本不變，但對非工作路徑的優化效果明顯，優化幅度從23.04%到45.98%不等。這是因為有效工作路徑要覆蓋作業區域，其總長度與工作幅寬之積近似等于區域面積，而無效工作路徑為航線間跳轉軌跡，其總長度與航向和航線間調度次序高度相關。進一步，如不進行航線排序優化，則后果更加嚴重。如圖8g所示，同樣航向情況下，不排序情況下非工作路徑長度為15 269.30 m，為表2中相同算例排序優化結果(對應圖8e)2 058.88 m的7.4倍，是有效工作路徑7 042.57 m的2.2倍。

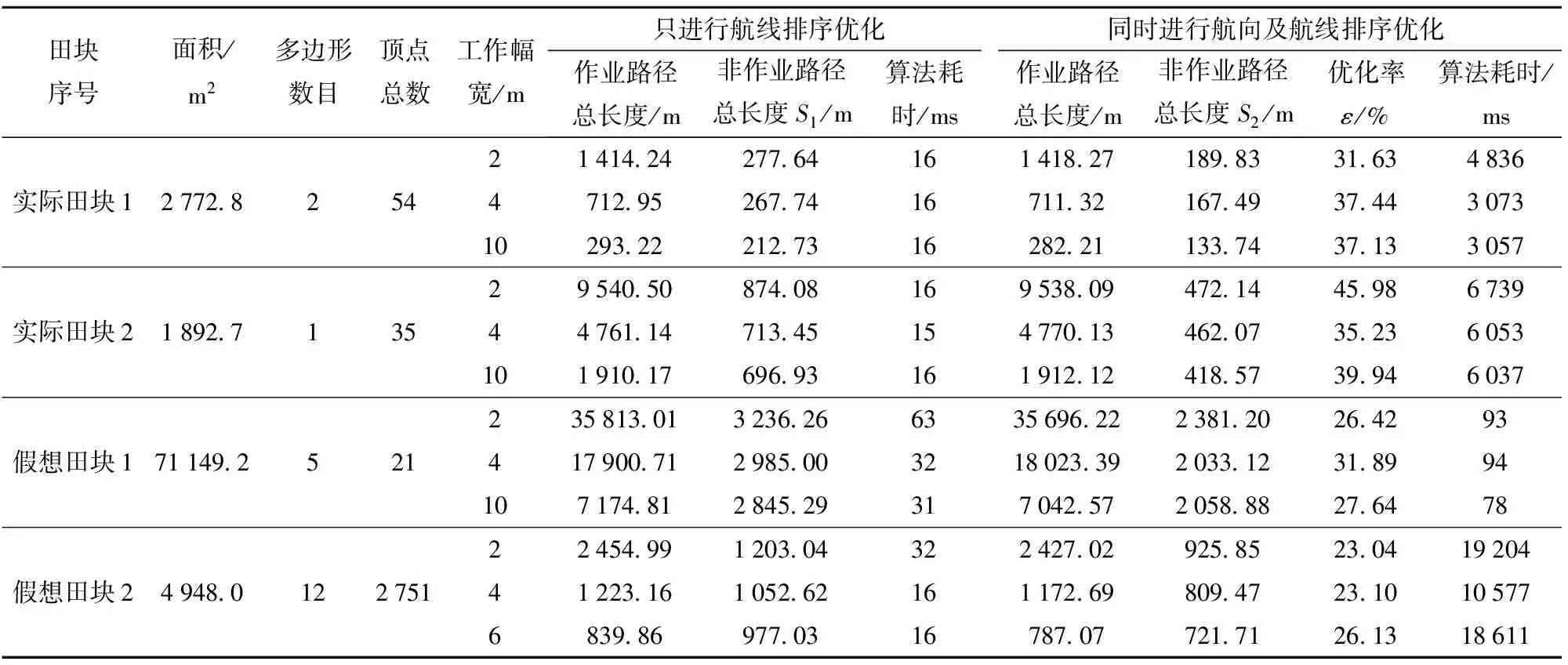
表2 不考慮障礙物影響情況下的算法測試結果

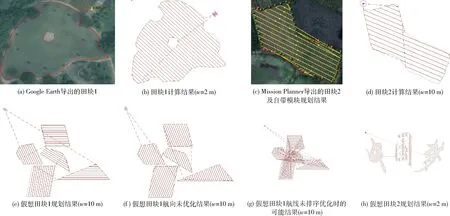
圖8 不考慮障礙物影響情況下部分計算實例結果截圖

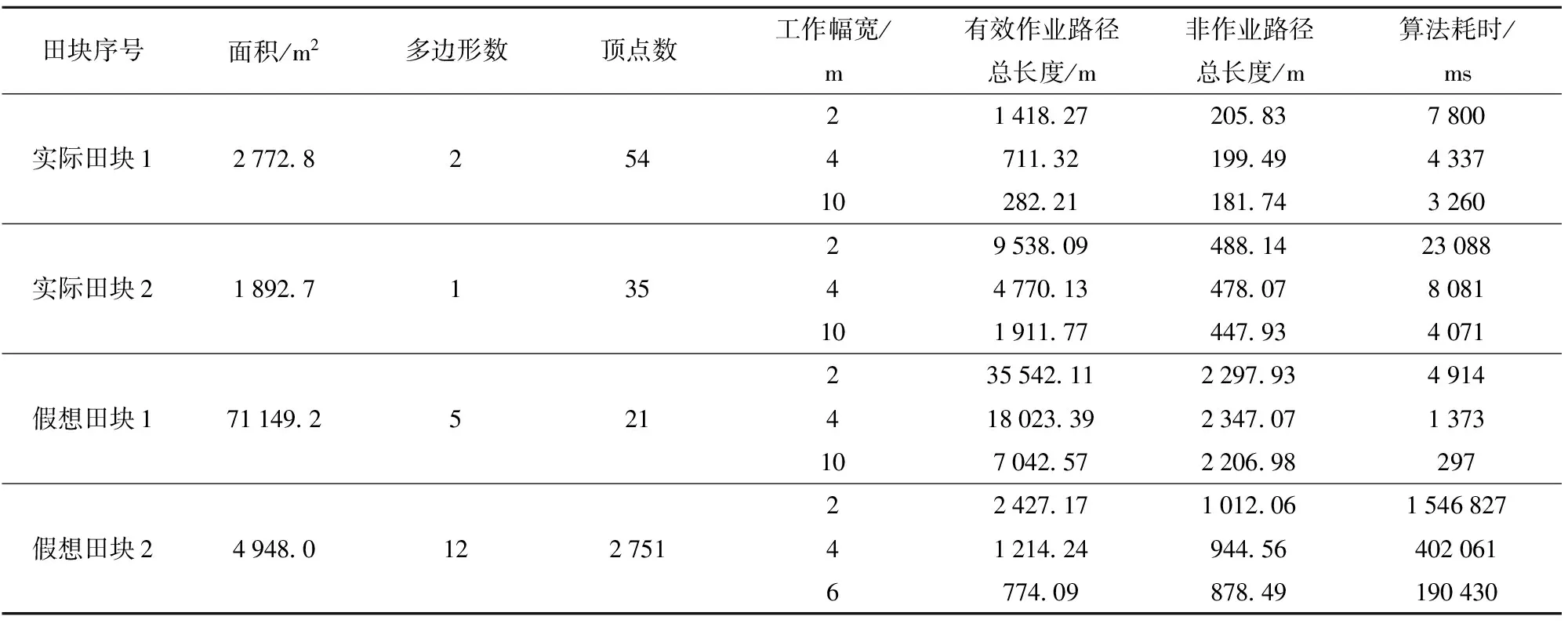
表3 考慮障礙物影響情況下的算法測試結果

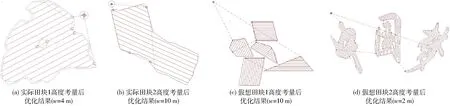
圖9 考慮障礙物影響情況下部分優化計算實例結果截圖

此外算法耗時隨著田塊數量和邊界頂點數目增加而增加，這是因為初步航線計算和航向優化都是以田塊為單元逐一進行的，田塊數量的增加必然會增加優化的工作量，而邊界頂點數目的增加則會增加邊界分組、多邊形凹凸性判斷及活性邊表法求交處理的工作量。同時算法耗時還會隨機器工作幅寬的減少和田塊面積的增加而增加，這是因為幅寬越小、田塊面積越大，航線的數量越多，需要求交的次數愈多、排序優化TSP的規模越大。對于航向的優化，基于最小跨度法的算法執行效率明顯高于步進旋轉法，但只適合于單一邊界且為凸多邊形的田塊(如假想田塊1)，通用性不如步進旋轉法。算法總耗時從15 ms到19.2 s不等，考慮到計算優化過程是作業前離線完成的，對實時性要求不高，因此本文算法的實時性特性完全能夠滿足無人機使用時對路徑規劃的及時性需求。

考慮障礙物影響時，對比表3及表2中計算結果，在同樣試驗條件下，有效工作路徑總長度幾乎沒有變化，而非有效作業路徑長度普遍增加，主要原因是某些航線間轉移路徑中增加了高度調整的補償而且航線間排序可能因此而改變。此外，算法耗時的增加幅度較大，特別是在多邊形數目和頂點數較多且航線數量也較多時(如假想田塊2在工作幅寬2 m時)，這是因為航線排序時要對每一潛在航線間轉移過程進行安全性判斷，極大增加了算法的工作量。好在算法的穩定性很好，計算效率也基本滿足離線規劃的要求。

無人機實際作業過程中，還可能遇到因為續航和載重等原因導致的消耗品按需補給、田塊間高度差和多機協同作業等問題，這是路徑規劃工作中需要進一步深入研究的內容。

4 結論

(1)提出并實現一種對于田塊邊界形狀具有普適性意義的旋翼無人機作業路徑規劃算法，可以快速獲得凸多邊形、凹多邊形、帶孔洞多邊形或多個多邊形等各種復雜邊界田塊下的飛行作業軌跡。

(2)利用假想田塊、實際田塊的多組仿真測試試驗表明，所設計的算法運行穩定可靠、效率高、優化效果明顯，可滿足農用無人機作業時對路徑規劃過程的準確性、實時性和穩定性等相關要求。在不考慮障礙物影響時算法耗時15 ms～19.2 s，相比于只進行航線排序優化的情況，同時進行航向和航線排序優化后，航線間轉移路徑總長度下降了23.04%～45.98%，而考慮障礙物影響時的處理耗時也在離線應用的可接受范圍內。