第28屆全國中學生物理競賽預賽試卷第13題的另兩種解法

侯位鋒

(浙江省諸暨中學 311800)

原題：電荷量為q的正電荷，均勻分布在由絕緣材料制成的質量為m半徑為R的均勻細圓環上，現設法加外力使圓環從靜止開始，繞通過環心的軸線勻加速轉動．試求從開始轉動到環的角速度達到某一值ω0的整個過程中外力所做的功．已知轉動帶電圓環的等效電流為I時，等效電流產生的磁場對整個以圓環為周界的圓面的磁通量為Ф=kI，k為一已知常量．不計電荷作加速運動所產生的輻射效應．

原解法

解析當環角速度達到ω0，環的動能為

(1)

若在時刻t，環轉動的角速度為ω，則環上電荷所形成的等效電流

(2)

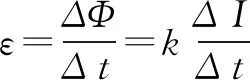
(3)

(4)

環加速轉動時要克服感應電動勢做功，功率為

P1=εI

(5)

因為是勻加速轉動，所以ω和I都隨時間t線性增加．若角速度從零開始增加到ω0經歷的時間為t0，則有

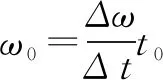
(6)

若與ω0對應的等效電流為I0，則整個過程中克服感應電動勢做的功為

(7)

(8)

外力所做總功

另解法一動力學方法

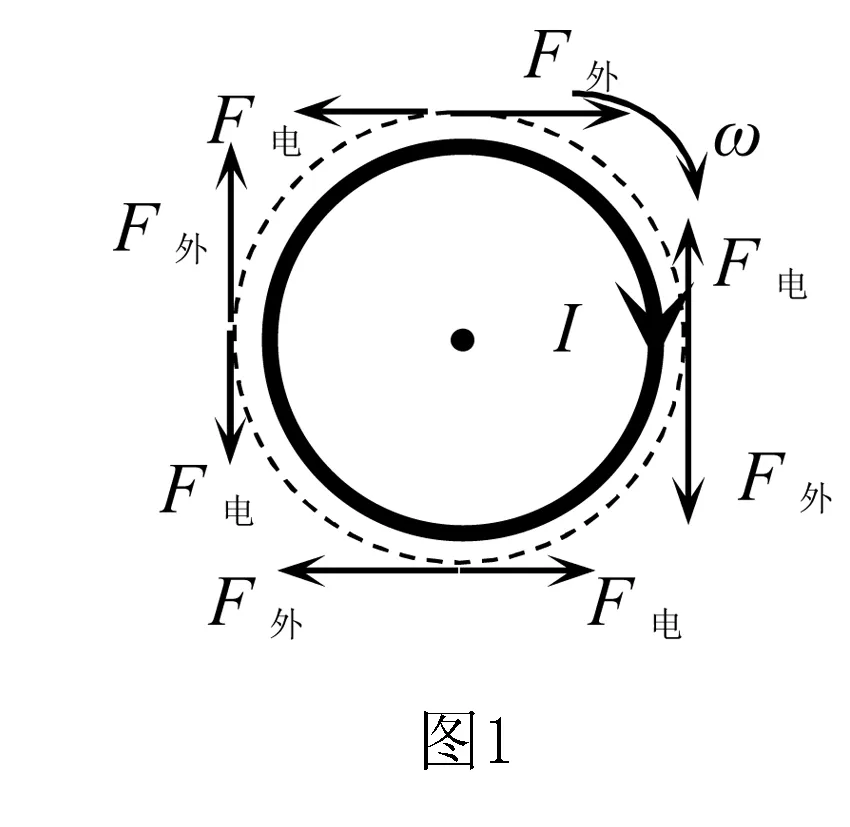
解析如圖1所示，圓環在勻加速轉動過程中，形成等效電流(變化)，產生一變化的磁場，變化的磁場產生一渦旋電場，而帶電圓環在渦旋電場中會受到電場力F電作用(沿圓環的切線方向且與圓環轉動方向相反)，要使圓環勻加速轉動，則外力F外應該沿圓環的切線方向且與圓環轉動方向相同．為求外力F外做的功則圓環勻加速轉動過程中可以等效為一質量為m的質點，在外力F外和F電作用下做勻加速運動，速度為v=ωR．

若在時刻t，環轉動的角速度為ω，則環上電荷所形成的等效電流

(1)

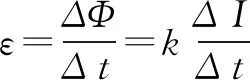
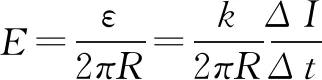
(2)

由v=ωR及……