超音速懸索火箭橇水平運動偏差仿真分析*

游培寒,趙未平,白晨陽,祝逢春

(1 北京航空工程研究中心, 北京 100076； 2 南京林業大學， 南京 210037)

0 概述

懸索火箭橇[1]是一種約束彈道試驗裝置，可用于測試空空武器的近炸引信等需要高速精確定向飛行的相關設備。如圖1所示，它利用兩根平行布設并拉緊的懸空索道作為滑軌，約束火箭橇體于兩根懸索中間，發動機推動火箭橇在懸索約束下定向運動。橇體定向飛行控制精度是懸索火箭橇系統設計的難點，文獻[2]分析了橇體飛行過程對懸索的下拉作用，文中通過有限元建模仿真方法分析了側風大小、懸索初始拉力和懸索彈性模量對飛行橇體水平偏移的影響。

圖1 懸索火箭橇

首先介紹利用Newton法對懸索進行3D運動建模；接著介紹了火箭橇橇體運動建摸和火箭橇運動有限元計算方法；然后介紹有限元建摸仿真分析得到的側風大小、懸索初始拉力和懸索彈性模量對橇體水平運動控制精度的影響；最后給出結論。

1 基于Newton法的懸索運動建模

橇體飛行的水平偏移主要因為懸索的彈性應變造成，這種彈性應變還會引起橇體在垂直方向的下拉運動，所以必須在3D空間中對懸索進行運動建模，這里用Newton法對懸索運動建摸[3],公式如下：

(1)

(2)

(3)

圖2 懸索微元的受力分析

X、Y、Z分別代表懸索單位長度在x、y、z軸3個方向的外力，當懸索微元不處于火箭橇位置時在x方向并不受力有：

ifk≠r,Xk=0

(4)

k為懸索微元序號，r為火箭橇運動位置。

y方向受力主要來自索道本身的重力有：

ifk≠r,Yk=0

(5)

Z主要來自于索道自身受到的側向力，有：

(6)

式中：cz為懸索的側向阻力系數；Az為懸索靜態單位長度對應的懸索動態側向截面積；d為懸索直徑；vz為側向風速；ρ為空氣密度。Td,k為懸軸第k個微元的動態拉力[4]有：

Td,k=T0+Eεd,kAx

(7)

其中Ax為懸索橫截面積；E為懸索的彈性模量；T0為懸索的初始拉力；εd,k為第k個微元的應變。

2 火箭橇體運動建模

前期試驗表明橇體飛行過程中姿態變化很小，可以將橇體簡化為一個運動質點，橇體軸向方向始終與懸索方向一致，橇體位置的懸索在y方向和z方向與橇體一起運動，在y方向有:

Td，kcosβd,ksinαd,k)-(mr+m?s0)g+

(P-Nmr-Γ)·cosβd,ksin(αd，k-αd,k+1)

(8)

其中：yd,r為橇體在y方向的動態坐標;yd,k為懸索微元在y方向的動態坐標;P為火箭橇發動機的推力;N為摩擦力系數；αd,k為懸索第k個微元軸向與x方向的夾角在xy平面的映射：

(9)

βd,k為第k個微元軸向與x方向的夾角在xz平面的映射：

(10)

mr為橇體質量:

(11)

式中：m0為橇體的初始質量;mP為發動機裝藥質量;TP為發動機的工作周期;Γ為橇體的軸向空氣阻力[5]:

(12)

式中:cr為橇體軸向空氣阻力系數；vr為橇體飛行速度；Ar為橇體軸向截面積。

(P-Nmr-Γ)cosαd,ksinβd,k

(13)

式中：zd,r為橇體在z方向的動態坐標；zd,k為懸索微元在z方向的動態坐標；crz為橇體側向空氣阻力系數；Arz=ldr為橇體側向截面積；l為橇體長度；dr為橇體直徑。

在x方向由于橇體在懸索上滑行，懸索只給橇體一個摩擦阻力，所以在x方向橇體運動模型為：

ifk=r

(14)

xd,r為橇體在x方向的動態坐標。而懸索微元只受到橇體的摩擦力，可以近似認為在x方向懸索微元的運動模型為：

ifk=r

(15)

xd,k為懸索微元在x方向的動態坐標。橇體運動建模中受力分析參考圖3所示。

圖3 橇體運動受力分析

3 懸索火箭橇運動有限元計算方法

第二步確定有限元計算的時間步長。時間步長應保證微元計算速度高于懸索波速vb的兩倍，即[1]：

(16)

第三步設定邊界條件。火箭橇運動過程中，索道兩端固定不動，即：

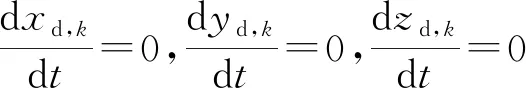
(17)

第四步設定初始條件。設定初始懸索拉力T0，設定初始側風速度vz;設置懸索微元的初始坐標有：

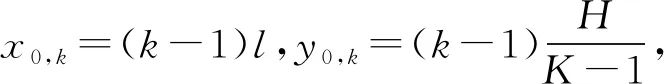
z0,k=0k=1,…,K

(18)

同時各微元的動態速度為零。

(19)

H為懸索兩端高度差。選擇懸索微元坐標為火箭橇初始位置，比如橇體初始位置在第10個微元位置則有：

r=10,x0,r=x0，10,y0,r=y0，10,z0,r=z0，10

(20)

第五步進行迭代計算。采用龍格庫塔法迭代計算懸索K個微元的位置、速度和加速度[2]。其中當k≠r時，采用式(1)～式(7)計算加速度，然后計算各點的速度和位置變化；當k=r時，采用式(8)、式(13)、式(15)計算該點的加速度，進而推導出速度和位置變化。然后利用式(8)、式(13)、式(14)計算橇體的加速度、速度和位置，用橇體位置距離最接近的懸索微元序號更新橇體位置r。如此反復直至橇體運動至懸索末端為止。

4 火箭橇水平運動控制精度分析

以國內某超音速懸索火箭橇試驗系統的相關參數為計算依據，分析側風、初始拉力和懸索彈性模量對橇體水平運動控制精度的影響。索道長度為280 m，索道起點比終點高出5 m，懸索單位長度質量m=0.039 kg/m，懸索的彈性模量E=3.4×109Pa/m，懸索的側向阻力系數cz=0.6，懸索直徑d=0.008 m。索道設計初始拉力T0=2 400 kg。

橇體采用改進的70 mm火箭彈發動機制成，其初始質量m0=10.36 kg，裝藥質量mP=3.6 kg，發動機工作周期TP=0.65 s，發動機的平均推力P=10 000 N，橇體的軸向空氣阻力系數cr參考文獻[4]查表擬合得到，橇體軸向截面積Ar=0.003 8 m2；橇體側向空氣阻力系數crz=0.65，橇體長度l=1 m，橇體直徑dr=0.07 m。橇體的初始位置r=10。

對懸索進行網格劃分，單個懸索微元長度為?s0=1 m，共劃分出281個懸索微元。龍格庫塔法迭代計算的時間步長為Δt=10-4s。

為了簡化問題,下面的仿真分析做了以下假設：一是兩根平行布設的懸索特性參數和運動狀態完全相同。二是側風方向與索道方向垂直，側風風場均勻分布,速度恒定。三是設懸索與橇體之間的摩擦恒定。

4.1 側向風大小對水平運動控制精度的影響

側風是造成火箭橇水平偏移的主要原因。在近期進行的火箭橇發射試驗中實際測得側風風速為4 m/s，火箭橇成功穿過了一個布設距離終點5 m、寬度大于橇體寬度0.01 m的縫隙，說明在這里橇體的水平運動控制精度在0.01 m以內。下面部分分析橇體水平控制精度與側風風速之間的關系。

設側風風速vz=5 m/s(3級風)，火箭橇發射后0.05 s、0.2 s、0.4 s、0.6 s、0.76 s時水平偏移如圖4所示，圖中圓圈代表橇體飛行位置，由圖可見在橇體發射后0.4～0.6 s，橇體的水平偏移最大達到0.06 m，但隨著橇體接近終點水平偏移又逐步縮小。

圖4 側向風速為5 m/s時火箭橇發射后的橇體偏移

圖5是發射后0.68 s、0.70 s、0.72 s、0.74 s、0.76 s時的橇體偏移。如果側向風速5 m/s時要求火箭橇在著靶瞬間其水平控制精度不大于0.01 m，則靶標與終點的距離應小于22 m。

圖5 側向風速為5 m/s時火箭橇發射后的橇體偏移

圖6是風速為5～10 m/s時，也就是從3級風到5級風情況下，橇體發射后0.76 s時的橇體水平偏移。可以看出當靶標設置在距離終點10 m處時，在風速小于7 m/s時，能夠保證水平控制精度不大于0.01 m。

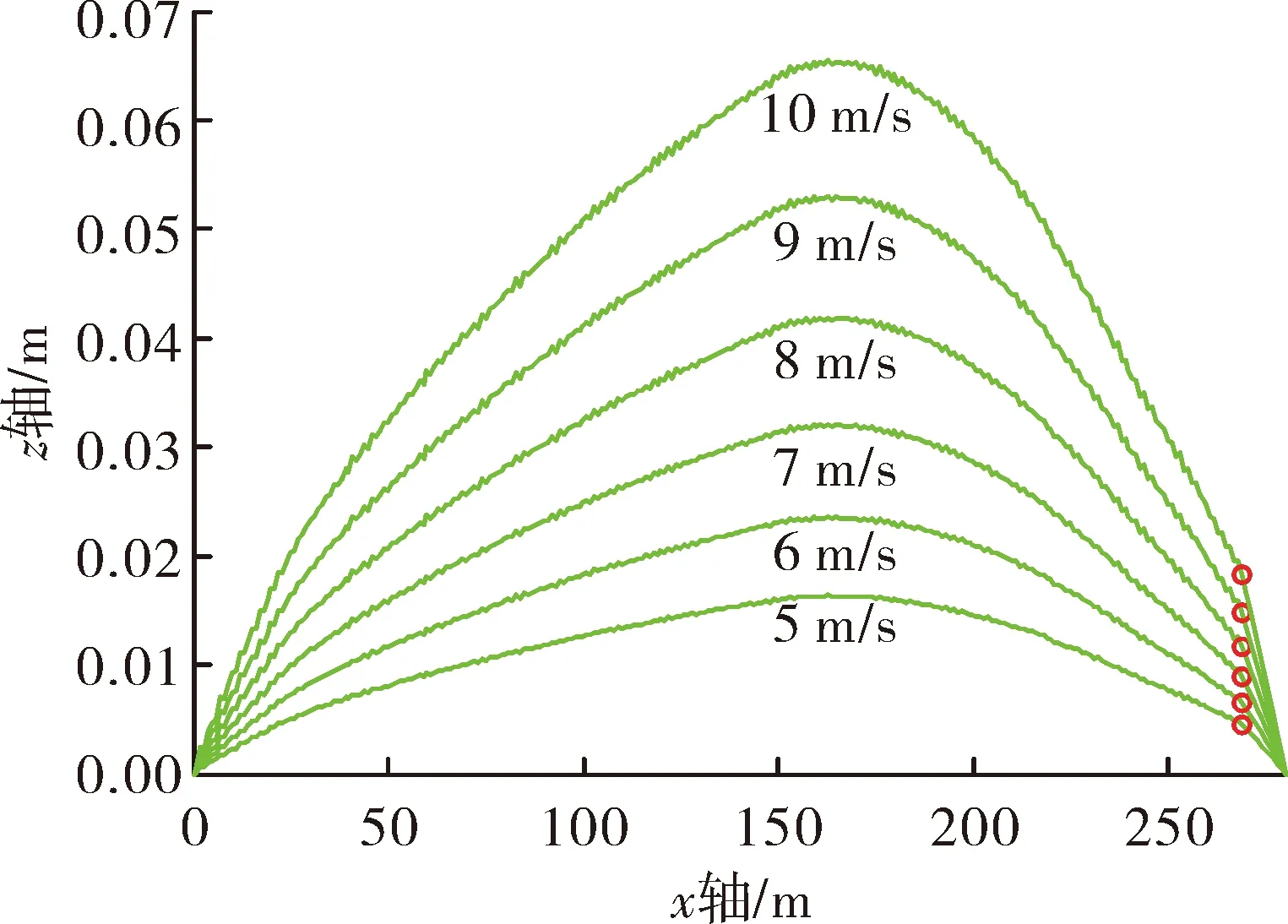
圖6 側向風速為5～10 m/s時火箭橇發射后0.76 s時的橇體偏移

綜合以上分析，為了保證火箭橇飛行末端的水平控制精度不大于0.01 m，側風速度應不大于7 m/s，同時靶標與終點距離應小于10 m。

4.2 懸索初始拉力對水平運動控制精度的影響

圖7繪制了側風vz=5 m/s時，不同初始拉力情況下，火箭橇發射0.5 s后橇體的水平偏移。圓圈對應橇體位置，橇體偏移最小的對應初始拉力T0=2 600 kg，橇體偏移0.05 m；橇體偏移最大的對應初始拉力T0=2 000 kg，橇體偏移0.75 m。

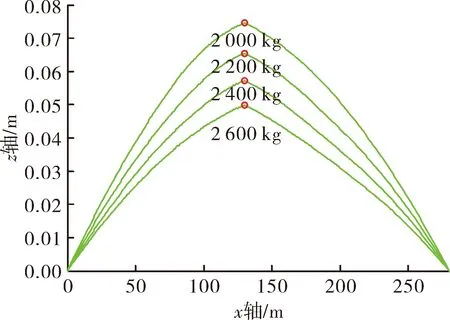
圖7 側向風速為5 m/s時，不同懸索初始拉力下火箭橇發射0.5 s時橇體的水平偏移

圖8繪制了側向風選為5 m/s時，不同初始拉力情況下，橇體發射后0.76 s，也就是飛行至距離終點約10 m處橇體的水平偏移，偏移最小的對應T0=2 600 kg，橇體偏移0.003 7 m；偏移最大的對應初始拉力T0=2 000 kg，橇體偏移0.006 9 m。

圖8 側向風速為5 m/s時，不同懸索初始拉力下火箭橇發射0.76 s時橇體的水平偏移

初始拉力大可降低橇體飛行過程中的水平偏移。但是初始拉力較高會提高系統的設計成本；綜合以上分析，在保證末端水平控制精度小于0.01 m情況下，設計初始拉力應大于2 000 kg。

4.3 懸索材料彈性模量對水平運動控制精度的影響

懸索的彈性模量與材料纖維粗細、盤結方式等因素有關，根據前期測試懸索材料的彈性模量會在一定范圍內變化，以下分析懸索彈性模量變化對橇體飛行控制精度的影響。圖9是彈性模量E=2.0×109Pa/m、3.4×109Pa/m、5.0×109Pa/m、6.5×109Pa/m時，初始拉力T0=2 400 kg，火箭橇發射0.5 s后橇體的水平偏移，可見偏移量差別也不大，約為0.057 m。

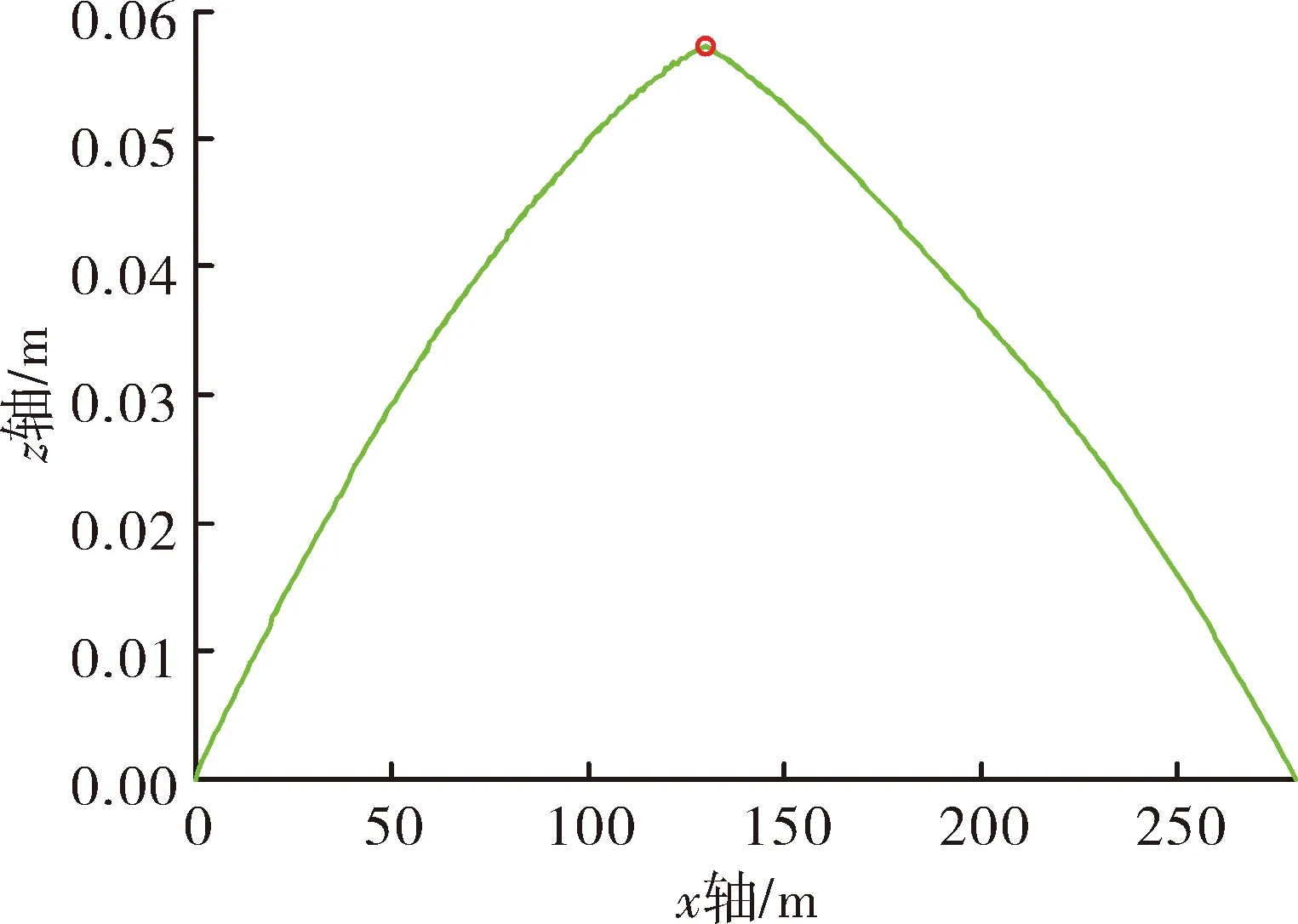
圖9 不同懸索彈性模量條件下橇體的水平偏移

所以當初始拉力較大時，懸索彈性模量差異對橇體的水平偏移影響可以忽略。

5 結論

利用Newton法對懸索進行3D運動建模，并結合橇體運動建模進行有限元仿真計算，分析了側風、初始拉力和懸索彈性模量等參數對橇體水平運動控制精度的影響；結果表明，監測試驗場地的實時風速，提高懸索初始拉力都有利于減少橇體運動的水平偏移。2018年年底進行的某型超音速懸索火箭橇飛行試驗結果表明，本方法計算得到的橇體水平偏移數據與現場測試結果相吻合，說明方法的有效性。