運(yùn)用“基本圖形”提高幾何解題能力的策略探究

摘要：在中考中幾何的證明與計(jì)算一直考查學(xué)生數(shù)學(xué)綜合解題能力一種重要題型，而我們的學(xué)生普遍存在幾何解題能力薄弱，幾何解題思路形成障礙，教師教學(xué)忽視對(duì)學(xué)生幾何解題思路的有效指導(dǎo)等問(wèn)題。我們知道研究幾何的重要方法就是研究幾何的基本圖形，本課題基于教師在平時(shí)幾何教學(xué)中，通過(guò)對(duì)基本圖形和性質(zhì)的歸納總結(jié)，引導(dǎo)學(xué)生從復(fù)雜幾何圖形中分離并提取基本圖形，最后利用基本圖形來(lái)解決較為復(fù)雜的幾何問(wèn)題，從而提高學(xué)生的幾何解題能力和幾何思維能力。

關(guān)鍵詞：基本圖形;解題;探究

本文作者從以下方面展開對(duì)幾何基本圖形的研究：

一、 基本圖形的歸納和總結(jié)是有效提高幾何解題能力的前提

（一）通過(guò)概念定理教學(xué)，引導(dǎo)學(xué)生歸納提煉基本圖形

教師在幾何概念、定理、性質(zhì)教學(xué)中，要引導(dǎo)學(xué)生有意的歸納和總結(jié)與核心幾何知識(shí)緊密相關(guān)的定理型基本圖形，充分建立起基本圖形和性質(zhì)定理的關(guān)聯(lián)。在學(xué)生掌握基本圖形的同時(shí)，加深了對(duì)幾何知識(shí)的直觀理解，也培養(yǎng)了學(xué)生的反思習(xí)慣和歸納能力。

①定義型基本圖形——加深概念理解

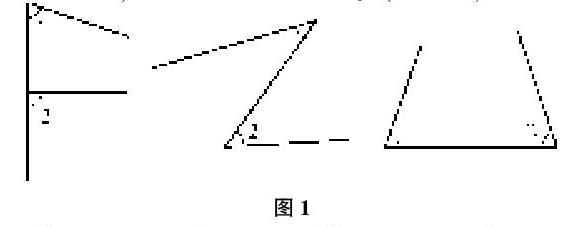
【舉例1】學(xué)習(xí)七下1.2同位角、內(nèi)錯(cuò)角和同旁內(nèi)角概念時(shí)，總結(jié)三種基本圖形。（如圖1）

第一種：同位角（F型）;第二種：內(nèi)錯(cuò)角（Z型）;第三種：同旁內(nèi)角（U型）;

通過(guò)把概念轉(zhuǎn)化為基本圖形，讓學(xué)生加深理解，再做復(fù)雜圖形中找角的練習(xí)，就可以轉(zhuǎn)化為找相應(yīng)的基本圖形，可以快速準(zhǔn)確地找到。

【舉例2】學(xué)習(xí)九上4.3相似三角形概念時(shí)，歸納六種基本圖形。（如圖2）

通過(guò)總結(jié)歸納六種相似三角形的基本圖形，可以加深學(xué)生對(duì)于圖形中邊和角的對(duì)應(yīng)關(guān)系，學(xué)生可以在一些復(fù)雜的相似三角形圖形中快速準(zhǔn)確地找到相似三角形。

②定理型基本圖形——促進(jìn)性質(zhì)理解

在幾何教學(xué)中，把課本核心的定理以基本圖形的形式體現(xiàn)出來(lái)，讓學(xué)生以直觀的幾何圖形來(lái)掌握定理，讓文字語(yǔ)言、圖形語(yǔ)言和符號(hào)語(yǔ)言有機(jī)結(jié)合。加深學(xué)生對(duì)于定理的理解，促進(jìn)學(xué)生對(duì)于定理的記憶。

【舉例3】學(xué)習(xí)九上3.3垂徑定理和3.4圓心角定理時(shí)，總結(jié)出基本圖形，加深直觀理解。（如圖3）

通過(guò)總結(jié)基本圖形，不僅能夠使學(xué)生知道垂徑定理和圓心角定理的內(nèi)容，同時(shí)也能使學(xué)生對(duì)于該定理的推理過(guò)程有直觀顯性的理解載體，由基本圖形構(gòu)建知識(shí)網(wǎng)絡(luò)，提高學(xué)習(xí)的效率，鍛煉學(xué)生幾何思維能力。

【舉例4】學(xué)習(xí)九下2.2切線長(zhǎng)定理時(shí)，總結(jié)出基本圖形。（如圖4）

通過(guò)總結(jié)基本圖形，不僅能夠使學(xué)生知道切線長(zhǎng)定理的內(nèi)容，更能使學(xué)生知道和理解該定理的證明過(guò)程，以及由此基本圖形推導(dǎo)得出其他結(jié)論。

教師在幾何教學(xué)中，要重視在教學(xué)核心基本定理時(shí)，引導(dǎo)學(xué)生總結(jié)歸納相應(yīng)的基本圖形，用幾何語(yǔ)言來(lái)表述定理，滲透這種理解、記憶幾何定理的方法，提高學(xué)生解決幾何問(wèn)題的能力。

（二）通過(guò)典例組圖教學(xué)，促使學(xué)生構(gòu)造積累基本圖形

①典例型基本圖形——簡(jiǎn)化思維過(guò)程

在幾何教學(xué)中，把教材及教學(xué)用書中經(jīng)常出現(xiàn)地能反映核心知識(shí)的例題、重要結(jié)論所蘊(yùn)含的圖形進(jìn)行歸納提煉積累，在解決幾何問(wèn)題中可以幫助簡(jiǎn)化思考過(guò)程，快速形成解題思路。

【舉例5】學(xué)習(xí)九上4.5相似三角形的性質(zhì)及應(yīng)用（3）作業(yè)題5：有一塊三角形余料ABC，它的邊BC=120mm，高線AD=80mm。要把它加工成正方形零件，使正方形的一邊在BC上，其余兩個(gè)頂點(diǎn)分別在AB，AC上。求加工成的正方形零件的邊長(zhǎng)。（如圖5）

這個(gè)基本圖形用到相似三角形對(duì)應(yīng)邊上的高之比等于相似比的性質(zhì)，圖形比較典型，涉及的知識(shí)也是相似三角形的重要性質(zhì)，學(xué)生熟練掌握這個(gè)圖形與性質(zhì)，能夠簡(jiǎn)化解決類似幾何問(wèn)題的思考過(guò)程。

【舉例6】在研究核心幾何問(wèn)題時(shí)，經(jīng)常出現(xiàn)（如圖6）所示的典型圖形，所涉及的知識(shí)點(diǎn)也是幾何的核心知識(shí)點(diǎn)。通過(guò)這類典型性幾何基本圖形的研究，可以使學(xué)生的解題形成典型性思維塊。

如圖6.1，結(jié)論是EF=BE+DF;它的證明方法具有典型性，需要旋轉(zhuǎn)變化、分散線段集中以及全等三角形的知識(shí)或者截長(zhǎng)補(bǔ)短的輔助線添法。

如圖6.2，三等直角基本圖形，形成左右兩個(gè)相似三角形，得到成比例線段，此圖應(yīng)用非常廣泛。

②組合型基本圖形——深化知識(shí)聯(lián)系

結(jié)合教材中出現(xiàn)的習(xí)題，以及有些常見的基本圖形不是單一型的，而是由若干個(gè)定理型基本圖形組合而成的，通過(guò)這些常見的組合型基本圖形的研究和提煉，不僅可以簡(jiǎn)化學(xué)生的解題思路，而且可以加強(qiáng)知識(shí)之間的聯(lián)系。

【舉例7】將若干個(gè)簡(jiǎn)單常見的概念定理型基本圖形結(jié)合在一起，形成一系列組合型基本圖形庫(kù)，舉例如圖7。

如圖7.1，是一個(gè)常見的組合型基本圖形，主要涉及平行線和角平分線的組合，得到等腰△ADE。

如圖7.2，也是一個(gè)非常廣泛的組合型基本圖形，涉及等邊三角形和全等三角形。

如圖7.3，條件是任意三角形兩條高線，并連接兩個(gè)垂足所形成的基本圖形，本圖是相似三角形“斜A型”和“斜X型”的組合圖形，共有8對(duì)相似三角形，很多幾何問(wèn)題經(jīng)常涉及此圖形。

（三）通過(guò)變式拓展教學(xué)，促進(jìn)學(xué)生透徹理解基本圖形

通過(guò)基本圖形的變式拓展學(xué)習(xí)，能使學(xué)生加深對(duì)基本圖形和性質(zhì)的靈活應(yīng)用，既讓學(xué)生經(jīng)歷體會(huì)到從“特殊到一般”的數(shù)學(xué)思想，又充分培養(yǎng)學(xué)生的幾何探究能力，另外運(yùn)用變式訓(xùn)練可以有效提高基本圖形的利用，有效培養(yǎng)學(xué)生的綜合思考能力，讓學(xué)生體會(huì)到形式改變，本質(zhì)不變的探究方法。

【舉例8】將圖7.2的基本圖形，改變條件，繞點(diǎn)B進(jìn)行旋轉(zhuǎn)任意角度，仍舊可以得到△ABE≌△CBD（如圖8.1）

變式1：將兩個(gè)有公共頂點(diǎn)的等邊三角形變成兩個(gè)有公共頂點(diǎn)的等腰直角三角形（直角頂點(diǎn)為公共頂點(diǎn)）仍舊可以得到△ABE≌△CBD（如圖8.2，8.3）

變式2：將兩個(gè)三角形變成兩個(gè)頂角相等的有公共頂點(diǎn)額等腰三角形（頂角為公共頂點(diǎn)），仍舊可以得到△ABE≌△CBD（如圖8.4）

通過(guò)對(duì)基本圖形進(jìn)行變式拓展研究，讓學(xué)生在進(jìn)一步加深對(duì)基本圖形的認(rèn)識(shí)的同時(shí)，又促使學(xué)生發(fā)現(xiàn)基本圖形所反映的性質(zhì)的本質(zhì)屬性，提煉出最本質(zhì)的基本圖形（圖8.4），完善了核心圖形。

【舉例9】將圖6.1的基本圖形，改變條件，將正方形改成等腰直角三角形其他條件不變，（如圖9.1），線段BM、MN、NC之間的關(guān)系發(fā)生了改變，變成了BM2+CN2=MN2，證明思路仍舊是利用旋轉(zhuǎn)變換，把三條線段集中在一個(gè)三角形中。（如圖9.2）

變式1：將正方形ABCD改成：在四邊形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°。E，F(xiàn)分別是BC，CD上的點(diǎn)，且∠EAF=60°。探究圖中線段BE，EF，F(xiàn)D之間的數(shù)量關(guān)系。（如圖9.3）

類似旋轉(zhuǎn)變換方法，仍舊可以得到EF=BE+DF。

變式2：進(jìn)一步改變條件：如圖9.4，只滿足AB=AD，∠B+∠D=180°。且∠EAF=12∠BAD，三個(gè)條件。上述結(jié)論EF=BE+DF是否仍舊成立？通過(guò)旋轉(zhuǎn)變換仍舊可以證明結(jié)論成立。

通過(guò)兩個(gè)變式，把基本圖形6.1所滿足的條件進(jìn)行了一般化，只要滿足變式2的三個(gè)條件，就可以得到結(jié)論成立。

在利用基本圖形提高幾何解題能力中，通過(guò)對(duì)基本圖形變式拓展研究，培養(yǎng)學(xué)生透徹理解圖形本質(zhì)特征，提煉基本圖形要滿足的本質(zhì)條件，幫助學(xué)生利用較少時(shí)間，解決典型變式，有效提高幾何問(wèn)題的解決能力和幾何思維能力。

二、 基本圖形的提取和運(yùn)用是有效提高幾何解題能力的方法

（一）通過(guò)簡(jiǎn)單顯性圖形教學(xué)，培養(yǎng)學(xué)生快速提取基本圖形能力

有些簡(jiǎn)單的幾何圖形，非常容易就可以發(fā)現(xiàn)蘊(yùn)含著的基本圖形，那么就要求學(xué)生能夠快速準(zhǔn)確地找出基本圖形，并形成解題思路。此類問(wèn)題面向不同層次學(xué)生都可以掌握。

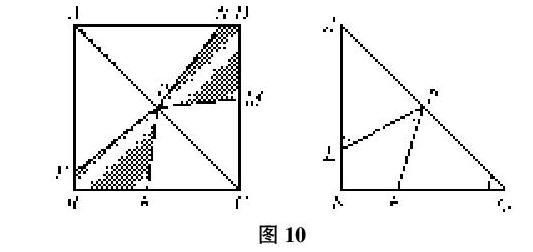
【舉例10】如前面所述：2013年杭州市中考題

根據(jù)題目中的條件，并觀察圖形，我們可以快速地發(fā)現(xiàn)“三等角”基本圖形（如圖10），從而得到△APE∽△CFP，迅速解決前面兩個(gè)小題。

（二）通過(guò)復(fù)雜顯性圖形教學(xué)，培養(yǎng)學(xué)生分解提煉基本圖形能力

有些較為復(fù)雜的幾何問(wèn)題，由于圖形較為復(fù)雜，不容易直接提煉出基本圖形，這時(shí)要重現(xiàn)圖形的產(chǎn)生過(guò)程，抓住重要核心條件，并根據(jù)重要條件進(jìn)行分解、聯(lián)想最后提煉出若干個(gè)基本圖形。

【舉例11】2014年杭州市中考題

已知AD∥BC，AB⊥AD，點(diǎn)E、F分別在射線AD，BC上，若點(diǎn)E與點(diǎn)B關(guān)于AC對(duì)稱，點(diǎn)E、F關(guān)于BD對(duì)稱，AC與BD相交于點(diǎn)G，則（）

A. 1+tan∠ADB=2

B. 2BC=5CF

C. ∠AEB+22°=∠DEF

D. 4cos∠AGB=6

根據(jù)題目中的條件和圖形，我們可以分解并提煉出基本圖形“同側(cè)公共邊解Rt△”（如圖11），從而通過(guò)解兩個(gè)Rt△，快速形成解題思路。

（三）通過(guò)局部隱性圖形教學(xué)，培養(yǎng)學(xué)生嘗試構(gòu)造基本圖形能力

有些幾何問(wèn)題，圖形中沒有非常明顯的基本圖形，只有局部圖形，這時(shí)要通過(guò)挖掘圖中的重要（核心）條件，進(jìn)行熟練嘗試和比照相關(guān)的基本圖形，通過(guò)添加輔助線來(lái)構(gòu)造熟悉的基本圖形，從而形成解題思路。

【舉例12】2014年拱墅區(qū)九年級(jí)中考模擬試卷

如圖12，已知第一象限內(nèi)的點(diǎn)A在反比例函數(shù) y=1x上，第二象限的點(diǎn)B在反比例函數(shù)y=kx上，且OA⊥OB，sinA=33，則k的值為（）

如圖12，根據(jù)通過(guò)重要條件直角，通過(guò)添垂線，構(gòu)造“三等直角”基本圖形，馬上形成解題思路。

【舉例13】2014年拱墅區(qū)九年級(jí)中考模擬試卷

如圖13.1，在直角坐標(biāo)系中，點(diǎn)P（3，3），兩坐標(biāo)軸的正半軸上有M、N兩點(diǎn)，且∠MPN=45°，則△MON的周長(zhǎng)等于。

如圖13.2，根據(jù)條件45°，嘗試構(gòu)造如圖6.1基本圖形，迅速得到此圖結(jié)論MN=EM+FN。

【舉例14】2009年杭州中考

如圖，在菱形ABCD中，∠A=110°，E，F(xiàn)分別是邊AB和BC的中點(diǎn)，EP⊥CD于點(diǎn)P，則∠FPC=（）

A. 35°B. 45°C. 50°D. 55°

本題涉及的圖形是一個(gè)局部的隱性圖形，要形成解題思考，關(guān)鍵是抓住本題的核心條件：中點(diǎn)和垂直，聯(lián)系基本圖形，添加輔助線，構(gòu)造基本圖形。（如圖14.3，全等三角形基本圖形，如圖14.4，直角三角形斜邊上中線基本圖形）。

綜上，運(yùn)用基本圖形尋找?guī)缀谓忸}思路，提高學(xué)生幾何解題能力是一種有效的方法，為學(xué)生的幾何解題提供了一種思維方式，讓學(xué)生體會(huì)到解決幾何問(wèn)題時(shí)有規(guī)律和方法可循的。

本文筆者通過(guò)分析學(xué)生幾何解題存在問(wèn)題的原因，提出了培養(yǎng)學(xué)生運(yùn)用“基本圖形”提高幾何解題能力的課題。研究了根據(jù)幾何基本圖形的分類運(yùn)用多種教學(xué)形式進(jìn)行歸納和總結(jié)的策略：基本圖形解題和思路、基本圖形的歸納和總結(jié)、基本圖形的提取和運(yùn)用。以此來(lái)激發(fā)學(xué)生學(xué)習(xí)幾何的興趣，獲得幾何問(wèn)題解題思路形成的經(jīng)驗(yàn)，提高較為復(fù)雜的幾何問(wèn)題的解題能力、問(wèn)題分析能力、邏輯推理能力。

參考文獻(xiàn)：

[1]林冬玲.重視基本圖形教學(xué)提高學(xué)生幾何學(xué)習(xí)的有效性[J].中學(xué)數(shù)學(xué)研究，2015（10）.

[2]柯偉賢.提煉基本圖形妙解幾何命題[J].中學(xué)數(shù)學(xué)研究，2015（8）.

[3]中華人民共和國(guó)教育部制定.義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2011年版）[M].北京：北京師范大學(xué)出版社，2012.

作者簡(jiǎn)介：

孫立剛，浙江省杭州市，浙江省杭州市蕭山區(qū)新桐初級(jí)中學(xué)。