基于核心素養下“三內角和定理”的反思

摘?要：三角形內角和定理等價于平行公理，對三角形內角和定理的教學歷來都是初中幾何教學的重要課程，教學過程中教師對教學的內容、教學現狀的把握和自我的定位有著重要的指導意義，研究旨在以“核心素養”教育理念為指導，以“三角形內角和定理”教學案例為例，對初中幾何數學教學提出教學思考和建議。

關鍵詞：三內角和定理;教學案例;初中數學教學

由羅增儒教授主講的“第五屆基于核心素養的數學教師專業發展高級研修班”于2019年8月12至14日在陜西師范大學雁塔校區舉辦。筆者作為學員第一次零距離聆聽大師的講解，深感幸運。因為這次的學習既不是學校的安排，也不是工作室的學習，純粹的是因為關注的中學數學參考公眾號，發現假期有個講座，抱著看看、豐富自己的態度來體驗的。經歷培訓后感受到了一個中學教師的魅力應該是怎樣的，感覺到對于今后自己的模樣看得見摸得著的感覺，也從心底感受到了數學教學文化的厚重感。借用羅增儒教授的話，我很贊同“數學家創造數學，數學教師創造數學的理解”這種觀點，從小我們有個數學家的夢想，現在明白數學家和數學教育家是很有區別的，這種界定要在心中明確，原來我是個搬運工。

培訓回來后，意識到自己處于數學教育改革的轉折點，也意識到區里舉行的核心素養教研并非是口號、是形式，而是數學教學所應追尋的更高階教學，理解并實行核心素養教學是現今教師專業發展的品質培養進階之路。就以羅增儒教授在8月14日上午《案例分析與教師專業發展》中提到了三角形內角和定理的一個教學案例，談談我的體會。

一、 三內角和定理的教學現狀

在文中，課堂教學前，教師布置給學生預習思考題：三內角和等于180°，你能用幾種方法證明這個結論？通過老師的引導和學生的思考不同的證法。

文中采取提問：三角形三個內角有什么關系？（當然，具體問的是數量關系），經過學生的測量與思考“發現”三內角和等于180°，從而受到啟發，在教師的幫助下完成證明。文中，通過老師的引導和學生的思考展現了學生7種不同的證法（詳請參閱文獻[1]），對于這7種方法是否都是通過學生的自主探索而得到的（學生會查資料），不得而知（畢竟課堂只有45分鐘，完全依賴于學生的創新難度大），但是這種前置探究的方式確實是一種新的教學嘗試。

文中采取“體驗”的方式設置特定的數學活動，如通過量角器“量一量”三內角再求和、利用“折紙”或者“剪拼”再觀察的方式對情景中的問題通過動手操作，主動認識和驗證研究對象的特征，從而獲得一些經驗，促進學生的數學領悟。

通過老師的引導和學生的思考呈現了7種不同的證法（詳請參閱文獻[1]），在教學中我們大多會發現學生用如下幾種方法：

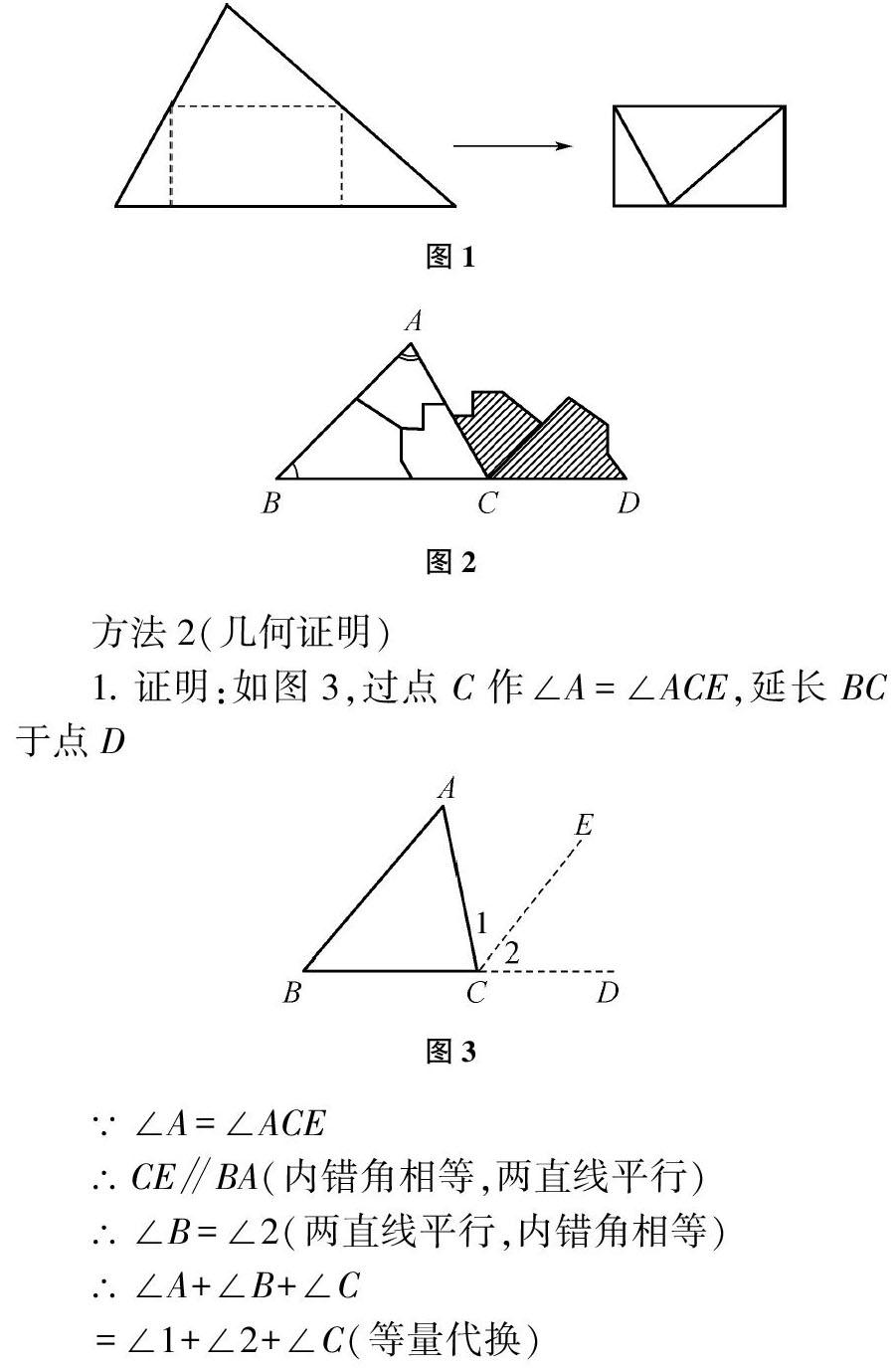
方法1（實驗操作）

1. 借助量角器測量給定三角形的三個內角再求和，估算和猜測得到“三角形三內角和等于180°”。

2. 通過手工操作的方式，將三角形沿如圖1的折痕翻折或者如圖2方式裁剪拼湊，操作后得到“三角形三內角和是一個平角”。

方法2（幾何證明）

1. 證明：如圖3，過點C作∠A=∠ACE，延長BC于點D

∵∠A=∠ACE

∴CE∥BA（內錯角相等，兩直線平行）

∴∠B=∠2（兩直線平行，內錯角相等）

∴∠A+∠B+∠C

=∠1+∠2+∠C（等量代換）

=180°（平角的定義）

2. 證明：如圖3，延長BC于點D，過點C作∠A=∠ACE（略）

思考：1采取先作∠A=∠ACE再延伸BC于點D，而2先延伸BC于點D再作∠A=∠ACE，自然而然有個問題，就是CE為什么會在∠ACE的內部？二者之間看似只是順序的改變，實則都是默認了外角大于內角的定理應用，而此時學生并未證明過該定理。所以這樣的描述方式有邏輯循環的嫌疑，我們應該提醒學生有這方面的思考，既為后面“三角形內角和定理的推論”作鋪墊，也培養了學生的思維嚴謹性。

改進：過點C作CE∥BA（CE的唯一性，避免了討論∠ACE的位置），延伸BC于點D。因此，也可以有圖3、圖4的輔助線添加方式。

3. 證明：如圖4，過點C作CD∥BA。

∵CD∥BA

∴∠A=∠1（兩直線平行，內錯角相等）

∠B+∠BCD=180°（兩直線平行，同旁內角互補）

∴∠A+∠B+∠C

=∠1+∠B+∠C

=∠B+∠BCD

=180°（等量代換）

4. 證明：如圖4，過點C作∠1=∠A。（略）

思考：3采取作平行線，注意取的哪個角（如圖取∠1）要說明，4采取在△ABC外部作已知角，二者利用都是利用前面所學的平行線的判定和性質這一知識解決問題，符合學生的實際。當點C在三角形內部或者外部時，仍成立，讀者可自行證明。

總結初中幾何證明步驟：（三段論）

第一步：將三個內角的和角轉化到一個新的角上

第二步：新的角是平角

第三步：三個內角的和等于180°

方法3（代數方程）

分析：如圖5，過點A作射線AD交BC于點D

則∠A=∠1+∠2，∠BDC=∠3+∠4=180°

由于我們討論的是三角形的內角和度數問題，即隱含三角形內角和是一個確定的值，既然學生已學一元一次方程，那么不妨將三角形內角和看作未知數，將證明題轉化為求方程的解的問題。

解：設三角形的內角和為x。則在△ABC、△ADB、△ADC中有：

∠1+∠B+∠3=x

∠2+∠4+∠C=x

∠BAC+∠B+∠C=x

∴∠1+∠B+∠3+∠2+∠4+∠C=2x

∠3+∠4+∠1+∠2+∠B+∠C=2x

∠3+∠4+∠BAC+∠B+∠C=x

180°+x=2x

解得：x=180°

二、 三內角和定理包含的核心素養

通過上面的案例展示和研究，我認為包含著邏輯推理、直觀想象、數學運算、數學抽象的核心素養。學生數形結合，通過圖形的測量、剪拼找到三內角和的關系或轉化途徑;角的分割、轉移、合并，產生求和式的拆項、交換和結合轉化為數量關系，在輔助線的添加過程中，變中含有不變。角的改變，而和不變。既如此，從方程角度思考，其和為不變量，則三內角和是一個定值，將未解決或較難的三角求和問題化為已解決或較易解決的加法運算或一元一次方程問題，這些都需要學生的運算能力。

三、 總結與建議

我們習慣從圖形上將角進行拆湊，卻容易忽視背后所對應量的值之間的加減運算關系，因為中間有了數形結合的思想方法，二者的銜接就是教師應該做的事情。作為教師，應該用我們的“雙眼”發現生活中的數學原型和數學應用，然后再“搬”到學生的面前，褪去“數學”的外套，讓學生零距離的感知“數學”，而不應該僅僅將數學教學落腳于學科知識和思想方法的傳授，現今的挑戰是如何抓住其背后包含的核心素養，幫助學生跨過數學思維的難關，成為用數學眼光觀察世界、用數學思維思考世界、用數學語言表達世界，成為一個擅觀察、勤思考，好交流的21世紀新學生。

參考文獻：

[1]陳恩忠.《三角形內角和定理》教學實錄與反思[J].初中數學教與學，2015（8）：17-18.

[2]羅增儒.點評：教師的設計要適合學生的實際[J].中學數學教學參考，1996（6）：20-22.

[3]鄧清，夏小剛.基于“三教”理念的初中幾何教學的認識與思考-以“三角形內角和定理”的教學為例[J].中國數學教育（初中版），2019（6）：22-24.

[4]龍顯邦.三角形內角和定理證明方法[J].數學學習與研究，2011（14）：97-98.

作者簡介：

沈艷，貴州省貴陽市，溪南高中。