Floquet-Bloch 理論在頻散曲線計算中的應用

童韞哲，范 軍，王 斌

(上海交通大學高新船舶與深海開發裝備協同創新中心海洋工程國家重點實驗室，上海200240)

0 引 言

頻散曲線在無損檢測、彈性目標聲散射機理及水聲傳播領域都有著廣泛用途[1-5]。在水下目標聲散射的研究當中，大量的實驗結果表明，水下目標的回波中除了容易解釋的幾何散射波以外，總是會出現一些不易解釋的非鏡面散射波，這些散射波實際上是在彈性體中傳播的波再輻射產生的[6]。所以計算彈性波的頻散曲線，了解彈性波的傳播規律，對水下目標聲散射的精細特征研究具有至關重要的作用。

對于頻散曲線的計算一般都歸結為特征方程零點的求解：

其中：k 為行波波數；ω 為角頻率。目前求解公式(1)的方法主要有三種：(1) 譜方法。該方法是一種較傳統的解析方法。譜方法數值插值的方法直接求解特征方程，具有計算量小，計算精度高的優點[7-11]。(2) 半解析半有限元(Semi-Analytical Finite Element,SAFE)法。該方法結合了有限元與解析解表達式的特點，只對波導截面進行建模，因此降低了計算模型的維度[12]。(3) 波有限元(Wave Finite Element,WFE)方法。該方法利用波導的周期性，通過建立一部分波導的有限元模型以及周期邊界條件獲得相應的剛度矩陣，并求解特征根[13]。

鑒于目前的商用有限元軟件的求解器能夠非常成熟地應用周期邊界條件求解特征方程，本文引入了波有限元(WFE)方法求解頻散曲線[13]。常規有限元方法無法實現無限長的波導建模，所以需要引入基于Floquet-Bloch 理論的周期性邊界條件。Floquet 理論是微分方程理論的一個分支，它是求解形如x (t ) = A (t )x (t )的周期性線性微分方程的一種方法，其中A (t )是周期為T 的分段連續周期函數，在固體物理學中叫做Bloch 理論。

1 Floquet-Bloch 理論在求解彈性體頻散曲線中的應用

有限元方法求解彈性體頻散曲線的關鍵在于利用Floquet-Bloch 理論將長度為L、高度為h 的有限長彈性體控制方程中的位移/振速寫成行波形式。省略時間因子eiωt，彈性體控制方程可以寫成：

其中：σ 是應力張量，u 是位移張量。將位移u 的解寫成平面波的形式：

公式(3)表示某一特定振動狀態f (y )沿著x 方向以行波的形式傳播，振動狀態只是y 的函數，在傳播過程中不發生變化，長度為L、高度為h 的計算單元示意圖如圖1 所示。

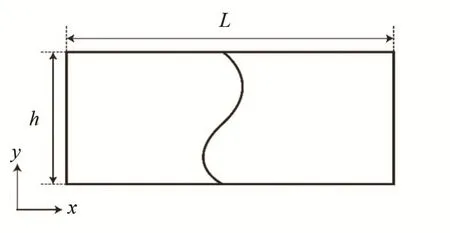
圖1 計算單元示意圖Fig.1 Schematic diagram of calculation cell

長度為L 的單元左邊位移和右邊位移存在如下關系：

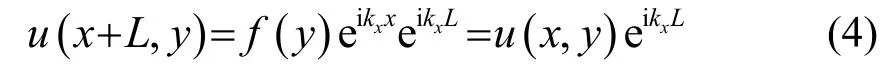
由于u 以行波方式沿著x 方向傳播，振動狀態與x 無關。二維無限長板可以近似認為沿x 方向周期為L 的周期性結構，利用Floquet-Bloch 理論，存在如下關系：

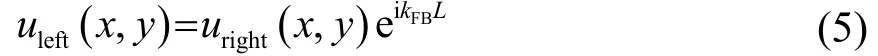
其中：kFB是Floquet-Bloch 理論的指數因子，kFB與x 方向的波數kx有如下關系：

詳細理論推導參見文獻[13]。

2 有限元計算結果與譜方法的對比

有限元在求解頻散曲線時的困難在于無法建立無限長的波導，Floquet-Bloch 理論實際上是對如圖1 所示的計算單元施加邊界條件以模擬無限長波導。COMSOL 軟件中Floquet 周期邊界條件模塊能夠實現這一功能，其公式為

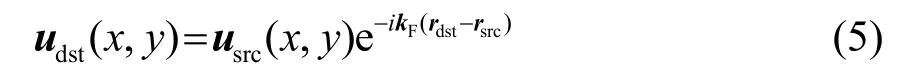
其中：usrc和rsrc是源邊界的位移和坐標；udst和rdst是目標邊界的位移和坐標，詳細信息參見文獻[14]。

在COMSOL 軟件中建立如圖2 所示的模型，在模型兩邊添加Floquet 周期性邊界條件，并輸入不同的行波波數kF，將有限長區域模擬成無線長波導，再利用特征頻率求解器求解相應kF所對應的特征頻率ω。

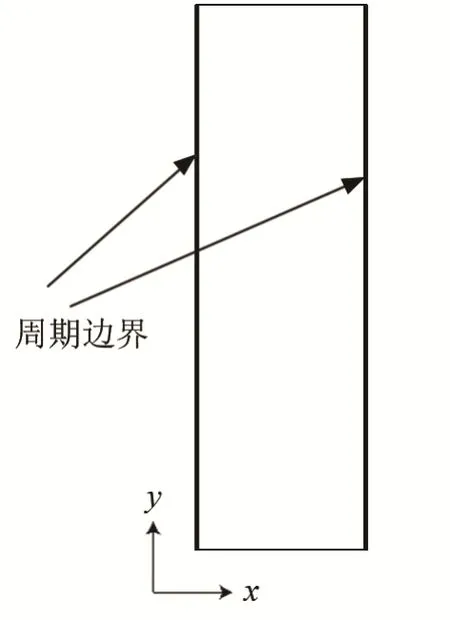
圖2 有限元計算示意圖Fig.2 Schematic diagram of finite element calculation

因為只考慮沿x軸傳播的行波，所以向量kF在y 軸投影為0，令其在x 軸的投影為kx。由式(6)可知，當n=1時，kx的取值范圍是0～2π /L，實際上kx取0～π /L最合理，具體情況會在下文討論。使用COMSOL 的搜根求解器可以求得kx滿足計算單元的特征方程所對應的所有特征頻率f，由特定的kx及與其對 應的特 征 頻 率f 可求得 對應 的 相速度Cp= 2π f/ kx。本文計算了兩邊真空的彈性平板頻散曲 線，參數為：ρ=7900 kg·m-3，縱波聲速CL=5940m·s-1，剪切波速CT=3 100 m·s-1，板的厚度h=40mm。

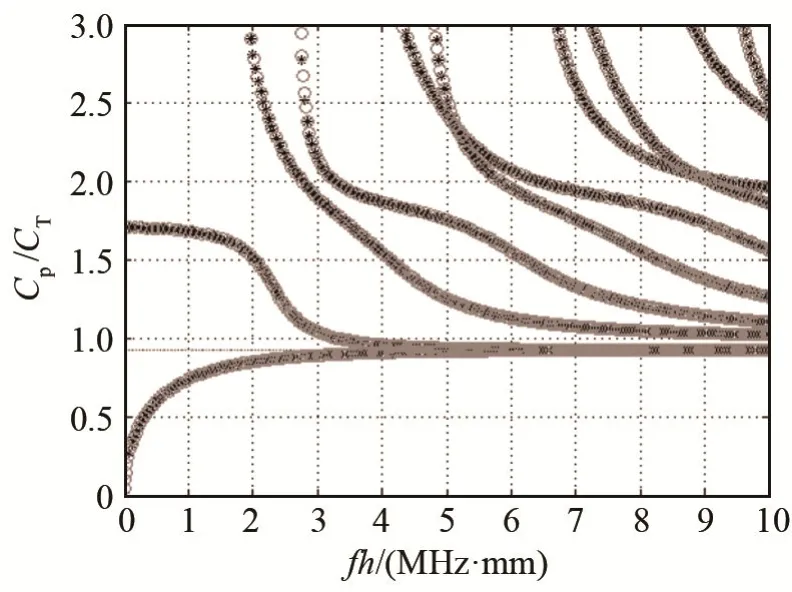
圖3 有限元與譜方法計算結果對比圖Fig.3 Comparison of calculation results of WFE method and spectral method

圖3 為有限元與譜方法[3]計算結果對比，橫坐標為頻率與板厚之積，縱坐標是相速度Cp與剪切波速之比。兩者吻合得非常好，從而證明了基于Floquet-Bloch 理論的有限元建模方法的正確性。

3 對于計算單元長度與高度之比值R的討論

選取合適的R(R 為計算單元的長度L 與高度h之比)對于計算結果至關重要。本文所提到的方法是用Floquet-Bloch 周期邊界條件模擬無限長的情況，所以存在一定的局限性，這一局限性主要體現在R 的大小與計算結果的關系。

圖4 是相同計算參數、不同R 值的計算結果，紅線分割了計算結果的有效區和無效區。由式(4)中 eikxL的周期性和對稱性可知波數kx必須滿足：

因此，kx所對應的特征頻率f 和相速度Cp必然滿足：

對公式(7)乘以厚度h，經過變換可以得到相速度pC 與頻率必須滿足：

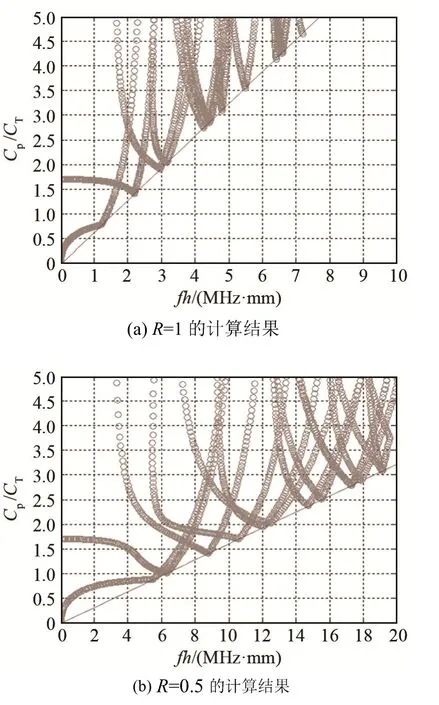
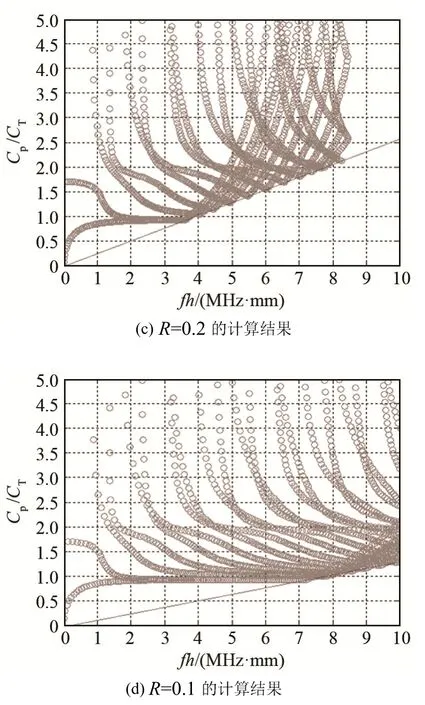
圖4 不同R 計算結果對比Fig.4 Comparison of calculation results of WFE method for different R values

由圖4(a)～4(d)可以看出：計算結果的有效區域隨R 的減小而增大，這一規律完全符合公式(13)。此外，根據經驗可知，當R=0.1 時計算結果較好，本文中的圖3 即是使用R=0.1 計算得到的結果。

4 結 論

本文簡要闡述了Floquet-Bloch 理論及其在頻散曲線計算上的應用。在此基礎之上，分析了其計算結果的局限性，為將此方法進一步應用于更加復雜的計算奠定了基礎。

本文得到以下主要結論：

(1) 利用基于Floquet-Bloch 理論的周期性邊界條件的有限元建模方法，能夠準確計算彈性體的頻散曲線；

(2) 通過周期性邊界條件將有限長彈性體近似成無限長波導存在一定的局限性，這一局限性體現在計算單元長度與高度之比R 對于計算結果正確區域的影響；

(3) 使用有限元法計算頻散曲線較之傳統的迭代法與譜方法有著操作簡單、不受波導形狀影響等優勢。