斷層破碎帶突水最小安全厚度的筒倉理論分析

孟凡樹，王迎超，焦慶磊,王月明，李朝陽

(1.深部巖土力學與地下工程國家重點實驗室(中國礦業大學)，江蘇 徐州 221116;2.中國礦業大學 力學與土木工程學院，江蘇 徐州 221116)

中國中西部地區山嶺眾多，地勢條件復雜，隨著中國地下工程建設的快速發展，修建穿越富水斷層破碎帶的隧道工程不斷涌現，隧道掌子面巖體由于高水壓、高地應力引發富水斷層破碎帶突水突泥災害時有發生.例如，宜萬鐵路馬鹿箐隧道和野三關隧道、吉蓮公路永蓮隧道等工程建設過程中，由于揭露富水斷層破碎帶發生多起突水突泥事故，造成了嚴重的經濟損失和人員傷亡[1].

近十幾年來，國內外學者對隧道施工過程中穿越富水斷層帶發生的突水突泥問題進行了大量研究.主要集中在兩個方面，一是突水災害賦存地質環境的研究.李曉昭等[4]提出斷層帶在開挖擾動條件下的受力變化作用，并對人工擾動作用下斷層的突水過程進行模擬分析，研究斷層的滲導水破壞機制.何發亮等[5]通過對國內外深長隧道突水突泥災害產生原因的充分調研，系統提出了深長隧道5種突水致災構造.張慶松等[6]研制了斷層破碎帶隧道突水突泥模型試驗系統，試驗揭示隧道開挖過程中及揭露斷層后的圍巖滲流壓力、應力應變、位移以及涌出物等特征參數的變化規律.二是對隧道周圍巖體破壞力學特征的研究[7].宋瑞剛等[9]根據總勢能原理，建立了穿越斷層破碎帶深埋隧道圍巖失穩尖點突變模型，推導出失穩的力學判據條件.張明聚等[10]采用巖體極限平衡理論，給出了突水臨界水壓力計算公式，并將其應用于翔安隧道突水風險的計算預測.張雨帆等[11]基于隧道滲流場的流固耦合原理，引入隧道穿越富水斷層帶設防長度概念，對隧道穿越富水斷層帶的加固范圍進行研究.王德明等[12]建立了斷層地質構造力學模型，通過時效損傷本構模型描述圍巖在動態破壞中的黏性和損傷特性，研究巖石體在突水突泥過程中的空間破壞形態.對于富水斷層破碎帶的突水突泥問題，因斷層破碎帶充填物由片狀角礫石為主組成的混合物，遇水不融化，發生突水突泥時呈流塑狀態，帶有壓力與碎屑流情況很像，因此,也有一些學者將其看成是“碎屑流”模型[13].其中于琳茗等[14]認為隧道掘進過程中，掌子面和碎屑流地層之間的距離小于最小安全距離時，在高水壓和高地應力的共同作用下，掌子面會由于經受不住其后方的水土壓力而發生碎屑流，即突水突泥.張志強等[15]自主研制“碎屑流發生”的模擬試驗裝置，“再現”碎屑流發生過程、形成條件，揭示碎屑流發生、發展規律，并分析碎屑流發生的影響因素.

由以上分析可以看出，目前對于斷層破碎帶突水的研究以模型試驗和數值模擬為主，少量的理論研究[14]也僅僅考慮掌子面后面的水壓或者直接把斷層破碎帶看成半無限體來分析臨界掌子面的土壓力，尚未考慮斷層破碎帶的長、寬對突水判據的影響.為此，本文首次將筒倉理論運用到斷層破碎帶突水研究中，結合極限平衡理論綜合分析了斷層破碎帶的寬度、長度對于隔水巖盤最小安全厚度的影響，推導出最小安全厚度的理論公式，為斷層破碎帶構造突水、突泥預測預防提供一種行之有效的計算方法，具有一定的理論研究意義與工程應用價值[2].

1 筒倉理論的基本原理

散體是大型離散宏觀粒子的混合體,散體物料不同于其他的氣體、固體和液體，具有自身獨特的特性，在筒倉中可以儲存任何的散裝物料[17].針對存儲這些散粒的筒倉壓力計算，最早的筒倉側壓力計算公式是由Janssen提出的,他推導的Janssen公式對此后的筒倉壓力計算產生了深遠的影響.直到今天，大多數國家筒倉設計規范所使用的側壓力計算公式還是以Janssen公式為基礎，Janssen公式做了以下假設[18]:1)筒倉內同一水平面上各點的豎向側壓力是相等的;2)散體任意一點的水平壓力與垂直壓力成正比;3)假定筒倉為無限深，且儲料不可壓縮.

根據上述假設求出靜態下不同深度的貯料壓力公式.如圖1所示,在距物料表面Z處取一厚度為dz的單元體進行受力分析[18]，其截面積為F,周長為C.物料單元體所受的垂直載荷與該層物料的自重及周邊承受的摩擦力相平衡，靜止平衡條件為

(PV+dPV)F-PVF+PWCdz-γFdz=0.

(1)

式中：PW為物料與倉壁摩擦力，kPa;PV為垂直方向上單位面積貯料壓力，kPa;γ為物料重度，kN/m3;C為筒倉橫截面周長，m.

式中:Ph為水平方向上單位面積貯料壓力，kPa;μ為物料與倉壁摩擦系數.

圖1 筒倉內物料薄層受力情況

設水平截面水力半徑ρ=F/C，Ph/PV=K為側壓力系數，PW/Ph=μ，代入式(1)結合初始條件z=0時，PV=0得

(2)

(3)

2 基于筒倉理論斷層破碎帶防突巖盤最小安全厚度

2.1 假設條件

張性或張扭性斷層受壓應力較小，內部結構松散，裂隙發育，主要由大小不規則的斷層角礫巖構成，當空隙不被后期物質充填膠結時，斷層富水性強，富水部位主要集中在破碎帶[6].因此，富水斷層破碎帶充填物既不是純固體，也不是氣體和液體，而是固、液、氣混合在一起的三相物質.本文主要研究未膠結的富水斷層破碎帶，筒倉存儲的物料散體特性基本一致.因此，將斷層破碎帶簡化成筒倉模型是合理可行的.

根據之前研究[8]，可以將斷層破碎帶引發的突水破壞模式簡化為相似的力學模型來分析.將富水斷層破碎帶位于隧道開挖工作面前方的簡化成巖塞模型，破壞形式是極限平衡條件下沿著防突巖墻發生直接的剪切破壞，即常說的拔塞效應，巖墻在沒有發生較大變形或開裂的情況，突然發生整體破壞[5].將富水斷層破碎帶位于隧道開挖輪廓線一側的簡化成梁破壞模型[5].假設條件如下：

1)將隧道掌子面與斷層破碎帶之間巖盤看成巖塞，巖盤為連續均勻的各向同性彈性體，符合小變形理論；

2)斷層破碎帶對臨界掌子面的作用力簡化成水壓力Q和地應力P分別作用；

3)張性或者順層錯動富水破碎帶時兩盤影響帶巖盤作為防突隔水層，壓性斷層富水破碎帶隧道施工由下盤向上盤施工，突破的隔水巖盤為壓性斷層主干隔水層，由上盤往下盤施工時突破的隔水層為上盤影響帶巖盤；

4)斷層破碎帶對隔水巖盤的側向壓力P通過將斷層破碎帶簡化成筒倉模型進行計算;

5)本研究針對斷層傾角比較大，規模較大的斷層破碎帶，并忽略水對巖盤的水合作用影響.

2.2 筒倉理論求解斷層破碎帶地應力P

對于富水斷層破碎帶在隧道施工掌子面前方臨界掌子面的壓力，通常將水土分開考慮，其中水壓力Q考慮成靜水壓力跟地下水位到隧道掌子面或者開挖輪廓線之間的高程差h成正比等于γwh，當斷層破碎帶與地表水相通時，為地表水位與隧道掌子面或者開挖輪廓線之間的高程差h等于γwh.

針對地應力P,之前學者很少考慮斷層破碎帶規模的影響，將斷層破碎帶看成半無限體來計算地應力，然后再乘以一個側向土壓力系數[14].然而，實際上斷層破碎帶的規模并沒有那么大，一般在幾十厘米到幾百米，尤其對于那些寬段小于100 m的，長度也不是很大的斷層破碎帶按照半無限體來計算側向土壓力會帶來相當大的誤差.本文基于筒倉理論，充分考慮斷層破碎帶的規模，尤其是斷層破碎帶寬度b的影響.

將整個斷層破碎帶看成一個大的深筒倉，斷層破碎帶四周的巖盤看成倉壁，斷層破碎帶的充填破碎巖塊和碎石就是貯料.結合筒倉模型和斷層破碎帶的實際情況，建立如圖2的力學受力模型，建立斷層破碎帶的平衡方程：

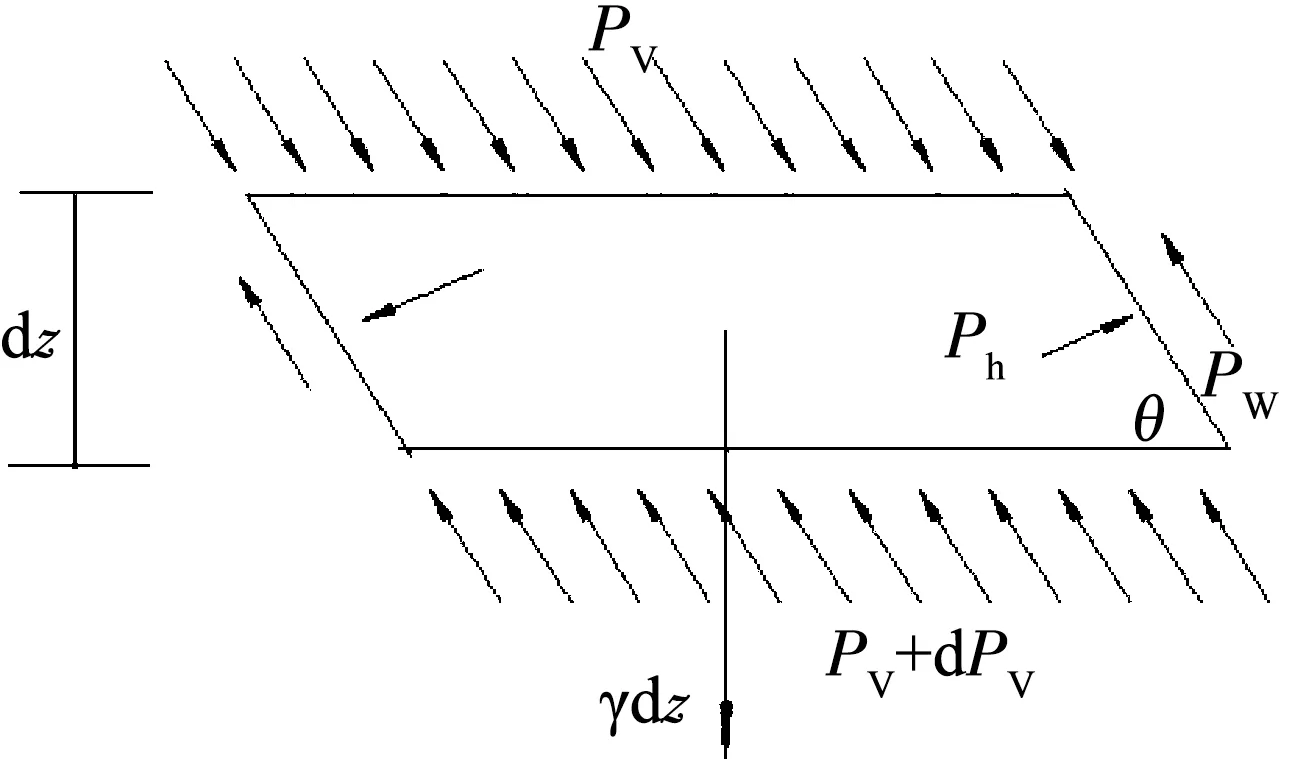
圖2 斷層破碎帶力學模型

(4)

dPVF+μ(Ph+0.5γbcosθ)Cdz-

γsinθFdz=0.

(5)

式中：F為截面面積，C為截面周長，令ρ=0.5bl/(b+l)為截面水力半徑，Ph/PV=K為側壓力系數，μ為摩擦系數，b為斷層破碎帶寬度，l為斷層破碎帶長度，γ為斷層破碎帶充填物的容重，θ為傾角，將ρ和K代入式(5)，整理得

(6)

求積分并代入初始條件z=0時，PV=0,計算可得

(7)

(8)

(9)

PV=γz(sinθ-2μcosθ)，

(10)

Ph=γz(sinθ-2μcosθ)/K.

(11)

再取θ為90°，則式(10)和(11)可以簡化成PV=γz，Ph=γz/K，顯然這是斷層破碎帶半無限大且垂直時的情況，也就是半無限大彈性地基地應力的一般解，是筒倉理論解的一種特殊情況.

2.3 斷層與隧道軸線正交突水模式及力學模型

未膠結的富水斷層破碎帶位于隧道掌子面前方的突水模式以及防突巖體力學模型[5]如圖3，4所示.基于極限平衡原理，由圖4所示的巖塞破壞力學模型，可以得到該模型下富水斷層破碎帶發生突水突泥時的力學極限平衡條件是作用在臨界掌子面上側向壓力的水平分量FS與巖盤阻力FH相等，即FS=FH.根據力學平衡條件便可求出隧道發生突水突泥時的最小安全厚度S.該模型下破壞首先發生在掌子面前上方，防突巖墻厚度最小的部分，然后地下水孕育發展最終防突巖墻發生整體破壞.

圖3 斷層破碎帶與隧道軸線正交的突水模式[5]

Fig.3 Water inrush pattern orthogonal to the tunnel axis in the fault fracture zone[5]

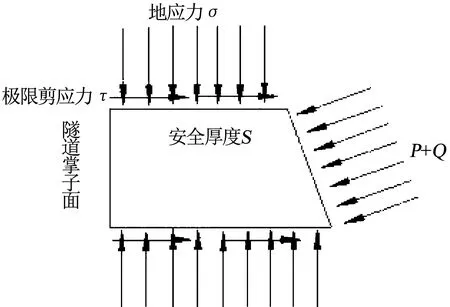
圖4 巖塞力學模型

水壓力和地應力作用在臨界掌子面垂直壓力的水平分量

(12)

防突巖盤的巖盤阻力FH由力學模型可以推出

(13)

根據力學平衡方程和筒倉理論結果得出巖塞力學模型下最小安全厚度的表達式如下

(14)

式中：γi為上覆第i層土的容重，kN/m3;γ為斷層破碎帶巖體容重，kN/m3;Hi為上覆第i層巖層的厚度，m;∑Hi防突巖墻中心的埋深，m;P為斷層巖盤所受地應力,kPa;Q為掌子面前方巖墻中心處的水壓力，kPa;φ′,c′分別為防突巖墻墻體的飽和內摩擦角和飽和黏聚力，kPa;θ為斷層破碎帶傾角，(°);μ為摩擦系數;D為隧道的直徑或等效直徑，m;z為計算點處的埋深，m.

考慮開挖擾動的影響，選擇爆破開挖方式，巖體受爆破開挖擾動損傷后阻水能力也大幅下降，可視為無阻水能力巖帶，即稱為爆破開挖擾動損傷帶.本文選用爆破開挖擾動損傷帶的取值為1.50 m[19]，則最小安全距離為S+1.5 m.

2.4 最小安全厚度影響因素分析

由式(14)可以明顯看出，隧道埋深、斷層破碎帶的寬度、斷層破碎帶水頭高度、容重還有防突巖體的物理力學性質均對最小安全厚度有影響.埋深、水頭高度、容重對最小安全厚度的影響基本上是線性的，隨著埋深、水頭高度、容重的增大而增大，與文獻[14]的結論基本一致.本文重點基于筒倉理論分析得到了斷層破碎帶的寬度，以及截面水力半徑ρ的影響.水力半徑與斷層破碎帶寬度和斷層延展長度有關，在不同延伸長度下，最小安全厚度隨斷層破碎帶寬度變化如圖5所示.可以看出，在斷層破碎帶延伸長度分別為500，1 000，1 500 m情況下，其他各參數取值如下：γ′=20 kN/m3，φ′=25°，c′=300 kPa，γ=18 kN/m3，μ=0.1，D=20 m，Q=3 500 kPa,H=500 m,K=1.2，θ=90°.隨著斷層破碎帶寬度的增大，最小安全厚度逐漸趨于一定值，即寬度和長度均無窮大情況.另外在延展長度較大的情況下，長度的變化對于安全厚度的影響較小.由圖5可以看出，在寬度小于500 m的情況下，最小安全厚度隨斷層破碎帶寬度變化特別明顯，差距很大，而在實際工程中斷層破碎帶寬度從幾十厘米到幾百米不等，正是處于變化特別大的范圍中，因而在確定最小安全厚度時，考慮斷層破碎帶寬度的影響特別有必要，而筒倉理論可以很好地實現這一點.

圖5 不同長度下最小安全厚度隨斷層破碎帶寬度變化

Fig.5 Curve of minimum safe thickness varying with the width of fracture zone at different lengths

2.5 與隧道軸線平行的斷層破碎帶突水模式和力學模型

未膠結的富水斷層破碎帶位于隧道開挖輪廓線外側的突水模式以及防突厚度力學模型[5]如圖6，7所示.富水張性斷層破碎帶位于隧道開挖輪廓線外的防突巖墻簡化成兩端固定的固支梁，固支梁的長度即為斷層破碎帶的長度L，斷層破碎帶兩端就是固定端兩端，梁上受均布荷載P+Q的作用.梁的截面取矩形截面尺寸為B×S,S為矩形的寬度，B為長度，隨斷層傾角的變化取值不同，不考慮防突巖墻的自重.

圖6 與隧道軸線平行的富水斷層破碎帶突水模式[5]

Fig.6 Water-rich fault water inrush pattern parallel to tunnel axis[5]

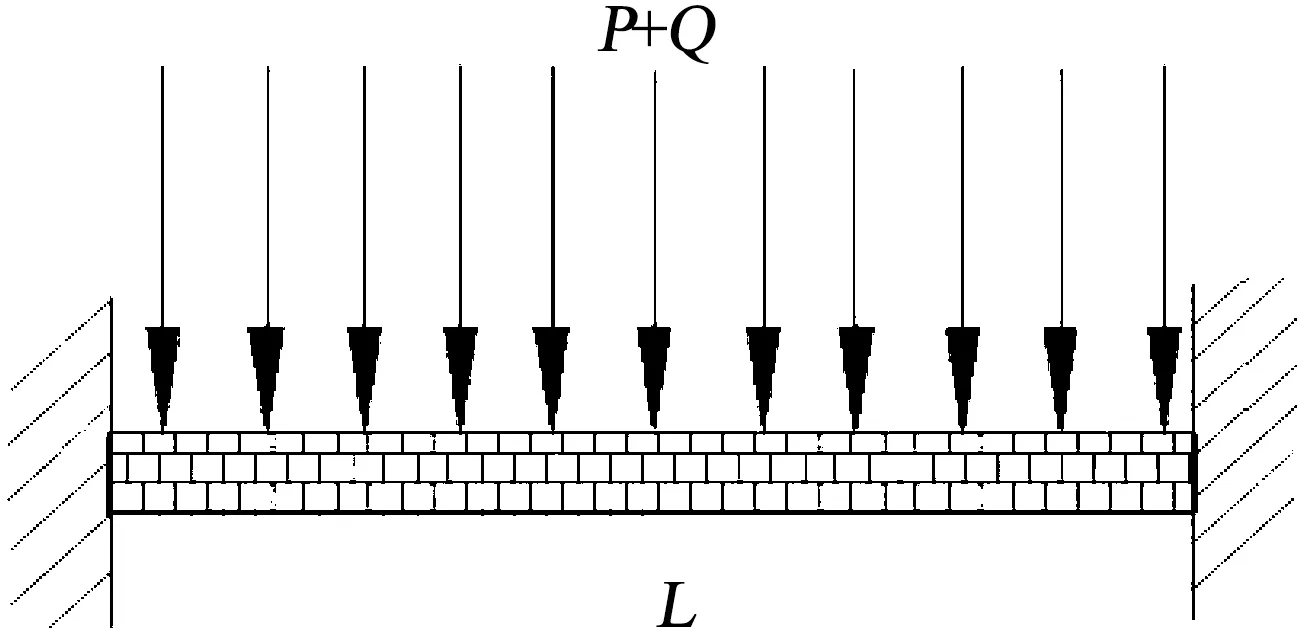
圖7 固支梁突水模型

根據力學知識可知，固支梁的最大彎矩和最大剪力均出現在兩端固定端[20]，即

(15)

固支梁按抗彎強度準則計算：

(16)

(17)

固支梁按抗剪強度準則計算：

(18)

(19)

式中：[σ]為巖體許用抗彎強度，[τ]為巖體許用抗剪強度，L為與斷層破碎帶平行隧道臨空面長度，S為巖墻安全厚度，其他參數同上文.因未考慮開挖擾動圈的影響，最小安全厚度需要乘以一個安全系數n,然后最小安全厚度要取按抗彎強度和抗剪強度計算的安全厚度數值中的較大值，這里只考慮未支護情況.隧道軸線與斷層破碎帶平行情況下工程中幾乎不會發生突水情況，因為在設計時取一個大一點的安全系數，即遠離斷層是完全可以做到的也不會增加大的成本.

3 工程案例

3.1 永蓮隧道工程應用

永蓮隧道隧址區地質構造發育，隧道出口段以砂巖、頁巖及灰巖為主，次生構造較為發育，隧道左側發育一條與隧道同向的大型斷裂帶F5，并以F5斷裂帶為主干，衍生F1～F4 4條次生斷層破碎帶，其中F2斷層破碎帶對隧道影響最顯著.斷層破碎帶巖體破碎-極破碎，采芯率為55%～65%，RQD<10，[fa0]=400 kPa.進口左洞在K91+313-364附近與F2斷層相交(設計線與地面線高差185 m).進口右洞在K91+389-425附近與F2斷層相交(設計線與地面線高差198 m)[12].永蓮隧道設計為雙向分離式隧道，隧道開挖斷面高度為9.06 m，寬度為12.6 m，單洞長約2.6 km，隧道平均埋深180 m，地下水位距離隧道拱頂約150 m，隧道進口施工至揭露F2斷層時發生大規模塌方、突水突泥災害.F2斷層與隧道軸線45°相交，傾向E，傾角84°，寬度15～35 m，查明延伸長度520 m，斷層破碎帶物質泥化后主要呈流塑狀態，看成Ⅵ圍巖，容重16 kN/m3，泊松比0.45，內摩擦角20°.正常圍巖段則主要以泥巖、頁巖為主，遇水不崩解可作為相對隔水層，可以看成是Ⅴ圍巖,對應圍巖的物理力學為：容重20 kN/m3，泊松比0.4，黏聚力150 kPa，內摩擦角25°，D=12.6 m，H=180 m,地下水位高度h=150 m，θ=84°，斷層長度L=520 m，寬度b=35 m，斷層泥飽和呈流塑狀態，摩擦阻力取μ=0.1，側壓力系數K取1.2，爆破開挖擾動距離取1.5 m，分別將數據代入式(9)和(13)得P=1 889 kPa,τ=1 829 kPa，Q=γwh=1 500 kPa,再將其代入式(14)得S=5.84 m加上擾動距離1.5 m,最終最小安全厚度為7.34 m.

顯然，當防突厚度接近7.34 m時，需要采取相應的措施防止突水，而永蓮隧道接近F2斷層破碎帶時并沒有做出相關應對措施，而實際工程結果證明，當掌子面揭露F2斷層后，隧道發生了多次大規模災害.

3.2 祁連山隧道工程應用

祁連山隧道位于祁連山冷龍嶺斷層褶皺帶，通過鉆探、物探及地表地質調繪，隧道共含有F6, F7等2條斷層破碎帶.F6斷層為逆斷層，其上盤、下盤分別為志留系下統板巖、二疊系砂巖.斷層帶以斷層角礫為主，且巖體較為破碎.隧道洞身通過F6斷層地段為DK336+050-140，長約90 m.F7斷層為逆斷層，斷層產狀為其上盤、下盤分別為志留系下統板巖、泥盆系砂巖.F7斷層屬冷龍嶺深斷裂，其于加里東早期或更早時形成，并在家里東晚期時受到強烈擠壓，致使活動期長，規模巨大.隧道洞身通過F7斷層地段為DK337+320-450，長約130 m.施工過程中預留了12 m的安全厚度，采取一些措施順利地通過了斷層破碎帶沒有發生突水突泥事故[16].根據地質資料，斷層破碎帶處隧道埋深750 m,水頭高度350 m,洞徑20 m寬，斷層面摩擦系數μ取0.1，側壓力系數K取1.2，開挖擾動距離取1.5 m,隧道巖盤處巖體容重20 kN/m3，摩擦角25°，內聚力300 kPa，斷層破碎帶處巖體容重18 kN/m3，斷層破碎帶傾角取90°計算.

用筒倉理論建立的模型和式(9),(13),(14)計算得到過F6斷層破碎帶寬度b=90 m的最小防突安全厚度8.52 m,通過F7斷層，斷層破碎帶寬度b=130 m時最小防突安全厚度9.66 m.而在洞室實際開挖過程中，取安全距離為12 m，采取相應的措施，安全通過了斷層破碎帶地段.在工程施工中安全距離往往需要理論值乘以大于1的安全系數n，取n=1.2則按照筒倉理論計算得到的理論值換成實際值得到10.22和11.59 m，和實際工程中的預留厚度12 m很接近，說明理論求解出的最小安全厚度具有一定的可靠性.

4 結論與展望

1)首次將筒倉理論引入到隧道斷層破碎帶突水的力學判據研究中，為未膠結的大傾角斷層破碎帶隧道突水、突泥最小安全隔水巖層厚度計算提供了一種新思路和方法.

2)分別建立了隧道軸線與富水斷層破碎帶正交和水平兩種情況下的力學模型，得到最小防突安全厚度的計算公式，考慮了斷層破碎帶寬度的影響，得到在斷層破碎帶寬度小于500 m，特別是200 m以內的情況下，斷層破碎帶寬度對于最小安全厚度的影響非常明顯的結論.

3)將研究成果應用于永蓮隧道和祁連山隧道工程，對理論計算結果與實際工程結果進行比較，與實際工程結果具有較好的一致性，證明了本文得到的力學判據具有一定的合理性和有效性.

4)本文Janssen公式推導過程中假定了垂直壓力與水平壓力之比K為一常數，而實際情況中K會隨著埋深高度而變化，目前還沒有成熟的理論結果，進一步研究可以考慮K的變化情況.