大理巖特征應力的加載速率效應研究

朱 俊,鄧建輝,黃弈茗,劉 濤,馬元軍

(1.水力學與山區河流開發保護國家重點實驗室(四川大學)，成都 610065； 2.四川大學 水利水電學院，成都 610065； 3.西北礦冶研究院，甘肅 白銀 730900)

巖石是一種包含如孔穴、微裂紋、節理等各種缺陷的材料.在外界荷載作用下，必然引起這些缺陷擴展、匯合，并產生新的微裂紋.巖石變形破壞與微裂紋的活動狀態密切相關，是細觀裂紋不斷擴展的宏觀結果.Bieniawski[1-2]按照不同應力水平下巖石內部微裂紋活動狀態的差異，將巖石的峰前應力-應變曲線劃分為4個階段，如圖1所示.階段Ⅰ：原生裂紋壓縮閉合階段;階段Ⅱ：線彈性階段;階段Ⅲ：裂紋穩定擴展階段;階段Ⅳ：裂紋非穩定擴展階段.各階段結束點對應的應力值分別為閉合應力σcc、起裂應力σci、損傷應力σcd和峰值應力σc.其中巖石的起裂應力σci(圖1中S點)和損傷應力σcd(圖1中T點)作為表征巖石內部裂紋擴展的兩個重要特征應力引起廣泛關注.

Martin等[3-4]研究了Lac du Bonnet花崗巖，發現其σci、σcd分別為單軸壓縮峰值強度的0.4～0.5倍和0.8倍；Everitt[5]發現巖石內部結構對其σci、σcd有較大影響；汪斌等[6]獲得錦屏大理巖的σci、σcd與σc比值范圍分別為0.38～0.52和0.82～0.86；彭俊等[7]研究了在圍壓和水壓作用下砂巖σci、σcd的變化，發現隨水壓增大，巖石的σci有逐漸增大的趨勢，而σcd和峰值應力σc逐漸減小，隨圍壓增大，其σci、σcd和σc均逐漸增大.起裂應力σci和損傷應力σcd的確定方法有多種，包括應力-應變曲線判定法、體積應變法、AE聲發射法、移動點回歸法等，但其精確性受到巖石類型、試驗方法等因素的影響[8-10].綜合各類確定方法發現，目前確定特征應力值多為試驗方法，數值模擬方法鮮有報道.

工程巖體受到荷載的變化速率對巖石的力學性能有較大影響，巖石荷載變化速率效應分析一直被廣泛研究.普遍認為，加載速率越高，巖石內部微裂隙來不及擴展、貫通，使其抗壓強度增加[11-15].也有學者發現在某些加載速率范圍內，巖石強度出現下降[16-17].總結以上研究成果發現，針對巖石特征應力的加載速率效應研究較少.另外，由于加載速率效應研究試樣個體數多，試驗重復性大，數值模擬方法將突破這一成本局限而成為一種便捷途徑.

為研究不同加載速率下脆性巖石的特征應力變化規律，設計了3種加載速率下大理巖的單軸壓縮試驗.采用體積應變法、聲發射法和黏結顆粒離散元(bonded particle model, BPM)數值方法(下文簡稱BPM模擬法)，確定其特征應力，通過對比分析驗證數值法的可靠性.并采用數值法模擬6種不同加載速率下的單軸壓縮試驗，綜合分析了大理巖特征應力的加載速率效應.

1 特征應力的確定

1.1 特征應力確定方法

巖石的起裂應力σci是裂紋穩定擴展的起始點，此時巖石內部的微缺陷(孔洞、微裂紋等)開始萌生、擴展.損傷應力σcd是裂紋非穩定增長對應的強度閾值.前一階段萌生、擴展的裂紋大量匯合、貫通，發生非穩定性擴展.為探究采用BPM模擬法確定σci、σcd的合理性并保證取值準確，本文采用體積應變法、聲發射法、BPM數值模擬法確定特征應力值.

1.1.1 體積應變法

對于常規單軸壓縮實驗，體積應變εv可通過測試近似計算，即

εv≈2ε1+ε2.

(1)

式中:ε1為橫向應變，ε2為軸向應變.

當外力超過巖石的起裂應力時，內部裂紋開始萌生、擴展，橫向應變和體積應變曲線開始偏離線性，該點對應的應力為起裂應力σci.當外力超過損傷應力時，內部裂紋匯合貫通，體積應變曲線出現拐點，該點對應的應力為損傷應力σcd(圖1).

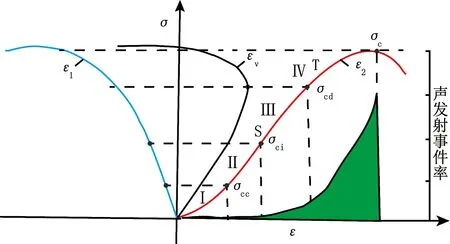
圖1 根據微裂紋發展劃分不同階段的應力-應變曲線

Fig.1 Stress-strain curves of different stages based on the development of micro-cracks

1.1.2 聲發射法

聲發射(AE)是材料內部能量迅速釋放而產生的彈性波.可以通過監測到的聲發射信號來判斷微裂紋的發展情況.Eberhardt等[8]研究指出，聲發射信號第1次明顯增加時的應力即為起裂應力σci，第2次突然躍起時的應力即為損傷應力σcd(圖1).聲發射特征參數中，考慮振鈴計數比較敏感，容易受到外界干擾，所以，多選用AE事件率和AE累計事件數，必要時結合幅值、能量曲線來研究特征應力.

1.1.3 數值法

顆粒流法是由Cundall P A和Strack O D L[18]在離散元理論基礎上提出的，在巖石損傷和細觀裂紋發展等方面應用廣泛.巖石宏觀破裂如斷裂破壞都是由于細觀結構的貫通，微觀裂紋的分析是研究破裂問題的根本.Diederichs等[19]運用離散元模擬花崗巖并分析其損傷破壞過程.Sharafisafa等[20]采用離散元研究了脆性巖石的裂紋萌生、延伸和貫通機制.

BPM模擬法可以監控巖石壓縮破壞過程中微裂紋數量增長過程和分布特征，其典型的微裂紋數增長情況如圖2所示，基于微裂紋數的BPM模擬法可以確定巖石的特征應力.在加載初期未出現微裂紋，此時巖石試件處于壓密和彈性階段.隨著應變增大，在E點后破裂開始出現并增加，此時的突變點E對應的應力即為巖石的起裂應力σci，微裂紋數量經過一段較平穩線性增加后，進入非線性增長階段，其突變點F對應應力即為巖石的損傷應力σcd.

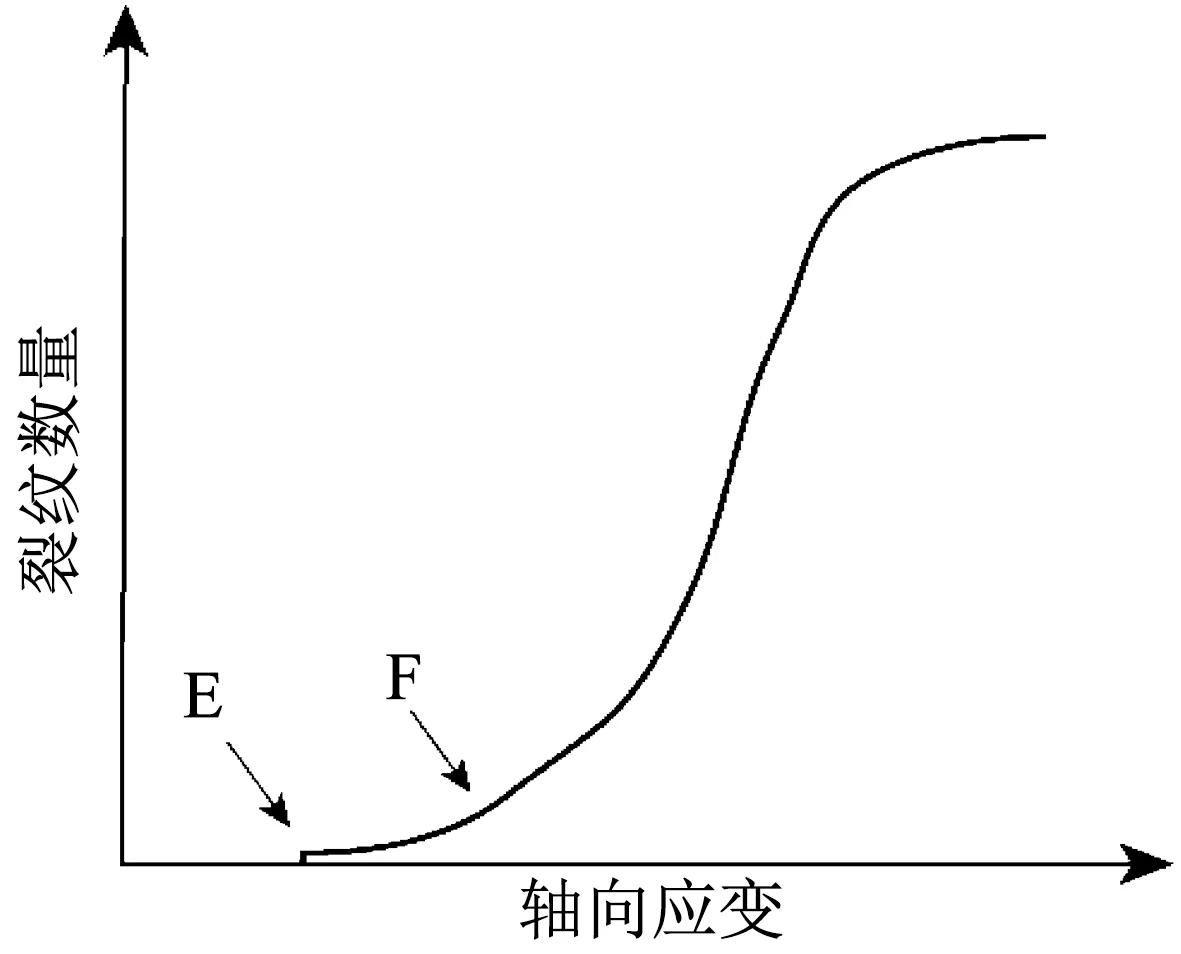
圖2 壓縮過程典型裂紋數量變化

Fig.2 Variation diagram of crack numbers during compression

1.2 試驗過程

試驗用大理巖取樣于四川省雅安市寶興縣，別名“蜀白玉”.采用X射線單晶衍射儀測定其礦物成分為方解石，達到99%以上.按照水利水電工程巖石試驗規范，加工成直徑50 mm，高度100 mm的標準圓柱體試樣，試樣兩端平行度和垂直度滿足規范要求.試驗加載速率控制為5×10-6，8×10-6，5×10-5m/s，每一加載速率下進行試驗的巖樣4個，共計12個.

為保證采用體積應變法和聲發射法獲得大理巖的特征應力，設計如圖3所示的試驗方案：采用MTS815型巖石力學加載系統和PCI-2聲發射信號采集系統記錄試驗過程中力學數據和聲發射數據，每個巖樣共布置8個Micro30高精度探頭，采用環向和軸向引伸計測定環向和軸向位移.各巖樣的物理力學參數如表1所示.

1.3 數值模擬過程

采用PFC2D軟件模擬大理巖單軸壓縮過程以確定其特征應力.PFC2D采用細觀力學參數表征顆粒及黏結的力學性質.在數值模型計算分析前，需進行大量的模型驗證工作，即通過不斷調整細觀參數，將計算得到的試樣宏觀力學參數與室內試驗結果對比.當計算結果與試驗結果基本接近或一致時，便可選擇該組細觀力學參數構建實際計算模型.

當采用表2所示細觀參數時，生成與試驗試樣尺寸一致的數值模型，如圖4所示.模型共計顆粒13 054個，顆粒間黏結采用平行黏結.

圖3 聲發射探頭和位移傳感器布置

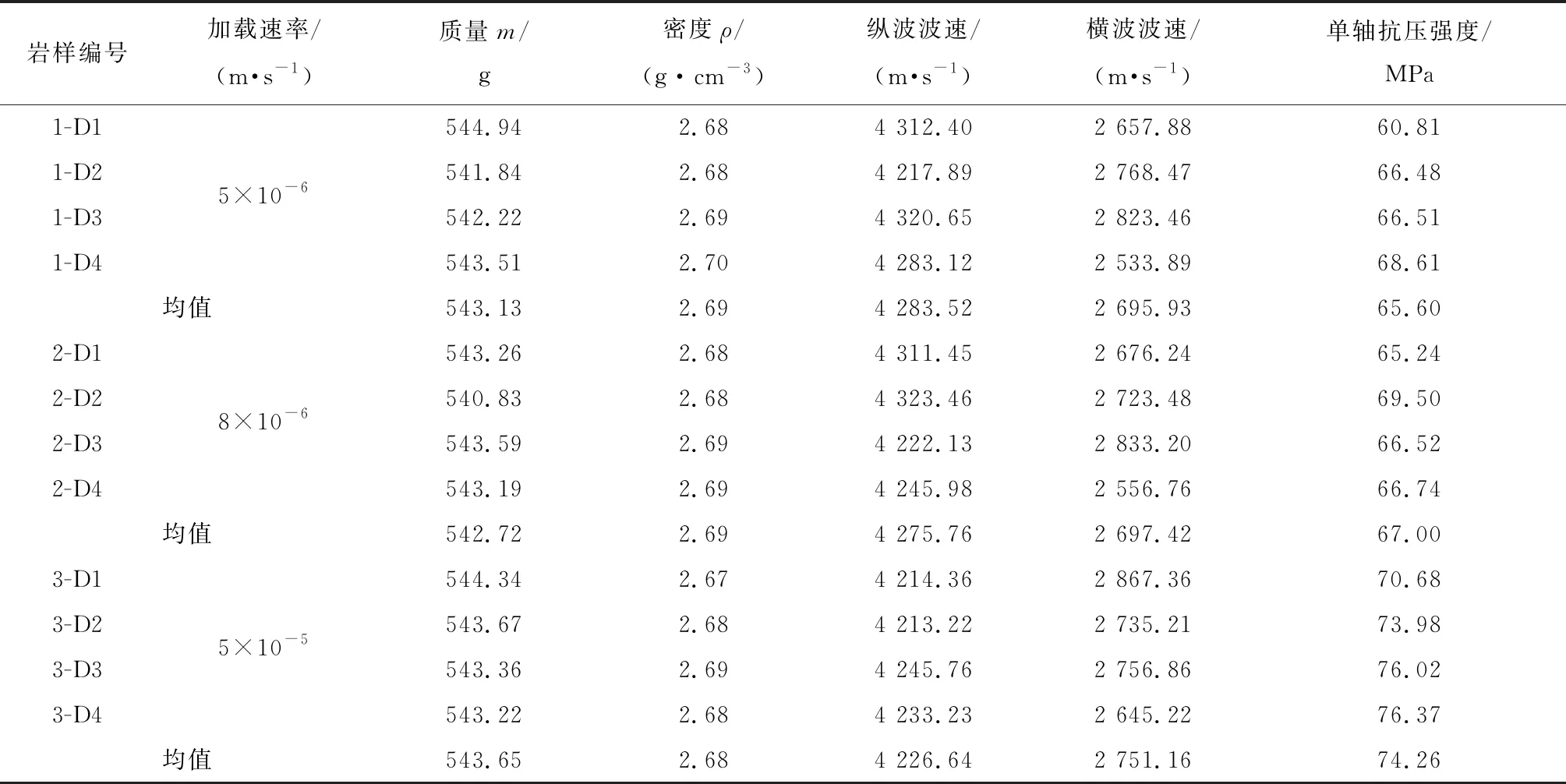
表1 巖樣物理力學參數

表2 模型細觀力學參數

圖4 PFC2D數值試件及局部放大圖

加載速率為5×10-5m/s時，數值模擬與室內試驗試樣(3-D2)的破裂面比較如圖5所示.限于篇幅，其余試樣對比不一一給出.可以看出，試驗巖樣和模擬巖樣主次破壞面均為剪切破壞面，試樣右下端部出現剪切破壞.

圖6為不同加載速率下試樣試驗與數值模擬應力-應變曲線對比.考慮巖樣個體差異性，選取每一加載速率下，與該組單軸抗壓強度均值最為接近且典型的巖樣作為數值模擬比較對象，選取巖樣分別為1-D2、2-D4、3-D2.由圖6對比可以看出，不同加載速率下模擬結果和試驗所獲得的應力-應變曲線基本吻合，表現在峰值強度、彈性模量、峰值應變等基本接近或一致.

圖5 模擬和試驗巖樣破裂特征對比

Fig.5 Comparison of failure characteristics between the simulated and test rock samples

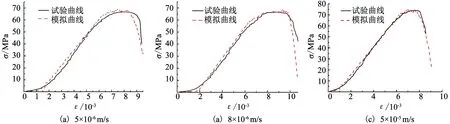
圖6 不同加載速率下模擬和試驗巖樣應力-應變曲線對比

不同加載速率下巖樣的試驗峰值強度和數值模擬峰值強度對比如圖7所示.可以看出，試驗用巖樣在5×10-6～5×10-5m/s加載范圍內表現出加載速率效應，其強度隨加載速率增大而增大.另外，試驗和模擬峰值強度隨加載速率變化趨勢基本一致，擬合曲線較為接近.

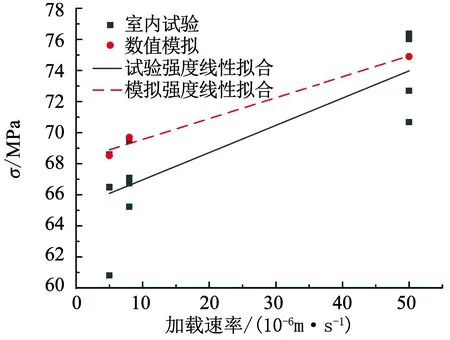
圖7 顆粒細觀摩擦系數折減后邊坡模型的位移場

Fig.7 Comparison of peak strength between test and numerical simulation of samples at different loading rates

通過對比應力應變曲線、破裂形態和峰值強度，發現PFC2D數值模擬結果與室內試驗結果較為接近，認為建立的數值模型較為可靠.

2 特征應力結果分析

2.1 試驗結果

室內試驗可以獲得各巖樣的力學數據和聲發射監測數據，限于篇幅，這里僅以加載速率5×10-5m/s的巖樣3-D2為例，說明特征應力確定的過程.

圖8為巖樣3-D2的壓縮變形曲線.在巖樣變形曲線中，橫向應變曲線偏離線性段的應力對應起裂應力σci(如圖8中的A點)，體積應變曲線的拐點對應應力即為損傷應力σcd.為準確確定拐點并保證擬合效果，通過對一定范圍內的數據進行擬合，得到擬合曲線的解析式，并利用Matlab軟件編程求得拐點的解析解，如圖8中B點所示.同樣，可以獲得所有巖樣的特征應力值.

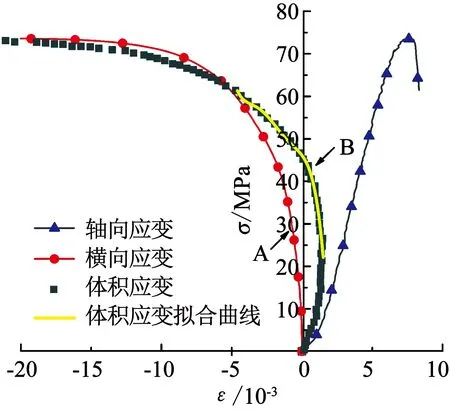
圖8 巖樣3-D2壓縮試驗過程變形曲線

Fig.8 Deformation curves of rock sample 3-D2 during compression test

圖9為巖樣3-D2的應力、AE事件率、AE累計數和時間的關系曲線.結合圖中的AE事件率和AE累計數曲線可以發現，在加載初期，兩者均維持在較低的水平，到達C點后開始增加，增加幅度較穩定，一直到D點急劇增加.點C、D點對應的應力即為起裂應力和損傷應力.需要說明的是，試件在鉆取和加制樣過程中受到不同程度的擾動，導致其起裂應力不能通過聲發射進行較精準的識別，這里結合兩個特征參數進行綜合分析，必要時考慮分析其他更多特征參數，以減少識別誤差.

圖9 巖樣3-D2應力、AE事件率-時間關系曲線

Fig.9 Relation curves of stress and AE event rates of sample 3-D2 with time

2.2 BPM模擬法結果

以加載速率為5×10-5m/s時數值試件為例.試件在單軸壓縮過程中微裂紋的數量增長情況如圖10所示.可以看出，隨著應變增加，微裂紋開始出現并穩定增加，曲線的突變點對應的應力為起裂應力(圖10中E點)，此時裂紋數為2條，應力值為23.96 MPa，微裂紋數經過一段較平穩增加后，進入線性增長階段，此時的突變點對應的應力為損傷應力(圖10中F點)，值為45.68 MPa.同樣，采用此方法可以獲得不同加載速率下試件的特征應力值.

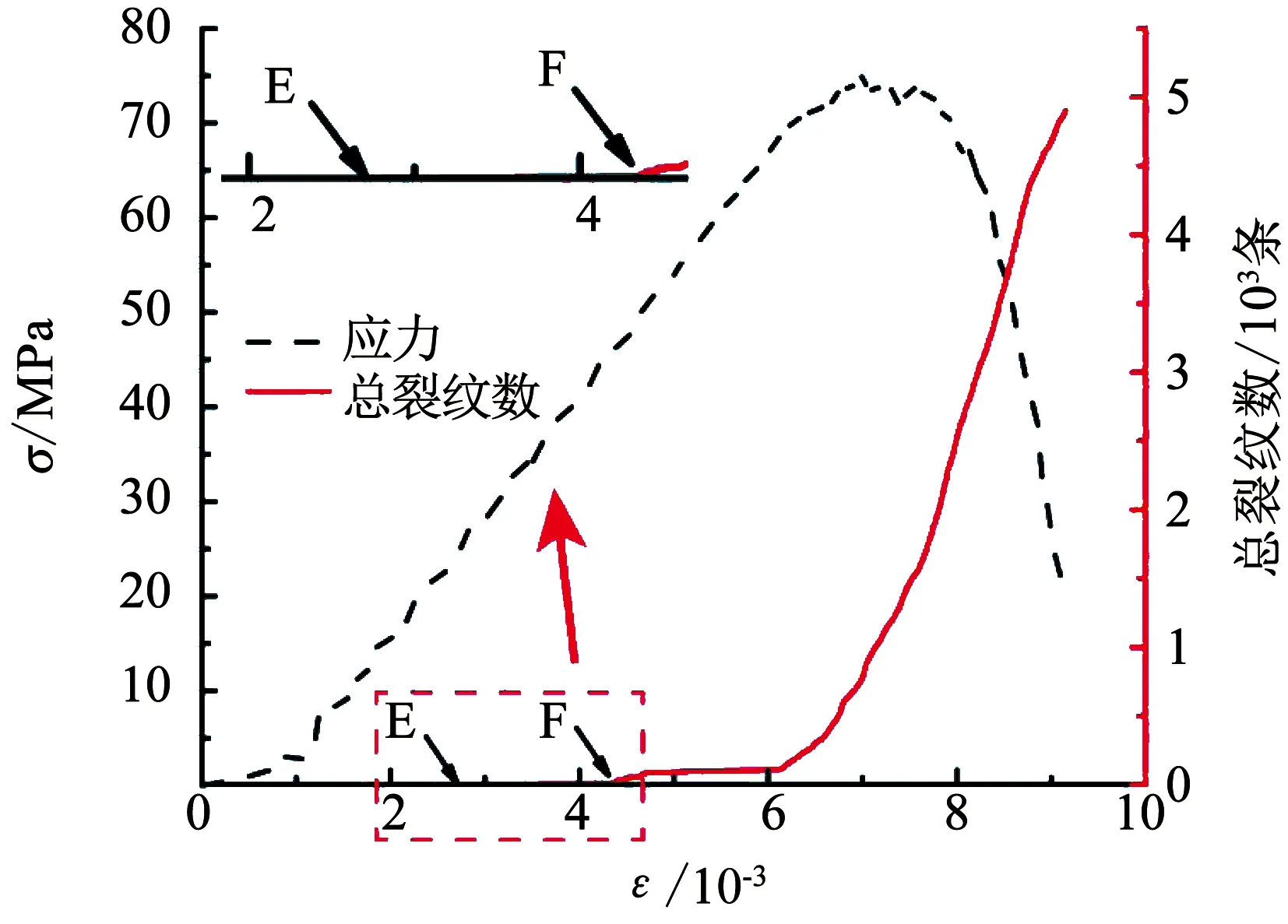
圖10 PFC2D數值模擬微裂紋數量變化和局部放大圖

Fig.10 Variation of micro-crack numbers simulated by PFC2Dand local magnification image

2.3 對比分析

由以上試驗法(體積應變法、聲發射法)和數值模擬法確定的大理巖特征應力歸一化結果如表3和圖11所示.其中σc′為PFC2D數值模擬獲得的峰值應力.結合表3、圖11可以看出，采用試驗體積應變法、聲發射法和BPM模擬法確定的不同加載速率下大理巖歸一化起裂應力范圍在0.30～0.41，歸一化損傷應力范圍在0.58～0.80.同一加載速率下各巖樣特征應力歸一化結果離散性較小，說明試驗用巖樣較均致，個體差異性較小.

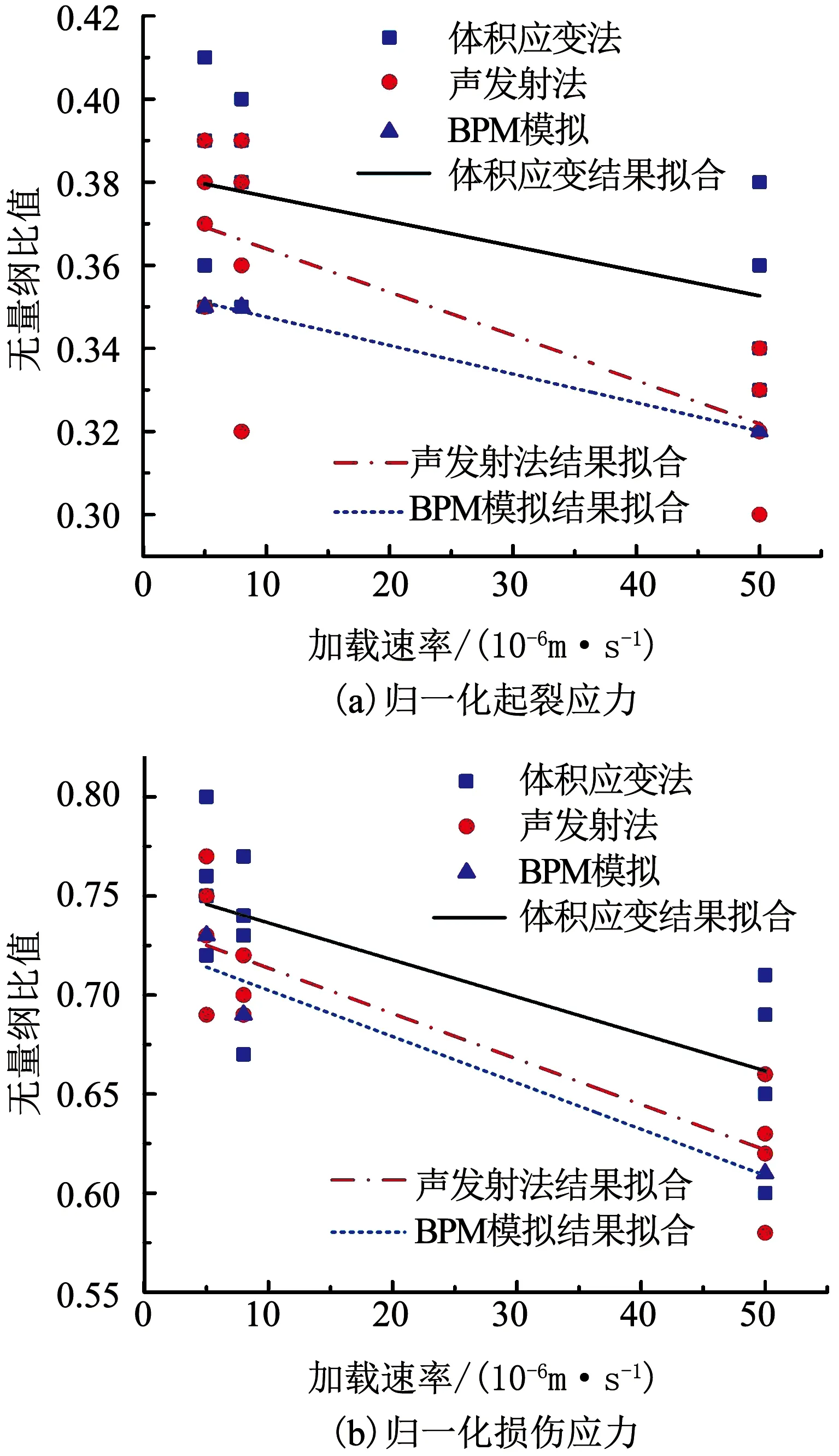
圖11 采用不同方法確定的巖樣歸一化特征應力

Fig.11 Normalized characteristic stresses of rock samples determined by different methods

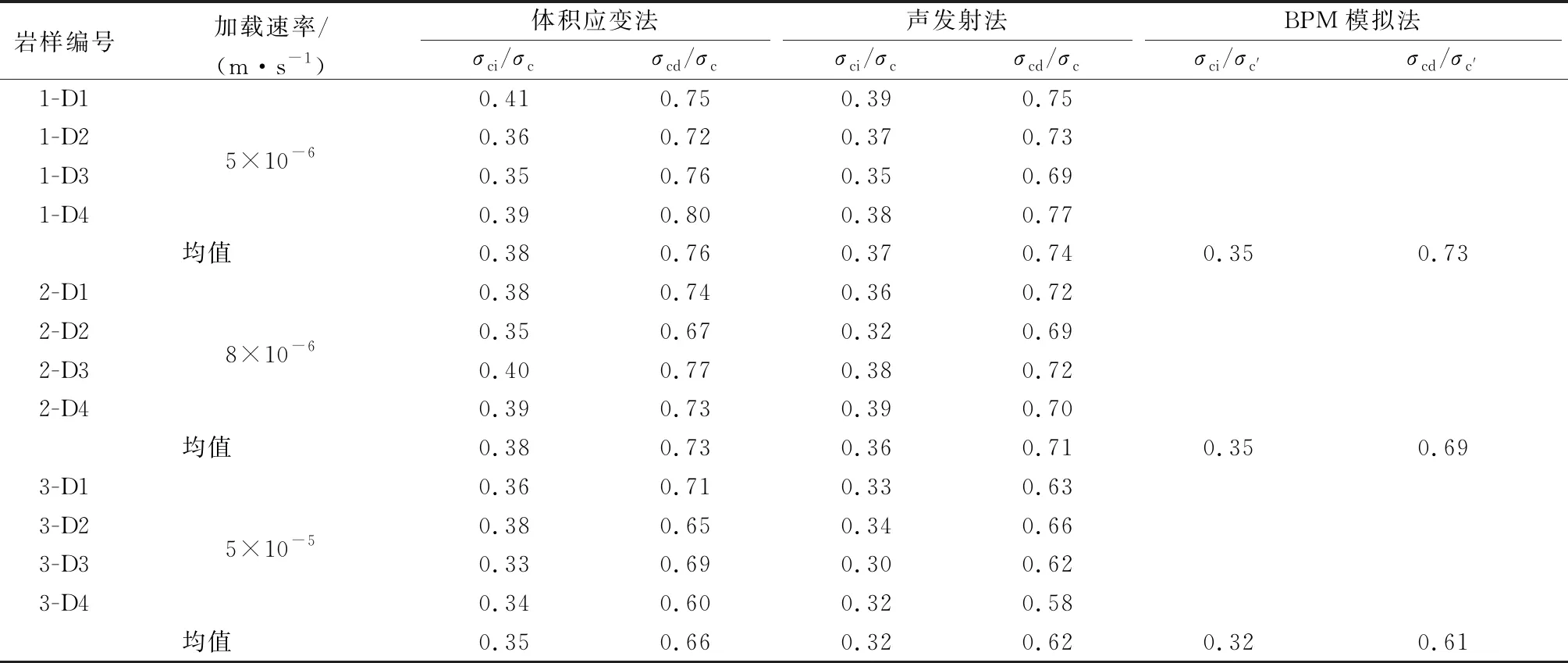
表3 不同加載速率下大理巖歸一化特征應力

當加載速率為5×10-6m/s，采用體積應變法、聲發射法確定的歸一化起裂應力均值與BPM模擬法確定的結果差值分別為0.03，0.02，歸一化損傷應力差值分別為0.03，0.01；當加載速率為8×10-6m/s，歸一化起裂應力差值分別為0.03，0.01，歸一化損傷應力差值分別為0.04，0.02；當加載速率為5×10-5m/s，歸一化起裂應力差值分別為0.03，0，歸一化損傷應力差值分別為0.05，0.01.發現不同加載速率下，BPM模擬法確定的特征應力值與體積應變法、聲發射法確定結果很接近，尤其與聲發射法結果相差無幾，且均小于后兩種方法確定值.普遍認為，由于材料宏觀響應滯后于細觀變化，BPM模擬法、聲發射法確定的特征應力一般小于宏觀體積應變法.以上說明基于微裂紋數量變化確定大理巖特征應力是一種較可靠有效的方法，其確定的特征應力較宏觀體積應變法偏小，但結果較為吻合.

加載速率由8×10-6m/s增加至5×10-5m/s時，3種方法確定的歸一化特征應力值均呈現減小規律.反映巖石在高加載速率條件下更容易形成內部損傷，微裂紋將在相對較低的應力時出現穩定和非穩定性擴展.

3 加載速率效應數值分析

為全面分析大理巖特征應力的加載速率效應，包括同一數量級不同加載速率和不同數量級加載速率，在試驗用3種加載速率基礎上，增加3種加載速率進行單軸壓縮數值模擬，加載速率分別為8×10-5，5×10-4，8×10-4m/s.數值模型與前文1.3節組建的模型一致.不同加載速率下PFC2D模擬得到試件的歸一化特征應力規律曲線如圖12所示.可以看出，在加載速率為5×10-6～8×10-4m/s內，隨著加載速率增大，各試件的歸一化起裂應力和損傷應力減小.這主要是因為在較快速率加載下，巖石內部幾乎來不及發生應力松弛，較小的裂紋等缺陷處于激活狀態，更容易滿足起裂條件，進而發生擴展和貫通，導致其歸一化起裂應力和損傷應力隨加載速率增大而減小.

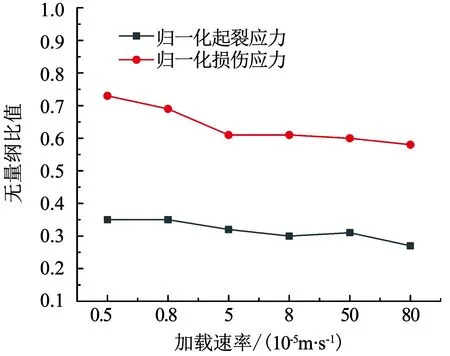
圖12 不同加載速率下PFC2D數值試件歸一化特征應力

Fig.12 Normalized characteristic stresses of PFC2Dnumerical specimens at different loading rates

當加載速率小于5×10-5m/s，即中低加載速率時，其歸一化特征應力降幅較大.當加載速率大于5×10-5m/s，即較高加載速率時，歸一化特征應力值整體上趨于平穩，尤其是歸一化損傷應力.巖石的變形破壞受多種因素影響，其中包括載荷速率.當加載速率較低時，巖石有流變趨勢；在中低加載速率條件下，表現為巖石變形的時效特征；當加載速率較高時，巖石出現延遲破壞特性.模擬結果顯示，在高加載速率時，損傷應力下降幅度較中低加載速率時小.說明對試驗用較均致的脆性大理巖而言，由于受到延遲破壞特性影響，沒有在預想的較低的應力水平發生微裂紋非穩定性擴展.值得注意的是，在加載速率為5×10-4m/s時，歸一化起裂應力出現增長，說明巖石的延遲破壞特性和前文提到的高加載速率下容易起裂的特性存在主次關系，且加載速率影響兩個歸一化特征應力值的規律似乎不完全相同.這也是后面可以深入研究的內容.

相比較而言，歸一化損傷應力的加載速率效應整體上比歸一化起裂應力明顯.

4 結 論

1)體積應變法、聲發射法、BPM模擬法3種方法確定的特征應力值較為接近，基于微裂紋數量變化的BPM模擬法確定大理巖特征應力是一種較可靠有效的方法.

2)試驗結果顯示，加載速率由8×10-6m/s增加至5×10-5m/s時，3種方法確定的歸一化特征應力值均呈現減小規律.

3)數值結果顯示，加載速率由5×10-6m/s增加至8×10-4m/s時，歸一化起裂應力和損傷應力減小.當處于中低加載速率時，其歸一化特征應力降幅較大.當處于較高加載速率時，歸一化特征應力值趨于平穩，尤其是歸一化損傷應力.相比較而言，歸一化損傷應力的加載速率效應整體上比歸一化起裂應力明顯.