單軸循環沖擊下花崗巖力學特性與損傷演化機理

王志亮，楊 輝，田諾成

(1.合肥工業大學 土木與水利工程學院，合肥 230009； 2.合肥工業大學 資源與環境工程學院，合肥 230009)

巖石是由礦物或巖屑在地質作用下按一定規律所組合成的集合體.不同的巖石由于其成分、結構與構造不同，在力學特性上呈現出很大的差異性.目前，在一些工程實踐中巖體會受到多次沖擊荷載的擾動，如地下硐室的鉆爆開挖、隧道掌子面的爆破施工以及機械開挖擾動都會給巖體施加循環動載.在循環沖擊荷載下巖石內部的微裂隙會不斷增多、擴展，進而相互貫通，形成宏觀裂紋[1].因此，研究巖石在循環沖擊荷載下的動態力學特性對于工程實踐具有重要意義.

目前，針對巖石類材料在循環荷載下的動態力學性能問題，許多學者已經開展了相應的研究工作.林大能等[2]利用壓力試驗機對大理石進行了循環沖擊試驗，發現相同荷載沖量下圍壓的存在可以提高試樣的沖擊強度，并降低其損傷演化的速率；金解放等[3]基于自行研制的SHPB裝置，研究了巖石在循環沖擊過程中典型的動態應力-應變曲線及反射波和透射波規律，并將應力-應變曲線分為5個階段；朱晶晶等[4]對花崗巖進行了單軸循環沖擊試驗，發現花崗巖的力學特性隨著沖擊次數的增加而逐漸劣化，且巖石的累積比能量吸收值在破壞前緩慢增長，而在破壞瞬間急劇增長；唐禮忠等[5]對矽卡巖進行了軸壓和循環沖擊荷載共同作用下的試驗研究，發現巖石在不同軸壓下的應力-應變曲線存在回彈和不回彈兩種特性；許金余等[6]研究了循環沖擊荷載下圍壓對斜長角閃巖動態力學特性的影響，指出相同圍壓下，巖樣的能量吸收率隨著應變率的提高而增大；宮鳳強等[7]研究了砂巖在三維靜載和循環沖擊荷載共同作用下的動態力學特性，發現圍壓不變，軸壓比在0.52～0.87變化時，砂巖的抗壓強度會隨著軸壓的增大而減小；Wang等[8]研究了不同溫度熱處理花崗巖在循環沖擊下的損傷演化規律，發現200 ℃后巖樣對循環沖擊荷載的抵抗能力最強，600 ℃后巖樣的抵抗能力最差，400～600 ℃存在一個花崗巖的溫度閾值；金解放等[9]對Logistic函數進行了逆變換，并建立了巖石在靜荷載與循環沖擊荷載共同作用下的損傷累積演化模型；Wang等[10]進行了鋼纖維混凝土的循環沖擊試驗，發現添加少量的鋼纖維可以顯著提高混凝土的抗沖擊性能，且相對于普通混凝土其破壞時裂縫尺寸較小.

與靜態循環載荷下巖石力學特性的研究成果相比，動態循環荷載作用下巖石的力學特性還處于起始階段，且其理論研究明顯落后于工程實際應用.基于此，本文擬利用改進的SHPB裝置，對黑云母花崗巖進行了單軸循環沖擊壓縮試驗，重點探究花崗巖的動態力學特性和損傷演化機理，并發展出巖石在循環沖擊荷載下裂紋起裂應力一種近似確定方法，從而嘗試對此類巖石在循環沖擊試驗中表現的現象進行合理的解釋.

1 試 驗

1.1 試樣制備

試驗材料取自陜西華山地區的黑云母花崗巖，其主要礦物成分有微斜長石Mc (41%)、斜長石Pl (27%)、石英Qz (22%)與黑云母Bt (7%)等，偏光顯微觀察如圖1(a)所示.為減小離散性和各向異性對巖石力學性質的影響，所有試樣均采用水鉆法從同一塊新鮮完整的大塊巖樣上沿同一方向鉆孔取得.根據國際巖石力學學會(ISRM)的建議[11]，將試樣加工成φ50×25 mm的圓柱體，加工后的黑云母花崗巖試樣如圖1(b)所示.試樣經打磨后，其端面不平行度控制在0.05 mm以內.

圖1 花崗巖組分及試樣

1.2 試驗原理

目前，巖石動力學測試設備常見的有高壓動三軸儀、分離式霍普金森壓桿(SHPB)和輕氣炮等[12].本次試驗采用華北理工大學改進的SHPB裝置，如圖2所示.該測試系統主要由氣腔室、紡錘形沖頭、入射桿、透射桿、緩沖桿、數據采集系統和分析系統等組成.彈性桿和沖頭由高強度合精鋼制成，密度為7 795 kg/m3，波速為5 797 m/s.入射桿與透射桿的長度均為2 m.該裝置最顯著的特點是沖頭為紡錘型，其撞擊入射桿后產生的半正弦波形有效增加了入射波的上升沿時且消除了波形的彌散效應，這有利于沖擊過程中彈性桿的一維應力傳播及試樣兩端達到應力平衡[13].

圖2 改進的霍普金森壓桿示意

在高壓氣體作用下沖頭以一定的速度沖擊入射桿，在入射桿中產生入射應力波，該應力波傳遞到試件端面時一部分通過試樣進入透射桿，另一部分反射回入射桿，通過貼在前后桿上的應變片可以測出入射波、反射波以及透射波的信號.采用適用于脆性材料數據處理的“三波法”[14]對采集到的應變信號進行處理，即可得到特定應變率下試樣應力-應變關系：

(1)

(2)

(3)

式中：Ae、As分別表示彈性桿和試樣的橫截面積；Ee表示彈性桿的彈性模量；Ce和Ls分別表示彈性桿的縱波波速和試樣的長度；εI(t)、εR(t)、εT(t)分別表示入射、反射以及透射波應變信號.

若試樣中應力均勻化、無衰減，引入輸入桿和輸出桿中的應變關系εI(t)+εR(t)=εT(t)，則上式可通過“二波法”[15]表示如下：

(4)

(5)

(6)

1.3 試驗方案

為了達到循環沖擊的目的，試驗開始前需要對試樣進行試沖以確定合適的沖擊荷載，從而防止試樣被一次沖壞.試沖時先固定子彈在發射腔中的位置不變，然后調整氣壓值對試樣進行試沖.最終確定的入射波應力幅值分別為110，90，70和50 MPa.每一種沖擊速度選取3～5個試樣，以保證至少能得到3個有效數據.試驗時，將黃油均勻地涂抹在試樣兩端以減小巖樣和彈性桿的摩擦，從而降低端部效應的影響.

與單次沖擊相同，循環沖擊試驗過程中試樣也需要滿足應力均勻性假設[16].圖3為C1試樣在第4次沖擊過程中的應力均衡圖，可以看出，入射波與反射波之和與透射波曲線在峰值應力之前基本重合，說明試樣中的應力已達到均衡狀態.

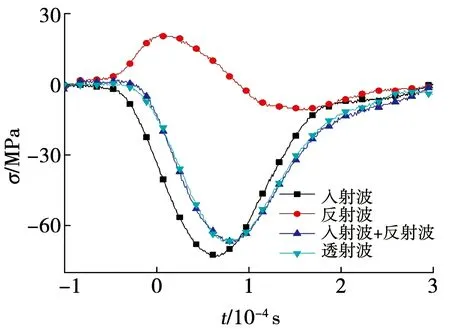
圖3 動態應力均衡圖

2 試驗結果分析

表1為部分試樣的力學參數和試驗結果，其中D1、D2和D3試樣在沖擊了20次之后均未發生宏觀破壞.限于篇幅，僅選擇代表性試樣進行分析.所謂代表性試樣為相同彈速下距平均循環沖擊次數最為相近的試樣.據此，僅對A1、B1、C1、D1試樣進行分析.

表1 花崗巖試樣的力學參數和試驗結果

2.1 原始波形圖分析

圖4為A1和D1試樣的循環沖擊原始波形.可以看出，每次沖擊波的入射波幅值基本一致，達到等幅循環沖擊的要求；隨著沖擊次數的增加，A1試樣的反射波峰值逐漸增大，而透射波峰值逐漸減小.根據式(5)可知，反射波越大其對應的應變率就越大；根據式(6)可知，透射波越小其對應的試樣應力就越小.故A1試樣的平均應變率隨著沖擊次數的增加而不斷增大，而峰值應力則在不斷降低，反映出試樣的損傷在逐漸增大.與A1試樣原始波形圖形成鮮明對比的是，D1試樣的反射波峰值和透射波峰值在經歷20次循環沖擊之后，并未發生明顯的變化.

圖4 循環沖擊原始波形

2.2 應力-應變曲線

圖5為試樣在不同循環沖擊荷載下的應力-應變曲線.定義加載段的最大應力為峰值應力，應變所達到的最大值為最大應變.由圖5可知，當試樣未破壞時，在峰值應力之前，應力-應變曲線的變化趨勢較為相似，大致可以分為兩個階段，起初都是一個近似的直線段，之后曲線進入非線性變形階段，曲線的斜率逐漸減小.峰值應力后，應力-應變曲線都有一定程度的回彈，試樣沒有表現出宏觀破壞，故卸載段會釋放所儲存的部分彈性能.

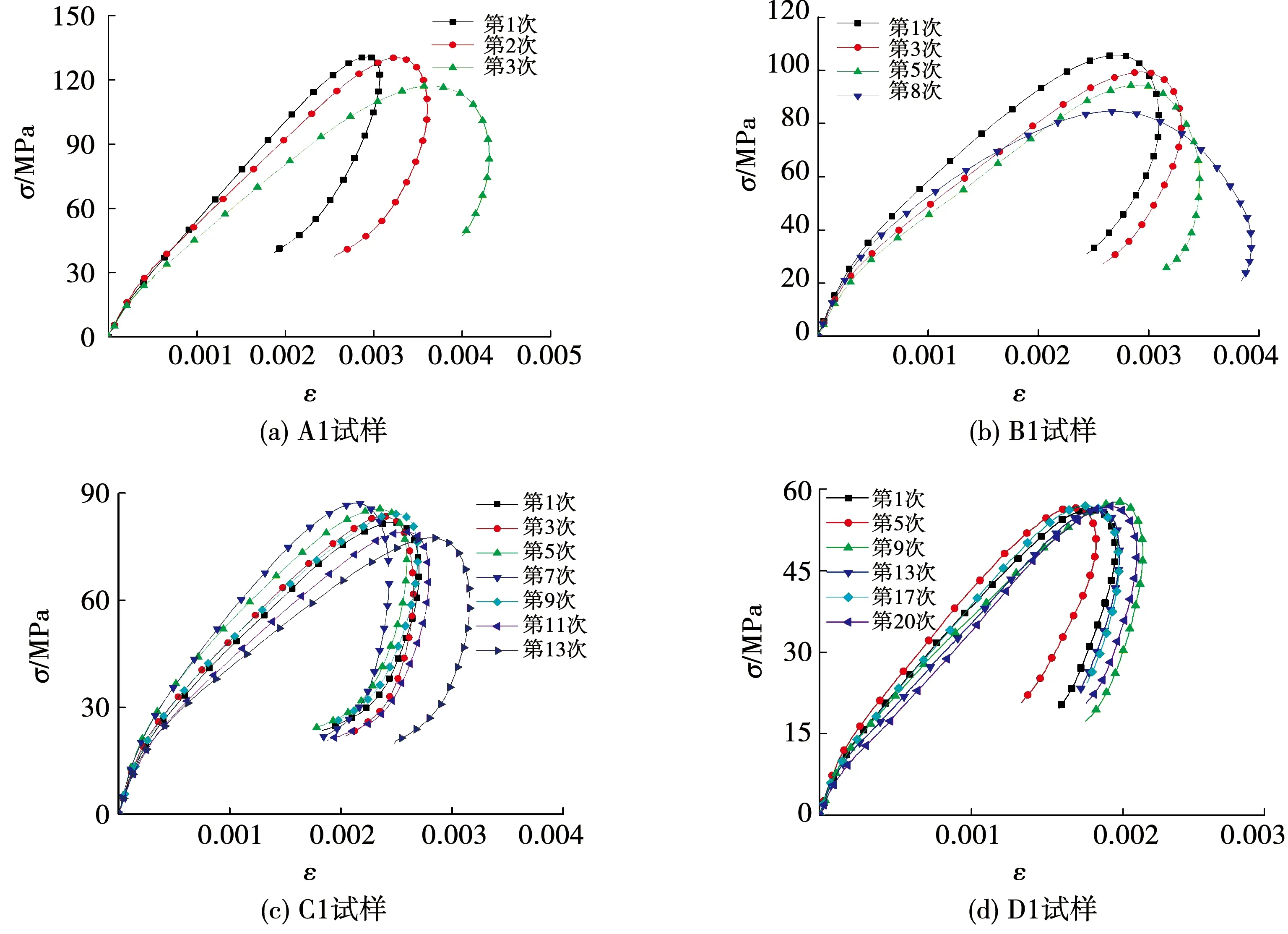
圖5 循環沖擊荷載下的應力-應變曲線

2.3 峰值應力與循環沖擊次數的關系

峰值應力隨循環沖擊次數的變化如圖6所示.可以看出，入射波應力幅值為110.57和90.48 MPa時，A1和B1試樣的峰值應力均隨著沖擊次數的增加而持續減小，表現為承載能力的持續劣化.根據一維應力波理論[12]，應力波在兩種不同的介質中發生反射與透射時，存在以下關系：

(7)

σR(t)=FσI(t),

(8)

(9)

σT(t)=(1+F)(1-F)σI(t).

(10)

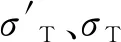
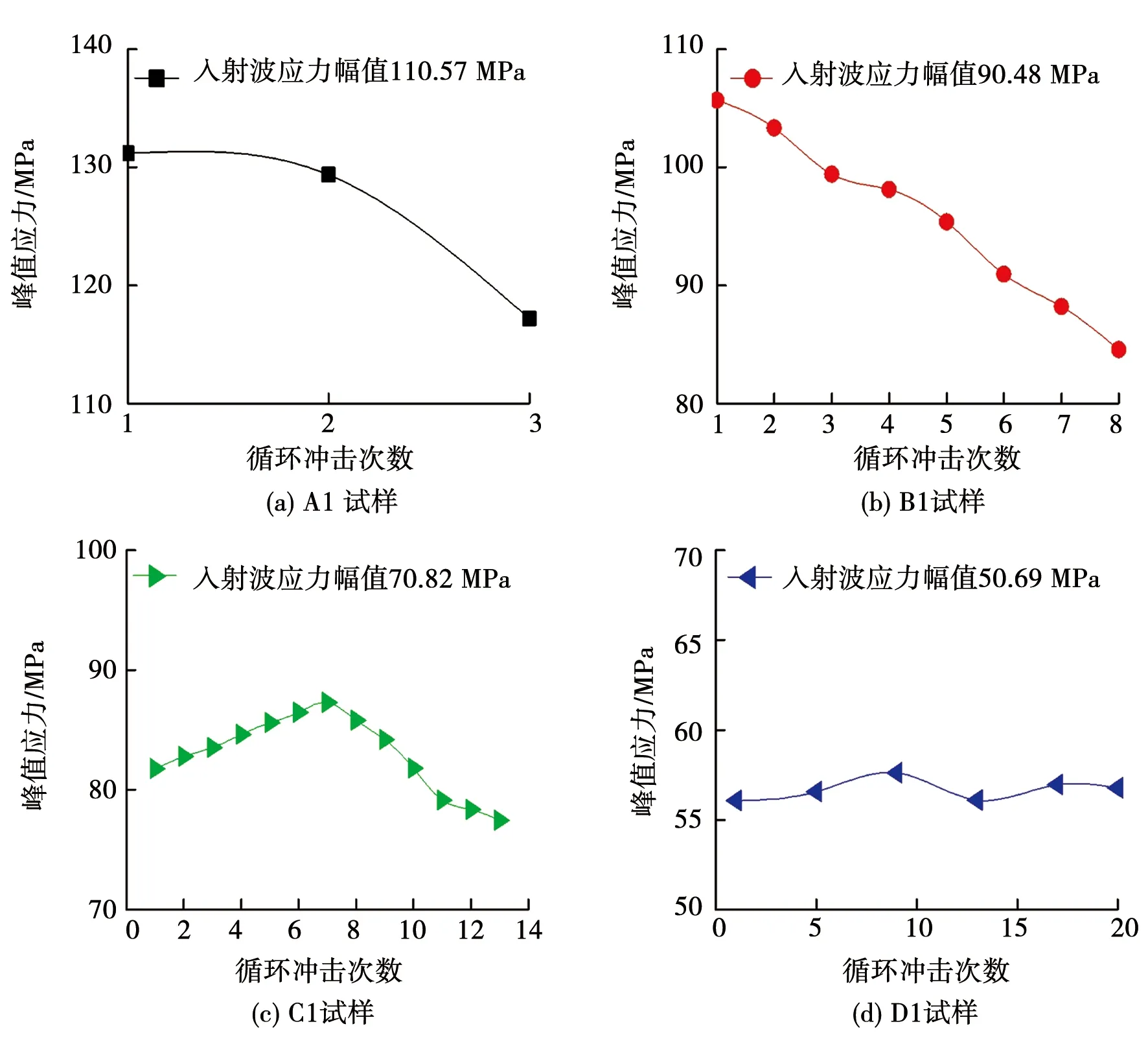
圖6 峰值應力與沖擊次數的關系

隨著循環次數的增加，巖石內部的損傷不斷增加，試樣的波阻抗不斷減小，導致反射系數F不斷減小，其絕對值不斷增加.由式(10)可知，若不考慮應力波在試樣內的多次透反射，當入射波保持恒定時，透射波不斷減小.因此，試樣A1和B1的峰值應力隨著沖擊次數的增加而不斷減小.入射波應力幅值為70.82 MPa時，在第7次沖擊之前C1試樣的峰值應力逐漸增大，之后其峰值應力又逐漸降低.分析認為，前7次沖擊所產生的損傷總體上小于試樣內微裂紋的閉合量[17]，壓密作用占據主導地位，所以，巖石的波阻抗逐漸增大，進而使得透射波越來越大，故前7次的峰值應力是不斷增大的.隨后，沖擊損傷軟化作用使得巖石內部損傷不斷累積，巖石的波阻抗不斷減小，峰值應力逐漸降低.與前3個試樣不同的是，D1試樣的峰值應力在經歷20次循環沖擊之后，并沒有發生明顯下降，其峰值應力在56 MPa上下浮動，間接地說明了巖石的波阻抗基本沒有變化，內部損傷不甚明顯.

2.4 最大應變與平均應變率的變化規律

試樣在沖擊過程中最大應變和平均應變率的變化規律如圖7，8所示.可以看出，最大應變和平均應變率隨沖擊次數的變化規律較相似，原因是它們都代表著巖石的變形能力.其中A1和B1試樣的最大應變和平均應變率隨著沖擊次數的增加而逐漸增大，這是因為巖石波阻抗的降低導致反射系數F的絕對值增大，通過式(8)可知反射波在逐漸增大，相應的應變率也就越大；巖樣的變形能力不斷減弱，故最大應變和平均應變率隨著沖擊次數的增加而不斷增大.C1試樣的最大應變和平均應變率則呈現出先減小后增大的趨勢，這是由壓密作用導致的巖石波阻抗先增大后降低引起的.而D1試樣的波阻抗基本沒有變化，所以，在相同的沖擊荷載下其最大應變和平均應變率沒有明顯的變化.

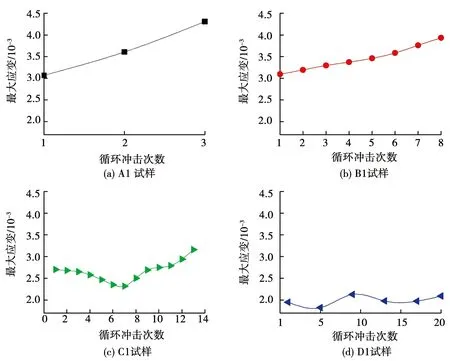
圖7 最大應變與沖擊次數的關系

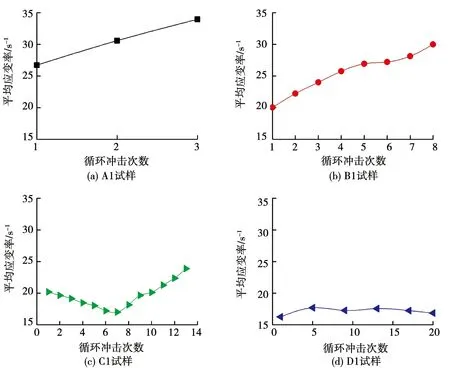
圖8 平均應變率與沖擊次數的關系

2.5 花崗巖損傷演化規律

為了探究循環沖擊下花崗巖的損傷演化規律，通過下式來定義損傷[8,18]：

(11)

式中En為第n次沖擊后巖石的彈性模量.

從巖樣沖擊載荷下的應力-應變曲線可以看出，壓密段并不明顯，峰前表現出較好的彈性變形，故本文彈性模量采用下式計算：

(12)

式中：σ表示軸向應力，ε為軸向應變，下標1和2分別對應應力-應變曲線峰值40%和60%的兩個點.

圖9為試樣在循環沖擊過程中損傷度D隨沖擊次數的變化，可以看出，不同沖擊荷載下花崗巖表現出不同的損傷演化規律.A1試樣的損傷近似呈線性增長，而且損傷累積速度大于其他3種情況；B1試樣的損傷則先增長較快然后趨于穩定；對于C1試樣，由于壓密作用使得前7次的沖擊產生了負損傷，第7次沖擊過后其損傷值達-0.25；之后內部裂隙加速擴展、貫通，所以，其損傷累積速度加快并且迅速上升為正值，最后破壞時其損傷值為0.22；D1試樣在經歷了20次沖擊后其損傷值只有0.05，而且其損傷值一直在較小的范圍內波動，并沒有出現增長的趨勢，所以,產生的損傷可以忽略不計.

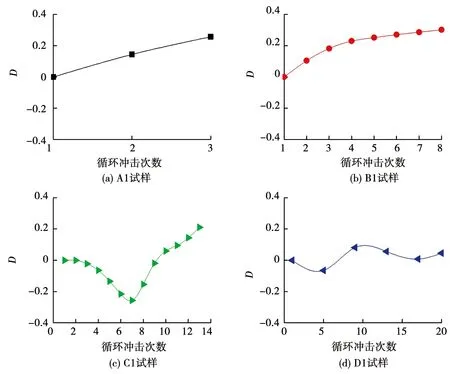
圖9 試樣損傷與沖擊次數的關系

2.6 循環沖擊下巖石損傷應力閾值

由圖6可知，與單次沖擊下峰值應力隨入射波應力幅值的增加而增加相同，循環沖擊荷載下試樣首次沖擊時的峰值應力亦隨著入射波應力幅值的增加而增加，即加載率效應.當入射波應力幅值分別為50.69，70.82，90.48和110.57 MPa時，試樣首次沖擊時的峰值應力分別為56，81.8，105.7和131.2 MPa.在進行巖樣疲勞試驗時，葛修潤等[19]發現周期疲勞荷載下巖樣存在一個疲勞破壞門檻值，該值細觀上對應巖石試件開始發生裂紋萌生的應力狀態；盧高明等[20]也指出當巖石試樣受到的上限應力大于該疲勞破壞門檻值時，巖石內部損傷不斷累積，且疲勞壽命隨著上限應力的增加不斷減小；當試樣受到的上限應力小于該疲勞門檻值時，巖石內部未有明顯損傷產生.從前面分析可看出，試樣首次沖擊時的峰值應力越大，力學性能劣化越快，試樣的損傷累積速度越快；當試樣首次沖擊時的峰值應力為56 MPa時，巖石內部沒有明顯損傷產生.因此，可以認為在SHPB循環沖擊荷載下，同樣存在一個裂紋起裂應力值.

Brace等[21]和Bieniawski[22]發現了低孔隙度巖石無側限和受限試驗的應力-應變曲線中有4個關鍵點，分別是軸向應變中的裂紋閉合點、側向應變中的裂紋起裂點、體積應變中的非穩定裂紋增長點以及軸向應變的峰值點.Nicksiar等和Martin[23-24]在對巖石做了大量靜態壓縮試驗后，發現利用巖石靜態壓縮應力-應變曲線可以得出其裂紋起裂應力值、非穩定裂紋增長應力值和峰值應力值，又叫“側向應變響應法”，其主要步驟如下：(i)通過體應變曲線的反彎拐點，確定出裂紋非穩定增長的起始應力值；(ii)在軸向應力和側向應變曲線上，連接側向應變0點和裂紋非穩定增長的起始應力點，可得側向應變的參考線；(iii)計算出側向應變曲線和參考線之間的差值，用ΔLSR表示；(iv)繪制軸向應力和ΔLSR之間的曲線，并利用拋物線方程進行最佳擬合；(v)依據所得到拋物線上側向應變差的最大值，確定出靜態裂紋起裂應力值.

本文所研究的華山花崗巖試樣的靜態壓縮應力-應變曲線如圖10所示.采用上述方法，從圖10的軸向應力-體積應變曲線上判讀出體積應變的最大點作為此巖石的非穩定裂紋增長點，對應的應力值為96.4 MPa，而軸向應力-軸向應變曲線的峰值應力等于144.8 MPa.圖11給出了利用側向應變響應法確立裂紋起裂應力過程，可見此花崗巖的靜態裂紋起裂應力值約為60.1 MPa.據此可知靜態裂紋起裂應力與靜態壓縮強度的比值為0.415.

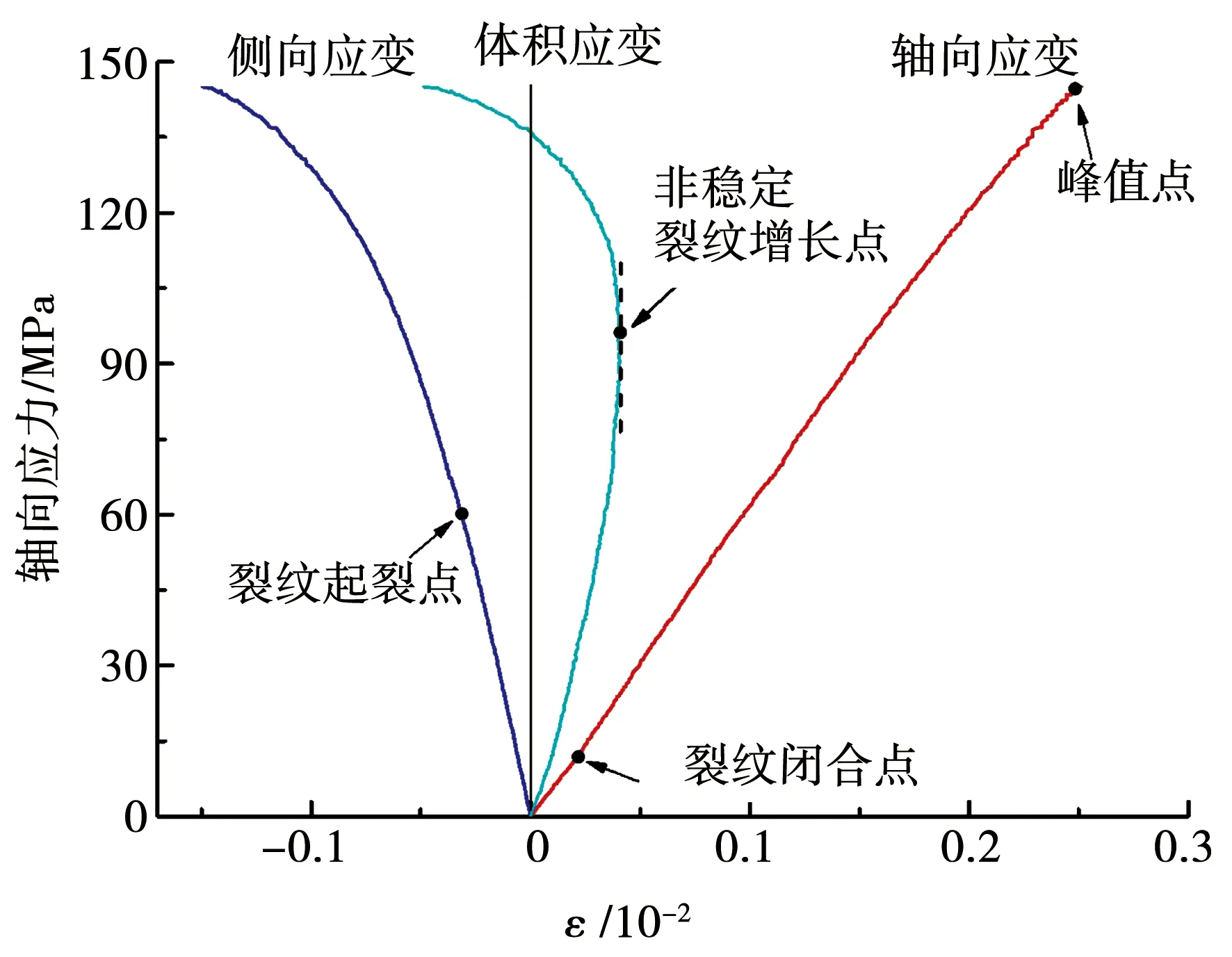
圖10 花崗巖靜態壓縮應力-應變曲線

梁昌玉等[25]的研究表明，巖石的裂紋起裂應力和峰值強度均隨著應變率的增加而增加，但巖樣的起裂應力和峰值強度的比值與應變率無明顯的相關性.由此，近似提出動態起裂應力的計算式如下：

(13)

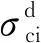
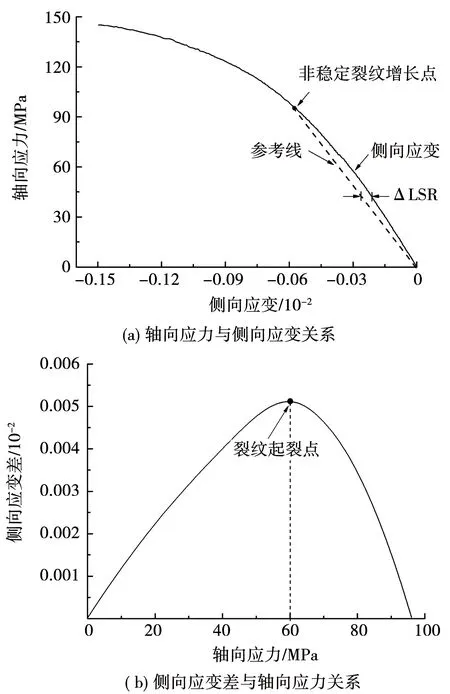
圖11 利用側向應變響應確立裂紋起裂應力

Fig.11 Evaluation of crack initiation stress using lateral strain response

3 結 論

1)入射波應力幅值為110.57和90.48 MPa時，隨著沖擊次數的增加，其峰值應力逐漸降低，最大應變與平均應變率則相反；入射波應力幅值為70.82 MPa時，初始幾次沖擊會使巖樣中部分裂紋閉合，整體處于壓密階段；當入射波應力幅值降為50.69 MPa時，巖樣的力學性質基本沒有明顯變化.

2)不同循環沖擊荷載下試樣呈現不同的損傷演化規律，入射波應力幅值為110.57和90.48 MPa時，損傷累積速度較快；入射波應力幅值為70.82 MPa時，損傷值先降為負值之后又快速增長為正值；而入射波應力幅值為50.69 MPa時，試樣內部產生的損傷較小，可忽略不計.

3)由于SHPB沖擊壓縮試驗中難以準確獲取試樣的側向應變信號，本文把基于靜態壓縮應力-應變曲線推求到的裂紋起裂應力，乘以一個強度放大比例系數，從而發展出特定應變率下的巖樣動態裂紋起裂應力的近似確定方法，結果能較好地解釋循環沖擊試驗中觀測到的現象.