傳統組合導航中的實用Kalman濾波技術評述
嚴恭敏,鄧 瑀
(西北工業大學自動化學院,西安 710072)
0 引言
估計理論是概率論與數理統計的一個分支,它是根據受擾動的觀測數據來提取系統某些參數或狀態的一種數學方法。1795年,高斯提出了最小二乘法;1912年,費歇爾(R.A.Fisher)提出了極大似然估計法,從概率密度的角度考慮估計問題;1940年,維納提出了在頻域中設計統計最優濾波器的方法,稱為維納濾波,但它只能處理平穩隨機過程問題且濾波器設計復雜,應用受到很大限制;1960年,卡爾曼基于狀態方程描述提出了一種最優遞推濾波方法,稱為Kalman濾波,它既適用于平穩隨機過程,也適用于非平穩過程,一經提出便得到了廣泛應用。在Kalman濾波器出現以后,針對隨機動態系統的估計理論的發展基本上都是以它的框架為基礎的一些擴展和改進[1]。
Kalman濾波器最早和最成功的應用實例便是在組合導航領域。慣性導航系統(Inertial Navigation System,INS)是最重要的一種導航方式,它能提供姿態、方位、速度和位置,甚至還包括加速度和角速率等導航信息,可用于運載體的正確操縱和控制。慣導具有自主性強、動態性能好、導航信息全面且輸出頻率高等優點,但其誤差隨時間不斷累積,長期精度不高。相比而言,全球導航衛星系統(Global Navigation Satellite System,GNSS)的優點是精度高且誤差不隨時間增大,缺點是導航信息不夠全面、信號容易受到干擾、在室內等環境下接收不到衛星信號而無法使用。慣導和衛導之間具有很強的互補性,慣導/衛導組合導航提高了系統整體的精度和可靠性,被公認為是最佳的組合導航方案[2]。除了慣導和衛導外,傳統的輔助導航方法有里程儀(或多普勒計程儀)、高度表和地磁方位(多用于低精度場合),當然還有天文導航、地圖/重力/地磁匹配導航等,但是后者不太常用或應用領域相對比較狹窄。隨著機器人和自動駕駛技術的興起,激光雷達、視覺圖像、即時定位與地圖構建(Simultaneous Localization and Mapping,SLAM)、因子圖(factor graph)和人工智能(Artificial Intelligence,AI)等導航手段或數據處理方法不斷涌現,組合導航和信息融合新技術的研究和發展方興未艾[3-6]。限于筆者的知識面,論文主要討論了傳統Kalman濾波組合導航算法,以慣導/衛導組合為例,指出實際Kalman濾波應用中可能遇到的問題及其解決思路,希望能為工程技術人員提供一些有實用價值的參考。
1 Kalman濾波基本原理
給定Kalman濾波隨機系統的狀態空間模型
(1)
式中,Xk是n維的狀態向量;Zk是m維的量測向量;Φk/k-1、Γk-1和Hk是已知的系統結構參數,分別稱為n階的狀態一步轉移矩陣、n×l階的系統噪聲分配矩陣、m×n階的量測矩陣;Wk-1是l維的系統噪聲(或稱過程噪聲)向量,Vk是m維的量測噪聲向量,兩者都是零均值的高斯白噪聲向量序列,且它們之間互不相關,即滿足
(2)
式中,δkj為克羅內克函數。式(2)是Kalman濾波狀態空間模型中對于噪聲要求的基本假設,一般要求Qk是非負定的且Rk是正定的,即有Qk≥0且Rk>0。實際上,通過選擇合適的噪聲分配陣Γk-1,可以保證Qk總是正定的[1]。
經過推導,標準(或稱傳統)Kalman濾波包含5個基本公式,分別為:
1)狀態一步預測
(3)
2)狀態一步預測均方誤差陣
(4)
3)濾波增益
(5)
4)狀態估計
(6)
5)狀態估計均方誤差陣
Pk=(I-KkHk)Pk/k-1
(7)
其中,式(3)和式(4)統稱為時間更新,式(5)~式(7)統稱為量測更新;式(3)和式(6)組成濾波計算回路(一階矩計算),式(4)、式(5)和式(7)組成增益計算回路(二階矩計算)。注意到濾波計算回路受增益計算回路的影響,而濾波計算回路不對增益計算回路產生任何影響。
對于可觀測性較強的狀態分量,對應的狀態初值和均方誤差陣設置偏差容許適當大些,它們隨著濾波更新將會快速收斂,如果均方誤差陣設置過小,則當初始狀態誤差較大時會使狀態收斂速度緩慢,變為有偏估計。而對于可觀測性較弱的狀態,對應的狀態初值和均方誤差陣應該設置得盡量準確,如果均方誤差陣設置過大,容易引起狀態估計過程中的有偏或劇烈波動;反之,如果均方誤差陣設置過小,同樣會使狀態收斂速度變慢,這兩種情況下均方誤差陣計算值都不宜用于評估相應狀態估計的精度。對于不可觀測的狀態分量,其狀態估計及其均方誤差陣不會隨濾波更新而變化,即不會有濾波效果。例如在不轉位的慣導Kalman濾波初始對準中,等效水平加速度計隨機常值零偏(等效東向陀螺隨機常值漂移)的方差設置太大會影響水平(方位)失準角的估計,因為兩者是相互依賴的且通常認為前者的可觀測性較弱,只有前者設置得適當的小,后者的估計精度才會比較高。
2 慣導/衛導組合導航系統建模
常用的Kalman濾波是離散形式的,但在實際系統分析和建模時,多是以連續時間形式表示。慣導/衛導組合導航Kalman濾波的連續時間隨機系統模型如下
(8)
(9)
其中
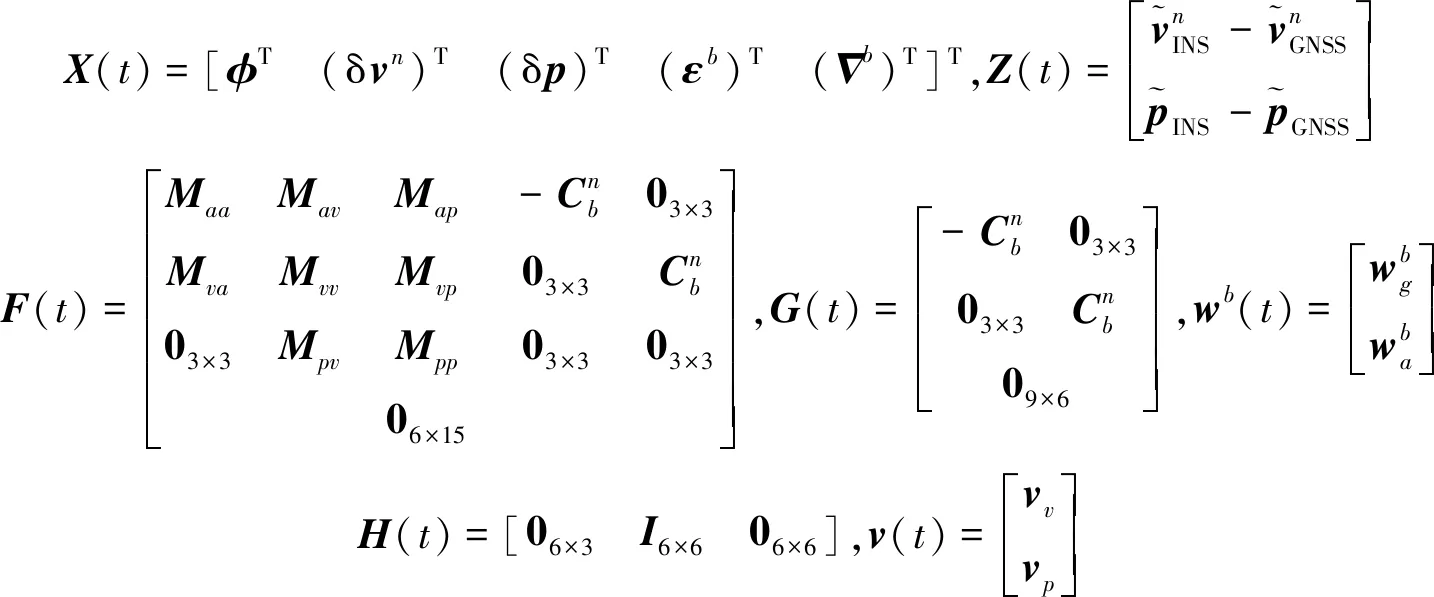
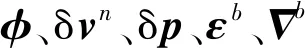
式(8)是一種比較常用的慣導/衛導組合15維狀態建模,主要考慮了慣性器件典型誤差和慣導導航參數解算誤差,且將衛導測量誤差視為簡單的白噪聲,它能夠滿足大部分的實際應用。對于海上或無需精密高度定位的場合,為了降低濾波器維數和計算量,有時可將天向通道中的加速度計隨機常值偏值、速度誤差和高度誤差簡化刪去。但是,對于捷聯慣導而言,如果導航運行過程中俯仰或橫滾角機動變化較大,此時載體坐標系中的3個加速度計隨機常值偏值容易從天向通道中辨識出來,高度通道不宜再作簡化處理。
對于慣導而言,組合導航的主要目的在于通過速度或位置量測估計出失準角甚至慣性器件誤差,提高慣導系統精度。在實際應用中,速度量測和位置量測之間是存在一定程度的信息冗余的。在高精度慣導中,失準角和慣性器件誤差都比較小且穩定,需要較長時間才能估計出這些誤差,通常有位置量測就可以,而不需要速度量測。在低精度慣導中,失準角和慣性器件誤差都相對較大且不穩定,需要通過速度量測才能更快速地估計出這些誤差,如果僅用位置量測則往往不能起到很好的誤差抑制效果,除非實際位置測量噪聲非常小。
不同導航系統之間進行測量參數或導航參數比對組合,往往都得考慮兩者之間的時空不同步差異問題,即桿臂誤差和時間不同步誤差。根據實際情況,考慮是否將這些誤差量增廣列作Kalman濾波狀態。
對于慣導與衛導之間的桿臂誤差,建議事先進行準確測定,再作為已知參數設定并補償,這樣有利于降低濾波器維數。除非在某些特定的高精度應用場合,如機載定位定向系統(Position and Orientation System,POS)中,衛導天線安裝在飛機蒙皮上方,慣導安裝在機腹儀器倉內,難以準確測量出兩者的相對位置,此時需將不能準確測定的桿臂誤差列為狀態。一般情況下,慣導精度等級越低或載體轉動機動性越差,將越難通過濾波方法估計出桿臂誤差,因而在低精度慣導中應當盡量事先給出準確的桿臂參數。
接下來分析時間不同步問題。通常導航計算機接收到慣性器件信號的延遲較少,而衛星信號從采集到定位解算再到傳輸給導航計算機,可能存在幾十甚至一、二百毫秒的延遲,有些衛導系統延遲時間還不固定,這對高速飛行器的組合導航系統而言是十分不利的。有些情況下,時間延遲波動帶來的誤差遠大于衛導本身的定位誤差,例如飛機速度200m/s,延遲150ms將會引起30m的時間不同步定位誤差,而衛導定位誤差一般小于10m。如果衛導相對于慣導時間延遲基本固定不變,則可以作為狀態進行濾波估計,在一定量級的載體加速度機動條件下是可觀測的。如果時間延遲參數存在波動又難以準確估計,則應當優先考慮在組合導航系統硬件設計上做好同步處理和補償,否則只能從軟件算法上等效放大衛導的量測噪聲(不好處理的非白噪聲),相當于降低了衛導的測量精度,必然會對組合導航系統造成負面影響。
顯然,慣導的系統級標定或初始精對準過程均可視為一種特殊的組合導航算法,它們都以靜止零速為參考速度,慣導解算速度即為速度誤差觀測量。系統級標定將慣性器件的漂移誤差、刻度系數誤差,以及器件之間的安裝誤差等待標定參數都擴充為濾波狀態,通過一套完整的轉動方案充分激勵出所有誤差源的影響,借助Kalman濾波器從導航速度誤差量測中估計出待標定參數。精對準的主要目標在于從導航速度誤差中估計出失準角,有時還能夠估計獲得部分慣性器件誤差或抵消慣性器件誤差的影響,例如多位置對準方法、單軸或雙軸旋轉對準方法等。
3 連續時間隨機系統的離散化問題
在導航計算機上運算的Kalman濾波總是離散化形式的,針對如式(8)給出的連續時間隨機系統,在使用Kalman濾波之前必須先進行離散化處理。隨機系統離散化與確定性系統離散化最大的區別在于對輸入噪聲的等效處理。
簡記Xk=X(tk)、Γk-1=G(tk-1)、Zk=Z(tk)和Hk=H(tk),且記Ts為離散化間隔,對式(8)等效離散化,可近似得式(1),其中
(10)
Qk-1≈q(tk-1)Ts
(11)
Rk≈r(tk)/Ts
(12)

在式(8)所示的量測模型中,v(t)為連續時間白噪聲,r(t)為其功率譜密度,理論上連續時間白噪聲的帶寬無限,只是一種理想化的建模表示,這在實際系統中是不可能存在的。在實際應用中,大多數系統的量測方程是以離散形式直接給出的,如果在一定量測頻率范圍內量測噪聲的方差大小基本不變,則在量測設備允許的條件下選用較高的量測頻率對提高濾波估計精度是有益的;如果系統狀態變化比較平緩,為了降低量測更新頻率和減少計算量,則可將相繼多次量測作平均處理,并相應減少量測噪聲,利用平均量測進行Kalman濾波量測更新與進行高頻率量測更新是基本等效的。例如在以速度為量測的擾動基座Kalman濾波初始對準中,反映失準角變化規律的慣導速度為緩變量,外界基座干擾為快變量,可利用一段時間內(如1s)的平均速度代替瞬時速度作為量測,這樣可在減少基座干擾影響的同時降低量測更新頻率。式(12)正說明了,在r(tk)為緩變或定值的情況下,若使用較長的量測離散化間隔Ts,則需要設置較小的噪聲參數Rk。
4 噪聲相關條件下的建模問題
在標準Kalman濾波中關于噪聲的基本假設滿足式(2),如果不滿足該條件,通常稱其為噪聲相關條件下的Kalman濾波,主要包括系統噪聲與量測噪聲相關、系統噪聲為有色噪聲、量測噪聲為有色噪聲三種情形[1-2]。
處理系統噪聲與量測噪聲相關的方法是將量測引入狀態方程,從而消除相關性。事實上,系統噪聲與量測噪聲相關的實際系統例子非常罕見,即使相關也很難準確獲得它們之間的相關性矩陣,因而該種情形往往只有理論上探討的意義。
對于系統噪聲或量測噪聲為有色噪聲的情形,通行的做法是對有色噪聲建模,將其表示為白噪聲激勵的輸出,即對有色噪聲進行白化處理,再將有色噪聲模型列入系統方程,構成增廣系統。由于Kalman濾波采用狀態方程描述系統,因而理論上只有能夠用有限維狀態方程描述的有色噪聲才能作增廣處理。實際應用時多將有色噪聲近似成AR(p)模型(p階自回歸時間序列模型),而且階次一般不會太高,往往取1階(至多2階)就足夠了[8]。
以慣導/衛導組合導航為例,常將陀螺漂移(加速度計零偏類似)建成如下誤差模型
ε=εb+εr+εw
(13)
式中,εb為隨機常值過程,εr為相關過程,εw為角速率白噪聲,三者分別表示陀螺漂移誤差中的不易變部分(隨機常值)、緩變部分和快變部分。如果將慣性器件中相關過程都建模成AR(1)模型,則6個慣性器件(3個軸陀螺+3個軸加速度計)將增加6維狀態,如果采用AR(2)模型則需增加12維狀態,這對Kalman濾波器而言增加了很大的計算負擔。從實用角度看,太復雜的慣性器件建模方法是不可取的,能大幅提高導航系統精度的結論也是不可信的[9-10]。在實際應用中,一般以“隨機常值+白噪聲”或“AR(1)相關過程+白噪聲”建模就足夠了,前者多用于器件誤差變化時間相對于系統工作時間而言比較長(相對穩定)的情形,而后者主要用于誤差變化時間相對較短的情形。
對于衛導量測噪聲,建模為AR(1)也足夠了,實際上衛導測量序列前后之間的相關性也很小,特別在量測間隔較大時(1s量級),完全可近似為白噪聲。同時,可將量測噪聲矩陣當作對角陣看待,進而使用序貫Kalman濾波進行計算,避免了矩陣求逆運算,濾波結果與非對角陣量測噪聲設置之間的差別不大。
另外指出,在導航中影響導航精度的主要因素是慣性器件的長時間相關誤差項,而短相關或白噪聲的貢獻一般非常小,導航算法本身就是個積分過程,具有較強的高頻噪聲抑制能力。因而在導航算法前端應用數字濾波、小波濾波甚至神經網絡濾波等手段進行去噪的做法是沒什么意義甚至不可取的,降噪作用不大,反而有可能引起系統帶寬變窄。前述所說的AR建模主要指的也是對相關時間較長項建模,而對于較短項完全可以忽略。
5 濾波快速計算問題
標準Kalman濾波算法的計算量(主要指浮點乘法運算次數)與狀態維數的三次方成正比,狀態維數的增加,使得計算量呈幾何級數增長,高維系統的濾波對于導航計算機來說是一個沉重的負擔,對于單片機之類的嵌入式系統而言尤其如是。
在運載體機動情況下,高精度的捷聯慣導系統要求較高的慣性器件采樣頻率和導航解算頻率。同理,在組合導航Kalman濾波中,為了獲得高精度的慣導誤差狀態及其均方誤差陣的傳播,也需要較高的Kalman濾波時間更新頻率。據分析,在組合導航Kalman濾波中狀態均方誤差陣預測的計算量最多(而非量測更新的矩陣求逆計算),約占70%以上。針對狀態轉移矩陣Φk/k-1為稀疏矩陣的特點,常規算法存在大量的乘零運算操作,白白浪費了計算量,文獻[11]提出了一種矩陣外積法,使得均方誤差陣預測Pk/k-1所需的乘法次數降為s2-u2(其中s和u分別為狀態轉移矩陣中非零元素的個數和數值為1的元素個數)。更進一步地,文獻[12]基于系統矩陣為稀疏矩陣、量測噪聲方差陣為對角陣且量測矩陣的非零元均為1,以及慣導水平通道和高度通道弱耦合的特點,提出了均方誤差陣預測直接展開計算,采用量測更新序貫濾波處理,以及將系統矩陣中次要元素強制置零和降維次優濾波等措施,極大地減少了Kalman濾波的乘法計算次數。直接展開計算法不僅減少了乘法計算量,還減少了用于程序循環控制的變量計算和比較次數,最終濾波運行速度與常規算法相比可提高1個數量級以上。當然,直接展開計算法的缺點是增加了程序的代碼長度,典型的慣導/衛導組合算法程序約增加50k字節左右。
特別地,在低精度微機電系統(Micro-Electro-Mechanical System,MEMS)慣導/衛導組合中,根據物理含義,可以明顯地知道某些系統狀態分量之間是幾乎無關的(例如陀螺隨機常值漂移與桿臂誤差之間)或弱相關的(例如失準角與位置誤差之間、陀螺隨機常值漂移與速度誤差之間),因而可以直接將它們之間的均方誤差陣相應元素置零,無需計算,以節約計算量并減少程序代碼。但需要注意的是,置零可能引起均方誤差陣的非正定,這需要與均方誤差陣下限設置技術結合使用,詳見第11節。
實際系統中,捷聯慣導算法的更新頻率通常在100Hz以上,組合導航Kalman濾波的時間更新頻率建議不低于10Hz。如果在一個慣導算法更新周期(10ms)內無法完成一次Kalman濾波時間更新,則可以將Kalman濾波時間更新分散成計算量大致相同的數小片(比如50小片),每10ms僅計算其中的一部分(10小片),這樣在5個慣導算法更新周期(50ms)內便可完成一次Kalman濾波時間更新,同理也可將量測更新作同樣的分散處理。這種分散處理的計算技術稱之為時間分散Kalman濾波(Time-Distributed Kalman Filtering,TDKF)算法[13]。
6 平方根濾波問題
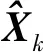
平方根濾波算法主要是針對均方誤差陣更新過程設計,采用均方誤差陣Pk的平方根進行循環更新,以減少數值表示的位數和減小計算誤差。與標準Kalman濾波算法相比,平方根濾波計算只需要大約一半的有效數字位數就能達到同樣的濾波精度,這在早期計算機位數不高時(單精度浮點甚至定點情形)是特別有效的。
下面以捷聯慣導的天向失準角誤差傳播方程為例來說明Kalman濾波所需的有效數字位數。天向失準角誤差方程為
(14)
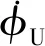
常用的平方根濾波算法有Potter平方根濾波、奇異值分解(Singular Value Decomposition,SVD)濾波、UD分解濾波和信息平方根濾波等算法[1-2]。如果導航計算機僅支持單精度浮點運算,則需要考慮采用平方根濾波算法,并優先推薦使用UD分解濾波算法,而其他平方根濾波算法必要性不大。目前大部分計算機都支持雙精度浮點運算,此時在組合導航Kalman濾波應用中則完全沒有必要再采用平方根濾波算法,因為平方根濾波算法的計算量總是大于常規濾波算法的。
另外指出,表示導航參數比表示導航誤差需要更多的有效數字位數。在慣導解算中,如果慣導速度的精度為0.001m/s,定位解算周期為T=0.01s,根據如下緯度更新公式可大致分析一下緯度表示所需的有效數字位數為
Lm=Lm-1+vN,m-1T/RMh
(15)
式中,不妨假設前一時刻的緯度取值Lm-1=1(rad),由vN,m-1T/RMh≈10-12(rad)可知,為了準確得到當前時刻的緯度Lm,其表示需要12位有效數字,才會使得在大數與小數相加過程中小數不會被完全湮沒。從以上計算分析過程看,適當延長導航更新周期T(即降低采樣頻率)可以在一定程度上減小數字表示位數,這對平臺慣導系統而言是合適的,但對同時存在角運動和線運動的高動態捷聯慣導系統來說是不可行的,因為在捷聯慣導解算中為補償不可交換誤差,動態越大采樣率要求就越高。
綜上所述,無論從慣導解算還是從組合濾波角度看,除非作特殊處理,應當在硬件上選用具備雙精度浮點運算能力的導航計算機。
7 自適應濾波與強跟蹤濾波問題
理論上,只有在隨機動態系統的結構參數和噪聲統計特性參數都準確已知的條件下,標準Kalman濾波才能獲得狀態的最優估計。然而,實際應用中以上兩類參數的獲取都或多或少存在一些誤差,致使Kalman濾波的精度降低,嚴重時還可能會引起濾波發散。不難理解,隨機系統的模型誤差往往會影響到其輸出,換言之,量測輸出中很可能隱含了關于系統模型(例如噪聲參數)的某些信息,那么當系統模型參數不夠準確時就有可能根據量測輸出對部分參數進行自適應估計建模,這實質上屬于系統辨識問題。
自適應濾波的方法很多,比較常見的一種狀態空間模型描述為
(16)
(17)
其中,qk、rk、Qk和Rk為待自適應辨識的噪聲參數。
文獻[14]提出了一種自適應濾波算法,它在進行狀態估計的同時還可以通過量測輸出在線實時地估計系統的噪聲參數。但筆者認為要同時對所有的噪聲參數進行自適應估計一般是不可能的。實際上,系統噪聲均值qk和量測噪聲均值rk都可以增廣等效為待估計的系統狀態,通過可觀測性分析判斷能否進行自適應估計,如果不可觀,則進行自適應濾波處理必然是無效的。因此,自適應濾波需要解決的主要問題是辨識系統噪聲方差陣Qk和量測噪聲方差陣Rk。系統噪聲屬于系統的固有特性,一般不易發生改變,即使有些變化,通常只要設置大致準確即可,相差3~5倍往往也不會對濾波估計結果造成太大的影響。在實際濾波應用中,微小的精度提高是次要的,系統工作的穩定性和可靠性才是更重要的,因而一般沒必要對系統噪聲作自適應處理。量測噪聲主要由外部因素引起,容易發生變化且有可能變化較大,有必要采用自適應濾波處理,因而量測噪聲方差陣Rk自適應濾波算法是實際中最常用的方法,其算法可表示為
(18)
(19)
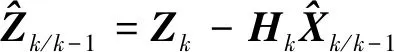
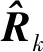
Kalman濾波的噪聲自適應效果與隨機系統的可觀測性密切相關。對于可觀測性很強的系統,對部分噪聲進行自適應處理是有可能實現的;但如果系統可觀測性本就比較弱,還要進行噪聲自適應就有可能比較困難了。在慣導/衛導組合導航中,根據位置或速度量測,要濾波估計陀螺漂移,特別是高精度的方位陀螺漂移,往往需要比較長的時間才會有估計效果,因此針對陀螺噪聲的自適應處理基本上是不可行的。
強跟蹤濾波也可以看作是一種自適應濾波方法,文獻[15]給出了強跟蹤濾波的理想特性:1)較強的關于模型參數失配的魯棒性;2)較低的關于噪聲及初值統計特性的敏感性;3)極強的關于突變狀態的跟蹤能力,并在濾波器達到穩態時仍保持這種能力;4)適中的計算復雜性。然而筆者認為強跟蹤濾波存在理想是很理想的,但現實是很現實的問題,其在線自適應調整Kalman濾波增益使得輸出殘差序列正交的目標是完美的,但在實際應用中具體操作方法卻是很難實現的,特別對于高維數的系統而言。此外,在強跟蹤濾波中并沒有考慮量測異常的影響,如果量測出現異常,則迫使狀態跟隨異常量測變化的思路是極不合適的。
在強跟蹤濾波中,漸消因子的選取有單重和多重之分。單重漸消因子將所有量測和狀態作為整體處理,使得所有狀態總體上跟隨量測的變化,即使沒有突變的狀態也會受到不良量測的影響。多重漸消因子考慮了不同狀態之間的突變差異,分別分配以不同的比例系數,越不易變化的狀態比例系數越接近1,越易變的越大于1,但多重漸消因子依然跟隨量測的整體變化。為了更加細致地區分不同量測的影響,筆者曾提出了基于序貫濾波的多重漸消自適應濾波方法[1]。在強跟蹤濾波中,若選取較少的漸消因子則求解簡單,但也存在明顯的缺陷;若漸消因子多,雖適應性強,但設計復雜,特別對于高維系統,要設計出合適的漸消因子參數矩陣是非常困難的,這是強跟蹤濾波的一大弊端或不實用之處。針對強跟蹤濾波的有效性驗證,研究控制方面的文獻選取的例子通常是比較簡單的低維系統,可能容易產生效果[16];但對于研究組合導航方面的高維例子,很多論文中展示的效果是讀者難以復現的[17],從而導致論文研究很多,實際應用卻幾乎沒有。
組合導航強跟蹤濾波性能與量測故障檢測需求之間是相互矛盾的。強跟蹤往往要求系統狀態估計快速跟蹤量測的變化,但量測快速變化有時是由故障引起的,雖然巨大變化的野值型故障容易被檢測并被隔離掉,但稍微偏離正常值的量測就會讓強跟蹤濾波與故障檢測算法無法同時滿足,過分強調強跟蹤性能必然損失故障檢測能力,有引入錯誤的風險;而過分強調故障檢測能力就會損失強跟蹤性能。在實際應用中,總是以系統可靠性為首位的,狀態一般不會發生突變,例如以高精度慣導的陀螺漂移估計為例,陀螺漂移對系統的影響微小,其估計過程必然是一個漫長的累積過程,不可能在短時間的量測突變中完成狀態估計,如果因突變而產生錯誤的估計反而會對系統造成更大的負面影響。
8 聯邦濾波問題
標準Kalman濾波的計算量與狀態維數的三次方成正比,計算量因狀態維數增加而急劇變大。一個復雜的大系統往往包含眾多的狀態變量,但大系統通常可以分解成若干子系統,并且在子系統中可能還存在一個關鍵的公共參考系統。例如慣導/衛導/里程儀/氣壓高度表組合導航系統就是這樣的一個典型系統,它以慣導系統為主要參考導航系統(假設無故障),其他三種導航子系統在正常工作時輔助慣導,以提高系統總體導航精度,當某一系統出現故障時將被監測和隔離,以免影響系統的總體性能。針對這類大系統,可以設計一個高維的綜合濾波器,包含所有狀態變量,再進行Kalman濾波,這一處理方式通常稱為集中式濾波;也可以采取所謂的聯邦濾波方法進行分散降階處理,采用聯邦濾波有利于降低各子系統的計算量,還便于各子系統的故障診斷和隔離,避免有故障的子系統影響整個濾波器,提高總體性能。
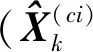
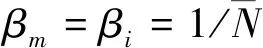
在聯邦濾波中,如果所有子濾波器的狀態均為公共狀態,則全局狀態融合精度與集中濾波器精度相同,結果均是最優的,且最優性與信息分配系數βi的選擇無關。但是當某些濾波器存在私有狀態時,聯邦濾波的精度一般低于集中濾波,這時聯邦濾波是一種次優濾波算法。
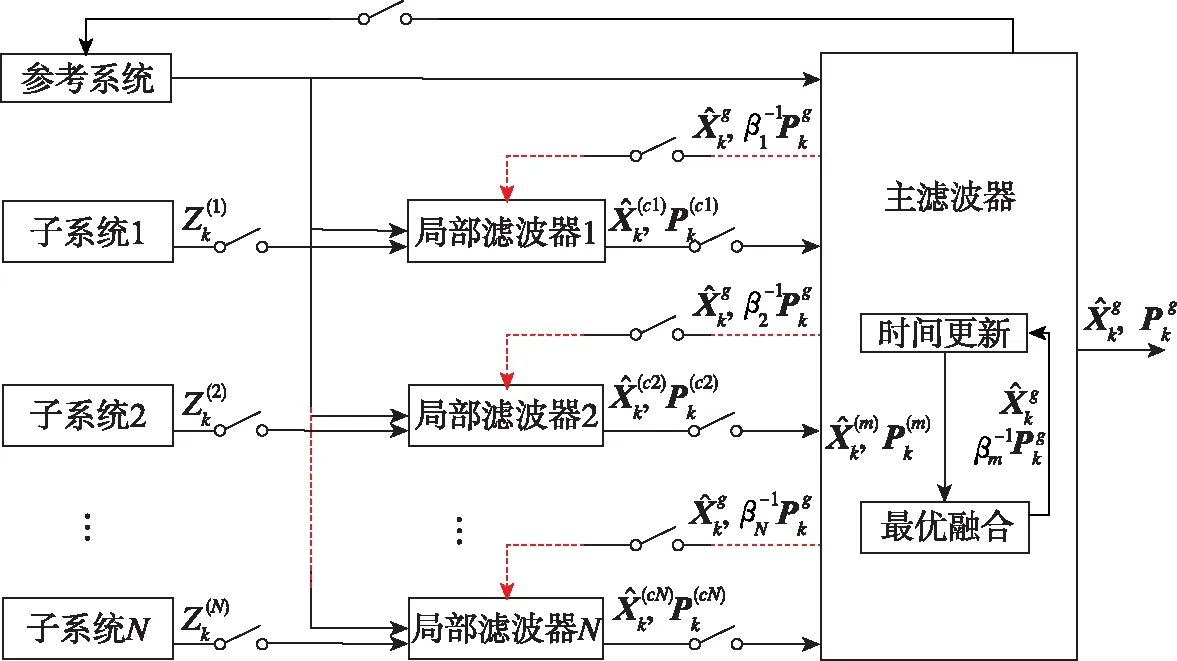
圖1 聯邦濾波示意圖Fig.1 Schematic diagram for federated Kalman filtering
Carlson在提出聯邦濾波時曾聲稱聯邦濾波器已被美國空軍的容錯導航系統“公共卡爾曼濾波器”計劃選為基本算法[19],但從目前組合導航系統的發展情況看,歷經30余年實踐該算法并沒有明顯的優勢,未獲得廣泛的實際應用。既然聯邦濾波實際用途不大,那么針對信息分配系數的所謂最優性研究也就沒什么意義了[20-21]。
針對目前常用的車載慣導/衛導/里程儀組合導航系統,或許是工程師們沒有領悟到聯邦濾波的精妙之處,據筆者所知并沒有實際產品采用聯邦濾波方案,而一般是采用三者的兩兩組合構成3個子組合導航系統,即慣導/衛導、航位推算/衛導和慣導/航位推算。在衛導信號有效時,慣導/衛導、航位推算/衛導組合工作,濾波估計慣導誤差及里程儀與慣導之間的安裝偏差角和里程儀刻度系數誤差,以慣導或航位推算的輸出作為系統輸出,并沒必要再將2個濾波器進行信息融合;在衛導信號短時間無效時,以純慣導導航作為系統輸出;在衛導信號較長時間無效時,慣導/航位推算工作,這時航位推算能夠有效抑制慣導誤差隨時間發散,導航輸出精度主要取決于航位推算精度。
9 非線性濾波問題
標準Kalman濾波僅適用于線性系統。對非線性系統作濾波估計,最常用和有效的方法是先進行泰勒級數展開,略去高階項后近似為線性系統,再進行線性Kalman濾波。這種處理方法稱為擴展Kalman濾波(Extended Kalman Filtering,EKF),或稱推廣Kalman濾波。如果對非線性系統作泰勒級數展開并保留二階項,則稱為二階Kalman濾波。不像確定性系統的二階泰勒展開比一階展開精度高一階,即前者誤差為O3而后者誤差為O2,二階濾波的精度并不明顯比一階EKF精度高,反而是對于高維系統而言,二階濾波的計算量增加了許多,因此二階濾波的性價比很低,并不實用。對于部分非線性系統,主要針對濾波時間更新過程,有時簡單地采用降低更新周期的辦法就能有效降低非線性的影響。
EKF采用解析方法進行一、二階矩概率統計特性的近似傳播,當系統非線性函數的雅可比矩陣求解比較復雜時,研究者們提出了利用采樣點進行概率傳播的濾波方法,例如采用確定性采樣策略的無跡Kalman濾波(Unscented Kalman Filter,UKF)、中心差分Kalman濾波(Central Difference Kalman Filter,CDKF),以及基于隨機采樣策略的粒子濾波(Particle Filter,PF)等[22]。對于高維系統而言,粒子濾波計算量巨大,目前還難以在嵌入式導航計算機中應用;UKF和CDKF也鮮有實際應用的實例報道。在研究和解決傳統慣導/衛導組合導航問題時,為了引出非線性濾波而評價EKF因模型非線性或模型不準確會引起濾波發散,多數是存在夸張成分,或者沒用好基礎的EKF。
慣導系統的姿態(可用歐拉角、四元數或姿態陣表示)、速度和位置等導航參數滿足如下非線性微分方程組
(20)
(21)
(22)
式中,各符號含義詳見文獻[1]。如果直接對上述導航參數狀態作組合導航Kalman濾波估計,則稱為直接濾波方法。直接濾波法并沒有太大的優勢,因為導航參數方程組始終是非線性的[23]。一般應建立如式(8)所示的導航參數誤差方程,誤差方程具有良好的線性特性,可以直接使用線性Kalman濾波估計。相對于直接濾波而言,利用誤差方程進行組合導航Kalman濾波估計的處理方法稱為間接濾波,在估計出導航誤差參數之后,對計算導航參數進行校正便可獲得準確的導航結果。在間接濾波中,對于慣性級慣導系統,失準角通常為角分量級、速度誤差為1m/s量級、水平定位誤差為1km量級,即使是低精度慣導系統,失準角誤差最大為度量級,在短時間內(數十秒甚至幾分鐘)也可以將誤差傳播視為線性的。
基于速度誤差或位置誤差量測的慣導/衛導組合導航,速度和位置誤差都容易保持為小量,且在3個失準角誤差中由于天向重力的耦合作用,2個水平失準角的可觀測性都很強,它們在很短時間內便可獲得估計并校正使之成為小量,因而只有大方位失準角的非線性建模和濾波具有一定的必要性和實用價值。當失準角較大時,采用非線性建模和濾波方法,例如UKF或CDKF,即使濾波估計是二階精確的,但三階或更高階誤差總是被忽略的,換句話說,不論采取什么樣的非線性濾波方法,雖說比線性Kalman濾波精度更高,但總是存在高階截斷誤差。特別是在大失準角的情況下,如果僅僅采用輸出校正方式將難以實現狀態的最優估計。對于非線性濾波應用,為了提高估計精度,在濾波估計過程中宜采用狀態反饋校正措施,使失準角逐漸減小,使誤差傳播轉變為線性傳播。在線性模型條件下,非線性濾波方法與線性Kalman濾波相比沒有任何優勢,反而是非線性方法的計算量通常更大。因此,在大失準角情況下使用非線性濾波的主要目的在于迅速估計出粗略的失準角,可以不將慣性傳感器誤差列入濾波模型以降低維數,濾波過程中當失準角降低至比較小時,從大失準角非線性濾波方式轉到小失準角線性Kalman濾波方式會更加有效,降低計算量的同時還能達到最優濾波估計精度[24]。在實際應用中,絕大部分非線性組合導航問題都可以轉化為線性方法解決,且線性濾波方法更加穩定可靠。當然,在某些對時間要求比較苛刻的初始對準中,如果采用非線性粗對準+線性精對準兩段式對準的濾波時間太長,可以改用數據存儲與逆向導航技術,有利于縮短對準時間和提高對準精度[25]。
10 可觀測度分析問題
在現代控制理論中,確定性系統的可觀測性是指由一段量測輸出確定系統狀態的能力,它屬于定性的描述,對于某一狀態或狀態組合,要么可觀測要么不可觀測。定常系統的可觀測性分析,可以使用可觀測性矩陣進行判斷,方法簡單;但是時變系統的可觀測性分析通常比較復雜,難以簡單而有效地給出結論。
在Kalman濾波理論中,隨機系統的可觀測性概念與確定性系統略有區別,前者表示從一段量測中獲得系統狀態的無偏估計的能力。如果量測噪聲陣正定,隨機系統的可觀測性與相應確定性系統的可觀測性結論恰好一致。對于隨機系統,僅僅進行定性的可觀測性分析是不夠的,顯然,不可觀測的狀態分量肯定不會有濾波估計效果。但對于可觀測的狀態分量,即便獲得了該狀態的無偏估計(一階矩),然而其均方誤差(二階矩)還是存在大小差異的,均方誤差可以看作是Kalman濾波估計精度的定量描述,它隨時間的變化正體現了濾波器的收斂速度。
針對系統狀態向量中的每一個分量Xk(j)(j=1,2,…,n),定義它的可觀測度如下[26]
(23)
由此可知,可觀測度是針對某一狀態分量在某一時刻而言的,其含義是某一狀態分量的初始設置誤差的標準差P0(jj)與同一狀態分量在k時刻的濾波誤差標準差Pk(jj)的比值。可觀測度為無因次量,在數值上越大,表明在經過一段時間Kalman濾波后,相應狀態分量的估計誤差下降程度越顯著,或者說精度提升效果就越明顯。根據經驗,可人為設置如下閾值大致判斷狀態分量Xk(j)的可觀測度強弱
(24)
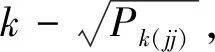
對于時變隨機系統的可觀測度分析,文獻中常討論的方法有分段線性定常系統(Piece-Wise Constant Systems,PWCS)方法[27-28],通過分析系統的提取可觀測矩陣(Stripped Observability Matrix,SOM)的奇異值或條件數,判斷系統狀態的可觀測度[29-32]。實際上,那些方法是存在本質缺陷的,它沒有考慮到系統噪聲的影響,相當于把系統當作確定性系統看待,舉一特殊的隨機定常系統例子,如下
(25)
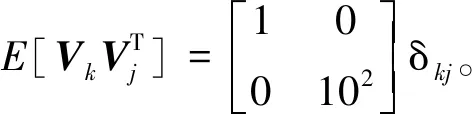
文獻[33]給出的基于Kalman濾波均方誤差陣Pk的特征值和特征向量的可觀測度分析方法才是非常合理的方法,它充分考慮了系統所有噪聲的影響,不只是量測噪聲Rk、還有系統噪聲Qk和狀態先驗噪聲P0都會對Pk產生影響。實際上,Pk的對角線元素的平方根正好代表了各狀態的濾波估計精度(均方誤差大小),這在Kalman濾波建模準確的情況下是必然成立的,如果實際應用時出現偏差,不應歸咎于該分析方法不適用,而應重新審視建模是否準確。對于狀態維數眾多的系統,不同類型狀態之間的物理含義是不同的,一般不能相互比較濾波估計精度,例如慣導/衛導組合的速度誤差和定位誤差之間,但同類誤差之間是具有可比較性的,例如東向、北向和天向速度誤差之間。若對均方誤差陣Pk作特征值分解,特征向量往往表示一些狀態的線性組合,它們不一定表示相同的物理量,因此通過比較特征值的大小來確定狀態組合的可觀測度,其物理意義不夠明確。其實,最簡單和最合適的方法就是直接選取Pk的對角線元素的平方根作為相應狀態的可觀測度,且同類物理量狀態之間可直接進行比較。
最后指出,PWCS可觀測度分析方法宣稱無需濾波就能獲得系統狀態的可觀測度,計算量小。事實上PWCS方法是粗略的,慣導/衛導組合的可觀測度與載體具體的運行軌跡(機動狀況與持續時間長短)密切相關,PWCS分段越少精度越差,有可能忽略了一些重要的運行細節,只有當PWCS分段時間無限短時(同于Kalman濾波時間更新周期)其結果才是精確的,與Kalman濾波均方誤差陣分析方法一致(僅是不考慮噪聲的情況下),這時并不存在計算量上的優勢。
11 均方誤差陣邊界限制問題
標準Kalman濾波是線性最小方差無偏估計,在系統建模準確的情況下,可以獲得狀態的最優估計。但是,在實際系統中,模型或多或少存在一些偏差,隨著濾波的推進,長時間后有些狀態的均方誤差會逐漸變小,特別是對于不受或少受系統噪聲影響的狀態,例如隨機常值狀態(陀螺隨機常值漂移或加速度計常值偏值)。均方誤差變得很小,理論上表示所對應狀態的濾波精度很高,但實際上由于建模誤差或干擾影響,該狀態不可能達到相應的估計精度,從而出現了理論精度與實際精度之間的矛盾。這一現象在慣導/衛導組合的天向通道中表現得尤為明顯,由于天向存在重力耦合的影響,使得天向加速度計隨機常值偏值的可觀測度很高,短時間內就會獲得很好的濾波效果,均方誤差陣對應元素將快速收斂變得很小,但是,如果建模不準確,例如加速度計零偏會隨溫度緩慢變化,則均方誤差過度收斂后濾波器將難以再適應狀態的緩慢變化,產生濾波估計偏差。
解決濾波器均方誤差過度收斂的一種方法是采用虛擬噪聲注入技術,即人為加大系統噪聲,使得由于噪聲的不斷激勵作用,狀態估計均方誤差不至于過度收斂得太小。但加大系統噪聲后,可能帶來的不利后果是,如果長時間得不到量測更新,狀態估計均方誤差將變得很大,這也與實際情況不符。防止均方誤差過度收斂的另一種直接而有效的方法是[13],根據狀態的實際物理含義或經驗設置一定的均方誤差下限邊界Pmin限制(通常為對角陣),當濾波器量測更新均方誤差陣Pk的對角線元素小于Pmin對應下限值時,人為直接強制將其取為下限值,可用偽代碼表示為
fori=1,2,…,n
ifPk(i,i) Pk(i,i)=Pmin(i,i) end 這里一般不必考慮Pk非對角線元素的影響,總可保證Pk是對稱正定的。當然,均方誤差下界也不能設置得過大,否則會影響Kalman濾波估計精度,造成狀態波動。 類似地,也可以采用均方誤差陣上限限制措施,防止可能出現的濾波異常。只是上限邊界限制不能再簡單采用直接設置對角線元素的方法,因為這可能導致Pk不正定,而可采用如下方法 end 其中,Pmax為人為設置的均方誤差上限邊界對角陣,上述偽代碼式的含義是,當對角線均方誤差Pk(i,i)超過上限Pmax(i,i)時,將Pk的第i行和第i列元素都同時縮小s倍,顯然,也總能保證Pk是對稱正定的。 標準Kalman濾波基本公式在理論上非常完美且不復雜,在隨機系統建模理想準確的條件下,能夠得到系統狀態的最優估計,即線性最小方差無偏估計。但在實際組合導航應用中,系統建模或多或少存在誤差,也就使得實際應用時不存在理想最優的前提條件,研究者和工程師們在關注濾波估計精度的同時,更應關注實際應用時的濾波穩定性和可靠性。 導航技術是一門工程實踐性很強的技術。從技術傳承和工程應用的角度看,特別在組合導航的非線性濾波、強跟蹤濾波和聯邦濾波等幾個方面,建議熱心的研究者們在發表論文時能給出仿真部分的數據和代碼,供他人學習參考或改進,這樣才更有利于促進群體理論研究水平的提升和成果轉化。遺憾的是,目前許多論文的仿真結果是不可復現的,浪費了大量科研經費和讀者的時間精力,迫使讀者也即后繼的研究者又提出了看似效果更好的不可復現的所謂新方法,如此不斷反復,理論和仿真研究似乎非常完美深入,但卻鮮有實際應用。 不妨將經典Kalman濾波與經典控制領域的比例-積分-微分(Proportianl-Integral-Derivative,PID)控制做個類比。現代控制理論雖然取得了很大的發展,解決了許多經典控制理論不能解決的問題,但經典PID控制仍然應用最為廣泛,其原因在于:1)結構簡單、魯棒性和適應性好;2)大多數控制對象使用常規PID即可滿足實際需求;3)調節整定很少依賴于系統的具體模型;4)各種高級控制方法在應用上還不完善,難以被技術人員掌握。筆者認為上述描述也非常適合于傳統Kalman濾波與許多高級濾波方法的對比。研究者們在提出和仿真新濾波方法時往往過分強調了新方法的優勢,而忽略了傳統Kalman濾波方法通過細節上的簡單處理也可能實現同樣的效果,例如采用系統狀態反饋、狀態估計均方誤差陣(P)的方差限制或重置、系統噪聲方差陣(Q)的虛擬建模、量測噪聲方差陣(R)的自適應處理等措施。可以說,在許多場合僅需對PQR參數進行簡單調整,就能應用好組合導航Kalman濾波技術,取得良好的估計效果。 致謝感謝以下同行對論文初稿的審閱并提出寶貴的修改意見:付強文、翁浚、王茂松、張全、楊君、王文舉、匿名評審專家。
end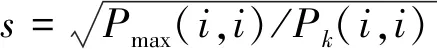
12 結論與建議

