基于碎片化學習的數學建模課堂教學研究

胡文燕

【摘要】《數學建模》是各高校數學專業的一門課程，一直以來深受廣大師生關注，但在課堂教學中卻存在著諸多問題.為充分調動學生主動學習，更快更好地提高線上線下相結合的混合式課堂教學的靈活性和教學效果，文章通過對數學建模過程中的模型假設、模型建立、模型求解進行探討，結合實踐教學經驗，將碎片化學習理念融入實際課堂教學中，并通過建模案例給出幾點教學建議.

【關鍵詞】碎片化;關鍵詞;建模目的;求解方法

【基金項目】山西省教育科學“十三五”規劃課題資助項目（GH-16107）;晉中學院教學改革與研究項目（Jg201914）;晉中學院“數學建模”優秀教學團隊資助項目;山西省高等學校教學改革創新項目（J2020319）

一、引 言

數學是一門基礎學科，它可以迅速地發展并滲透到各個新的專業和領域，為不同專業和領域的實際應用和問題研究提供合理有效的解決方案和解決方法，幾乎所有問題、所有課題的解決都離不開數學建模[1].但在實際教學中，卻存在著很多問題，學生對建模方法的掌握往往不夠透徹，有很多學生會覺得數學建模課程不像其他專業課程那樣系統，各章節之間也沒有承上啟下，環環相扣，而是整體表現得零零碎碎，相互獨立[2].

2020年初，突如其來的疫情打亂了各高校、各行業的既定步伐，為切實確保各高校全體師生的生命安全和學生的身體健康，各高校多次推遲了開學.在此期間，本著“停課不停教、停課不停學”的原則，各專業、各學科根據各自的專業特點，積極實行了線上網絡課堂教學.

與傳統教學相比，線上教學更加彰顯了學生的主體地位，而學生對線上教學的態度，直接影響到教學成效.線上教學更需要學生積極主動思考，自主查閱資料，分組研討，這也就要求學生投入大量的時間和精力.那么，如何充分引導全體學生發自肺腑地自主參與學習，如何充分調動全體學生的自主學習興趣和主動性就迫在眉睫，這也是研究性教學必須認真考慮的主要因素和問題.

二、數學建模課堂的教學探討

為了有效提高數學建模課程的實用性和教學效果，引導全體學生主動參與學習，只有從最根本的角度出發，讓全體學生真正掌握數學建模的基本方法，一切困難才能迎刃而解，這就要求教師在課堂講授的過程中，面對無從下手的問題，適時引導學生巧妙結合數學模型來自實際又有別于實際這個特性，將實際問題碎片化[3]，再一一擊破，最終找到建模過程中模型假設、模型建立及模型求解的突破點，并構建合理的數學模型.

（一）“關鍵詞”在模型假設中的作用

眾所周知，模型假設在整個建模過程中起著至關重要的作用，模型假設的必要和合理程度，直接關系到建模的成敗.[4]但在許多實際問題的建模過程中，學生往往是一頭霧水，尤其面對看似簡單的開放性題目，更是一籌莫展，無從下手.為了消除學生心中這種困惑，使他們面對實際問題能夠充分發揮想象力，給出合理全面的簡化假設，教師可以引導學生挖掘題目，將所給題目碎片化，找出題目語句中的所有關鍵詞，并針對關鍵詞逐個研究，結合題目中所給的實際問題，一一給出適當合理的假設.

現在以模型“椅子能在不平的地面上放穩嗎？[5]”和模型“雙層玻璃窗的功效[5]”為例具體闡述.

1.以“椅子能在不平的地面上放穩嗎？”為例

該問題只有短短幾個字，這會令大部分學生陷入迷茫，不知從何處下手，此時可將其關鍵詞一一列出，并逐一給出合理的簡化假設.

首先，“椅子”是這句話中的主語，是當之無愧的關鍵詞.生活中的椅子多種多樣，無論是材質還是形狀都各有不同，但若想建立數學模型解決這個問題，就必須對“椅子”做出明確、具體的假設.由題目所指，其關注的是椅子能否放穩的問題，故重點在于椅腳，而對椅面的形狀卻不必要求.結合實際情況，日常生活中的椅子大多是四條腿的，為簡單起見，可假設椅子有四條腿，并將椅子四條腿的長度看成完全一樣的.若將椅腳與地面接觸處視為一個點，并取規則的平面中心對稱圖形——正方形作為椅腳連線所構成的圖形，就可以巧妙地將“椅子”與“正方形”聯系起來，將實際問題用數學語言描述出來.

其次，“不平的地面”也是五花八門、各種各樣，甚至會有臺階這樣的情況出現.秉承合理簡單的原則，可將地面高度看成連續變化的，沿任何方向都不會出現斷裂，從而可將“不平的地面”視為數學上的連續曲面，并且它是相對平坦的.

最后，“放穩”這個關鍵詞是該問題的關鍵，為了能借助數學工具證明椅子能否在不平的地面上放穩，就必須用數學語言來描述“放穩”這個特征.因為當椅子穩穩地放在地面上時，其四只椅腳都是緊緊著地的，所以，可先假設椅子的椅腳只有三只腳同時著地，這樣就大大簡化了問題，并使得問題更加明朗.

2.以“雙層玻璃窗的功效”為例

乍一看這個題目不像是一個問題，不同于上一個模型是用問句呈現的，此處更像是一個標題.但其實不難想到，這個模型是要研究我們日常生活中常見的雙層玻璃窗的功效如何.

同前一個模型一樣，大部分同學會一頭霧水，不知道從哪里入手，這就需要我們一一找出關鍵詞，逐個攻破.

這里有三個“關鍵詞”：“雙層”“玻璃窗”和“功效”.先來看“雙層”：現實生活中，北方大部分城市建筑物的窗戶都是雙層玻璃的，也就是說窗戶上裝有兩層玻璃.細心觀察，會發現這兩層玻璃并不是緊緊挨在一起的，它們中間有一定的空隙.那么，這個空隙中有什么呢？毋庸置疑，是空氣.清楚雙層玻璃窗的結構以后，就要求我們在模型假設時，必須考慮雙層玻璃之間的距離，距離的選擇一定是最終玻璃窗功效的必要因素.

再看第二個關鍵詞“玻璃窗”：玻璃窗的安設目的是保暖，而市場上的玻璃五花八門，品種煩多，玻璃的材質不同，厚度不同，其保暖效果自然也就不同.那么，如何選擇玻璃，玻璃的材質、材質均勻程度和厚度對保暖效果又起到了多大的作用，都是我們需要研究的因素.

最后一個關鍵詞“功效”：指的是保暖效果到底有多好.結合物理學的知識我們知道，想要了解玻璃窗能多大程度的保暖，就是要研究熱量是如何在室內有取暖措施的情況下，通過玻璃窗流失的，這就涉及了物理學中熱量傳導的問題.制作工藝不同的玻璃，其各個點的熱傳導系數也不同，為簡單計，我們假設玻璃窗的玻璃材料均勻，熱傳導系數是常數.因為雙層玻璃窗不僅有玻璃，還有空氣，所以我們除了要研究玻璃的熱傳導以外，還必須考慮熱量通過空氣的傳導.

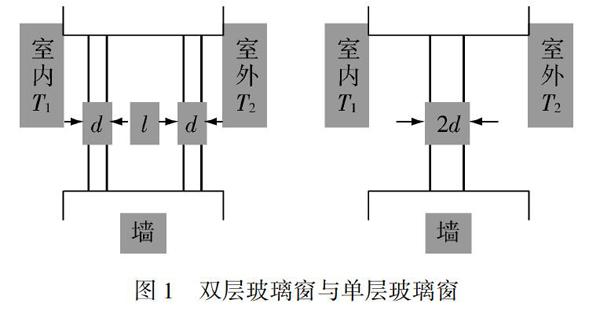
為了更好地突顯雙層玻璃窗的功效顯著，我們可以將其與單層玻璃窗進行比較，用數據說話.為了公平起見，可設單層玻璃窗的玻璃厚度是雙層玻璃窗玻璃厚度d的2倍，如圖1：

我們假設，雙層玻璃窗中間所夾空氣的厚度為l，為簡單計，假設窗戶的密閉性很好，兩層玻璃之間所夾的空氣是不流動的，也就是說，此處熱量的傳播過程只有傳導，沒有對流;室內、室外溫度分別為T1，T2，熱傳導已經處于穩定狀態，室內、室外溫度保持不變.這樣我們就順利地從三個“關鍵詞”入手，合理地對原問題進行了簡化，巧妙地將其用數學語言描述了出來.

（二）建模目的是模型構建的切入點

對問題有了合理的假設后，就需根據對象的內在規律建立數學模型，但在實際教學中，學生經驗不夠豐富，知識儲備不夠充足，往往不知從哪里入手，這就需要教師從模型建立的目的出發，一點一點引導，帶領學生找到模型建立的切入點.仍以模型“椅子能在不平的地面上放穩嗎？”和模型“雙層玻璃窗的功效”為例.

第一個模型“椅子能在不平的地面上放穩嗎？”中，“放穩”的意思可以很簡單地理解為椅子的四只椅腳同時著地，也就是四只椅腳與地面的距離都為零.而椅腳與地面的距離恰恰與椅子的位置有關，若我們能用正確的數學語言準確地描述椅子的位置，那么就說明我們可以把“椅子四只腳同時著地”的所有條件和所得出的結論都用正確的數學語言準確地表示了出來.

注意到椅腳連線呈正方形，而正方形是一個中心對稱圖形，當椅子位置發生改變時，正方形繞其中心旋轉的角度正好代表了椅子位置的改變，那么我們就可以用位置變量θ來描述椅子的位置.進一步地，可假設A，C兩腳與地面距離之和為f（θ），B，D兩腳與地面距離之和為g（θ），這樣我們就找到了模型建立的關鍵——數量指標，從而構建該實際問題的數學模型就變得非常容易了.

這個模型的巧妙之處就在于用變量θ表示椅子的位置，用θ的兩個函數表示四腳與地面的距離，而這都得益于對模型建立的目的這個切入點的分析研究.

第二個模型“雙層玻璃窗的功效”中，建模目的是通過比較單層玻璃窗和雙層玻璃窗的熱量流失，研究雙層玻璃窗的“功效”.

熱傳導過程遵循物理學中的物理定律：厚度為d的均勻介質，兩側溫度差為ΔT，則單位時間由溫度高的一側向溫度低的一側通過單位面積的熱量Q與ΔT成正比，與d成反比，即

Q=k（ΔT/d）.

接下來只需要分別求出雙層玻璃窗和單層玻璃窗各自單位時間通過單位面積的熱量，并進行比較即可.雖然一個房間的熱量流失不僅僅通過玻璃窗，還可以通過天花板、地面、墻壁等介質流失，但這個模型已經足夠證明雙層玻璃窗確實比單層玻璃窗在保暖方面更勝一籌，功效顯著.

由此可見，教會學生如何從建模目的出發找到模型構建的切入點是何等重要.

（三） 模型求解方法的選擇

數學模型的形式多種多樣，或者是數學公式、圖表、微分方程組，或者是一種算法，不同類型、不同形式的數學模型有著各自不同的求解方法，但也有一類數學模型，雖然模型形式相同，但有的模型變量特征不同，有的模型變量個數不同，有的模型建模目的不同，這時它們的求解方法也截然不同.

1.微分方程模型的求解

微分方程模型[5]是一類描述實際對象隨時間（或空間）演變過程，分析其變化規律，預測其未來性態的動態模型.經典的指數增長模型（Malthus模型）和阻滯增長模型（Logistic模型）都是以微分方程形式呈現的.

其中，x（t）為t時刻的人口，r為人口的固有增長率，xm為環境所能容納的最大人口數量.

這兩個模型構建的目的都是為預測t時刻人口的數量，故模型求解均是直接求微分方程的解，以此來預測人口.

但還有一類模型，雖也是以微分方程形式呈現的，但求解方法卻大不相同.以模型“種群的相互競爭[5]”為例，我們假設甲、乙兩個種群在各自獨立生存時，都遵從Logistic規律，那么t時刻兩種群的數量x1（t），x2（t）滿足：

其中r1，r2分別為甲、乙兩個種群的固有增長率，N1，N2是最大容量，單位數量的乙（甲）種群消耗供給甲（乙）種群的食物數量是單位數量的甲（乙）種群消耗供給乙（甲）種群的食物數量的σ1（σ2） 倍.

這個模型與Malthus模型及Logistic模型相比，形式是一樣的，都是微分方程，但因為該模型構建的目的是若干年后兩個相互競爭種群的演變結局，所以在對該模型進行求解時，并不需要直接對微分方程進行求解，而是運用微分方程的穩定性理論，直接研究其平衡狀態的穩定性，這也大大簡化了模型的求解.

由此可見，即便模型的形式是一樣的，但若是建模的目的不同，求解方法也是大不相同的.

2.數學規劃模型的求解

數學規劃模型[5]是一類優化模型，建立優化模型需要確定優化的目標和尋求的決策.實際生活中，很多問題歸結出的優化模型，其決策變量個數和約束條件個數一般都比較大，這樣就不能簡單地用微分法求解，需要用到數學規劃的方法.本文就典型的數學規劃模型——運輸問題和指派問題進行研究，探討其模型求解方法的不同.

運輸問題是線性規劃應用最廣泛的領域之一，以產銷平衡運輸問題為例，其數學模型形式如下：

該模型雖是一個線性規劃模型，但其結構卻具有特殊性，它含有m×n個變量，（m+n）個約束，約束條件系數矩陣的元素都等于0或1，模型的變量和約束均較多，故不適合用常規求解線性規劃模型的單純方法求解，而采用表上作業法求解這一類產銷平衡的運輸問題.

進一步，如果所有的決策變量不再僅僅是非負約束，而是0-1變量，又有模型中m=n，此時上述模型可寫為：

很顯然，這是典型的指派問題，它是一種特殊的平衡運輸問題，此處可將每個生產地的產量和每個銷售地的銷量都看作1，由于其結構的特殊性，不再用表上作業法，可用更為簡便的匈牙利算法進行求解.

再有，如果約束條件不全是等式，m≠n，建立0-1規劃模型是常用方法，由于任務的數量與能夠承擔的人員數量不一定相等，約束條件不再都是等式約束，故匈牙利算法不再適用，我們可以選擇Lingo數學軟件對其進行求解.

綜合上述，同樣都是數學規劃模型，如果變量個數不同，類型不同，或者約束條件不同，那么即便其形式很相似，求解方法也截然不同.這就要求教師在課堂教學中針對不同的數學模型，詳盡分析其模型形式，建模目的的異同，從而選取適合的求解方法.

三、 結 語

數學建模的教學一直是備受關注的重要課題，為了真正地將建模方法教給學生，教給學生如何真正地借助數學工具解決實際問題，就一定要認真鉆研教材、研究教法，從提高學生學習主動性出發，將碎片化教學理念巧妙融入實踐教學中，線上線下相結合，真正提高教學質量.

【參考文獻】

[1]唐婭嫻.數學建模思想對大學生數學應用能力的影響[J].科技經濟導刊，2017（8）：160.

[2]尹裴，關曉飛.數學建模課程教學實踐研究[J].教育教學論壇，2016（37）：75-76.

[3]郭亞娜，丁振國，李尚富.探究“碎片化”教學資源設計原則與建設 [J].科技展望，2016（35）：161-162.

[4]趙建昕.提高數學建模能力的策略研究[J].數學教育學報，2004，13（3）：50-51.

[5]姜啟源.數學模型：第四版[M].北京：高等教育出版社，2011.