導葉數對液力透平徑向力影響的數值分析*
畢智高,劉亞洲,相玉琳,馬楊愛
(1.榆林學院 化學與化工學院,陜西 榆林 719000;2.陜西省低變質煤潔凈利用重點實驗室,陜西 榆林 719000;3.延長油田股份有限公司 定邊采油廠,陜西 榆林 718600)
泵作透平(Pump as turbine,PAT)使用能夠將高壓液體的壓力能轉換為透平轉子的機械能,用來驅動發電機發電或耗能機械做功,從而實現對高壓液體能量的回收和利用[1]。目前在微小水電資源的開發利用、海水淡化、石油化工等節能技術領域有著廣泛的應用[2]。
具有螺旋形壓水室的葉輪式水力機械在偏離設計工況運行時以及由于誤差、實驗等各種因素,造成蝸殼內壓力軸對稱分布被破壞,會在葉輪上產生徑向力。徑向力會使葉輪式水力機械的旋轉軸受到交變荷載的作用,產生定向撓度,其大小直接影響到其工作穩定性。目前國內外專家學者對葉輪式水力機械徑向力的研究多集中于泵工況[3-7],而對透平工況的報道相對較少。新濱仁等[8]通過實驗測量了液力透平在設計工況和發生飛逸時的徑向力,研究了液力透平徑向力的表現與成因,發現液力透平徑向力的大小隨流量的增加而增大。楊軍虎等[9]通過數值預測發現相同流量下透平工況的徑向力比泵工況的徑向力一般要小。楊軍虎等[10]通過數值模擬研究了蝸殼結構對液力透平徑向力的影響,結果表明雙蝸殼液力透平的徑向力水平大于單蝸液力透平。楊軍虎等[11]采用數值計算的方法分析了氣液兩相介質時液力透平的徑向力,結果表明兩相流時透平的徑向力隨著流量的增加而逐漸增大,隨著氣體體積分數的增大而逐漸變小。Gonzáxlez等[12]通過數值計算研究表明大外徑葉輪將產生更大的徑向力。
文獻[13]表明能夠通過導葉加蝸室的結構來平衡葉輪上的徑向力,但這僅指大型單級泵,沒有說明是否適用透平工況,也沒有給出導葉的結構與導葉的葉片數等詳細信息。
針對上述問題,作者在已有研究工作的基礎上,通過在葉輪進口增添不同葉片數的導葉進行數值計算,研究導葉數對液力透平徑向力的影響,為改善透平的運行性能提供一定參考。
1 液力透平基本參數
以比轉數ns=41的單級離心泵為研究對象。泵工況設計參數為轉速n=2 960 r/min,流量Q=52 m3/h,揚程H=101 m,效率η=60.9%,軸功率N=23.5 kW,葉輪旋轉方向為逆時針。PAT使用時按文獻[14]提出的方法在葉輪進口添加導葉。透平主要幾何參數為葉輪出口直徑D1=68 mm,葉輪進口直徑D2=285 mm,葉片出口安放角β1=30°,葉片進口安放角β2=28°,葉片數Z=5,葉輪出口寬度b2=6.5 mm,蝸殼進口寬度為b3=18 mm,蝸殼基圓直徑D4=390 mm,蝸殼進口直徑D5=58 mm,導葉葉片數Z0=6、8、10,導葉弦長l=143 mm,導葉高度h=6.5 mm。
2 徑向力數學模型
透平葉輪與導葉耦合面為圓柱形側面,假定每個微元耦合面ΔS上的靜壓均勻分布,則包含第i個網格節點微元耦合面上的壓力Fi為
(1)
應用力的分解合成定理,將Fi分解為x和y2個方向上的作用力 。
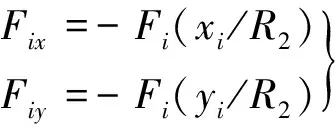
(2)
則徑向力在x向和y向的分量Fx和Fy為

(3)
因此,作用于耦合面上總的徑向力為
(4)
θ=arctan(Fx/Fy)
(5)
式中:R2為葉輪進口半徑;pi為第i個網格節點的壓強;xi、yi為包含第i個網格節點的三維坐標;θ為徑向力和y向夾角。
3 計算模型
3.1 三維造型與網格劃分
應用Pro/E軟件對蝸殼、導葉及葉輪等流動區域三維造型,為適應葉輪、蝸殼等過流部分復雜的幾何形狀,應用ICEM軟件對模型進行非結構四面體網格劃分。以6葉片導葉透平為例,模型網格見圖1。
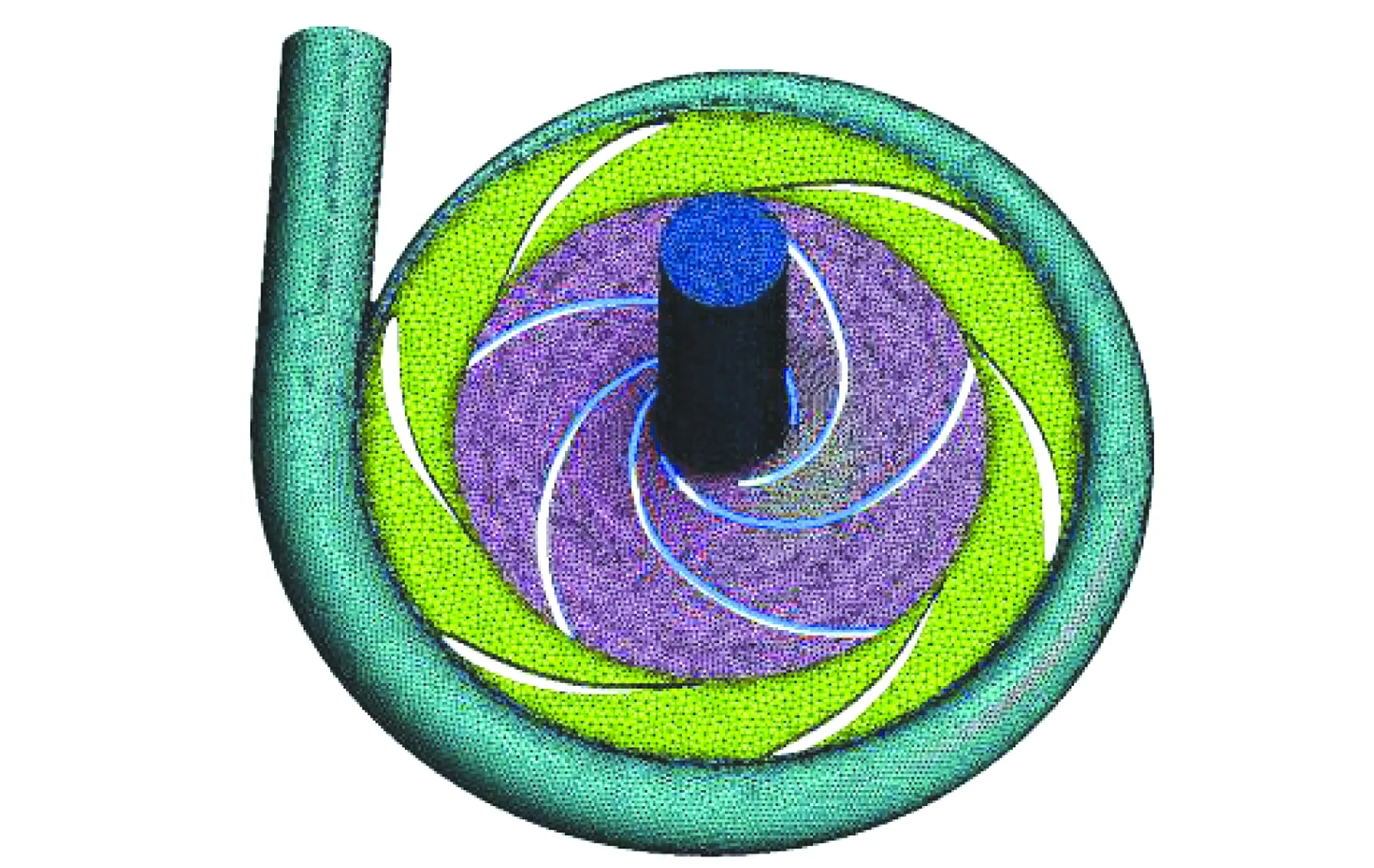
圖1 模型網格
3.2 邊界條件
數值模擬計算設置蝸殼區域為固定坐標系,葉輪區域為旋轉坐標系的多重參考坐標系。邊界條件設置如下。
(1)質量進口邊界。
(2)壓力出口邊界,流程工業中為保證液力透平驅動的后續裝置正常運轉,消除透平運行可能產生的汽蝕危害,一般要求透平出口有(400~600) kPa的余壓,因此將余壓設置設為500 kPa,以達到后續工藝要求。
(3)壁面條件:固壁處采用無滑移邊界條件,對于近壁處流動區域采用標準壁面函數法。
通過改變進口質量流量的大小來模擬液力透平在不同工況下的流動情況。
3.3 控制方程及湍流模型
采用時均、不可壓Navier-Stokes方程描述流場內部流動;選用標準k-ε湍流模型,壓力-速度耦合求解方式選用SIMPLEC算法,即壓力速度修正方法,計算精度為10-5,所輸介質為常溫清水。
4 結果與分析
4.1 外特性曲線
根據數值計算結果可以直接提取不同工況時液力透平的進出口總壓pin和pout,由式(6)求得透平各個工況下的壓頭。
(6)
式中:H為透平壓頭,m;pin為進口總壓,Pa;pout為出口總壓,Pa;ρ為介質密度,kg/m3;g為重力加速度,m/s2。
根據透平葉輪繞其旋轉軸的力矩之和M,由式(7)可以得出透平軸功率P,由式(8)可以得出水力功率P′。
(7)
P′=ρgQH
(8)
式中:n為葉輪轉速,r/min;M為葉輪轉矩,N·m;ω為葉輪旋轉角速度,s-1;Q為流量,m3/s。
據式(9)可以計算出透平的水力效率ηh。
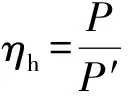
(9)
由(6)~(9)式可得到透平的壓頭、功率和水力效率。
不同導葉數液力透平最高效率工況時的性能參數見表1,不同導葉數透平的外特性曲線見圖2~圖4。
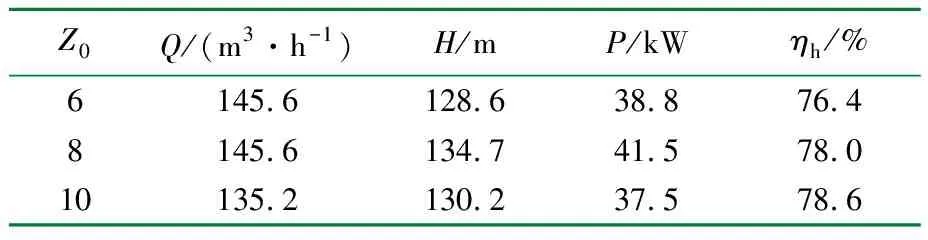
表1 液力透平最高效率點性能參數

Q/(m3·h-1)圖2 壓頭-流量曲線
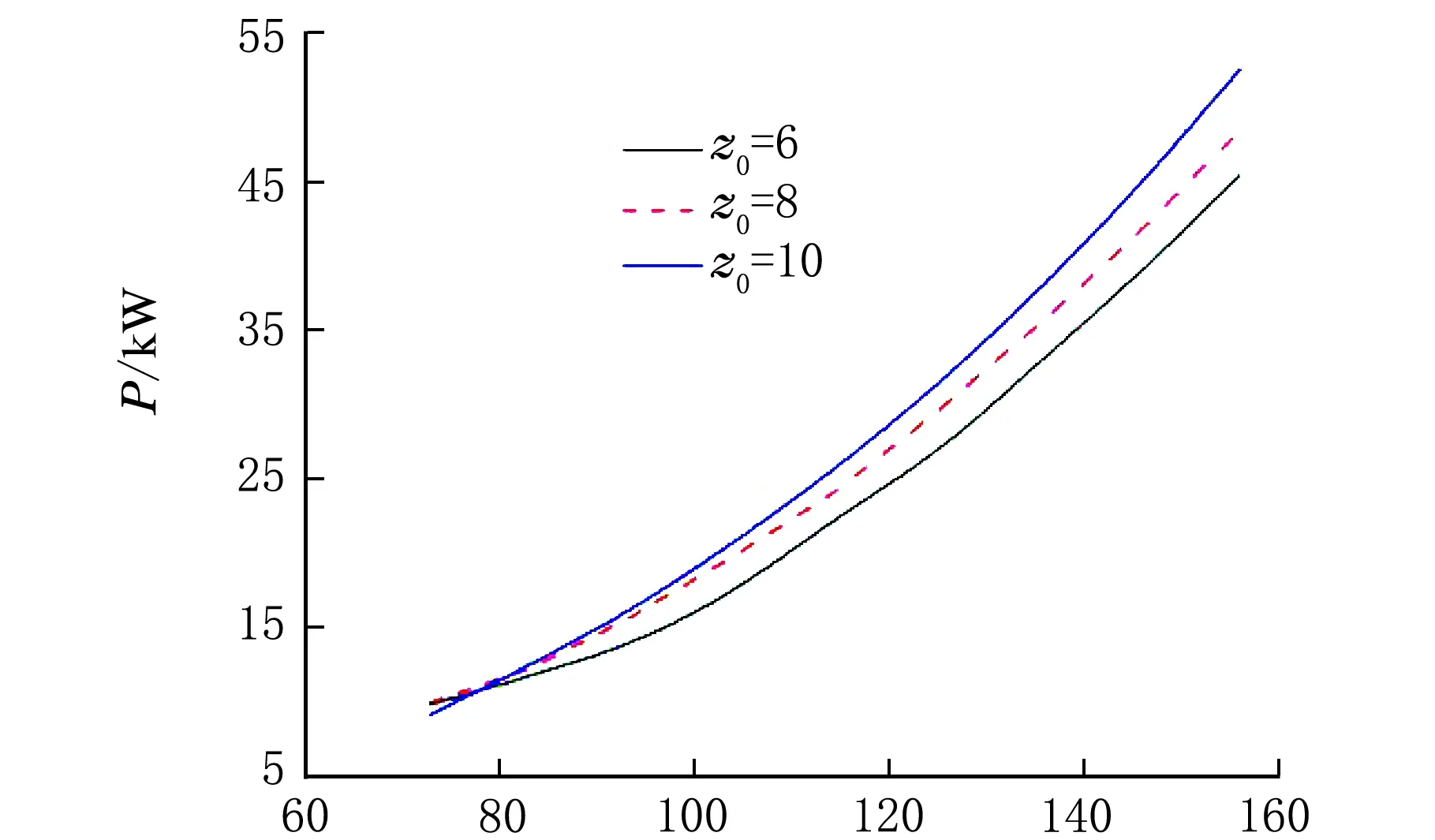
Q/(m3·h-1)圖3 功率-流量曲線

Q/(m3·h-1)圖4 水力效率-流量曲線
液力透平外特性是內部流場的外在表現,對比圖表可以看出,透平可回收的壓頭和功率均隨著流量的增加而增加大,即只有當透平的流量增加到一定臨界值時才會有功率輸出,未達到臨界流量時,流體能量主要用來克服機械摩擦,要讓透平產生較大功率輸出就必須使其增大流量運行。透平的效率隨著流量的增先增加大后減小;相同流量下,導葉數越多,透平可回收的水頭、功率和水力效率也越大,相對6葉片導葉透平,8導葉和10導葉透平最高水力效率分別提高了1.6%和2.2%。
4.2 靜壓分布
最優工況下不同導葉數的液力透平中截面壓力分布云圖見圖5。
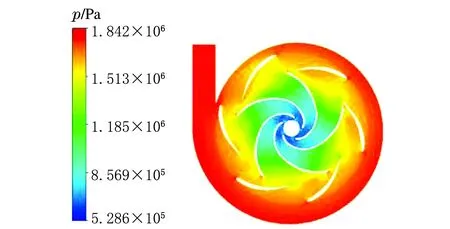
a Z0=6
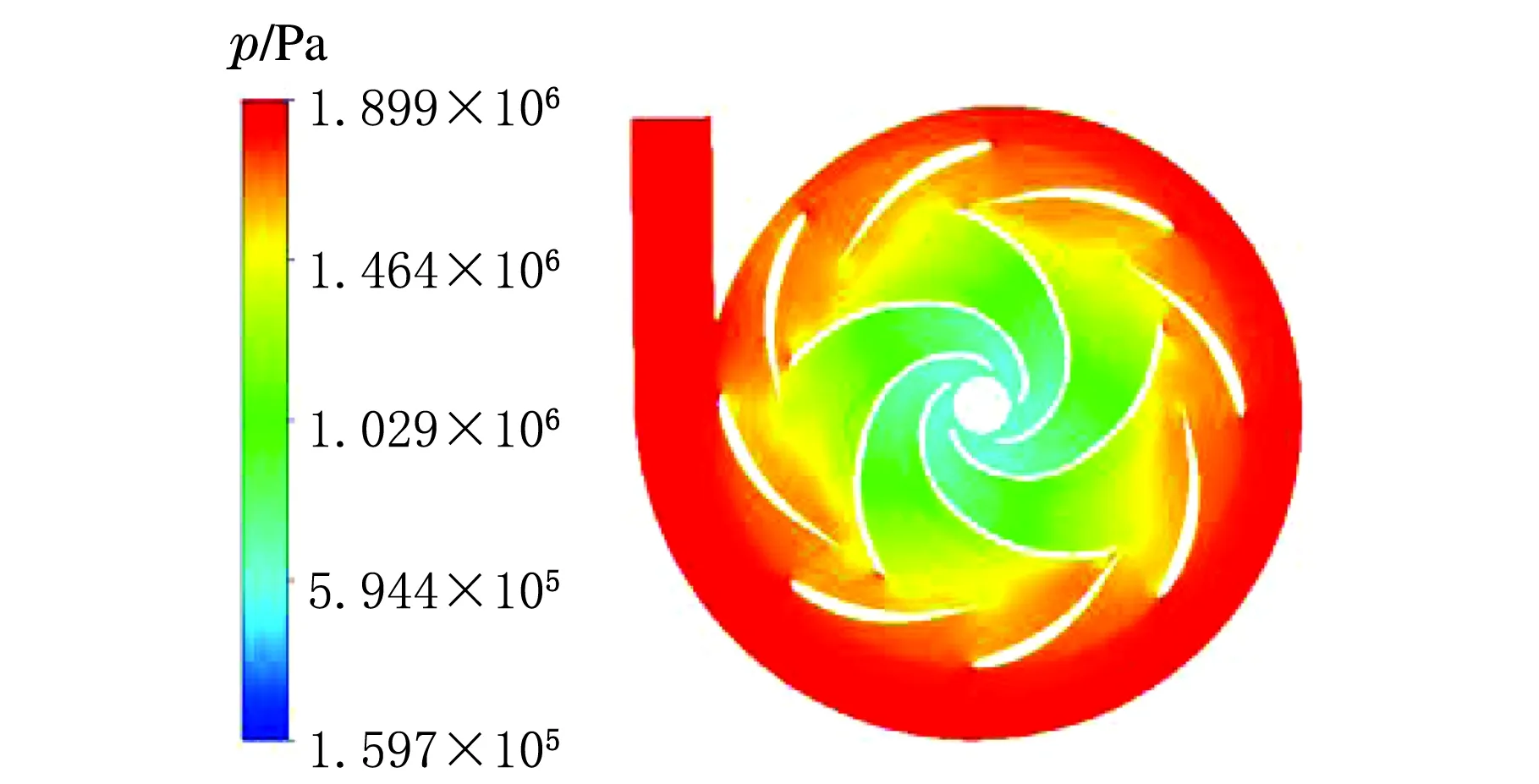
b Z0=8
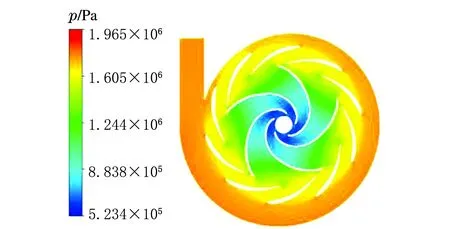
c Z0=10圖5 液力透平靜壓分布
由圖5可知,透平內部的靜壓值沿流道從進口到出口逐漸降低,符合做功原理;靜壓最低值出現在葉片吸力面靠近葉輪出口處區域;靜壓值從導葉進口到出口逐漸減小,表明導葉的導流作用能夠將流體的壓能轉化為動能;不同導葉數透平葉輪各流道間的壓力分布不同,10導葉數透平葉輪各流道間的壓力分布對稱性最好。可見,透平增加恰當葉片數目的導葉運行可以改善葉輪受力的對稱均勻性,有益于提高透平運行的穩定性。
4.3 徑向力分析
不同導葉數液力透平所受徑向力的大小見圖6。
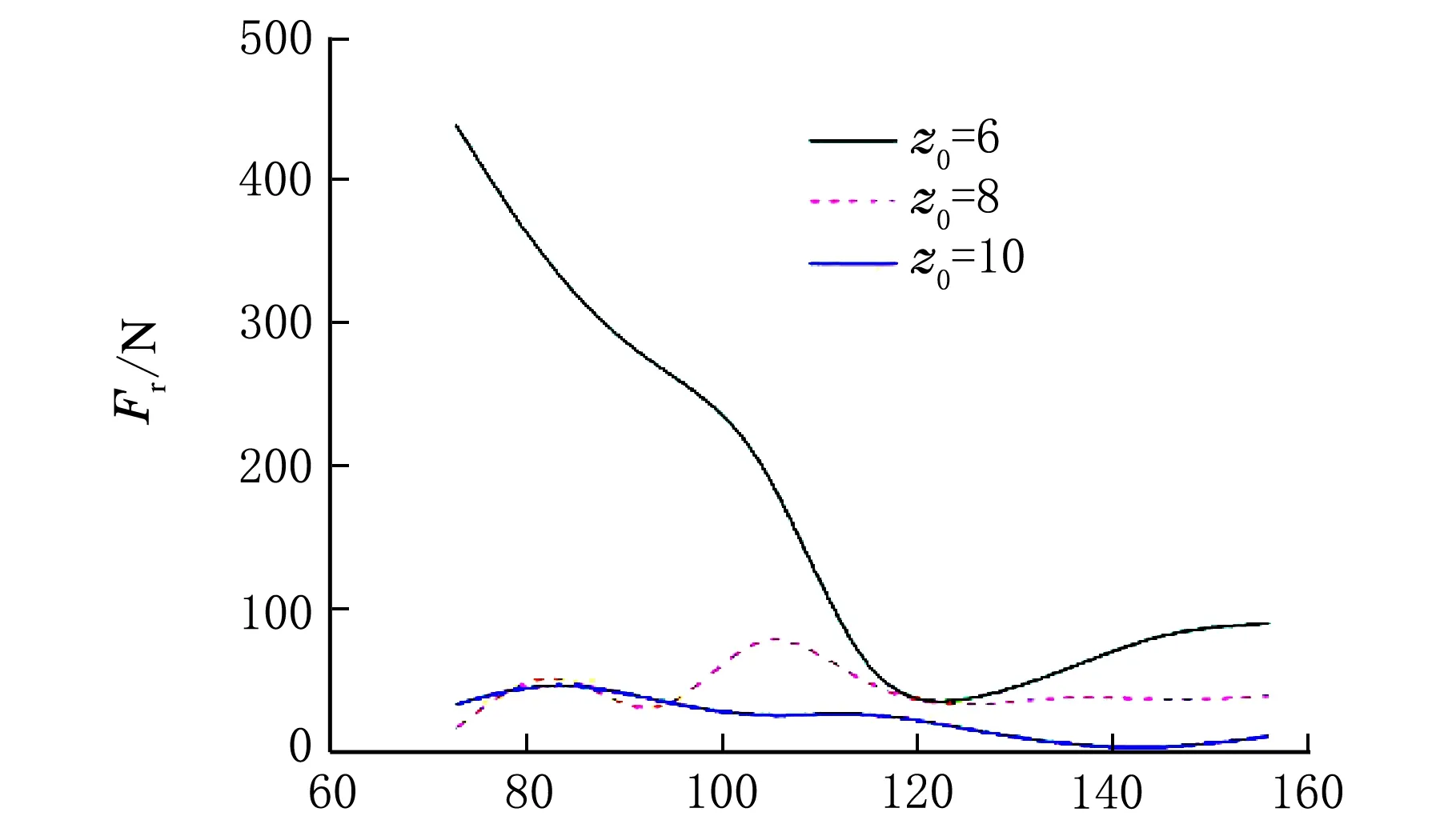
Q/(m3·h-1)圖6 徑向力大小
由圖6可知,各工況下葉輪均存在徑向力;導葉數越多,葉輪所受徑向力越小,10導葉透平葉輪所受徑向力小于40 N;6導葉透平所受徑向力大小變化最大,10導葉透平葉輪受徑向力大小相對最穩定。
徑向力的方向見圖7,β為沿流體流向葉輪所受的徑向力與隔舌之間的夾角。10導葉透平徑向力的方向為50°~240°,變化范圍相對最小。
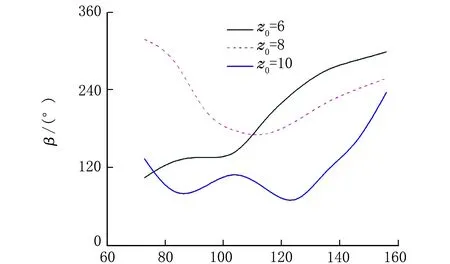
Q/(m3·h-1)圖7 徑向力方向
4.4 葉輪進口靜壓力
葉輪、導葉耦合面周向Z=0位置處在小流量、最優流量和大流量工況的靜壓分布見圖8。
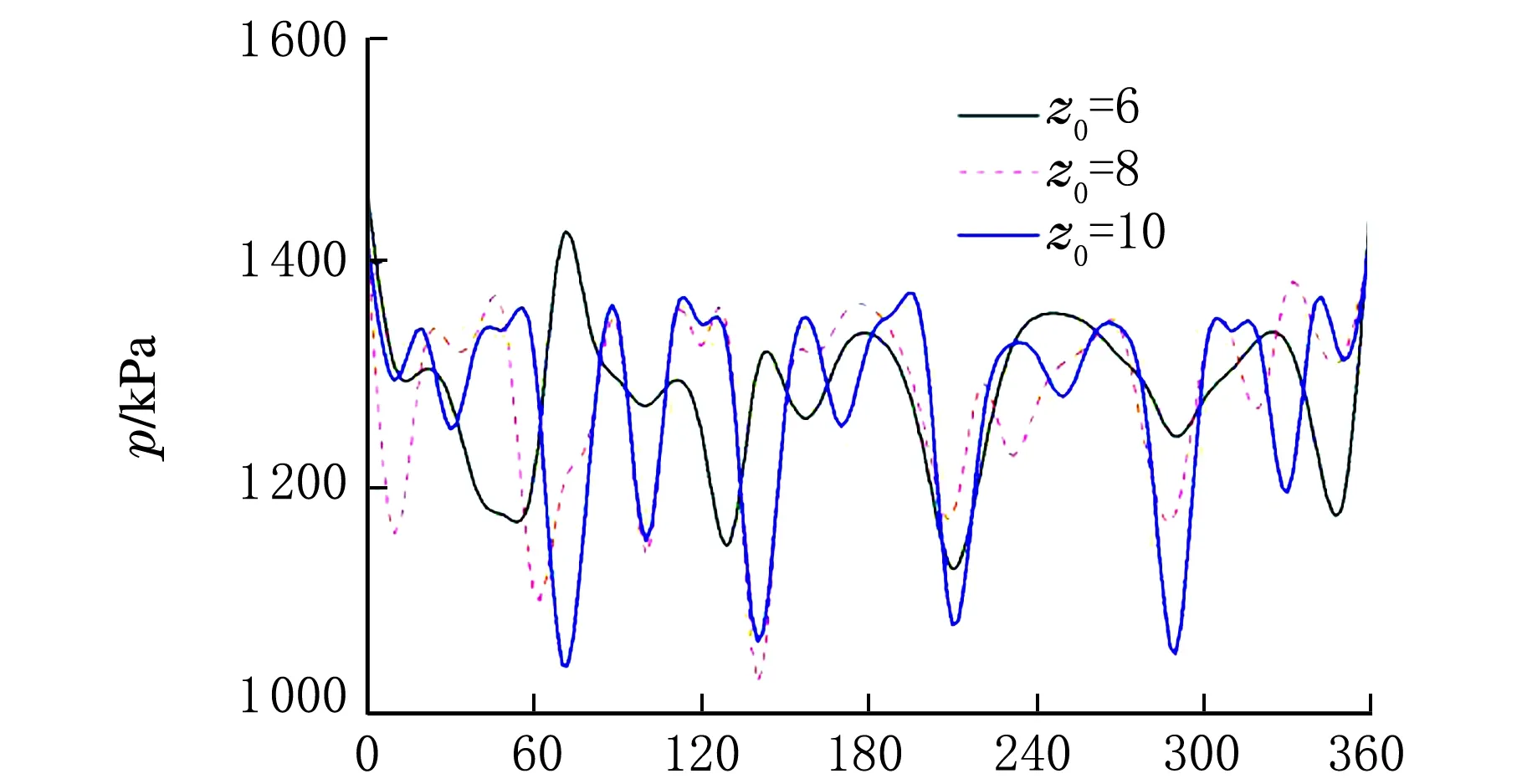
θ/(°)a 小流量

θ/(°)b 最優流量
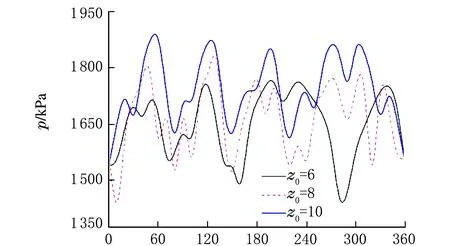
θ/(°)c 大流量圖8 葉輪導葉耦合面靜壓分布
由圖8可知,葉輪進口靜壓分布整體上趨于一致,呈脈動狀;各工況下透平葉輪進口靜壓沿圓周分布都不均勻,且局部存在高壓區,相差180°位置處的靜壓只能部分抵消,這導致了徑向力的產生;隨著流量的增大,葉輪進口圓周上脈動靜壓差也隨之增大,10導葉透平在大流量工況時葉輪進口靜壓值增浮比較顯著。
5 結 論
(1)液力透平的壓頭和功率都隨著流量的增大而增大,效率隨著流量的增加先增加大后減小;相同流量下,導葉數越多,透平可回收的水頭、功率和水力效率也越大;
(2)導葉數越多,葉輪所受徑向力越小,10導葉液力透平葉輪所受徑向力大小相對最穩定;透平在含有恰當葉片數的導葉下運行,能夠有效平衡葉輪所受徑向力,有助于透平穩定運行。

