將數學史與數學本體知識巧妙融合

劉燦文 楊懿荔

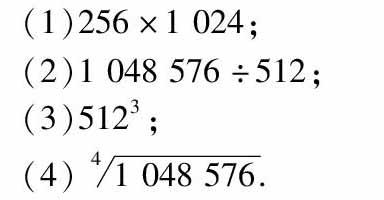
【摘要】現行教材對“對數的概念”的引入過于直接，一般教學方式對“對數的運算”的處理也接近于強加式，它們均不利于培養學生的數學素養及學習興趣.為此，筆者將對數的概念與對數的運算整合在一節40分鐘的教學課中，在“數學史與數學本體知識巧妙融合”的理念指導下生成教案，努力讓學生了解對數概念的起源與發展，并給予學生探索對數運算性質的機會.

【關鍵詞】數學史;數學本體知識;對數的概念;對數的運算

一、教學背景

對數思想的產生大大簡化了煩瑣的大數運算，對天文學的發展提供了極大的幫助.而在現行的上教版高中數學教材[1]中，對數概念的引入是從一個指數方程入手，并沒有闡述其背后的人文因素與實際的迫切需求.這必然導致學生在學習過程中產生困惑：為何要學習對數？發明對數的意義何在？在數學史融入數學教育的啟發下，越來越多的數學教師意識到上述問題，筆者也不例外.

為幫助學生解決上述困惑，筆者對“對數概念的引入”進行教學重構，將數學史融入教學，努力讓學生走進歷史，身臨其境，體會發明對數的必要性.只有學生切實體會到對數為簡化計算帶來的極大便利，學生才不會覺得對數只是為了和指數式進行互化、只是一個枯燥無聊的計算工具，從而使學生感悟數學之美.

任何概念的完善都要經歷產生與發展這樣兩個階段，對數亦是如此.因此，本節課的教學目標除了學習對數概念以外，學習對數的運算也是一個重頭戲，兩者不可分割.在現行教材中，對數的概念、對數的運算這兩部分內容的教學各需要一節40分鐘的課，現在，為了更好地向學生呈現對數的產生與發展過程，筆者需要將對數的概念與對數的運算整合在一節40分鐘的教學課中.在著手整合之前，筆者考慮到：首先，如果花費太多時間在對數概念的引入上，雖然可以將對數的產生過程復原，學生也能很好地理解對數發明的必要性，但是對數的運算部分的教學就會變得非常倉促，也許只能引出對數的加法性質（性質1），而減法性質（性質2）與乘法性質（性質3）只能作為思考題讓學生課后完成，這樣一節課就不再完整了.其次，對數的三大運算性質在教材中憑空出現，缺少來龍去脈，這顯然不符合學生的邏輯認知規律，這樣的教學過程是不自然的，教師應當對此加以適當的鋪墊.基于上述考慮，在“對數概念及其運算”（1課時）教案的生成過程中，應當努力達成以下三個目標：

目標1 借助數學史與數學教育（HPM），引入對數的發展過程，讓學生了解對數概念的誕生與起源;

目標2 利用實例，讓學生自發地探索對數的運算性質，使教學過程自然且有邏輯，避免蒼白的強加式教學;

目標3 合理分配時間，對于目標1、目標2做到細致且不拖沓，精確且高效.

二、教學過程與教案生成

（一）課前引入

在課前，要求學生在不借助計算器的前提下進行一些大數的乘法、除法、乘方、開方運算，讓學生體驗到大數運算的不易.

引例 在沒有計算器的幫助下，求下列各式的值：

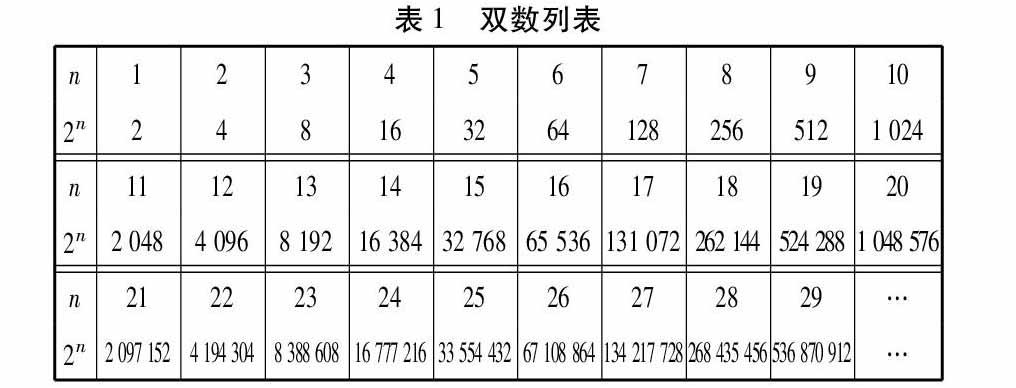
（二）雙數列表的引入[2]

（三）實例引入

教師：上述雙數列表中的特例都是設計好的，這些大數均為2的整數次冪.而在天文學家的實際計算過程中，遇到的數字都是有實際意義的天文數字，不可能剛巧都是2的整數次冪.華東師范大學的汪曉勤教授在《數學史與數學教育》中舉了一個實例——天文學家必會面臨計算299 792.458×31 536 000這一問題，因為它是光速與一年的秒數的乘積，也就是一個光年的大小[3].這樣的大數乘法運算如何巧妙地轉化為小數的加法運算呢？只要我們能夠找到a，b，使得2a=299 792.458，2b=31 536 000，就可以通過查找雙數列表的方法，簡便地進行計算.

（四）對數符號的誕生

面對上述光年計算的問題，教師提出疑問：若已知實數a>0，a≠1，且實數N>0，問使得ab=N成立的實數b是否存在？如果存在，是否唯一？

此處是本節課的重點之一.首先，面對計算光年這一實際問題，學生已經認識到尋找b值的必要性.其次，就是如何尋找b值，b值是否存在且唯一.對于指數函數f（x）=ax，其值域為一切正實數，因此，對任意的N>0，必定存在x0∈R，使得ax0=N，這便驗證了方程ax=N至少有一個解，而后利用指數函數f（x）=ax的單調性可知方程ax=N至多一個解.綜上可得ax=N恰有一個解，這個解便是b，即證明了使得ab=N成立的b值存在且唯一.

然后，教師便由拉丁文logarithm引入對數符號.

（五）對數的命名

教師向學生提出思考題：為何要將這樣的b稱為對數呢？對數難道表示“對的數”嗎？

沒有經歷上述對數概念引入過程的學生估計很難回答這個問題.而通過上半節課的引入，經歷過對數概念引入過程的學生能非常自然地回答出：對數即對應的數，通過雙數列表，我們可以將大數轉化為與其對應的小數.

（六）對數式與指數式的互化練習

（七）對數運算的引入及性質1的推導

教師幫助學生回顧前半節課的內容：在引例中我們能夠通過指數（小數）找到對應的冪（大數），現根據對數概念，我們也可以從真數（大數）出發，找到其對應的對數（小數）.

教師順勢改編雙數列表（表1），得到表2：

教師以指數的運算性質作為切入點，自然地引導學生過渡到對數的運算性質.對數有三大運算性質：如果a>0，a≠1，M>0，N>0，n∈R，那么有

（八）對數運算性質2、性質3的引入

對于對數的運算性質2、性質3的引入，筆者想出了兩種不同的設計方案，具體如下：

最終，筆者決定采用方案2.理由如下：

其一，方案1雖然很嚴謹，能夠培養學生由特殊到一般的思想方法，但是較為枯燥，對三大性質的生成與證明是一種機械重復的過程，而且十分耽誤時間，會導致后面教學時間不足.方案1看似是根據實例，由特殊到一般去找尋對數的運算性質，但實際上仍是教師強加思路給學生，學生完全是跟著教師在走，沒有發揮主觀能動性，并不符合本節課的教學理念——自然發生法.

其二，方案2邏輯線清晰有條理，教學的發生十分自然.教師負責搭建框架，其余完全由學生主導.方案2由例題引出對數運算性質3，既彌補了因時間不夠而導致的例題缺失、無暇訓練的不足，又在課堂中完美地展現了三大運算性質，實現了教學的完整性.

因此，無論是教學的自然發生，還是時間的把控，方案2都更勝一籌.

三、反思與總結

為達成本文第一部分所提出的三個目標，本節課的時間分配如下：

0～8分鐘：“課前引入”“雙數列表引入”“實例引入”.以HPM為主視角，采取數學史融入數學課堂的重構式設計，讓學生經歷煩瑣的大數運算，認識尋找對數的必要性.

8～15分鐘：“對數符號的誕生”“對數的命名”.回顧引例中大數與小數之間的關聯，根據已習得的指數函數值域與單調性的知識，引入對數概念，并簡要介紹對數的命名.

15～20分鐘：“對數式與指數式的互化練習”.通過簡單的指對數互化練習，引導學生主動發現：① 真數必須大于0;② loga1=0;③ logaa=1.

20～28分鐘：“對數運算的引入及性質1的推導”.通過引例，改編雙數列表，再通過特殊到一般的思想方法由結論發現對數的加法運算性質（性質1），前后呼應.

28～32分鐘：“對數運算性質2的引入”.根據加減法互為逆運算，由學生自主探究對數減法運算性質（性質2）并證明.

32～40分鐘：“對數運算性質3的引入”.給出例題，一來給學生時間鞏固知識，二來可以自然地引出運算性質3，一舉兩得.

將數學史融入數學教學能讓課堂變得生動有趣、激情澎湃，數學本體知識的教學則讓課堂變得嚴謹縝密、厚重如山.本節課在給出對數的定義之前，先提了一個問題：“若已知實數a>0，a≠1，且實數N>0，問使得ab=N成立的實數b是否存在？如果存在，是否唯一？”這是一個非問不可的問題，也是一個必須解決的問題.如果教師無視這個問題就直接給出對數的定義，那么對學生而言，對數的定義就是教師強加的，就算記住了這個定義，那也不過是無根浮萍而已.如果在圓滿地解決這個問題之后，教師再給出對數的定義，那么課堂將充滿思辨的火花，自然而然，行云流水，這個定義將在學生心中生根發芽，穩如磐石.

本節課結合對數的產生這一史實，設計了一次“穿越時空”的數學之旅，讓學生親身經歷了對數概念的產生與發展過程，讓學生沐浴在先哲的思想光輝中;同時，本節課將數學史教學與數學本體知識教學巧妙融合起來，使學生在思維活躍、邏輯清晰的本體知識教學中收獲真知.

如何在一節數學教學課中，為數學史、數學本體知識找到一個最佳的平衡點，并將兩者熔為一爐、水乳交融？這是值得一線教師全身心投入其中、不懈探索與實踐的新問題.

【參考文獻】

[1]上海市中小學（幼兒園）課程改革委員會.高級中學教材·數學（高中一年級第二學期試用本）[M].上海：上海教育出版社，2015.

[2]吳晨昊.HPM視角下的“對數概念及其運算”的教學[J].數學教學，2016（12）：37-41.

[3]汪曉勤.HPM：數學史與數學教育[M].上海：科學出版社，2017：451-546.