究竟誰的面積更大？

毛玉暄

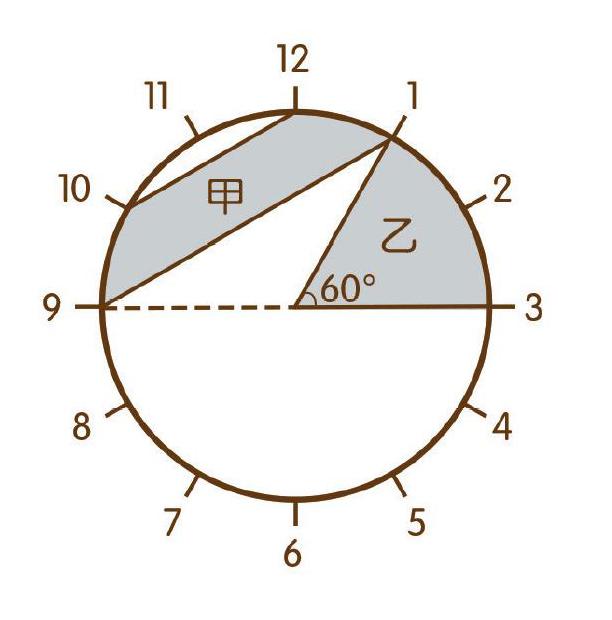
最近，李老師帶著我們一起回顧和復習平面圖形面積的相關知識。我突然發現，我們現在學到的、能用公式直接計算面積的圖形只有正方形、長方形、平行四邊形、三角形、梯形和圓形等規則的幾何圖形。其他的幾何圖形，尤其是不規則的圖形，或者是所給已知條件較少的圖形，都不能套用公式來計算面積，而是需要將其“轉化”成我們熟悉的圖形。

題目中的兩個陰影部分既不是規則的梯形，也不是規則的三角形。但我清楚，計算不規則圖形的面積應該試著將其回歸到計算規則圖形的面積上。讓我著急的是題目中的已知條件太少，這個比較麻煩。

題目只讓我們比較兩個陰影部分面積的大小，不需要計算結果。于是，我就可以從兩個陰影部分與整個圓的關系入手，進行判斷。

經過一番觀察，我發現：乙是一個扇形，其圓心角是360°÷12×2=60°，所以它的面積是整個圓的面積的1

6。這樣一來，只要判定甲的面積占整個圓的面積的幾分之幾即可。

我想到了利用兩個規則圖形的面積差來表示甲的面積。甲上方有一塊空白的部分（弓形），是不是可以將乙切割下一部分補過去呢？補過去之后，乙的剩余部分就是一個規則的三角形了。

我還發現乙的剩余部分（三角形）和甲下方的空白部分（三角形）都是三角形，并且兩個三角形的底都為圓的半徑，還共用一條高，說明它們的面積相等。這樣，我就可以將乙的剩余部分（三角形）轉化為甲下方的空白部分（三角形）。

經過這樣的操作之后，陰影部分甲與乙的面積合在一起，正好是一個大的扇形的面積。

通過此時的鐘面可以看出，這個扇形的圓心角是120°，則它的面積是圓的面積的1

3 。所以，甲的面積等于該扇形的面積減去乙的面積，也就是圓的面積的1

6。所以，甲和乙的面積一樣大。

這下，想必大家對求解圖形面積的問題有了更好的了解。希望大家在以后的學習中，能善于使用割補法來求解或者比較不規則圖形的面積。

指導老師? 李小強