崎嶇山地環境履帶機器人降維變系數控制方法研究

劉 路 楊 冰 韋 東 宋 宇 陳黎卿 孫 燕,3

(1.安徽農業大學工學院， 合肥 230036； 2.安徽省智能農機裝備工程實驗室， 合肥 230036；3.安徽省工業節電與電能質量控制協同創新中心， 合肥 230601)

0 引言

近年來，小型履帶機器人廣泛應用于田間作業中，由于田間路面崎嶇不平[1-3]，易造成航向偏差增大。因此，車身側傾、俯仰對小型履帶式機器人的影響成為農田環境下農業導航控制領域不可忽視的因素[4-8]。為解決路面崎嶇不平對小型履帶機器人的影響問題，國內外諸多學者多采用二維平面滑模控制(SMC)作為位姿控制系統[9-14]，解決了二維平整路面路徑跟蹤的問題。機器人在三維崎嶇路面上的姿態控制誤差與機器人行駛過程中的姿態變化有關，需要探索合適的姿態檢測及控制修正方法，以提升機器人實時控制精度[15-20]。

針對上述問題，本文以小型履帶機器人作為研究對象，設計一種基于降維變系數的滑模控制系統，該系統采用慣導傳感器與RTK北斗定位系統，實時檢測車身位姿信息，微控制器將理想位姿信息作為降維變系數系統的控制輸入，實時匹配兩側履帶運行速度，以達到在崎嶇路面修正車身航向、提高行駛穩定性的目的。

1 履帶機器人系統組成與原理

1.1 履帶機器人結構及主要參數

為了實現行距800 mm的壟間精確導航和精準控制，履帶機器人的整機結構如圖1所示，主要功能包括機器人運行過程中通信、電機驅動和車身控制，相關技術參數如表1所示。

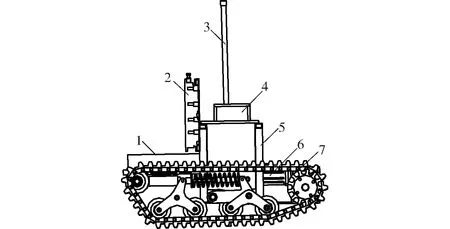
圖1 小型履帶機器人整機結構簡圖

表1 小型履帶植保機器人主要技術參數

1.2 降維變系數底盤建模方法

機器人在路面上行駛時，地面坐標系為XOY，機器人的局部坐標系xoy中令機器人質心為原點，局部坐標系相對于地面坐標系的位姿可表示為T1，如圖2所示。

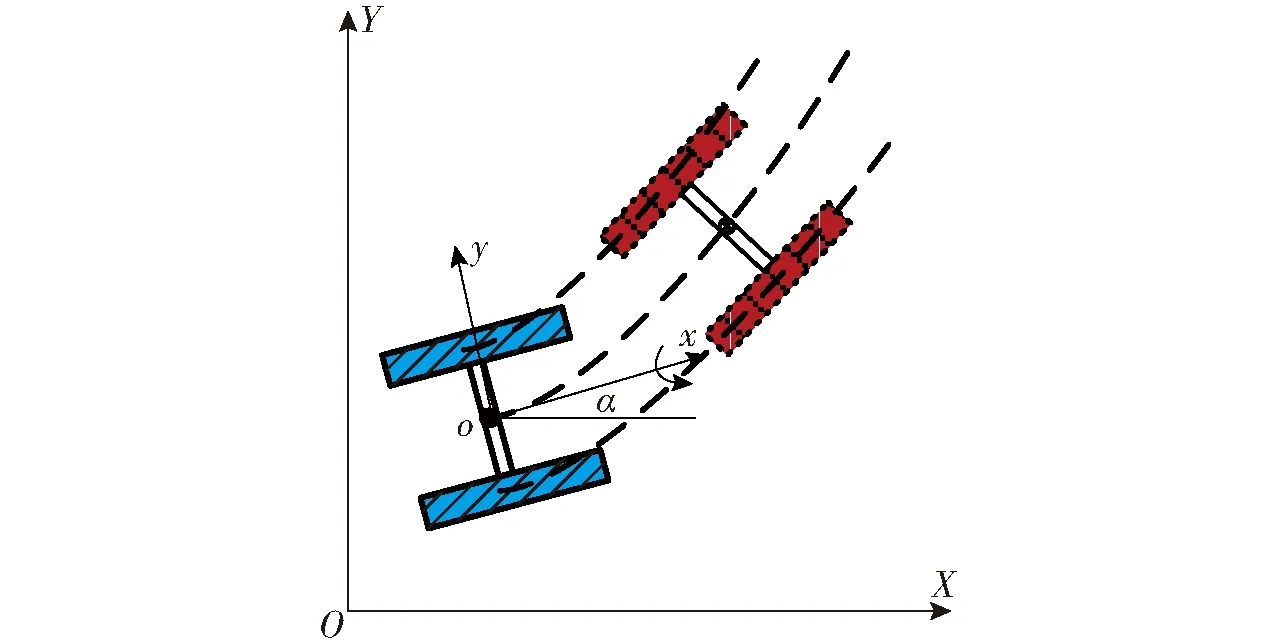
圖2 二維平整路面運動簡圖

圖2機器人的二維運動學方程與誤差方程為

T1(x,y,α)=N1(α)Q1(v,ω)

(1)

K1(xe,ye,αe)=R1(α)A1(Δ)

(2)

式中T1(x,y,α)——二維機器人位姿

x、y——機器人運動時，x、y軸方向移動距離

α——機器人運動時，局部坐標系x軸與地面坐標系X軸間的夾角，亦稱為偏航角

N1(α)——二維實際和理想位姿坐標系轉換矩陣

Q1(v,ω)——二維機器人線速度、角速度矩陣

v——線速度

ω——角速度

K1(xe,ye,αe)——二維機器人位姿誤差

xe、ye——x、y方向誤差

αe——偏航角誤差

R1(α)——二維實際位姿和理想位姿誤差坐標系轉換矩陣

A1(Δ)——二維實際位姿與理想位姿誤差矩陣

Δ——二維實際位姿與理想位姿誤差

機器人在非平整路面運動時，出現隨機的姿態側向或俯仰變化，二維運動模型的路徑跟蹤會有較大跟蹤誤差。為保證機器人的路徑跟蹤精度，需要對車身上述姿態變化導致的誤差進行補償以實現姿態的修正與位置糾偏。

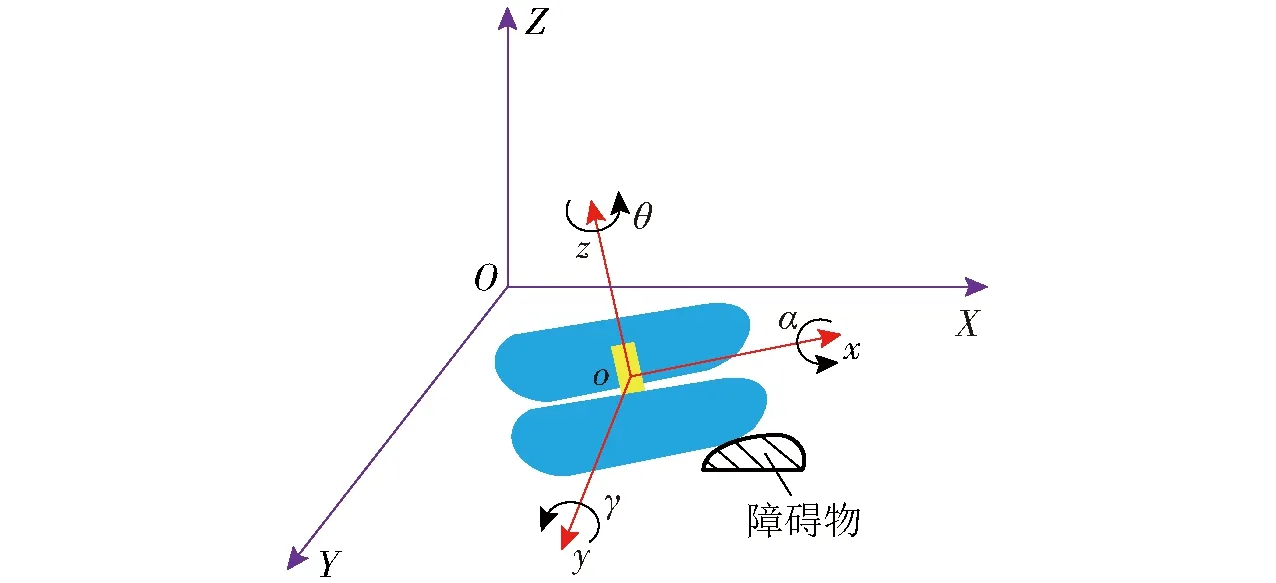
圖3 三維崎嶇路面運動簡圖

三維運動模型與二維運動模型相比，增添垂直于地平面方向的Z軸，如圖3所示。降維模型利用機器人實際三維空間位姿與理想三維空間旋轉映射關系，使機器人運動過程中通過對映射后的輪距、航向的投影參數修正將控制模型始終保持在地面坐標系XOY平面內，從而去除控制模型中z軸方向變量，θ、γ為機器人運動時自身所處的局部坐標系中z、y軸分別與地面坐標系中Z、Y軸的夾角，即橫滾角與俯仰角。其自身所處的局部坐標系原點相對于地面坐標系的位姿表示為(x,y,z,α,θ,γ)，因此其降維變系數模型、運動學方程與誤差方程為

U(xe,ye,αe)=f(θ,γ)

(3)

T2(x+xe,y+ye,α+αe)=N1(α)f(θ,γ)Q1(v,ω)

(4)

K2(xe,ye,αe)=R2(α)f(θ,γ)A2(Δ)

(5)

式中U(xe,ye,αe)——投影參數修正函數

f(θ,γ)——空間旋轉映射函數

T2(x+xe,y+ye,α+αe)——三維機器人位姿

K2(xe,ye,αe)——三維車身位姿誤差

R2(α)——三維實際位姿和理想位姿誤差坐標系轉換矩陣

A2(Δ)——三維實際位姿與理想位姿誤差矩陣

上述降維變系數中，將圖3所示三維狀態下機器人位姿通過映射投影的方法獲得理想位姿。在映射投影過程中，姿態發生變化產生二維平面位姿誤差，因此，采用投影參數修正函數U(xe,ye,αe)通過映射函數f(θ,γ)對產生的誤差進行補償，進而消除z軸方向與θ、γ波動對跟蹤精度的影響。三維運動學模型T2在映射函數f(θ,γ)的補償下進行二維控制，最終達到降維控制的目的。

2 降維變系數控制方法

在降維運動學幾何模型基礎上，設計基于降維變系數的位置控制外環、偏航角控制內環、滿足機器人運動約束條件的控制策略，實現機器人對于位置、姿態的精確控制，同時實現在崎嶇非平整路面上平穩行駛的功能。

2.1 糾偏系統工作原理

本文所研究的雙輪差速轉向履帶機器人，通過控制兩驅動輪的轉速對車身姿態與理想軌跡進行調節與跟蹤。機器人實際位置信息作為控制輸入，其線速度與角速度作為控制輸出，通過理想路徑與實際路徑的誤差反饋，由糾偏控制系統消除理想位置與實際位置的誤差，最終實現路徑跟蹤。

上述閉環系統屬于雙環滑模控制系統，其中姿態控制系統為內環，位置控制系統為外環。位姿信息在控制律p1、p2、p3和p4的控制下通過降維變系數模型傳遞給內外環控制，完成對線速度、角速度的控制，最終達到路徑跟蹤的目的。其控制流程圖如圖4所示。

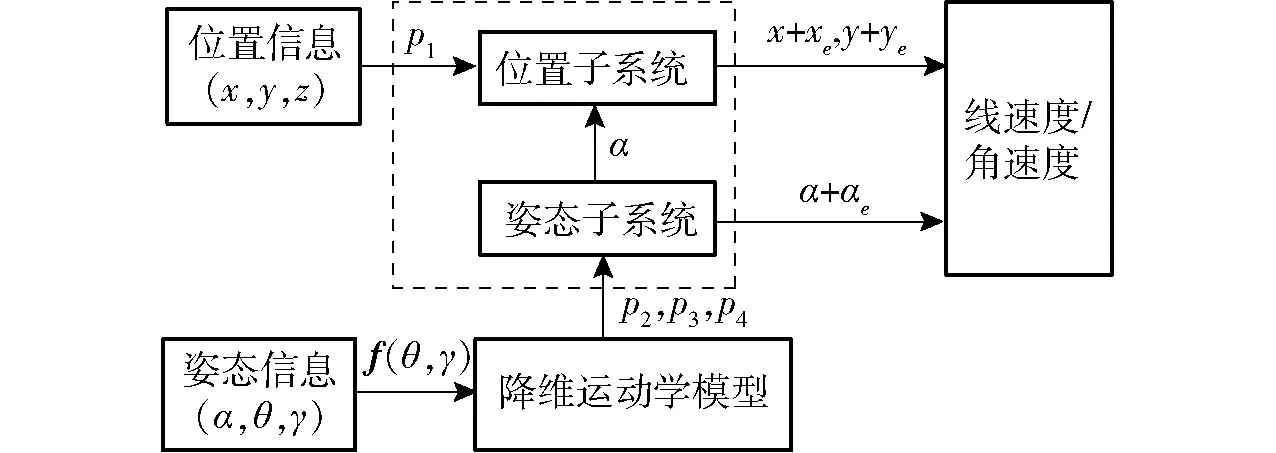
圖4 降維變系數控制系統流程圖

2.2 降維變系數控制系統組成

降維變系數控制系統由STM32F407ZGT6型微處理器、MTI-G-710型慣導傳感器、ZM-6615型直流無刷電機驅動器、直流無刷電機等組成，如圖5所示。其中，慣導傳感器提供姿態信息，RTK北斗定位系統提供位置信息，上位機根據控制模型輸出控制變量，輸出的控制變量通過運動控制器將線速度、角速度信息轉換成左右履帶輪電機轉速，最終兩輪差速運動實現路徑跟蹤。

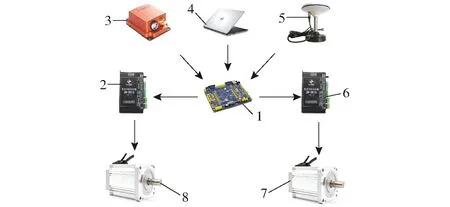
圖5 控制系統組成與結構

2.3 降維變系數控制系統設計

2.3.1位置外環控制律設計

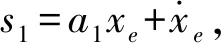
(6)

上述位置控制系統中p1在x方向的子系統控制律為p1x

式中q1——波動量λ1、a1、η1——控制參數

由此可以得到

(7)

若系統趨于穩定，則x方向線速度為

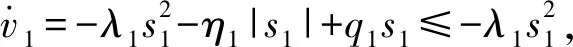
同理，針對y控制系統，設計控制律為

(8)

式中λ2、a2、η2——控制參數

p1y——在y方向的位置子系統控制律

s2——在y方向的滑模函數

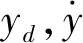
2.3.2偏航角內環控制律設計

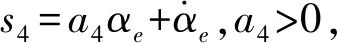
(9)

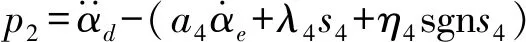
(λ4>0,η4>0)

式中q4——波動量

得到

若系統趨于穩定，則需要x方向線速度為

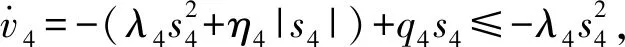
同理，針對θ、γ控制系統，其控制律為

(10)

(11)

從而實現s5、s6指數收斂，θ、γ收斂于理想姿態θd、γd。最終實現履帶機器人對理想姿態曲線的角度跟蹤。

由于獨立的外環控制在位置跟蹤過程中易受到姿態波動的影響，產生跟蹤誤差大、穩定性差的情況，因此引入偏航角內環控制，通過內環收斂速度大于外環收斂速度的方法，確保整個降維變系數控制系統的穩定。

3 仿真試驗

為了驗證降維變系數控制方法可在二維路面上進行精確跟蹤，以雙輪差速轉向模型作為仿真對象，在Matlab/Simulink環境下進行二維平整路面路徑跟蹤仿真試驗。二維路徑追蹤試驗中，初始位置與姿態設為(0,0,0,0,0,0)，設置理想路徑為

(12)

表2 二維仿真相關參數

在此平面路徑下，進行二維路徑仿真跟蹤時，由于不存在z軸數據，故而僅需仿真x、y軸誤差與追蹤α即可。仿真結果如圖6所示。

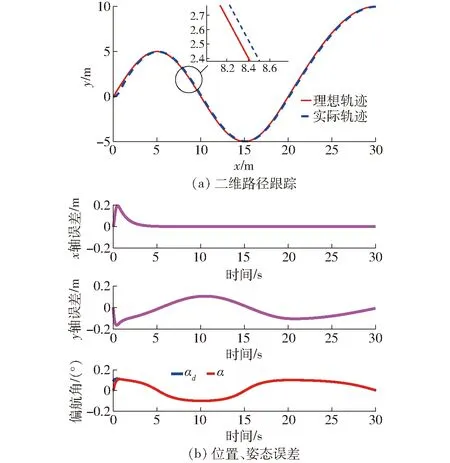
圖6 二維路徑跟蹤仿真結果

二維路徑仿真結果表明，二維平整路面路徑跟蹤過程中，x軸誤差在初始的0～2 s內便逐漸減少至0。y軸誤差始終控制在±0.2 m之間，偏航角最初的1 s內精確跟蹤了理想角度。

為了驗證降維變系數控制方法在三維崎嶇路面跟蹤的精確性，進行三維路徑跟蹤仿真試驗，具體仿真參數如表3所示。

考慮到路面起伏，取理想路徑函數為初始位置與姿態設為(0,0,0,0,0,0)。

(13)

表3 三維仿真相關參數

三維路徑跟蹤仿真結果如圖7所示。圖7a表明，履帶機器人可精確跟蹤二維平整路面理想軌跡，結合圖7b歐拉角追蹤，表明機器人在跟蹤上理想偏航角αd后，便無較大范圍的波動。在三維路面的頂點或坑底等角度瞬間變化時，降維變系數控制方法能在1 s內快速地跟蹤理想的偏航角、滾動角和俯仰角。

結合圖7a與圖7c可以看出，由于起始點位置設為原點，故而在0～6 s的初始階段x、y、z軸存在較大的誤差。6 s后，隨著時間的增加，三軸位置誤差逐漸減小，直至誤差在±0.1 m內波動。

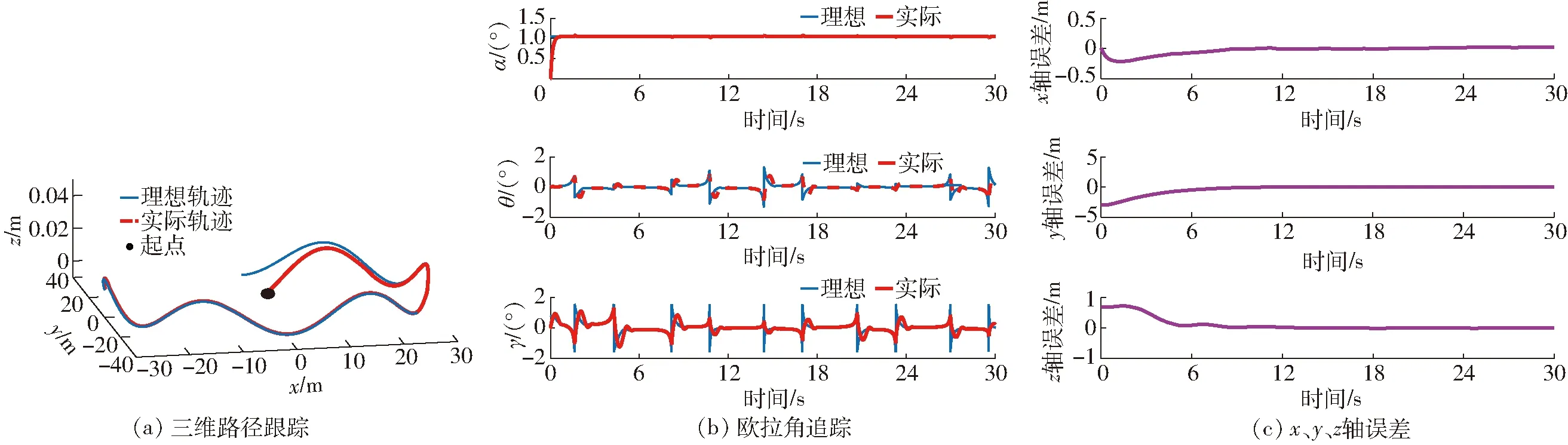
圖7 三維路徑跟蹤仿真結果

二維平整路面與三維崎嶇路面相比，二維平整路面仿真時將a4、a5、a6、λ4、λ5、λ6設置為0，僅改變剩余的控制參數，記錄機器人的路徑跟蹤結果，仿真結果表明二維路面和三維路面誤差均滿足實際需要。

4 降維變系數控制試驗

為了驗證本文方法的可行性，以安徽農業大學安徽省智能農機裝備工程實驗室研制的履帶機器人作為試驗平臺，試驗環境為非硬化崎嶇路面和硬化平整路面兩種，設計車速為1.5 m/s。對理想的二維平整路面與三維崎嶇路面進行路徑跟蹤田間試驗，如圖8所示。

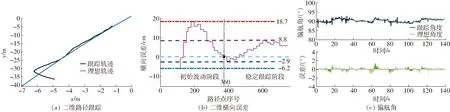
圖9 二維平整路面路徑跟蹤試驗結果

圖8 田間試驗

二維平整路面試驗結果如圖9所示。圖9a中，在理想軌跡與實際軌跡第2次相交時可認為機器人由初始波動階段進入穩定跟蹤階段。如圖9b所示，在平面上跟蹤時，其初始波動階段的橫向誤差在-6.2～18.7 cm之間，在路徑點為360時，機器人處于穩定跟蹤，其誤差在-2.9～8.8 cm內波動。偏航角跟蹤如圖9c所示，其跟蹤誤差在±2°之間，符合控制要求。

崎嶇路面試驗結果如圖10與圖11所示。其中，圖10a為本文崎嶇路面下行駛軌跡與路譜圖；圖10b與圖10d分別為圖10a在xy平面與z軸方向投影的跟蹤圖。如圖10b與圖10d所示，本文所提出的降維變系數控制系統能夠較好地追蹤目標路徑；在實際軌跡與理想軌跡第4次相交時，機器人由初始波動階段進入穩定跟蹤階段，其跟蹤誤差如圖10c所示，橫向誤差在初始波動階段的誤差范圍為-23.6～52.7 cm，在路徑點序號為381時，由初始波動階段進入穩定跟蹤階段，機器人在穩定跟蹤階段的誤差范圍為-14.3～21.5 cm，都處于合理的控制范圍內。俯仰角、橫滾角與偏航角分別如圖11所示，其控制波動皆在±5°以內。

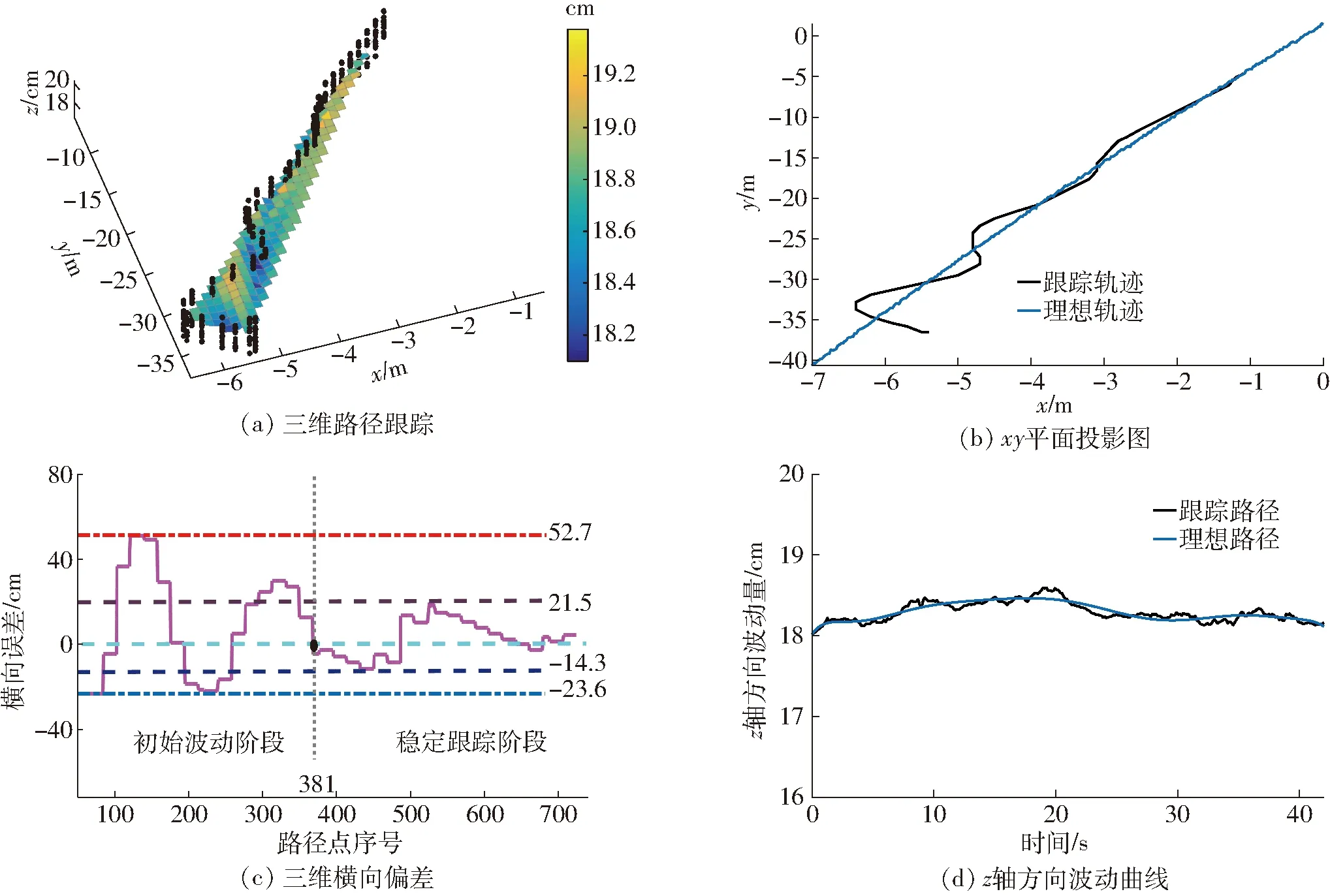
圖10 三維崎嶇路面位置跟蹤試驗結果

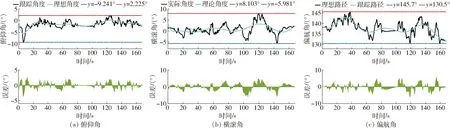
圖11 三維崎嶇路面角度跟蹤試驗結果

5 結論

(1)采用數學建模方法建立了三維運動學模型與誤差方程，基于此設計了一種崎嶇山地環境下的履帶機器人降維變系數控制系統。

(2)Matlab環境下的仿真結果表明，所提出的控制方法能夠對履帶機器人進行有效的控制，并且能夠對理想路徑進行有效的跟蹤。其二維平整路面仿真結果表明，x軸誤差逐漸減少為0，y軸誤差控制在±0.2 m范圍內，航偏角在1 s內完成跟蹤理想角度；三維崎嶇路面仿真結果表明，三軸姿態角在1 s內完成對理想姿態角的跟蹤，同時三軸誤差都控制在±0.1 m內。因此，在仿真階段能夠滿足履帶機器人保持在800 mm寬作物行內的行駛要求。

(3)履帶機器人在二維平整路面上進行路徑跟蹤時，其橫向誤差在初始波動階段波動范圍在-6.2～18.7 cm之間，機器人處于穩定跟蹤時，其誤差在-2.9～8.8 cm內波動，姿態角在±2°范圍內波動。在三維崎嶇路面上，采用降維變系數控制方法能夠對理想路徑進行有效跟蹤，機器人橫向誤差在初始波動階段范圍為-23.6～52.7 cm，在穩定跟蹤階段范圍為-14.3～21.5 cm，姿態角控制在±5°范圍內。說明履帶機器人能夠保持在800 mm寬作物行內的正常行駛。