GeoGebra軟件在高中數學教學中的探究性應用

張勇

摘要：隨著現代信息技術的發展，計算機技術與其它學科的整合也日趨完善，GeoGebra是一款免費的動態數學軟件，它整合了代數、幾何與微積分，是輔助數學教學的優秀軟件，尤其是對于高中數學教學GeoGebra具有一些獨特的優勢，下面就此談一談自己的一些實踐與認識。

關鍵詞：GeoGebra;數形結合;動態演示

1? GeoGebra軟件的特點

GeoGebra是2002年由美國佛羅里達州亞特蘭大學的Markus Hohenwarter教授所設計的一款結合幾何、代數和微積分的免費動態數學軟件。以直線，向量，曲線，函數等為基本元素，提供了方便的動態演示，顯示和探索軌跡的生成過程，以“動態”為特色，展示代數，幾何圖形內在關系的環境，使原本抽象，枯燥的內容變得具體、生動、形象，充分展示了數學教學的美。該軟件不僅有電腦版本的安裝程序，還有支持移動終端設備的APP程序，極大的擴大了它的應用范圍。

2? 基于GeoGebra的數學應用案例

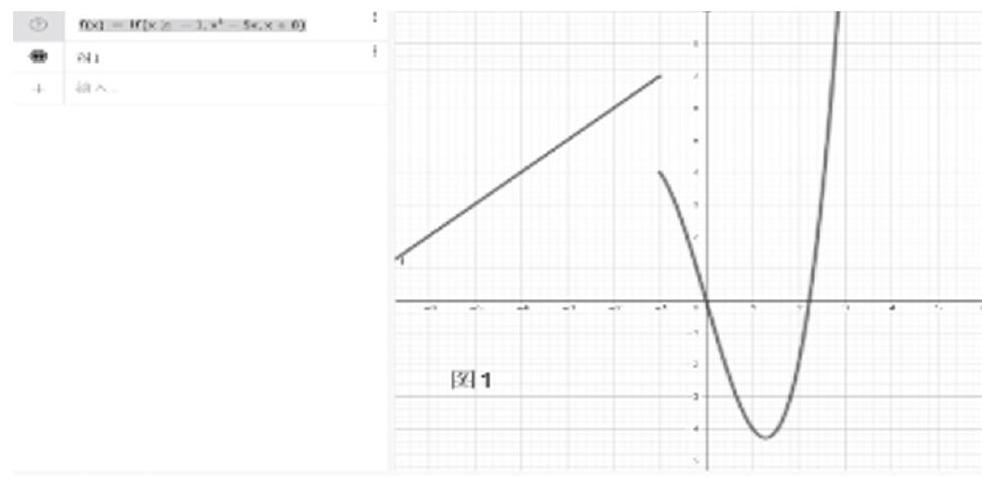
案例1 繪制分段函數的圖像

借助函數圖像可以非常直觀地幫助學生理解函數性質，畫出函數圖像成為函數教學中突破難點的一種有效手段。

例1：已知分段函數y=x3-5x （x≥-1）;y=x+8 （x<-1），我們只需要在命令框輸入“if（x≥-1， x3-5x，x +8）”，便可得到圖1的結果。

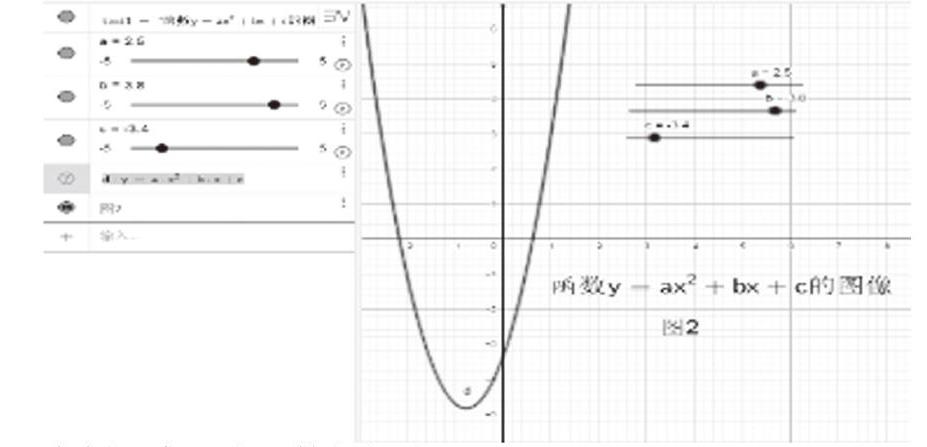
案例2 二次函數的動態觀察

二次函數的參數對函數圖像的影響是難點，傳統教學方法很難突破教學難點，但是運用GeoGebra軟件，能夠形象動態地演示三個參數的變化引起函數圖像的變化，能夠加深學生的印象，從而有效突破教學難點。

例2：以y=ax2+bx+c函數的圖像為例，探究二次函數的三個參數的變化對函數圖像的影響。如圖2，分別建立三個滑塊a、b、c，輸入函數，繪制函數圖像。拖動滑塊，可以實時顯示函數圖像的變化，從而能夠讓學生觀察各個參數的變化引起二次函數圖像的變化規律。

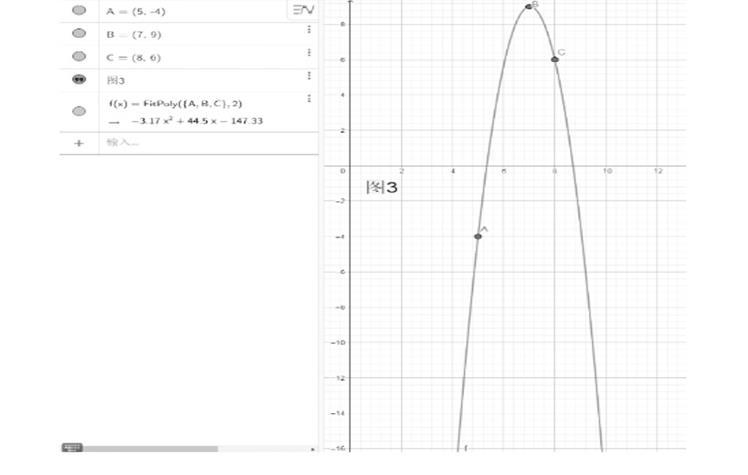
案例3 求二次函數解析式

學生在求二次函數解析式，很苦惱的一件事情就是計算，枯燥乏味的練習成為學生學習數學的攔路虎，GeoGebra作為函數學習的神兵利器，它強大的計算功能很好地滿足了學生在二次函數計算方面的需要。

例3：如果一個二次函數經過A（5，-4）、B（7，9）、C（8，6）三點，試求該二次函數的解析式。

如圖3，在輸入區輸入A=（5，-4）回車，B=（7，9）回車，C=（8，6）回車，在繪圖區出現A、B、C三點，緊接著在輸入區輸入“fitpoly（A，B，C，}，2）”回車，會自動計算出函數解析式。

案例4 求函數圖像的交點

例4：已知函數y=x2與y=5x+4，利用函數圖像求交點。

如圖4，在輸入區輸入f（x）=x2，g（x）=5x+4緊接著輸入交點命令Intersect（f，g）回車，GeoGebra會自動計算出兩個交點A，B的坐標。

案例5 在函數極限教學中的應用

例5：計算極限 。

這是微積分教學中一個比較重要的極限，理論計算比較復雜，而使用GeoGebra軟件演示給學生，則能收到事半功倍的效果。

步驟：（1）設置變量X滑桿，其增量可設置為0.0001;（2）定義點A=（x，f（x）），其中;

（3）拉動滑桿并設置點A軌跡即可得圖5;在作圖區可以看到點A的軌跡，在代數區可以看點A坐標的變化趨勢，由圖5可直觀得到所求極限的值為0。

3? 結束語

GeoGebra為“數形結合”創造了一條便捷的通道， 它不僅對幾何模型的繪制提供信息， 同時， 可以解決學生難以繪制的圖形， 而且提供了圖形“變換”的動感，使學生從畫面中去尋求到問題解決的方法和依據， 并從畫面中去認清問題的本質。彌補了傳統教學所缺乏的“以形助數”，“用數解形”，從而實現了真正的動態演示。