數學名題：為學生種下一顆數學研究的種子

○蔣守成

主題拓展教學基于對教材內容的系統把握與對學生學習經驗、生活經驗的準確理解兩個層面，以主題為核心建設主題課程資源，為學生提供只有在數學學習中才會經歷和體驗并建立起來的獨特的思維方式。

數學名題中蘊含了深厚的數學史，隱藏了豐富的數學思想方法，介紹了數學家發現問題和研究問題的歷程，具有典型性和廣泛的影響力。因此，我們以數學名題為主題，為學生種下一顆數學研究的種子，來激活凝固的書本知識，使知識恢復到鮮活的狀態，實現書本知識與學生發現問題、解決問題、形成知識過程相關聯，實現書本知識與學生的生活世界和經驗世界相關聯，豐富和拓展數學學科的育人資源，全面發展學生的思維。

一、解讀教材，拓展數學名題的育人價值

數學名題是指在數學發展歷史長河中形成，并對數學發展、數學應用和數學教學等方面起過或仍起著重要作用的數學問題。

例如：楊輝三角、哥尼斯堡七橋問題、哥德巴赫猜想、雞兔同籠……這些著名的數學問題是數學家經過幾百年甚至上千年的不斷探索與思考的智慧結晶，在數學史上產生較大影響，對數學發展有一定的推動作用。不同版本的小學數學教材中也都編排了一些數學名題，讓學生經歷像數學家一樣研究的過程，感受新概念的誕生，體悟新方法的形成，感悟深厚的數學文化，體會數學在人類發展史中的作用。

數學名題蘊含著重要的數學思想方法，是提升學生數學素養的有效載體。例如，“物不知其數”蘊含了同余的思想方法，“七橋問題”不僅是抽象的典型實例，同時也蘊含轉化的思想方法。因此，我們應對數學名題的素養目標和教學價值進行定位，為課程資源開發和課堂教學提供幫助。（下表是部分數學名題的素養目標和教學價值定位。）

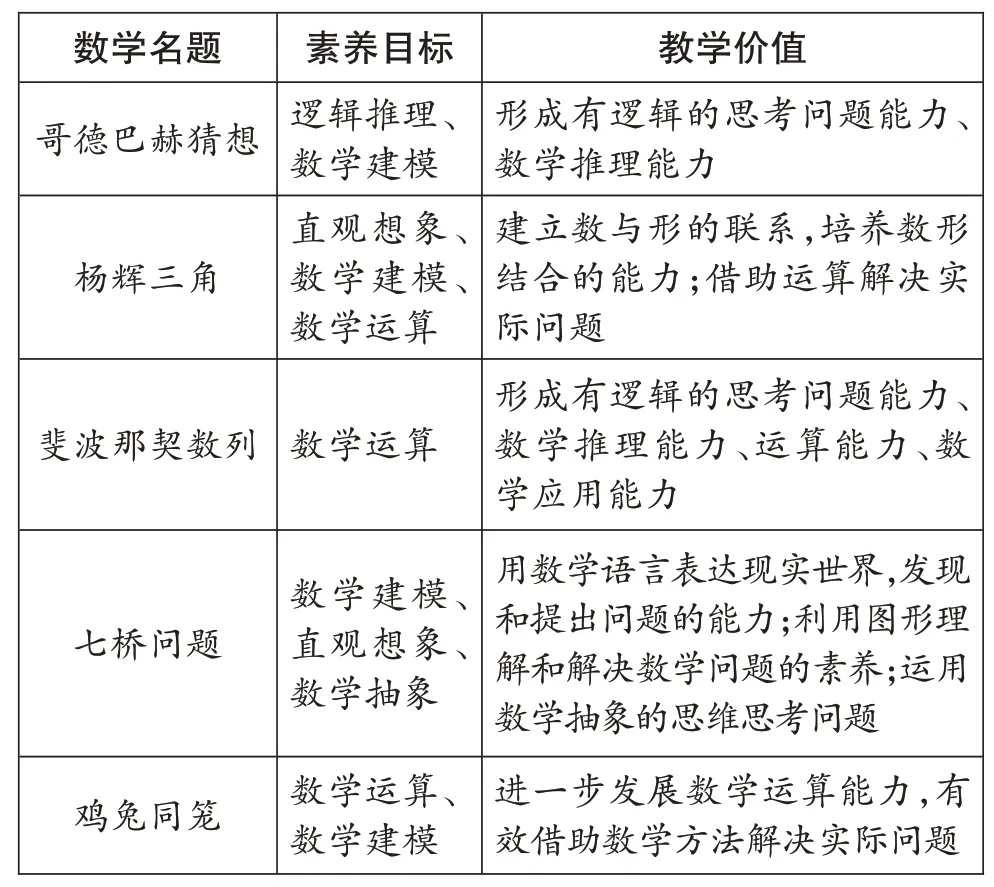
數學名題哥德巴赫猜想楊輝三角素養目標邏輯推理、數學建模直觀想象、數學建模、數學運算斐波那契數列數學運算七橋問題雞兔同籠數學建模、直觀想象、數學抽象數學運算、數學建模教學價值形成有邏輯的思考問題能力、數學推理能力建立數與形的聯系，培養數形結合的能力；借助運算解決實際問題形成有邏輯的思考問題能力、數學推理能力、運算能力、數學應用能力用數學語言表達現實世界，發現和提出問題的能力；利用圖形理解和解決數學問題的素養；運用數學抽象的思維思考問題進一步發展數學運算能力，有效借助數學方法解決實際問題

其實能在小學數學課堂上滲透的數學名題還有很多，比如“省刻度尺”“和尚分饅頭”“棋盤上的麥粒”“李白喝酒”“田忌賽馬”“四色猜想”“冰雹猜想”“孿生素數猜想”……我們進行數學名題的主題教學研究，并不是要求學生做高深的數學研究，只是為學生創設一個可以像數學家那樣“想”的空間，讓學生經歷和數學家一樣的研究歷程，感受真理探索的艱辛，幫助他們形成不唯書、不唯師、不唯上的批判性思維，形成獨立思考、自由探索的數學品質，拓展數學學科的育人價值，全面提升學生的數學素養。

二、整合教學，放大數學名題的教學價值

學會思維是學生思維發展的必由路徑，“學會”強調的是過程，而非結果，每個人都要學會思維，但學會的標準是多元的，學會的路徑是靈活的。我們依據學生的年齡特點和認知水平，基于教材內容，精心選擇開發了52 個小學生能懂的數學名題，為學會思維提供過程支架，從中年級的數學閱讀和高年級的名題研究兩個路徑來放大數學名題的教學價值。

（一）數學名題主題閱讀。

我們在中年級進行數學名題閱讀欣賞，讓學生感受名題中的數學思想和方法，吸取名題中的數學文化和數學精神，提升對數學學習的興趣，感受數學的魅力。例如：我們將數學名題改編成數學童話，供三四年級學生進行閱讀。

時空穿梭解名題系列之《和尚分饅頭》

點點和芳芳都是數學愛好者，她們很想了解古代人是如何學習數學的。一次偶然的機會，她們得到了外星人留在地球上的時空穿梭機，真的實現了時空穿梭，眨眼間便回到了明代。

她們來到一座寺廟前，點點說：“我們進去玩玩吧！”可是當她們來到寺廟門口便被幾個和尚攔住了：“寺廟只接待香客，不接待游客！”這時一位老伯說：“小朋友，如果你們能回答上我的問題，我就分幾炷香給你們。”點點說：“行，什么問題？”老伯說：“一百饅頭一百僧，大僧三個更無爭，小僧三人分一個，大小和尚各幾丁？”點點聽得有些摸不著頭腦，便問芳芳：“這是什么意思啊？”芳芳說：“這是明代《算法統宗》中的問題，意思是說一百個和尚吃一百個饅頭，大和尚每人吃三個，小和尚每三人吃一個，大小和尚各有多少人？”

點點說：“原來是這么回事，這題我會解。把1個大和尚與3個小和尚看成一組，那每組得分4個饅頭，100÷4=25（組），說明有25 個大和尚、75 個小和尚。”

老伯驚嘆地問道：“小朋友好聰明，你叫什么名字？”點點也不客氣地問道：“你叫什么名字啊？”老伯笑道：“我叫程大位。”芳芳吃驚地說：“點點，他就是明代大數學家程大位，《算法統宗》就是他寫的！”點點一聽愣住了，老伯笑道：“我們現在就去燒香吧！”

通過數學閱讀把抽象、枯燥的數學問題加工成有趣且適合閱讀思考的學習材料，對學生進行數學思想、數學文化的滲透，將數學內在的理性精神以一種可以觸摸、可以表達、可以分享的方式告訴他們，讓他們去感悟，去體驗，去傳承。

（二）數學名題研究。

我們在高年級進行數學名題系列研究，從著名的數學問題“哥德巴赫猜想”“四色猜想”“冰雹猜想”“孿生素數猜想”“省刻度尺”“雪花曲線”“楊輝三角”等出發，化復雜為簡單，化深奧為淺顯，讓學生在學習過程中像數學家一樣去工作、思考和交流，培養數學學習的品質，讓學生的思維生長在研究過程中可見。

例如，我們以世界三大猜想之一的“四色猜想”為研究主題，讓學生充分經歷觀察、實驗、猜想、驗證的過程，體悟推理和模型思想。研究過程分三個板塊：

板塊一：引導學生自己提出猜想。

1.解決問題，引發猜想。呈現江蘇省地圖提出問題：從地圖上我們可以看出江蘇省由13 個城市組成。如果要把江蘇地圖涂上顏色，并且相鄰兩個城市要涂不同的顏色來區分。想一想，可以用幾種顏色？

學生回答有13種、12種、11種等等，答案不一致，但都能夠區分。

小結：看來按這樣的要求來涂色，方法可不止一種。那么到底最少需要幾種顏色就足以保證相鄰的兩個城市顏色不同了呢？

2.動手操作，探尋結論。按要求給下面3 個圖形涂上顏色，涂完后說明理由。

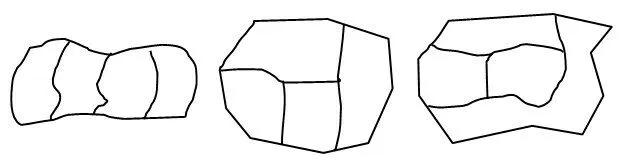
（1）每個圖形中相鄰的兩塊顏色不同。

（2）用的顏色要最少。

學生匯報后，教師追問：剛才我們研究的這3個圖形都被分成了4塊，為什么只有第3個圖需要4種顏色，而前2個圖不需要4種顏色呢？

同桌交流后分享：因為第三個圖中的每一塊都和其他三塊相鄰，而前2個圖形中并沒有這樣。

3.繼續探索，提出猜想。用你喜歡的方式把下面的圖形任意分成5 塊、6 塊、7 塊，按剛才的要求涂色，你能發現涂色的規律嗎？

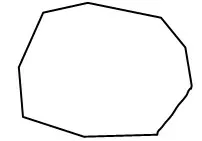
學生分享比較發現：把一個圖形任意分成4塊、5 塊、6 塊或7 塊，只要用4 種顏色來涂色，就足以保證相鄰的2 塊顏色不同。也有學生大膽地提出：把一個平面圖形分成若干塊，只要用4 種顏色涂色，就足以保證相鄰的兩塊顏色不同。這也就是著名的世界三大猜想之一：四色猜想。

板塊二：介紹“四色猜想”的發現和提出的過程。

1852 年，一位名叫葛斯瑞的英國繪圖員發現了一種有趣的現象：在每幅地圖上只要用4 種顏色來著色，就足以把有公共邊界的國家（或地區）分開，即把相鄰的國家（或地區）涂上不同的顏色。如果用數學語言來表示四色猜想就是：將一個平面圖形任意分為大于或等于4 個的不重疊區域，只要用1、2、3、4 四個數字來標記每個區域，就可以保證相鄰的兩個區域不會出現相同的數字。由此可以告訴學生：數學猜想不一定要數學家提出來，我們每個人都可以提出數學猜想，然后進行驗證猜想是否正確，這是一種很好的數學思考方法。

板塊三：自己驗證四色猜想，感受猜想的奇妙。

提問：讓你來證明四色猜想，你會怎么做？（舉例）

驗證：學生借助研究單上的地圖（江蘇地圖、北京地圖、寧夏地圖），用數字表示顏色的方法來驗證，發現都是4種。

追問：我們用了3 幅地圖驗證了四色猜想，你覺得這樣的證明夠不夠？這樣的例子還有很多，那科學家們又是怎樣來證明四色猜想呢？我們一起來了解一下。介紹數學家證明四色猜想的歷程，指出1976年9月，美國數學家阿佩爾和哈肯教授，用計算機做了100 億次的判斷后，最終完成了四色猜想的證明。

其實很多猜想就像“四色猜想”一樣來自我們的日常生活，例如“冰雹猜想”就是來自70 年代美國大學里風靡的數學游戲。當我們經常用數學的眼光去觀察日常的學習和生活時，也許下一個提出著名數學猜想的人就會是你！

數學名題的研究不僅使數學教學變得有意思，也讓數學教學變得更有意義，讓學生不僅僅停留在“知道”層面，更能夠促進學生把問題想得更清晰、更全面、更深刻、更合理，能夠體會人類認識世界、數學化地刻畫世界的過程，體悟到數學自身的魅力。