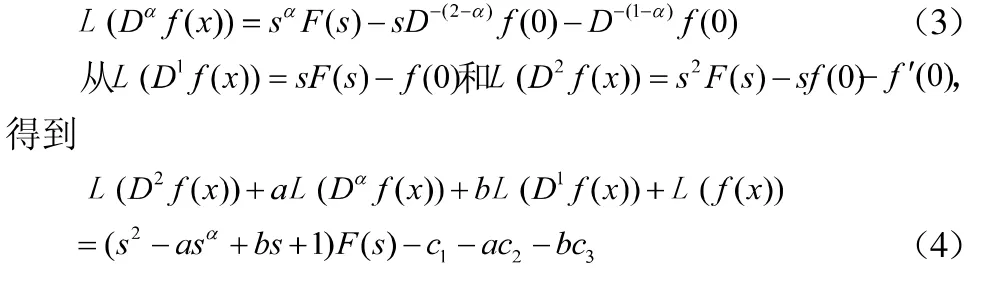拉普拉斯變換及其在分?jǐn)?shù)階微分方程拓展訓(xùn)練

申 渝 鄒馥鴻 崔嘉慧 楊 鵬

(重慶科技學(xué)院數(shù)理與大數(shù)據(jù)學(xué)院 重慶 401331)

0 引言

拉普拉斯變換是最重要的積分變換之一，在數(shù)學(xué)分析學(xué)科和工程實(shí)踐科學(xué)中有廣泛的應(yīng)用。該變換的目的是建立實(shí)變量和復(fù)變量之間的關(guān)系。如何靈活運(yùn)用這一數(shù)學(xué)工具來處理專業(yè)工程實(shí)際問題將成為一項(xiàng)重要的課題。為了更好地應(yīng)用拉普拉斯變換，本文羅列了拉普拉斯變換的基本概念及其相關(guān)重要的性質(zhì)。這些基本內(nèi)容將是處理工程實(shí)際問題的關(guān)鍵。基于拉普拉斯變換的方法是一種重要的求解常微分方程方法。我們可以根據(jù)這些拉普拉斯變換的基本知識處理某一類常微分方程，總結(jié)重要的數(shù)學(xué)技巧。分?jǐn)?shù)階微分方程是近年來重要的研究工具，在許多工程問題中得到了應(yīng)用，如圖像處理領(lǐng)域。我們將基于拉普拉斯變換的技巧拓展訓(xùn)練到求解某一類分?jǐn)?shù)階微分方程，為后續(xù)分?jǐn)?shù)階微分應(yīng)用到圖像處理中做準(zhǔn)備。

1 拉普拉斯變換及其在求解微分方程中的應(yīng)用

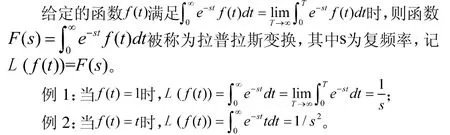
拉普拉斯變換是解決工程實(shí)際問題的強(qiáng)有力工具，其可把時(shí)域上的微分方程轉(zhuǎn)化為復(fù)數(shù)域的代數(shù)方程。拉普拉斯變換因其重要的性質(zhì)，使其在分析線性動(dòng)力系統(tǒng)時(shí)非常有用。拉普拉斯變換主要有如下重要性質(zhì)。這些性質(zhì)將用于求解微分方程。

2 分?jǐn)?shù)階微分方程的拓展訓(xùn)練

結(jié)合分?jǐn)?shù)階導(dǎo)數(shù)和拉普拉斯變換的分?jǐn)?shù)階積分給出拉普拉斯變換下的分?jǐn)?shù)階微分。假設(shè)a大于零，且n是大于a的最小整數(shù)。假設(shè)函數(shù)存在拉普拉斯變換，則

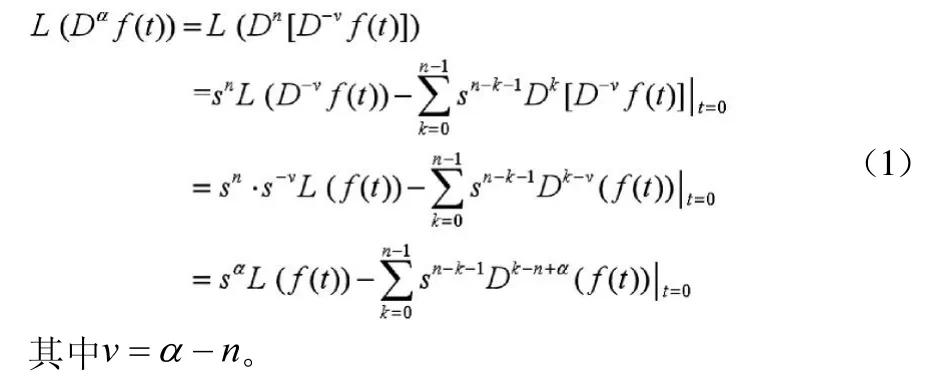
最后，借鑒傳統(tǒng)的微分方程的解法和拉普拉斯下的分?jǐn)?shù)階微分，我們訓(xùn)練拉普拉斯變換在分?jǐn)?shù)階微分方程求解應(yīng)用。假設(shè)，給定方程為