基于主成分分析-相關向量機的高速公路路基沉降量預測

張 研， 鄺賀偉

(1.桂林理工大學土木與建筑工程學院, 桂林 541004； 2.桂林理工大學，廣西巖土力學與工程重點實驗室, 桂林 541004)

隨著中國交通運輸業的迅猛發展和公路修建技術的不斷提高,高速公路成為中國連接主要城鎮的重要紐帶。路基作為高速公路關鍵組成部分及路面交通荷載承擔者,其質量的好壞直接影響著高速公路的安全使用[1-2]。路基沉降是造成高速公路路面裂縫、道路傾斜、公路塌方等工程事故的主要原因,確切了解路基沉降情況有利于及時發現安全隱患,減少交通事故發生,提高道路使用壽命[3-5]。

然而,路基沉降受到自然和人為等多種因素的影響,各個因素相互影響、交叉作用,很難精準獲得路基沉降量,很多學者關注到該問題的復雜性,開展了一系列的相關研究,如:戴少平[6]針對廣東軟土地區高速公路工后沉降問題,基于路基沉降規律及Taylor原理推導出冪多項式模型,并采用實例對該模型進行了驗證；薛凱元等[7]對黃土地區高填路段地基沉降進行觀測與分析,建立路基沉降量與地基土質量、施工速率、填土容重等4個相關參數的關系。傳統的基于現場數據建立的沉降量經驗公式難以涵蓋多種影響因素,并且存在類似工程推廣性差、精度難以保證等眾多公開問題。因此,更加適用、準確、高效的路基沉降量預測模型亟待提出。

近年來,隨著計算機科學的快速發展,學者們將機器學習技術應用于路基沉降量預測,并提出了多種預測模型,如:彭立順等[8]提出高速公路路基沉降量預測的遺傳優化神經網絡預測模型；劉文豪等[9]針對某省高速公路近10年的路基沉降量實測值,利用神經網絡和雙曲線混合的模型對路基沉降量進行預測；胡習陽等[10]分別運用基于灰色理論的GM(1,1)、Verhulst和UGM (1,1)三種模型對張桑高速公路近47 d路基沉降量數據進行分析預測,結果表明Verhulst灰色模型精度最高。然而,神經網絡方法本身存在著學習樣本過少預測精度無法保證、樣本過多泛化能力較低、本身收斂速度慢等問題；灰色模型需要求取原始序列變化規律,計算過程煩瑣、計算效率較低。尋求更加準確、合理的機器學習模型已為學術界所關注。

基于支持向量機提出的相關向量機(relevance vector machine, RVM)[11-12]機器學習方法采用了馬爾科夫性質、數據稀疏化、最大似然理論等多種數據處理技術,使得其能夠高效、高精的處理回歸問題[13-14]。然而當輸入樣本影響因素(即樣本維數)較多的時候,會降低RVM模型學習效率,增加計算成本。為此,引入主成分分析法(principal component analysis,PCA)[15-16]對影響因素進行分析,選取較少的、線性無關的影響因素組成新的輸入變量,該過程將原變量映射關系經過線性組合轉移到新變量,使得新變量剔除影響因素間的冗余信息,僅包含各種有效原始信息；然而處理后變量個數得到壓縮,達到降維的效果。采用RVM模型對新變量進行學習,建立PCA-RVM預測模型,并應用于高速公路路基沉降量預測,為高速公路路基沉降量高效、精確獲取提供一條新途徑。

1 PCA-RVM模型相關理論

1.1 PCA原理

設樣本數據集有m個樣本,每個樣本的影響因素有n個,此時構建m×n階矩陣:

(1)

在計算矩陣的協方差矩陣時,由于量綱不一致，需要對其進行標準化處理:

(2)

根據方程|λ-R|=0可計算出特征根,依據特征根λ1≥λ2≥…≥λm≥0得出對應的正交單位化特征向量為e1,e2，…，em。

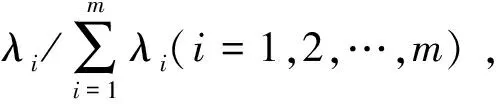
原數據矩陣經過主成分分析法降維處理后,由多個影響因素根據以下關系轉化得到綜合主成分變量y1,y2,…,yc(c≤n),得到新的變量與原影響因素關系為

(3)

1.2 相關向量機原理

RVM是一種基于貝葉斯原理的稀疏概率模型[17-18],其采用先驗參數結構下的相關決策理論來除去不相關聯的點,使得模型稀疏化,提高模型對樣本的適應性[19-20]。設訓練集為{yn,tn|n=1,2,…,N},其中，yn表示輸入訓練樣本向量值,tn表示輸出目標值且獨立分布。設tn獨立分布且帶高斯噪聲ξn,建立tn函數模型為:

tn=f(yn;ω)+ξn

(4)

(5)

式(5)中：t=[t1,t2,…,tN]T；ω=[ω0,ω1,…,ωN]T以及Φ都是由核函數預先設定的N×(N+1)矩陣,且Φ=[φ(y1),φ(y2),…,φ(yN)]T,φ(yn)=[1,K(yn,y1),K(yn,y2),…,K(yn,yN)]T。為避免過擬合現象發生,可以引入一些超參數α=(α0,α1,…,αN)T,對于不同的權重值都賦予均值為零的Gaussian先驗分布型[21]:

(6)

引用超參數以后,RVM參數后驗概率分布為P(ω,α,σ2|t),則訓練樣本后驗概率分布為

(7)

(8)

由于后驗概率分布P(ω,α,σ2|t)通過積分不能夠直接算出,故分解為

P(ω,α,σ2|t)=P(ω|t,σ,σ2)P(α,σ2|t)

(9)

整理可得,則權向量ω的分布[22]為

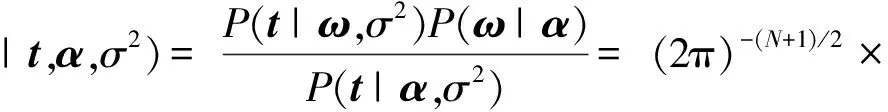
(10)

式(10)中：可以總結出概率分布服從多變量的高斯分布,Σ=(σ-2ΦTΦ+A)-1表示方差,其中，A=diag(α0,α1,…,αN)表示對角矩陣；μ=σ-2ΣΦTt表示均值。因P(α,σ2|t)不能直接計算,故利用狄拉克(Dirac Delta)函數近似計算,其表示為

(11)

αMP=argmax[P(α|t)]

(12)

(13)

對式(12)和式(13)求解可以將其轉化為

P(α,σ2|t)∝P(t|α,σ2)P(α)P(σ2)

(14)

因此,后驗概率函數分布的極值估計就轉換成極值估計,P(t|α,σ2)=N(0,C),C=σ2I+ΦA-1ΦT,則P(t|α,σ2),P(α),P(σ2)得到邊緣估計:

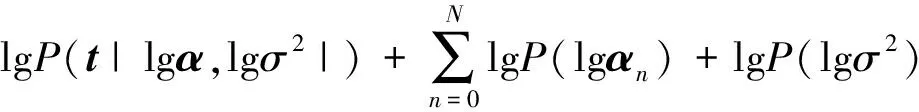
(15)

對式(15)求偏導可得

(16)

由此可得到矩陣對應的平均權重,令式(16)等于0,rn=1-αnΣnn可得

(17)

(18)

(19)

式(19)中：預測概率分布計算中,函數是兩個高斯正態分布相乘得到,所以關于t*的預測分布也服從高斯正態分布,即

(20)

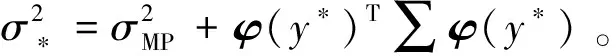
2 路基沉降量的PCA-RVM預測模型

2.1 數據樣本確定

高速公路路基沉降量影響因子復雜,選擇影響因子時經常會遇到影響因子不確定性、隨機性等一系列問題。現利用主成分分析法探究各因素與路基沉降量之間的關系,對主要因素加以分析及降維得到新變量,再利用RVM建立預測模型。根據文獻[8]綜合選取處理方式、軟土層厚、軟土壓縮模量、路堤高度、路基填筑期、竣工時沉降量等6個常規物理因子作為路基沉降主要影響因素,隨機選取22組樣本進行學習訓練,剩余的6組作為預測檢驗，如表1所示。對表1標準化處理后的28組數據的6個指標進行主成分分析,得到各個變量間相關系數情況如表2所示。

由表2可見,處理方式、軟土層厚、軟土壓縮模量、路堤高度、路基填筑期和竣工時沉降量6個影響因素之間的相關性絕對值均在0～1。基于1.1節所述各因素成分貢獻率及累計貢獻率計算方法,獲得每個因素對高速公路路基沉降量的貢獻率及累積貢獻率情況，如圖1所示。

表1 高速公路路基沉降數據集Table 1 The dataset of highway subgrade settlement

表2 各影響因素相關系數Table 2 Correlation coefficient of different influencing factors

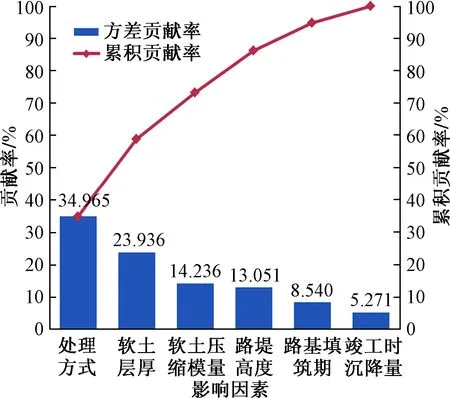
圖1 各因素貢獻率及累計貢獻率Fig.1 Contribution rate and cumulative contribution rate of each factor

由圖1可見，處理方式和軟土層厚對高速公路路基沉降量的貢獻率最大,軟土壓縮模量和路堤高度其次,路基填筑期和竣工時沉降量最小。前4個因素的累計貢獻率大于85%,說明所包含的信息足夠反映各個變量的內在關系。因此,選取前4個成分作為主成分進行分析。為研究不同影響因素在主成分變量下對應的權重,采用最大差分法得到成分得分系數如表3所示。

每個主成分變量等于各影響因素與對應成分得分系數的乘積,根據此關系可得到4個主成分變量的表達式分別為

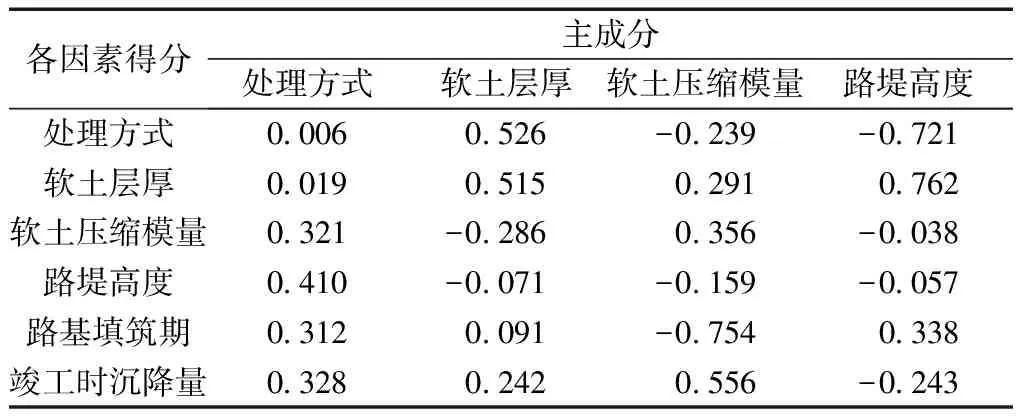
表3 成分得分系數Table 3 Component score coefficient

y1=0.006x1+0.019x2+0.321x3+0.410x4+0.321x5+0.328x6

(21)

y2=0.526x1+0.515x2-0.286x3-0.071x4+0.091x5+0.242x6

(22)

y3=-0.239x1+0.291x2+0.356x3-0.159x4-0.754x5+0.556x6

(23)

y4=-0.721x1+0.762x2-0.038x3-0.057x4+0.338x5-0.243x6

(24)

由主成分變量組成新的4×28維數據矩陣,代替了原來影響因素組成的6×28維數據矩陣,有效降低了模型維數,優化了相關因素,提高了運算效率和模型預測的準確率。

2.2 路基沉降量預測模型

基于主成分分析法對文獻[8]選取的6個主要影響因素轉化成4個主成分變量,選取4個主成分變量作為高速公路路基沉降量主要影響因子。依據PCA-RVM回歸預測模型的原理,建立基于4個主成分的PCA-RVM路基沉降量預測模型,基本原理如圖2所示。

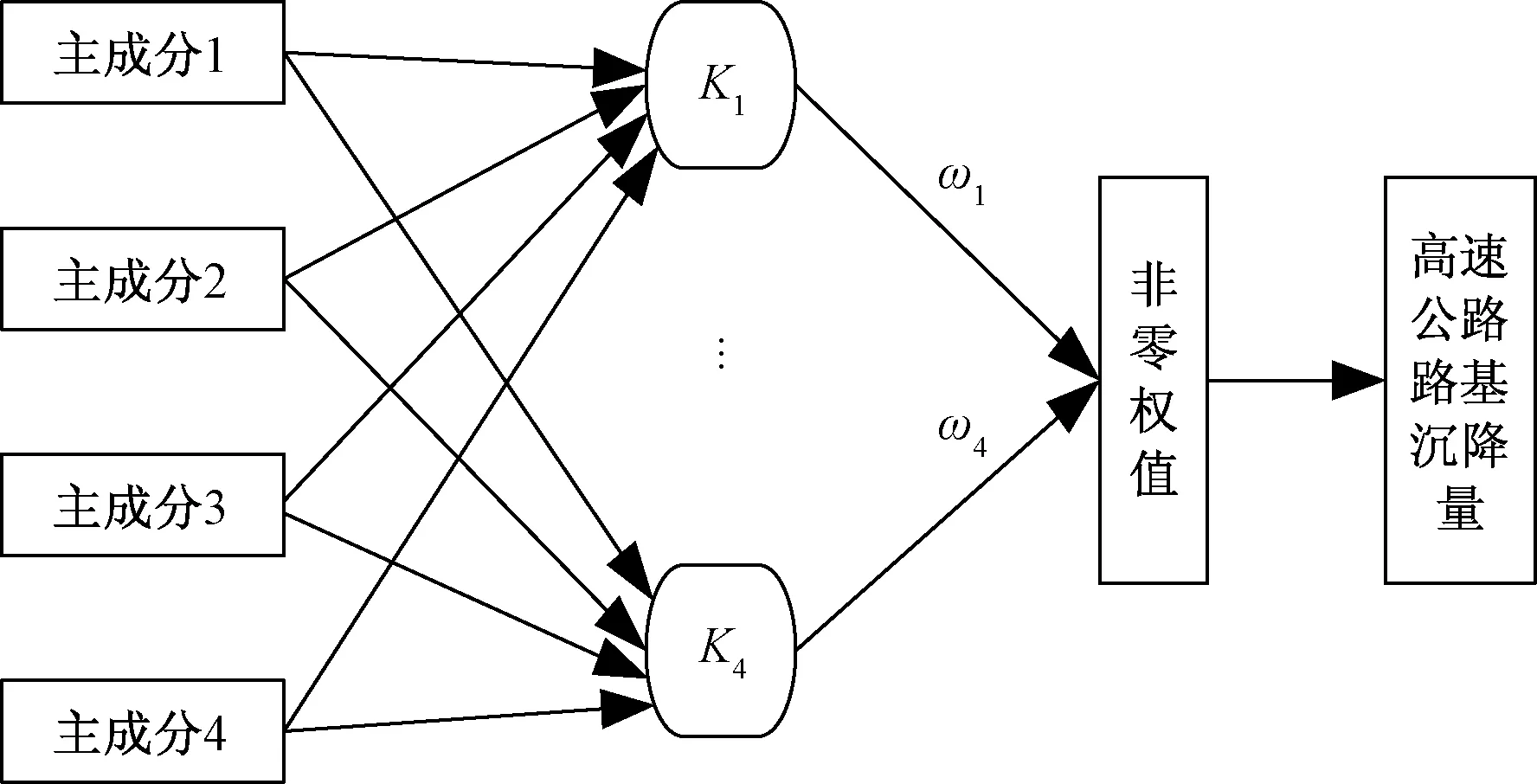
圖2 基于PCA-RVM的高速公路路基沉降量模型Fig.2 Model of highway subgrade settlement based on PCA-RVM

2.3 模型實現步驟

(1)根據高速公路路基沉降的主成分分析原理收集主成分數據,并對收集的主成分數據依照式(21)標準化處理,確定其中影響高速公路路基沉降的4個主成分為輸入,高速公路路基沉降量為輸出。

(25)

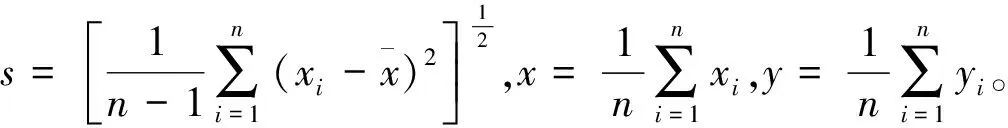
(2)選取前部分數據作為學習樣本,用于模型的擬合訓練學習；剩余數據作為預測樣本,用于模型的效果檢驗。

(3)建立PCA-RVM預測模型,對學習樣本進行訓練學習,以模型訓練的預測值和實測值的誤差作為精度要求,通過調整迭代次數、超參數尋求符合精度要求的PCA-RVM模型參數。

(4)基于上述給出的模型參數建立的PCA-RVM預測模型,對預測樣本進行預測；通過相對誤差、均方差等指標驗證PCA-RVM預測模型的精確度及可靠性。

3 應用實例分析

采用上述PCA-RVM預測模型對工程實例進行應用分析,具體數據情況如表1所示，其中前22組為數據訓練樣本,剩余6組數據為預測樣本；并在相同樣本條件下與文獻[8]所提出的RBF神經網絡、BP神經網絡、Elman神經網絡和GABP神經網絡預測結果進行對比分析。初始化MATLAB模型程序,綜合考慮并選取具有較強的局部插值能力的高斯核函數作為PCA-RVM模型RVM的核函數,對核函數參數(高斯核寬度)值分別選用0.74、0.76、0.78、0.80、0.82、0.84進行優化,不同參數取值對應的學習樣本平均相對誤差情況如圖3所示。

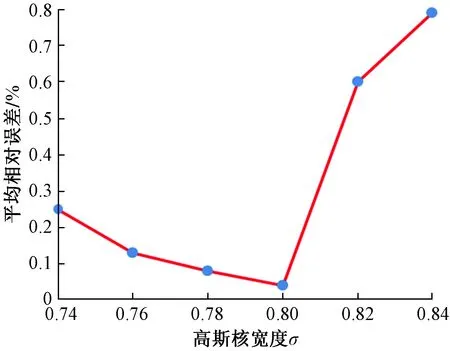
圖3 不同核寬度的學習樣本平均相對誤差Fig.3 Average relative error of learning samples with different kernel widths

由圖3可知,選取高斯核寬度σ=0.8時得到的平均相對誤差最小。故選用核寬度σ=0.8,初步擬定迭代次數為1 000。模型通過最大似然法得

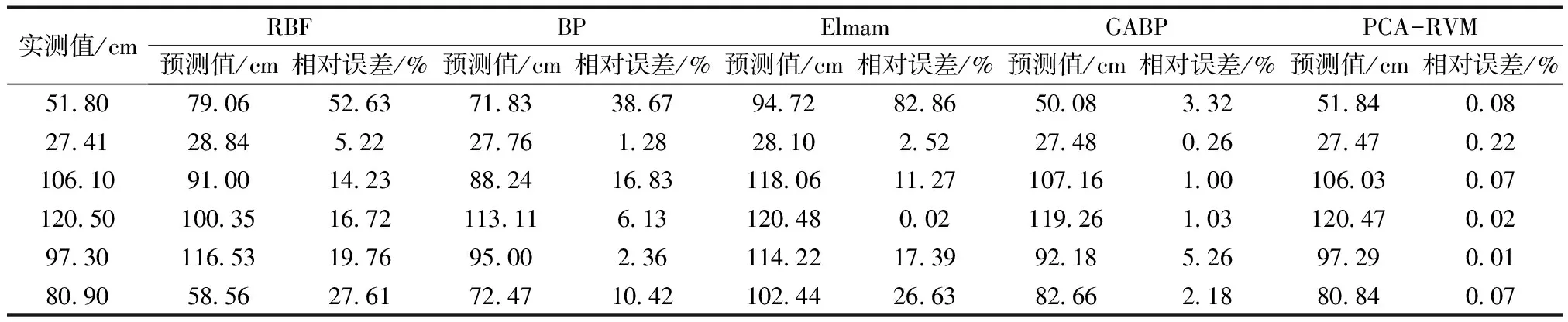
表4 不同方法的預測結果比較Table 4 Comparison of prediction results of different methods

到最優超參數α,α=[14.33 29.09 15.13 16.41 21.93 282.15 24.20 70.11 14.66 83.48 1.85 47.30 2.16 3.98 19.13 281.07 335.53 24.85 4.55 159.68 14.81 4.42 1.85 4.63 10.44],輸出對應權值ω=[0.26-0.18 0.26-0.25-0.21-0.06 0.20 0.12-0.26-0.11 0.73 0.14 0.68 0.50 0.23-0.06 0.05 0.20 0.47-0.08-0.26 0.48 0.74 0.46 0.31]。基于學習樣本及選取的參數建立預測模型,對預測樣本數據進行預測,預測結果如表4所示。

表4中列出了PCA-RVM模型預測結果以及文獻[8]中采用相同數據的4種神經網絡預測結果。在5種模型預測結果中可見:PCA-RVM模型預測結果最大相對誤差僅有0.22%；GABP模型最大相對誤差為5.26%；而Elmam模型最大相對誤差高達82.86%；BP模型最大相對誤差也有38.67%；RBF模型最大相對誤差為52.63%。由此可見,PCA-RVM模型單個樣本預測精度遠遠高于其他模型。

為了更直觀對比5種模型預測結果的樣本分布特征,將5種模型的路基沉降的預測值和實測值進行對比，如圖4所示。由圖4可見:PCA-RVM模型各個樣本預測值均比文獻[8]中4種神經網絡模型預測結果更接近真實值,幾乎與實測值曲線重合,表明PCA-RVM模型的預測精度最高；而4種神經網絡模型中GABP最好,但相比PCA-RVM模型,23號、27號樣本偏差較大略顯不足；RBF神經網絡模型、Elmam神經網絡模型和BP神經網絡模型的預測值明顯偏離了實測值,誤差過大。

圖4 不同方法預測結果Fig.4 Predicting results of different methods

為了定量化對比5種預測模型的整體預測精度和離散情況,分別計算各模型平均相對誤差(ARE)和均方差(FMSE),評判預測結果的可信賴程度和離散程度,計算公式為

(22)

(23)

式中：n為樣本數量；yi為實際值；y′i為預測值。

5種模型平均相對誤差和均方差計算結果如表5所示。

表5 平均相對誤差及均方差Table 5 Average relative error and mean square error

本文提出的PCA-RVM預測模型平均相對誤差為0.08%,均方差為0.05；GABP模型的平均相對誤差為2.17%,均方差為2.41；Elman預測模型平均相對誤差為23.45%,均方差為21.35；BP預測模型平均相對誤差為12.62%,均方差為11.91；RBF預測模型平均相對誤差為22.70%,均方差為19.36。PCA-RVM模型均比其他4種神經網絡預測模型整體預測精度更高,預測結果離散性更小,具有更高的可信度。

4 結論

建立高速公路路基沉降的精確預測模型,對路基沉降量的研究和公路災害防控等實際問題具有重要參照意義。在保證同種學習樣本數據情況下,PCA-RVM預測模型選取的影響因子更加明確,預測的結果具有較大優勢。說明了PCA-RVM預測模型精確度高、離散性更小等優點,為高速公路路基沉降預測提供一條新途徑。主要得到以下結論:

(1)高速公路路基沉降受到多種因素影響,路基沉降與影響因素之間存在著錯綜復雜的非線性關系,本文建立的PCA-RVM預測模型能夠準確篩選出相關的主成分并建立路基沉降與4個主成分的非線性映射關系,建立相對應的回歸模型,把復雜的問題簡單化,利于解決實際問題。

(2)實例表明,PCA-RVM模型在高速公路路基沉降預測得出的結果均優于4種神經網絡預測模型。說明了PCA-RVM模型選取影響因素簡單準確,具有預測結果精準度高、預測值離散度較小,可信度高等優點。

(3)PCA-RVM模型在實際工程運用中,收集廣泛的學習資料樣本有利于篩選出貢獻率較大的影響因素,總結更完整的非線性映射關系,提高PCA-RVM模型的精度及可靠度；同時,也可以結合高速公路施工現場的實際問題和設計師提出的寶貴意見合理調整參數和影響因素,可以極大改善PCA-RVM模型適用性。