基于確定性系數模型與邏輯回歸模型耦合的地質災害易發性評價
——以貴州省開陽縣為例

覃乙根, 楊根蘭*, 江興元, 魯鯤鵬, 李子安

(1.貴州大學資源與環境工程學院,貴陽 550025；2.貴州大學喀斯特環境與地質災害重點實驗室,貴陽 550025)

地質災害易發性評價又稱地質災害敏感性分析(geological hazard susceptibility),是地質災害風險評價的基礎[1]。近數十年來,隨著地理信息系統技術(GIS)的迅速發展,不少學者建立或發展了不同的地質災害易發性評價模型,其中,單一模型方面,向喜瓊等[2]將人工神經網絡模型和GIS進行有機整合,對長江三峽示范區(巴東-新灘)的區域地質災害危險性進行了分析和區劃；柳源[3]利用層次分析法對全國地質災害危險性進行了分析研究；蘭恒星等[4]、許沖等[5]、王志恒等[6]將確定性系數(CF)模型應用于區域滑坡易發性和敏感性分析方面的研究；王佳佳等[7]、余國等[8]將信息量模型應用于區域的滑坡易發性及穩定性評價；邢秋菊等[9]、趙良軍等[10]基于GIS平臺,應用邏輯回歸模型進行區域滑坡危險性評價研究。隨著定量評價模型的廣泛應用,越來越多學者關注不同模型方法的對比和優化研究,楊栓成等[11]、劉邵晨等[12]、魏江波等[13]采用確定性系數模型與層次分析相結合的方法區域地質災害危險性進行了研究；樊芷吟等[14]對汶川地區,開展了基于信息量、邏輯回歸模型以及信息量-邏輯回歸耦合模型的地質災害易發性對比研究；劉光輝等[15]以都江堰虹口鄉為例,開展了基于證據權法與確定系數法的滑坡危險區劃對比分析。以往研究表明,使用邏輯回歸(logistic regression, LR)模型和確定性(certainty factor,CF)模型進行滑坡易發性評估效果較理想因而應用較普遍,但是兩種模型也分別具有局限性,CF模型可解決評價因子內部不同特征值對易發性影響的敏感程度,卻忽略了各因子對易發性影響的差異性[13],而邏輯回歸模型在能很好地確定影響因子之間的權重大小,但不能較好解決評價因子不同特征值對易發性影響的敏感程度問題[14]。因此,將CF模型與邏輯回歸模型相結合,能夠很好地解決影響因子的權重的確定和異類數據合并的難題。

開陽縣地質條件復雜,區內地質災害頻發,根據最新的數據(2018年)顯示,開陽共有145處地質災害隱患點,給人民的生命財產安全造成巨大的威脅。而以往對開陽縣地質災害易發性方面的研究相對較少,因此,對該區的地質災害類型及分布特征進行研究,劃分地質災害的易發性區域具有十分重要的現實意義。現以貴州省開陽縣為研究區,基于GIS的柵格數據模型,分別采用CF模型、邏輯回歸模型以及CF模型和邏輯回歸模型相耦合的方法,開展貴州省開陽縣的地質災害易發性評價,通過對不同模型的易發性評價方法與預測成果及精度進行對比探討,探索更為理想的定量評估模型,為縣級區域地質災害易發性評價以及提供理論指導和技術參考。

1 研究方法

1.1 確定性系數模型

確定性系數CF為一個概率函數[11—13],其表達式為

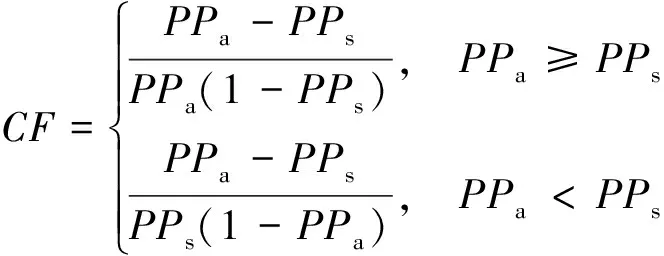
(1)

式(1)中，PPa為事件在a分類中發生的條件概率,即在數據a類單元中災害點個數與該類單元面積的比值；PPs為事件發生的先驗概率,即整個研究區地質災害隱患點數量與研究區面積的比值。

由式(1)可知,CF的變化區間是[-1,1]。CF越接近1,地質災害確定性越高,越接近-1,確定性越低；當CF接近0時,表示確定性與區域平均值接近。

1.2 邏輯回歸模型

邏輯回歸模型是二項分類變量的回歸分析模型,描述的是二元因變量和一系列自變量之間的關系[16]。在進行易發性評價時,設P為地質災害發生的概率,那么Q=1-P為地質災害不發生的概率。將P/Q取對數為ln(P/Q),則以地質災害發生概率P為因變量、影響因素集[x1,x2,…,xn]為自變量,建立回歸方程:

(2)

式(2)中，α為回歸常數；βi(i=1,2,…,n)為回歸系數；xi(i=1,2,…,n)為影響因子的指標值,于是可得邏輯回歸方程:

(3)

1.3 CF-Logistic回歸耦合模型

將CF模型計算得到的評價因子各分級的CF作為Logistic回歸分析的指標值,進行二項邏輯回歸分析,得到各影響因子的回歸系數,在此基礎上建立邏輯回歸方程,進行地質災害易發性評價。

2 案例分析

2.1 研究區概況

開陽縣地處黔中,地貌呈東西向分布的高原丘陵。開陽縣屬亞熱帶季風氣候。西部、南部降水量較多,北部降水量偏小。主要水系有烏江、清水江、谷撒河等。縣內分布著前震旦系、寒武系、石炭系、二疊系、三疊系、奧陶系和第三系、第四系地層,總體近東西向的黔中白馬洞斷裂為區內主斷裂,褶皺構造具有背斜短而寬緩呈穹狀,向斜窄而緊湊呈線狀的特點。

開陽縣主要發育地質災害包括滑坡崩塌、泥石流等,根據最新的地質災害排查數據(2018年)顯示,開陽共有145處地質災害隱患點,其中滑坡70處,崩塌35處,不穩定斜坡32處,地面塌陷和泥石流各4處如圖1所示。

圖1 開陽縣地質災害分布Fig.1 Distribution of geohazards in Kaiyang

2.2 數據來源

所采用的數據主要包括:貴州省開陽縣地質災害隱患點數據(2018年最新排查成果)；30 m分辨率數字高程數據(91衛圖助手)；1∶5萬地質圖；Landsat 8 遙感影像(地理空間數據云)；由數字高程模型(digital elevation model,DEM)提取出來的坡度、坡向和地形起伏度數據；由地質圖提取出來的水系和工程巖組數據；根據巖層傾向與坡向的夾角關系計算得到的斜坡結構數據以及根據遙感影像數據波段反射率計算得到的歸一化植被指數(normalized difference vegetation index, NDVI)等。

2.3 評價因子的選取與分級

進行地質災害易發性評價的基礎是選取評價因子。在選取地質災害發育的因素時應結合野外實地調查資料選取評價因子[17]。通過對開陽縣最新的地質災害排查數據資料的分析,結合對典型災害點的詳細勘察研究,得出開陽縣地質災害主要受地形地貌、地層巖性、地質構造及水系的控制。主要分布于河流兩岸以及斷層密集的地區,海拔低的地區災害點數明顯高于海拔高的,寒武系地層地質災害分布數量占總量的58%。

在研究開陽縣地質災害的孕災環境的基礎上,結合前人關于地質災害影響因素的研究結論[11，14],共選取高程、坡度、地形起伏度、坡向、工程巖組、斜坡結構、斷層、水系、NDVI這9個影響因子作為評價地質災害易發性的指標。結合地質災害點的發育特征對各因子進行分級,分級情況如圖2、表1所示。其中高程、地形起伏度和NDVI因子采用自然間斷法對其進行分類。

3 地質災害易發性評價

3.1 基于CF模型

基于GIS平臺,將要素圖層轉換成柵格數據,并將各圖層單元格大小設置為30 m×30 m,將各個評價因子的圖層(圖2)和地質災害點分布圖層(圖1)進行疊加分析,共得到2 217 519個獨立的屬性單元。

統計每一個分級的面積和各分級所包含的地質災害點的個數,利用CF模型計算出各分級的CF(表1)。在此基礎上進行加權求和,得到各單元地質災害易發性指數,其計算公式為[15]

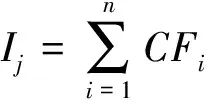
(4)

式(4)中，Ij為第j個評價單元的易發性指數；CFi為第i個影響因子各分級的CF。

3.2 基于Logistic回歸模型

隨機選取260個(130個發生,130個沒有發生地質災害)獨立單元作為易發性評價的統計樣本。其中1表示發生,0表示沒有發生,將9個影響因子的分級指標值作為自變量,是否發生地質災害作為因變量,將樣本導入SPSS 22.0軟件進行二元Logistic回歸分析,回歸結果如表2所示。邏輯回歸分析結果顯示,9個影響因子的Sig都少于0.5,說明9個因子有效 (Sig<0.5才能說明樣本顯著有效[16])。將9個因子的回歸系數代入模型,得到易發性評價的邏輯回歸公式:

(5)

式(5)中，P為發生地質災害的概率；x1～9分別表示高程、坡度、地形起伏度、坡向、工程巖組、斜坡結構、斷層、水系、NDVI這9個影響因子各分級的指標值。

3.3 基于CF-Logistic回歸耦合模型

在CF模型的基礎上,將9個影響因子各分級的CF作為自變量,是否發生地質災害作為因變量,利用SPSS 22.0軟件進行二元Logistic回歸分析(回歸結果見表3),得到邏輯回歸公式:

(6)

圖2 影響因子分級Fig.2 Evaluation of different factors

式(6)中，P為發生地質災害的概率；x1～9分別表示高程、坡度、地形起伏度、坡向、工程巖組、斜坡結構、斷層、水系、NDVI這9個影響因子各分級的CF。

表1 影響因子分級及CF

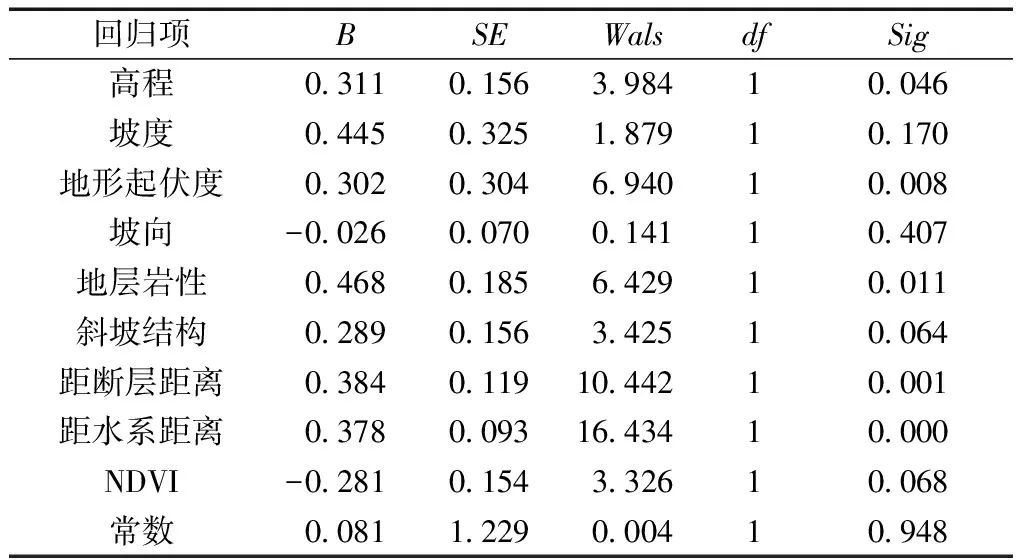
表2 邏輯回歸分析結果

注：B代表模型中各因子的回歸系數，SE為標準差，Wals為卡方值，df為自由度，Sig表示顯著性。

表3 基于確定性模型的邏輯回歸分析結果

注：B代表模型中各因子的回歸系數，SE為標準差，Wals為卡方值，df為自由度，Sig表示顯著性。

4 易發性評價結果

根據式(4)～式(6),利用ArcGIS的柵格計算器工具疊加計算出各單元的易發性指數。并根據ArcGIS自帶的自然間斷法將開陽縣易發性分為4個等級:高易發區、中易發區、低易發區、極低易發區(圖3、表4)。

表4 易發性評價結果

圖3 模型評價結果Fig.3 The evaluation results of each model

由圖3可知,地質災害高易發區主要分布于中部花梨鎮、西部金中鎮等河流以及斷層密集的地區。極低易發區主要分布于南部龍崗鎮、北部楠木渡鎮等地形較平緩、地質條件較好的地區。由表4可知,CF模型和Logistic回歸模型的易發性各分級的面積比相近；CF和Logistic回歸耦合模型中,高易發區面積占比為20.68%,高于CF模型的16.60%和Logistic回歸模型的16.94%；極低易發區的面積占比為42.68%,高于CF模型的24.23%和Logistic回歸模型的27.27%。

5 模型精度評價對比

5.1 災害點分布狀況

通過統計各易發性分級下的災害點數量占總災害點數量的百分比,可以對評價結果的準確性進行檢驗[18],統計結果如表5所示。

由表5可知,CF和Logistic回歸耦合模型中,有86.90%的地質災害點落在中-高易發區,高于CF模型的82.89%和Logistic回歸模型的80.65%。表明采用CF和Logistic回歸耦合模型的評價結果比CF模型和Logistic回歸模型更合理。

5.2 ROC曲線分析

基于SPSS 22.0平臺,進行成功率曲線(receiver operating characteristic, ROC)分析,對評價模型的精度進行檢驗(圖4),ROC曲線的線下面積(AUC)越大,表明模型的準確性越高[19-20]。由圖4可知,采用CF模型的AUC為0.853,Logistic回歸模型的AUC為0.871,CF和Logistic回歸模型結合的AUC為0.895,表明采用CF模型和Logistic回歸相結合模型的結果成功率要高于分別采用CF模型和Logistic回歸模型的結果。

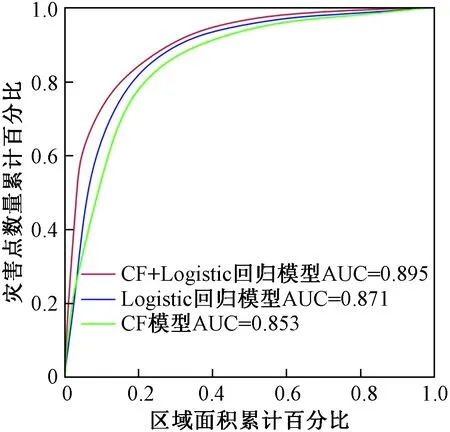
圖4 各模型ROC曲線Fig.4 The ROC curve of each model

6 結論

分別采用CF模型、Logistic回歸模型以及兩者相耦合的方法,開展開陽縣地質災害易發性評價研究,并利用災害點的分布和ROC曲線對評價精度進行檢驗，得出以下結論。

(1)耦合模型較CF模型和Logistic回歸模型的評價結果準確度更高。耦合模型中,中-高易發區的災害點百分比高于CF模型和Logistic回歸模型的占比。說明耦合模型能夠很好地解決影響因子的權重的確定和異類數據合并的難題。

(2)通過對比分析9個因子各特征值的CF和回歸系數B的大小可知,地層巖性、距斷層距離、距水系距離3個影響因子對易發性貢獻較大。特別是在距離斷層1 000 m內,距離水系800 m內和軟質巖組較易發生地質災害。

(3)耦合分析結果表明:貴州省開陽縣地質災害高易發區主要分布于花梨鎮、金中鎮等河流以及斷層密集的地區,面積為414 km2,占總面積的20.68%,極低易發區主要分布于龍崗鎮、楠木渡鎮等地形較平緩、地質條件較好的地區,面積為855 km2,占總面積的42.68%。