一類具有優自相關性質的二元序列的2-adic復雜度研究
盧櫟羽, 柯品惠
(福建省網絡安全與密碼技術重點實驗室; 福建師范大學數學與信息學院, 福建福州 350117)
1 引言
線性反饋移位寄存器(LFSRs) 和帶進位的反饋移位寄存器(FCSRs) 是兩種偽隨機序列發生器.它們所產生的序列具有良好的偽隨機性質, 如低相關性、長周期等.這些偽隨機序列在密碼學和通信系統中有著廣泛的應用.理論上, 任何二元周期序列都可以由LFSR或FCSR 生成.人們通常把能產生序列s的最短LFSRs (或FCSRs) 的長度稱為序列s的線性復雜度(或2-adic 復雜度), 用符號LC(s)(或φ2(s)) 表示.而Berlekamp-Massey 算法(BMA)[1]和FCSRs 的有理逼近算法(RAA)[2]分別是針對序列的LFSRs 和FCSRs 的有效算法.如果序列的線性復雜度或2-adic 復雜度偏低, 則該序列在密碼學意義下就是不安全的.因此, 線性復雜度和2-adic 復雜度被認為是序列的兩個重要的安全準則.而對于流密碼中的密鑰流生成器產生的周期序列, 為了抵抗RAA 其2-adic 復雜度應不小于其周期的一半.
交織技術是分析和設計序列的重要技術之一.許多最優自相關序列[3,4]、低相關序列集[5,7]、或低相關區序列集[8]都是采用交織技術設計的或者被證明具有特殊的交織結構.例如, 利用交織結構, Tang 和Gong 在文獻[3]中構造了三類具有優自相關性質的序列, 進一步地, Li 和Tang 在文獻[9]證明了這些序列具有大的線性復雜度.Arasu 等在文獻[10]中構造了一類具有最優自相關性質的序列, 進一步地, Wang 和Du 等在文獻[11]中證明其具有大的線性復雜度.后來, Tang 和Ding 在文獻[4]中給出了比文獻[3]和[10]更一般的構造.上述所提到的交織序列基本都由兩類不同的序列構成, 且它們的形式為或但是這類序列的2-adic 復雜度一直沒人計算, 直到Xiong 等在文獻[12]中提出一種利用循環矩陣去計算二元序列的2-adic 復雜度的方法, 以及Hu 在文獻[13]中提出運用自相關值的精確分布去計算二元序列的2-adic 復雜度的方法.此外, 利用循環矩陣, Xiong 等在文獻[12]中證明了所有具有理想自相關值的序列的2-adic 復雜度可達到其最大值.Xiong 等在文獻[14]中證明了兩類基于交織結構構造的序列也具有最大2-adic 復雜度.這兩類序列中的一類是由Tang 和Ding 構造的[4], 該序列具有最佳自相關性質; 另一類由Zhou 等構造[15], 該序列的相關值可達到最優的Tang-Fan-Matsufuji 界.此外, 利用文獻[13]提出的方法和精確自相關值分布, Sun 等在文獻[16]和文獻[17]中分別給出了兩類序列的2-adic 復雜度的下界.
Tang 等[4]給出了一類具有優相關性質的二元序列的構造.最近, Yan 等[18]推廣了文獻[4]的構造, 并給出了該序列的自相關值的具體分布.本文將研究該序列的2-adic 復雜度.具體地, 本文將在Tang 和Yan 等構造的二元序列的基礎上, 利用Hu 的方法, 給出這些序列的2-adic 復雜度的一個下界.全文安排如下: 第2 節給出了交織結構和勒讓德序列的定義, 并回顧了Tang 和Yan 等給出的一類具有優相關性質的二元序列的構造及其性質; 第3 節, 給出了該二元序列的2-adic 復雜度的一個下界; 第4 節對本文工作做了小結.
2 預備知識
2.1 交織結構
設v是一個正整數,si=(si(0),si(1),···,si(v ?1)),0≤i ≤u ?1 為u個周期為v的二元序列.構造一個v×u矩陣I=(Ii,j) 如下
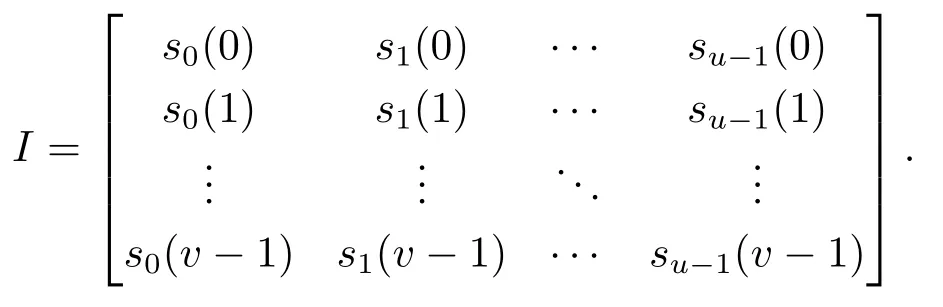
按行連接上述矩陣可得到一條長為uv的周期序列s, 稱序列s為si, 0≤i ≤u ?1 的交織序列, 記為s=I(s0,s1,···su?1), 其中I表示交織算子.
2.2 勒讓德序列
設p是一個奇素數, 勒讓德符號定義如下

其中QRp和NQRp分別為模p的二次剩余和非二次剩余.
勒讓德序列定義如下
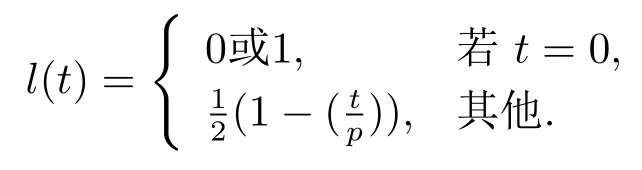
當l(0) = 1 時, 稱l(t) 為第一類勒讓德序列, 記作l(t); 當l(0) = 0 時, 稱l(t) 為第二類勒讓德序列, 記作l0(t).
設p是一個奇素數,a和b是周期為p的第一類或第二類勒讓德序列, 定義二元序列s如下

其中Lη(a) 表示序列a左循環移η位,表示a的補序列.
引理1[18]設序列s定義如上, 則
(i) 當p ≡1 (mod 4), 且a=l(t),b=l0(t) 時, 序列s的自相關值分布如下

(ii) 當p ≡1 (mod 4), 且a=l0(t),b=l(t) 時, 序列s的自相關值分布如下

(iii) 當p ≡3 (mod 4), 且a=l(t),b=l0(t) 時, 序列s的自相關值分布如下

(iv) 當p ≡3 (mod 4), 且a=l0(t),b=l(t) 時, 序列s的自相關值分布如下

3 主要結論
設N是一個正整數, ZN為模N的剩余類環.設s= (s(0),s(1),···,s(N ?1)) 為周期為N的二元序列, 定義其序列多項式為由文獻 [19]可知, 若
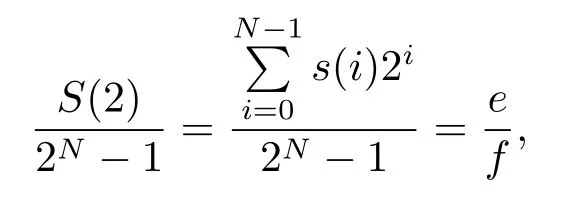
其中 0≤e ≤f,gcd(e,f)=1.則序列s的 2-adic 復雜度φ2(s)為其中z為小于或等于z的最大正整數.
引理 2[13]設s=(s(0),s(1),···,s(N ?1)) 是一條周期為N的二元序列,S(x) 為s的序列多項式, 記則
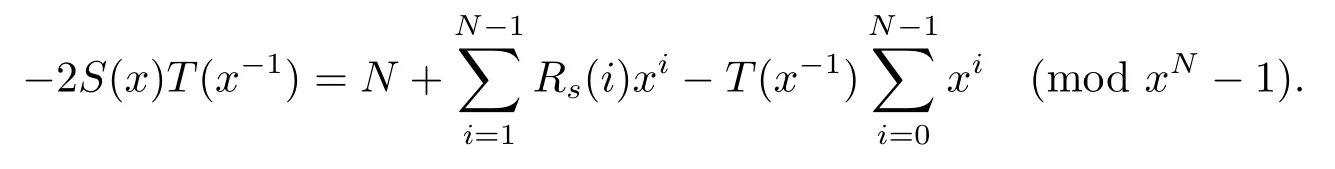
引理3設p為奇素數且p ≡1 (mod 4),s為式(2.1)定義的二元序列,其中a=l,b=l0,則有gcd(S(2),5)=1.
證由
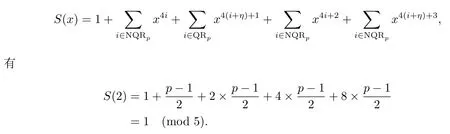
進而gcd(S(2),5)=1.
引理 4設p為奇素數, 則有
證(1) 由 22p ≡1 (mod 3) 及 22p ≡?1 (mod 5) 易知.
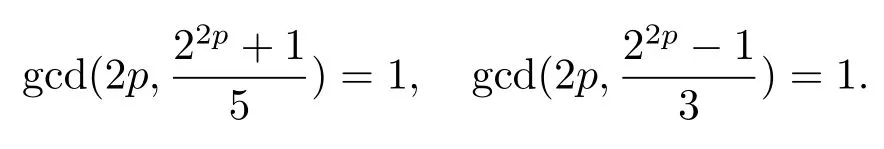
定理1設p為奇素數且p ≡1 (mod 4),s為式(2.1)定義的二元序列,其中a=l,b=l0,且則序列s的 2-adic 復雜度φ2(s) 滿足φ2(s)≥2p, 即序列s的 2-adic 復雜度大于其周期的一半.
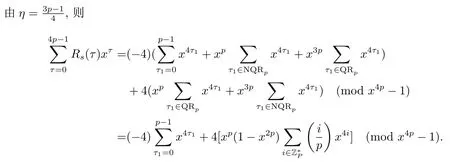
證設τ=4τ1+τ2, 其中 0≤τ1 由引理2, 有 由引理 3 及引理 4, 有 gcd(S(2),24p ?1)≤22p ?1.因此有由φ2(s) 的定義知結論成立. 推論1設p為奇素數且p ≡1 (mod 4),s為式(2.1)定義的二元序列,其中a=l0,b=l,且則序列s的 2-adic 復雜度φ2(s) 滿足:φ2(s)≥2p, 即序列s的 2-adic 復雜度大于其周期的一半. 證注意到, 該序列和定理1 中序列很相似, 差別在于交織構造中的基序列略有差異.進而它們的2-adic 復雜度的分析類似, 但是具體的計算細節也略有差異.設τ=4τ1+τ2, 其中0≤τ1 由引理2, 有 類似定理 1 的證明, 由引理 3 及引理 4, 有 gcd(S(2),24p ?1)≤22p ?1.再由φ2(s) 的定義知結論成立. 引理5設p為奇素數且p ≡3 (mod 4),s為式(2.1)定義的二元序列,其中a=l,b=l0,其序列多項式為S(x), 則有gcd(S(2),3)=1. 證由 進而gcd(S(2),3)=1. 定理2設p為奇素數且p ≡3 (mod 4),s為式(2.1)定義的二元序列,其中a=l,b=l0,且則序列s的 2-adic 復雜度φ2(s) 滿足φ2(s)≥2p, 即序列s的 2-adic 復雜度大于其周期的一半. 證設τ=4τ1+τ2, 其中 0≤τ1 由引理2, 有 再由φ2(s) 的定義, 有 因此結論成立. 推論2設p為奇素數且p ≡3 (mod 4),s為式(2.1)定義的二元序列,其中a=l0,b=l,且則序列s的 2-adic 復雜度φ2(s) 滿足φ2(s)≥2p, 即序列s的 2-adic 復雜度大于其周期的一半. 證注意到, 該序列和定理2 中序列很相似, 差別在于交織構造中的基序列略有差異.進而它們的2-adic 復雜度的分析類似, 但是具體的計算細節也略有差異.設τ=4τ1+τ2, 其中0≤τ1 由引理2, 有 由引理4 及引理5, gcd(S(2),24p ?1)≤22p+1.再由φ2(s) 的定義可知 本文研究了一類具有優自相關性質的二元序列的2-adic 復雜度, 給出了該類序列的2-adic 復雜度的一個下界.本文的結果表明這類序列的2-adic 復雜度不小于其周期的一半,這意味著這些序列可以抵抗針對帶進位的反饋移位寄存器的有理逼近算法的攻擊.
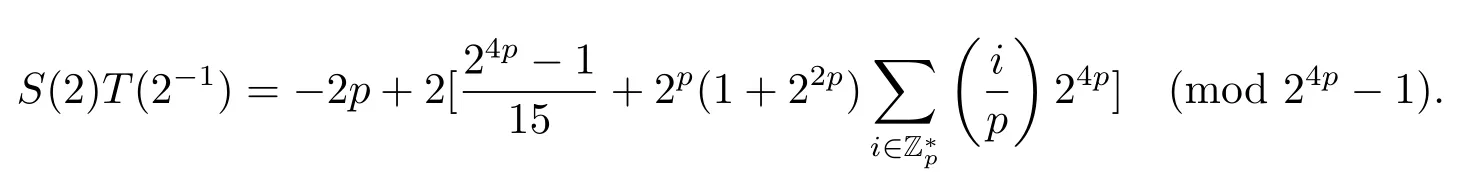
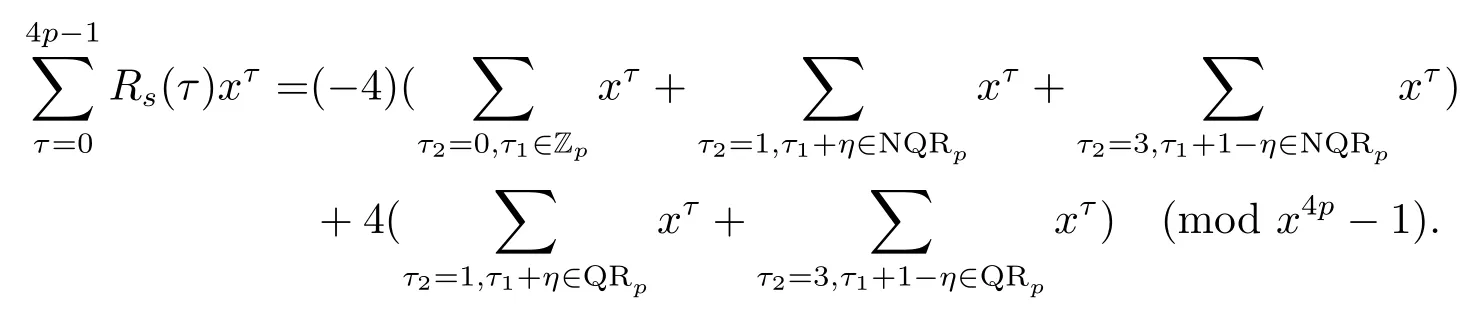

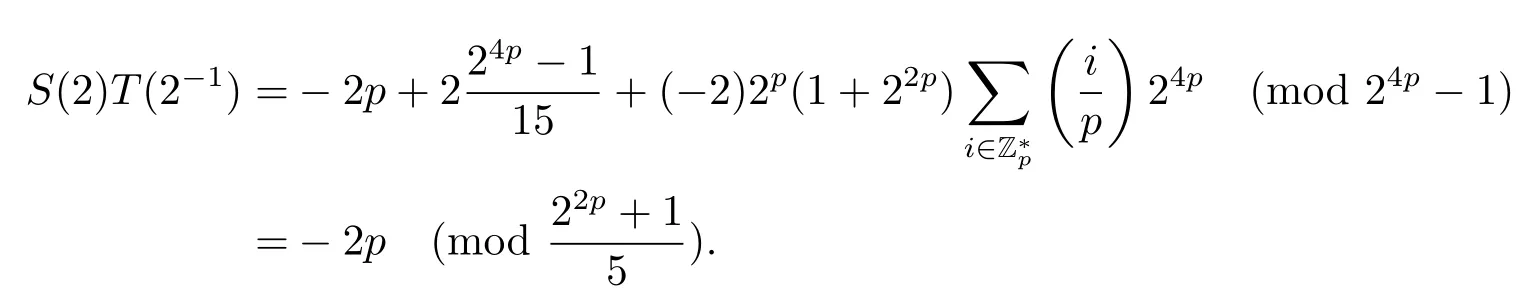
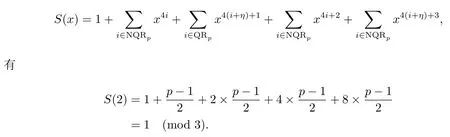
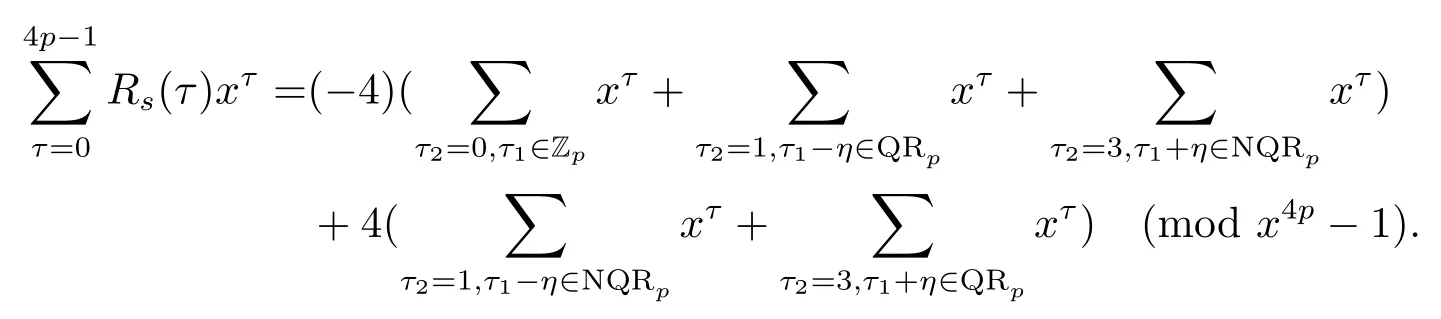

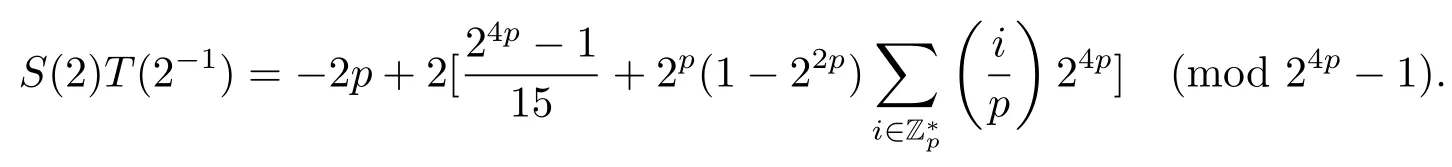
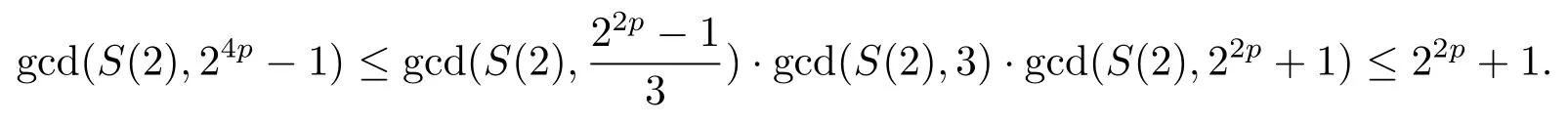
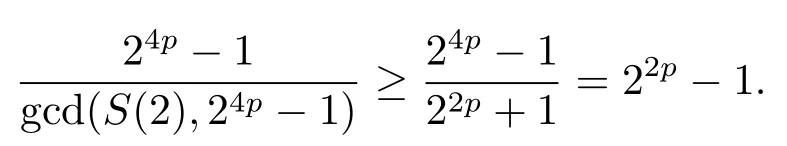
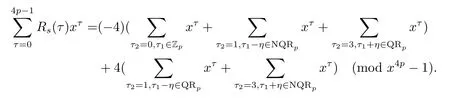
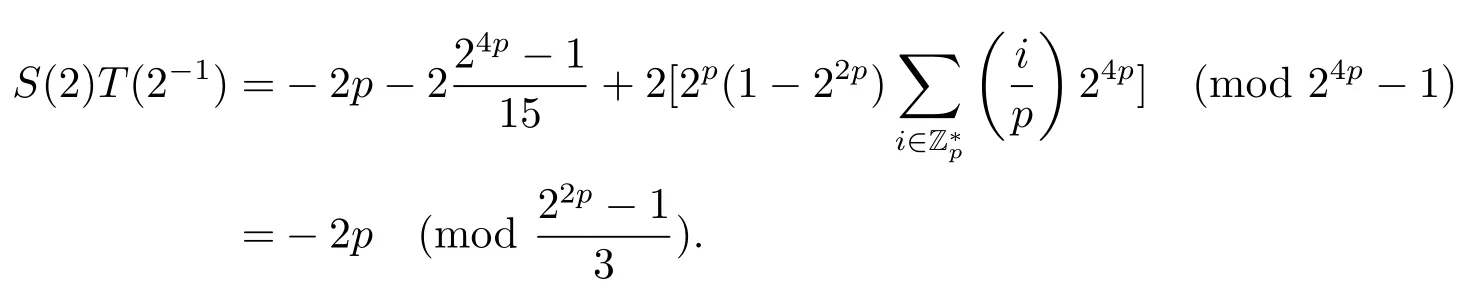
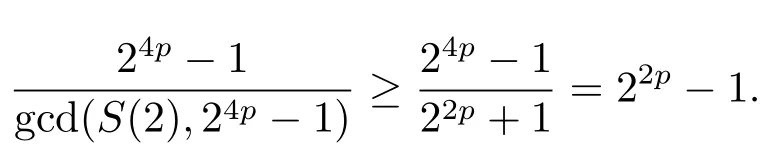
4 總結

