n-角范疇的局部化

王敏雄, 鄭 燕

(華僑大學數學科學學院,福建 泉州 362021)

1 引言

三角范疇[1]是同調代數中的核心概念.在最近的發展中, 三角范疇成為數學中的重要工具和研究對象, 是描述數學和數學物理中許多復雜研究對象的基本語言和分類新依據．高維同調代數由Iyama[2?3]引入并發展, 它也被稱為n- 同調代數．繼三角范疇的發展以及高維同調代數的引入后,n- 角范疇[4]自然而然地被提出．n- 角范疇是三角范疇的一種推廣形式,經典三角范疇就是n- 角范疇中n=3 的特殊情況．給定一個n- 角范疇K, 有時需要得到一個新的n- 角范疇,使得兩者對象相同,但對于n- 角范疇K的某個態射集S, 在新范疇中成為同構.為滿足這種需求, 可引入n- 角范疇的局部化理論, 即通過局部化方法構造商范疇.

2 預備知識

定義2.1[5]設K是一個加法范疇,S是K中某些態射做成的類,S稱為K的一個乘法系, 如果滿足下述條件：

(FR1)S對于態射的合成是封閉的, 即若s:X →Y和t:Y →Z是S中的態射, 則它們的合成ts也是S中的態射; 并且對于K中的任意對象X, 其恒等態射idX屬于S;

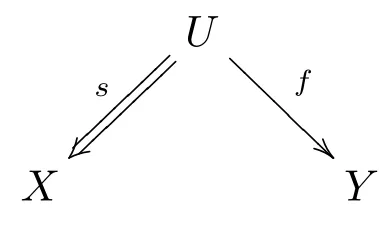
(FR2) 對于K中每個態射圖

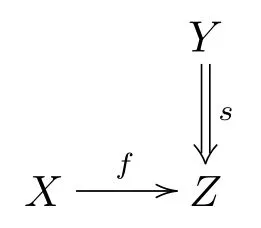
這里s ∈S, 存在K中的態射g:W →Y和S中的態射t:W →X使得下圖可交換.

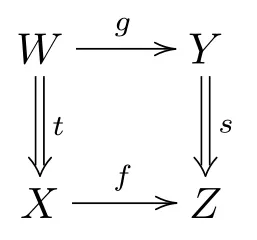
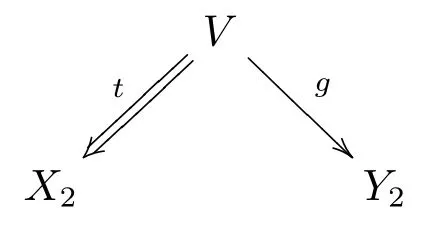
對偶地, 對于K中每個態射圖

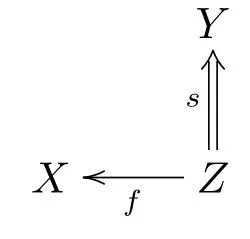
這里s ∈S, 存在K中的態射g:Y →W和S中的態射t:X →W使得下圖可交換

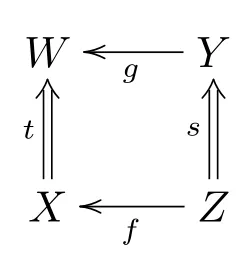
(FR3) 設f,g:X →Y是K中的兩個態射.那么存在S中的態射s:Y →Z使得sf=sg當且僅當存在S中的態射t:W →X使得ft=gt.

乘法系S稱為飽和的, 若S滿足gf,kg ∈S蘊含著g ∈S.

設K是一個加法范疇,S是K的一個乘法系, 對K中的任意兩個對象X,Y, 定義K中從X到Y的右分式(f,s) 為態射圖其中s ∈S.從X到Y的兩個右分式 (f,s), (g,t) 稱為等價, 記為 (f,s)～(g,t), 若有交換圖

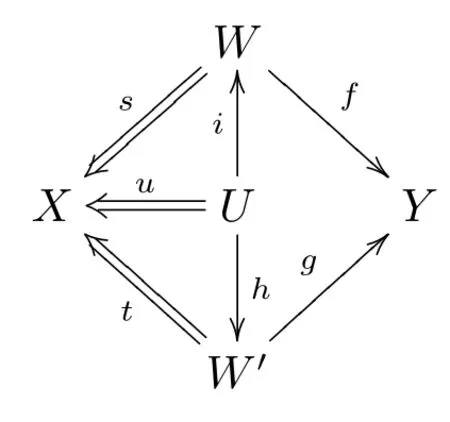
其中u ∈S.易證右分式的等價是一個等價關系.記 (f,s) 的等價類為f/s.

定理2.1[5]設K是一個加法范疇,S是K的一個乘法系, 那么下列結論成立.

(a)S?1K是一個加法范疇, 其中S?1K的對象是K中的對象;S?1K中從對象X到對象Y的態射集 HomS?1K(X,Y) 是K中X到Y的右分式所有等價類作成的集合.

(b) 局部化函子F:K →S?1K是加法函子, 其中對K中的任意對象X,F(X)=X;對任意的K中態射f:X →Y,F(f)=f/idX.且若s ∈S, 則F(s) 是S?1K中的同構.

(c) 對于加法函子H:K →C, 若s ∈S,H(s) 是C中的同構, 則存在唯一一個加法函子G:S?1K →C使得H=GF.

(d) 若S是飽和的, 則F(f) 是同構當且僅當f ∈S.

3 n-角范疇的局部化

定義3.1設 (K,Σ,Θ) 是一個n- 角范疇,K的一個乘法系S稱為相容乘法系, 若滿足

(FR4) 對于任意態射s,s ∈S當且僅當 Σs ∈S;

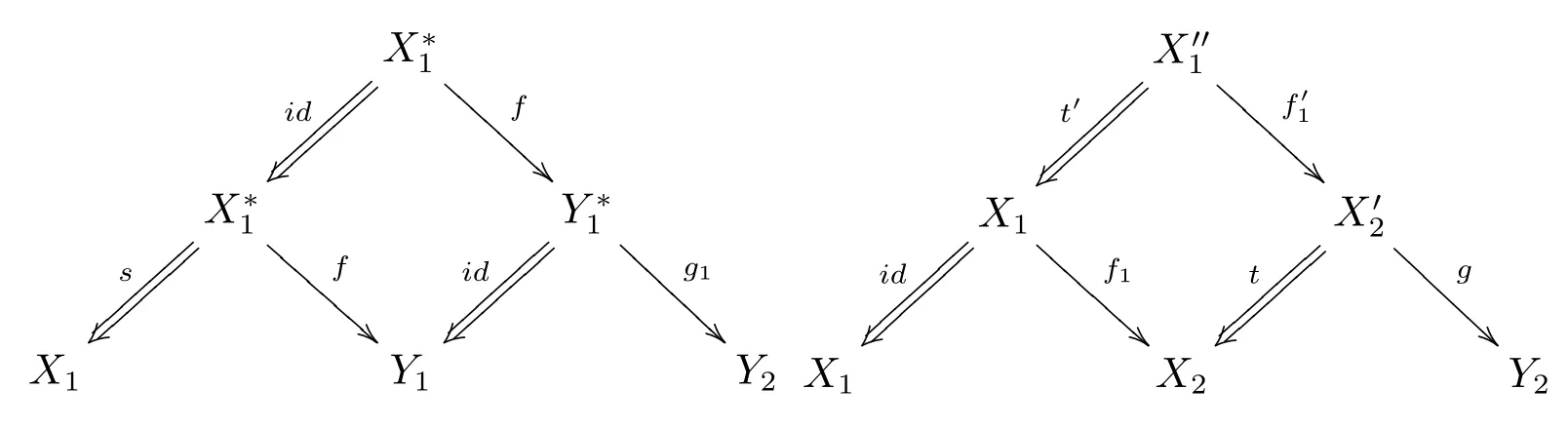
(FR5) 設下圖中上下兩行均為n- 角,?1,?2∈S, 并且左邊第一個方塊可交換

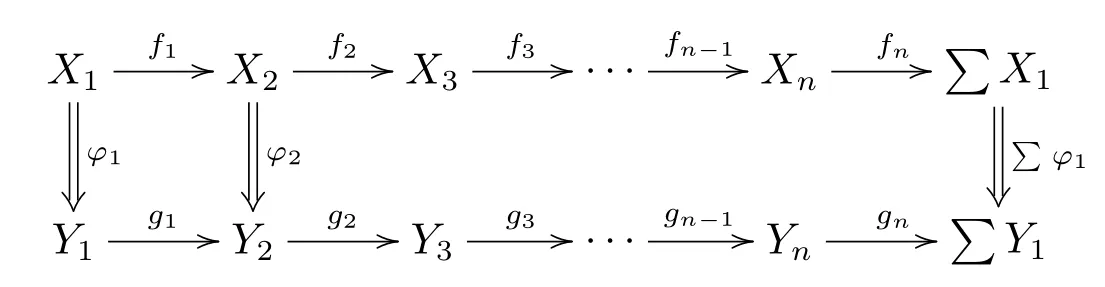
則存在?i:Xi →Yi ∈S, 3≤i ≤n, 使得下圖為n- 角態射

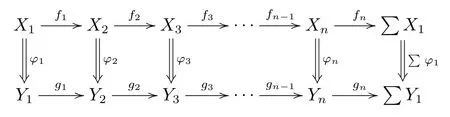
定義 3.2[6]設 (K,Σ) 和是兩個n- 角范疇, 函子稱為n- 角函子, 若滿足

(a)L是加法函子.

(c)L保持n- 角, 即若是K中的n- 角, 則是中的n- 角.

定理3.1設 (K,Σ,Θ) 是一個n- 角范疇,S是K的一個相容乘法系.則

(1)K的自同構 Σ 誘導S?1K的自同構, 仍記為 Σ, 這里 Σ(b/s) = Σb/Σs; 并且(S?1K,Σ,) 也是n- 角范疇, 這里中的元素同構于以下的n-Σ- 序列

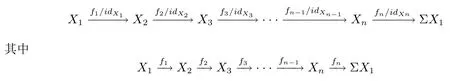
是K中n- 角.

(2) 局部化函子F:K →S?1K是n- 角函子; 對任意的s ∈S,F(s) 是同構; 若H:K →C是n- 角函子, 并且使得對任意的s ∈S,H(s) 是同構, 那么存在唯一的n- 角函子G:S?1K →C使得H=GF.

(3)S?1K中,是使得F:K →S?1K是n- 角函子的唯一的n- 角結構.

證(1) 下面證明滿足(N1)–(N4), 從而(S?1K,Σ,) 是n- 角范疇.

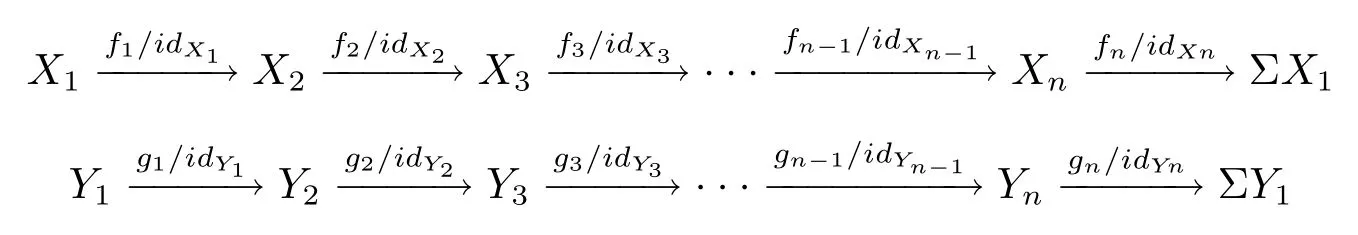
因此有K中的兩個n- 角

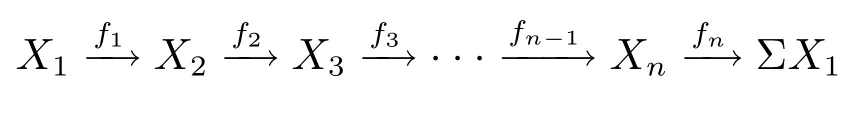
由于 (K,Σ,Θ) 是n- 角范疇, 所以 Θ 對直和封閉, 因此有

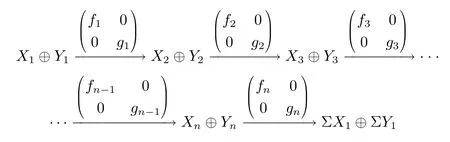
屬于 Θ, 其在F下的像為如下n-Σ- 序列

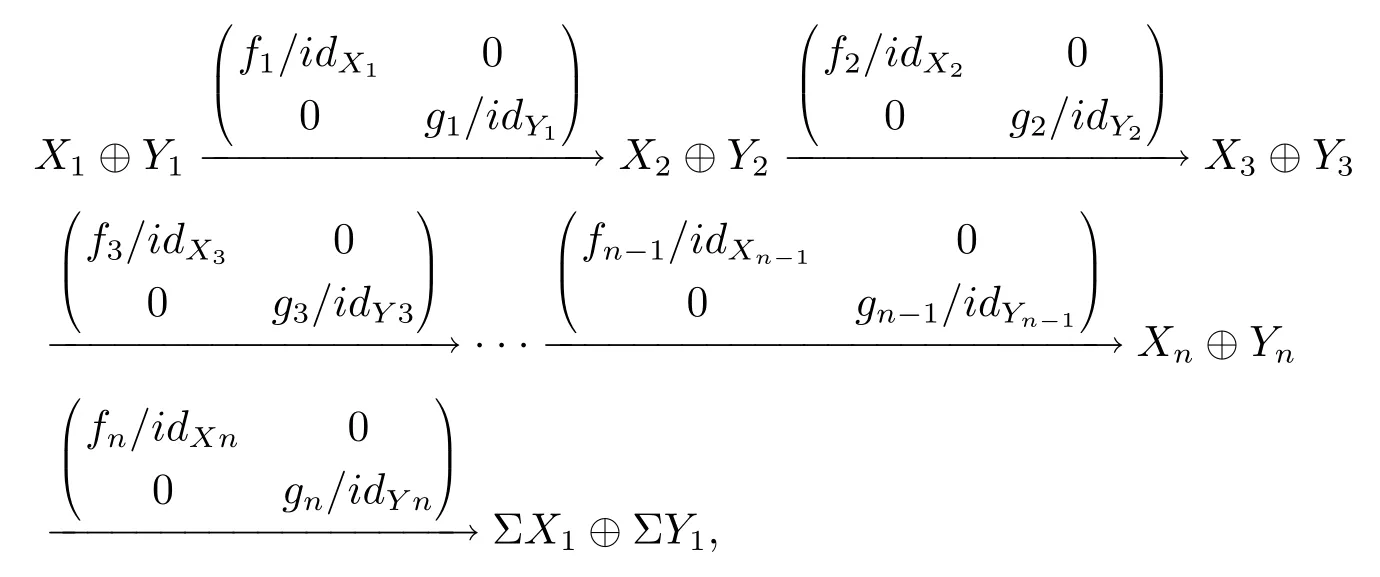
所以此n-Σ- 序列屬于, 即對直和封閉.

同理, 可以得到在S?1K中對直和項亦封閉.

(b) 設f/s:X →Y是S?1K中的態射, 那么可以用右分式表示如下

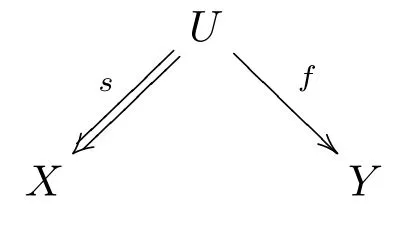
這里s ∈S.因為K是一個n- 角范疇, 因此由態射f:U →Y,K中存在如下n- 角

考慮下圖

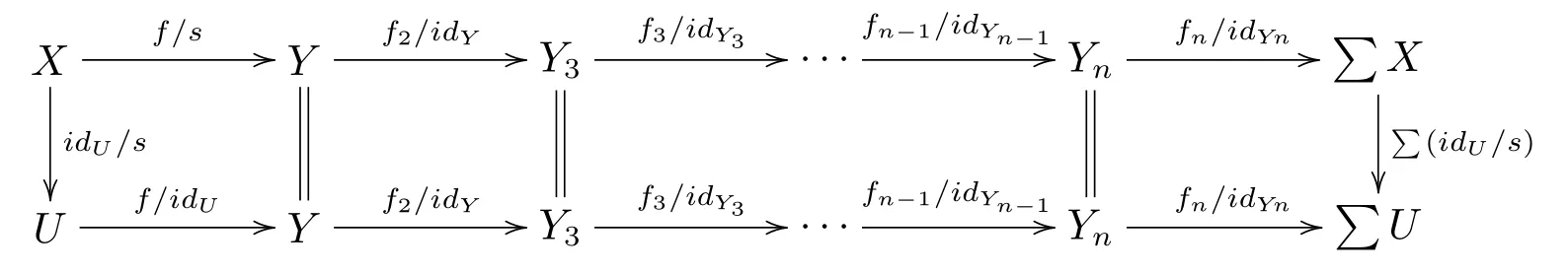
(c) 設X是S?1K中的一個對象, 因此它也是K中的一個對象, 那么有K中n- 角因此可知包含以下平凡n-Σ- 序列

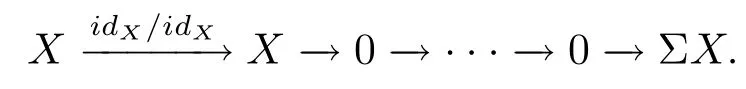
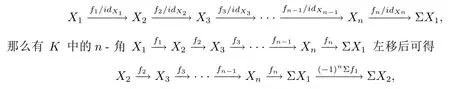
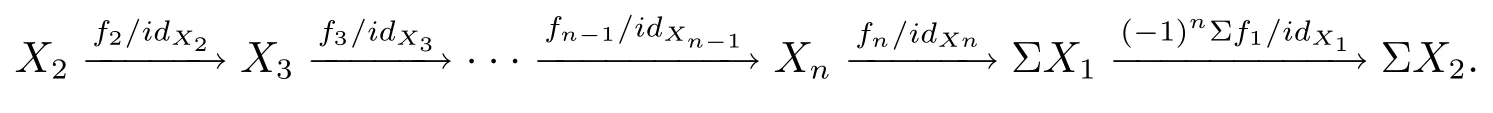
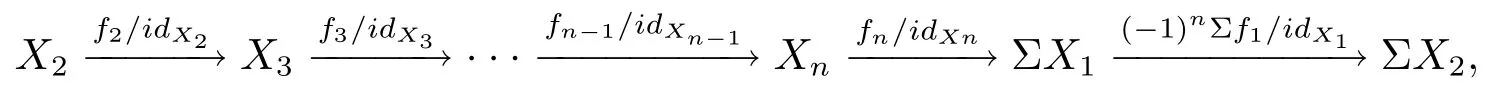
那么有K中的n- 角

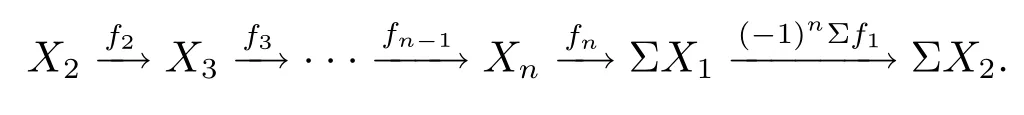
由于K是n- 角范疇, 則 Θ 包含n- 角

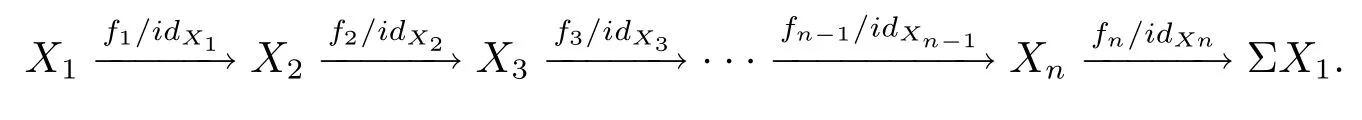
因此(N2) 成立.

(N3) 給定以下交換圖

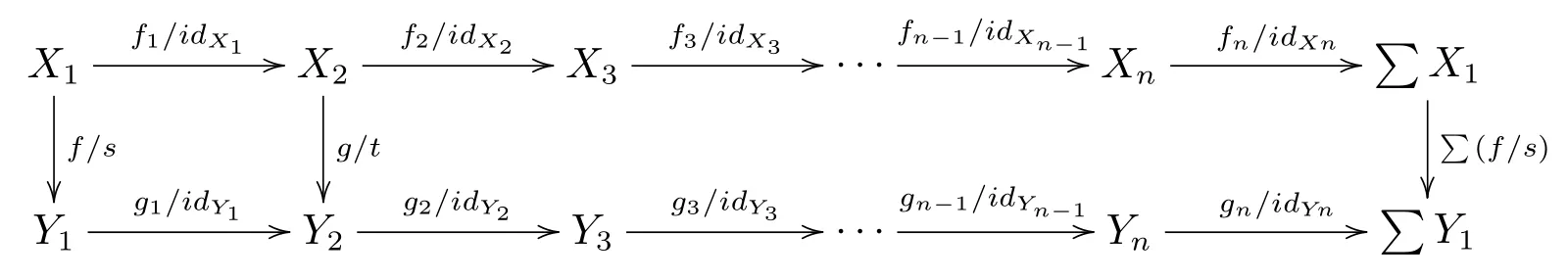
和

由于左邊第一個方塊是可交換的, 所以有

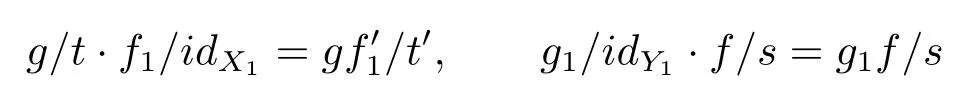
且兩式相等

有交換圖

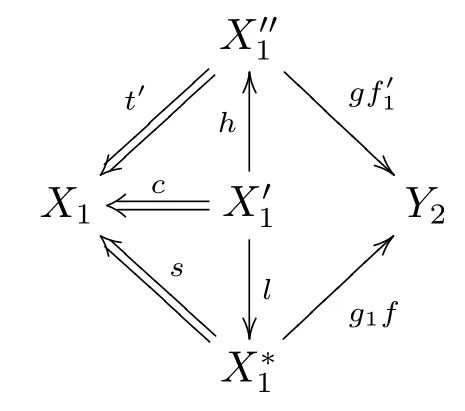
因此根據(FR5) 可知有如下交換圖

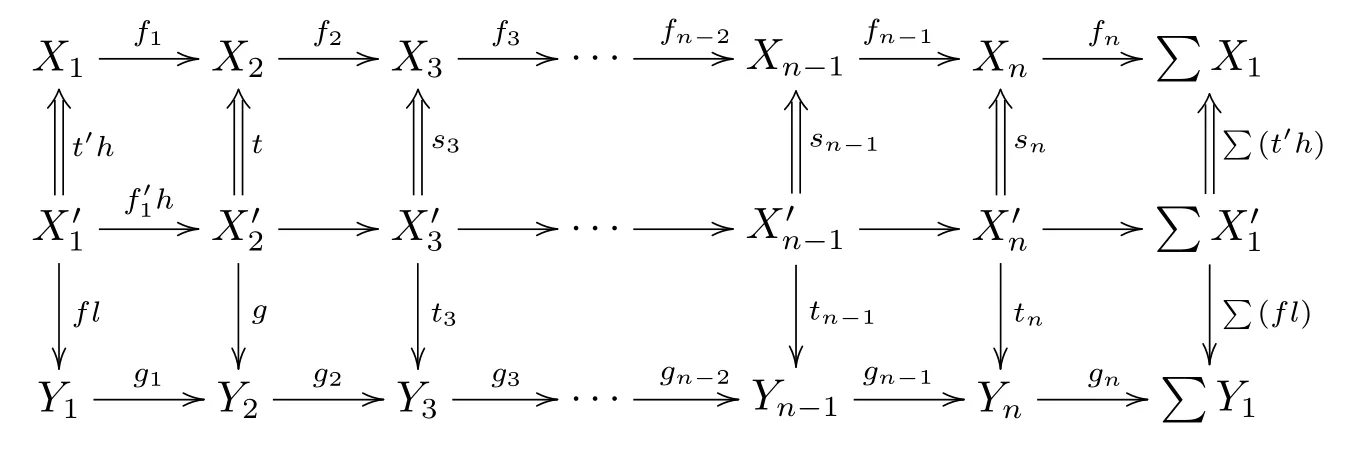
那么, 得到S?1K中的態射ti/si:Xi →Yi, 3≤i ≤n, 并且這些態射可使得下圖可交換

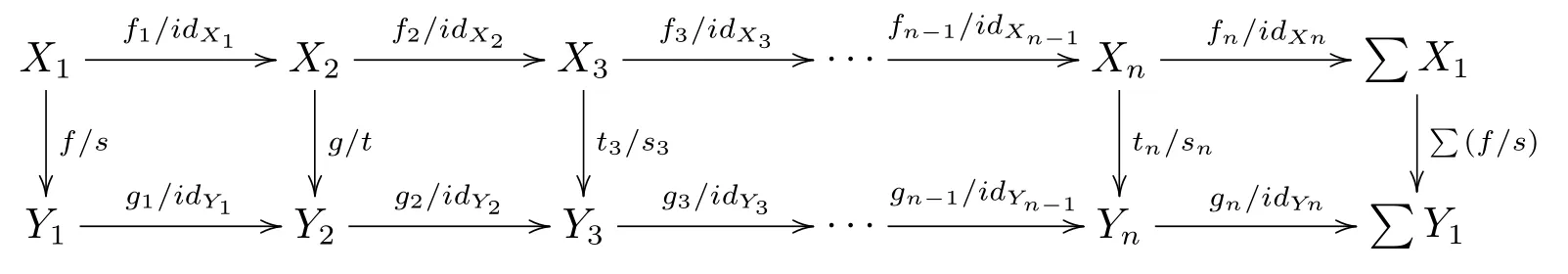
從而(N3) 成立.

(2) 由于S?1K中的標準n- 角是指K中的n- 角在局部化函子F:K →S?1K下的像, 因此可知F是n- 角函子.由于H:K →C是n- 角函子, 且對任意的s ∈S,H(s)是同構, 則由定理2.1 可知存在唯一一個加法函子G:S?1K →C使得H=GF, 加法函子G是n- 角函子可由等式H=GF來保證.

(3) 若還有一個滿足條件的n- 角結構的定義知根據文獻[4, 命題2.5(c)]知,

定義3.3設 (K,Σ,Θ) 是一個n- 角范疇,A是Abel 范疇.加法函子Q:K →A稱為一個上同調函子, 若對K中任意n- 角均有A中的正合列

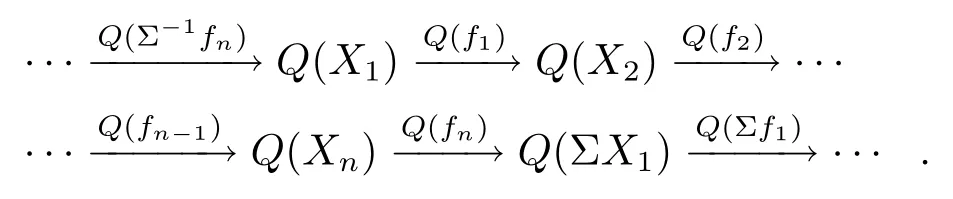
命題3.1設K是n- 角范疇,A是Abel 范疇,Q:K →A是一個上同調函子,S是K的一個相容乘法系, 且滿足若s ∈S,Q(s) 是A中的一個同構, 那么存在唯一一個上同調函子FS:S?1K →A使得下圖可交換

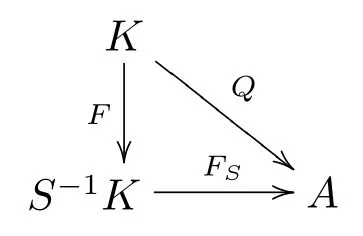
證加法函子FS:S?1K →A的存在性和唯一性可由定理2.1 保證.下面證明FS是上同調函子.

并且有S?1K中的n- 角同構

通過作用FS, 得到A中的交換圖

因為Q是上同調函子, 且上述交換圖的第一行是A中的正合列, 因此第二行也是正合的,故FS是上同調函子.

定義3.4[6]設 (K,Σ,Θ) 是n-角范疇,K的加法滿子范疇G稱為n-角子范疇,若G對同構封閉, Σ 是G的自同構, 并且G對擴張封閉, 即對任意K中態射fn:Xn →ΣX1,其中X1,Xn ∈G, 均存在K中n- 角使得X ∈G,i2≤i ≤n ?1.

注在三角范疇局部化理論中, 飽和相容乘法系與厚子范疇之間存在一一對應關系, 其中用到三角的如下重要性質.設是三角, 則f1是同構當且僅當但在n- 角范疇 (n>3) 時并沒有類似的n- 角性質, 從而不容易在n- 角范疇的飽和相容乘法系與n- 角子范疇之間建立對應.

引理3.1設 (K,Σ,Θ) 是n- 角范疇,是n- 角,則下列敘述等價

(1)Xn=0;

(2)fn?1=0,fn=0;

(3)f1為可裂單,fn?2為可裂滿.

證(1)由于fn=0, 根據文獻[8, 引理2.3]知fn?1為可裂滿, 所以存在態射g使得fn?1·g=idXn, 又fn?1=0, 從而Xn=0.再根據文獻[8, 引理2.3]易知

命題3.2設S是n- 角范疇K的相容乘法系,F:K →S?1K是局部化函子.令

則 Ψ(S)?KerF.進一步, 若S飽和, 則 Ψ(S)=KerF.

證設Xn ∈Ψ(S), 則在S?1K中有標準n- 角

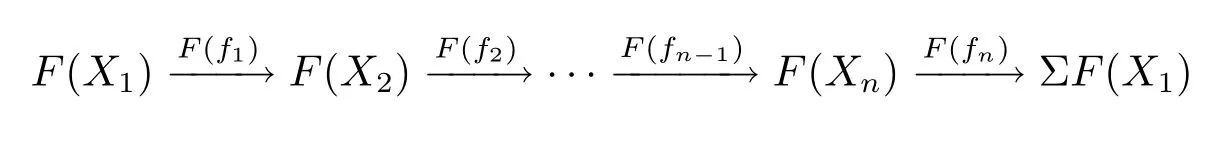
且F(f1),F(fn?2) 為同構, 由引理3.1 知Xn ∈KerF.