素的?-代數上的非線性混合Lie三重ξ-導子

周 游, 楊柱俊, 張建華

(1.曲阜師范大學數學科學學院, 山東曲阜 273165)

(2.陜西師范大學數學與信息科學學院, 陜西西安 710062)

1 引言

設A是一個?-代數,對于任意的A,B ∈A,將[A,B]=AB?BA與[A,B]?=AB?BA?分別定義為A和B的 Lie 積與斜 Lie 積, 將滿足L([A,B]) = [L(A),B]+ [A,L(B)]與L([A,B]?)=[L(A),B]?+[A,L(B)]?的映射分別稱為 Lie 導子和斜 Lie 導子.

近年來, 已經有許多學者對Lie 積與斜Lie 積性質的刻畫做出了很大貢獻.例如, 很多學者對代數上的Lie 三重導子, 斜Lie 三重導子, 保持斜Lie 三重積的映射, 混合Lie 三重導子以及保持混合Lie 三重積的映射等問題進行了深入的研究, 其詳細工作可參見文獻[1–8].

在本文中我們將給出一個復數域上的有單位元和非平凡投影的素的?- 代數M上的混合 Lie 三重ξ- 導子的結構, 即對任意的A,B,C ∈M,L滿足:L([[A,B]?,C]ξ) =[[L(A),B]?,C]ξ+[[A,L(B)]?,C]ξ+[[A,B]?,L(C)]ξ, 且ξ1 時, 則可得L是一個可加的 ?-導子, 且對任意的A ∈M, 有L(ξA)=ξL(A).

2 可加性

在這一小節中，我們將證明如下定理.

定理2.1設M是一個有單位元和非平凡投影的素的?- 代數,L:M →M是一個混合 Lie 三重ξ- 導子, 其中1.則L是可加映射.

設P1為M中的一個非平凡投影,I是M中的單位元和P2=I ?P1.令Mij=PiMPj(i,j=1,2)，則且其兩兩相交均為{0}.因為M是一個素代數, 所以對任意的A ∈M, 若對任意的Bkl ∈Mkl, 均有ABkl=0, 則可得APk=0.

在證明此定理前, 我們首先給出一系列的引理.

引理2.1L(0)=0.

證很容易驗證L(0)=L([[0,0]?,0]ξ)=0.

引理2.2設Aij ∈Mij(i,j=1,2), 則

證設對任意的有

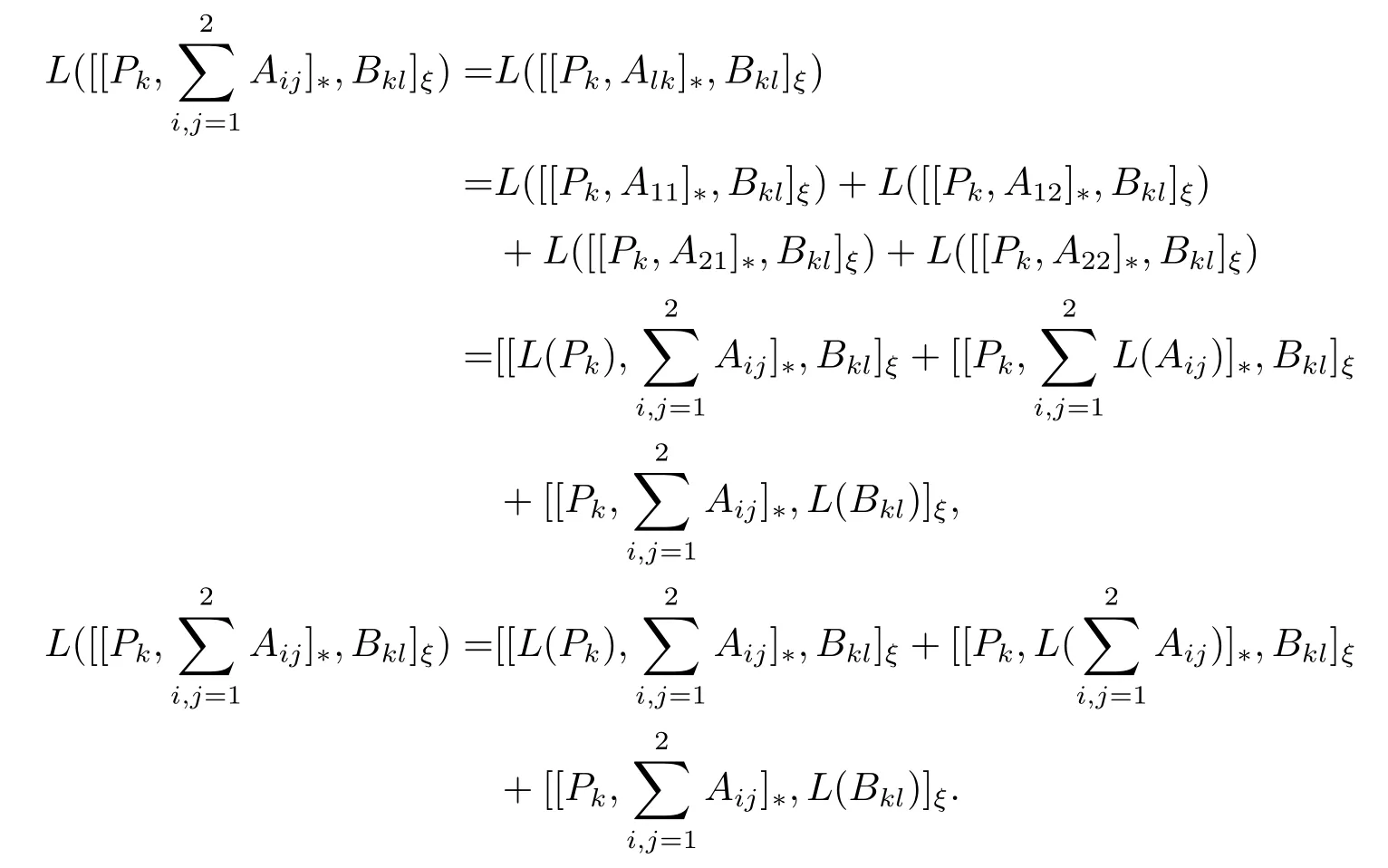
由此可知 [[Pk,T]?,Bkl]ξ=0, 故另一方面則有

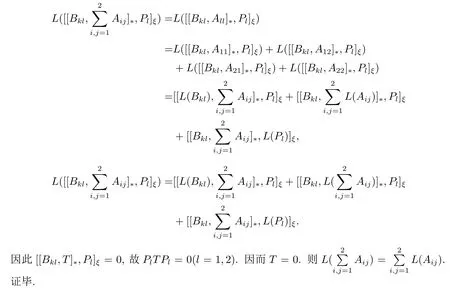
引理 2.3設則L(Aij+Bij)=L(Aij)+L(Bij).

證由引理 2.2 可知, 對任意的有

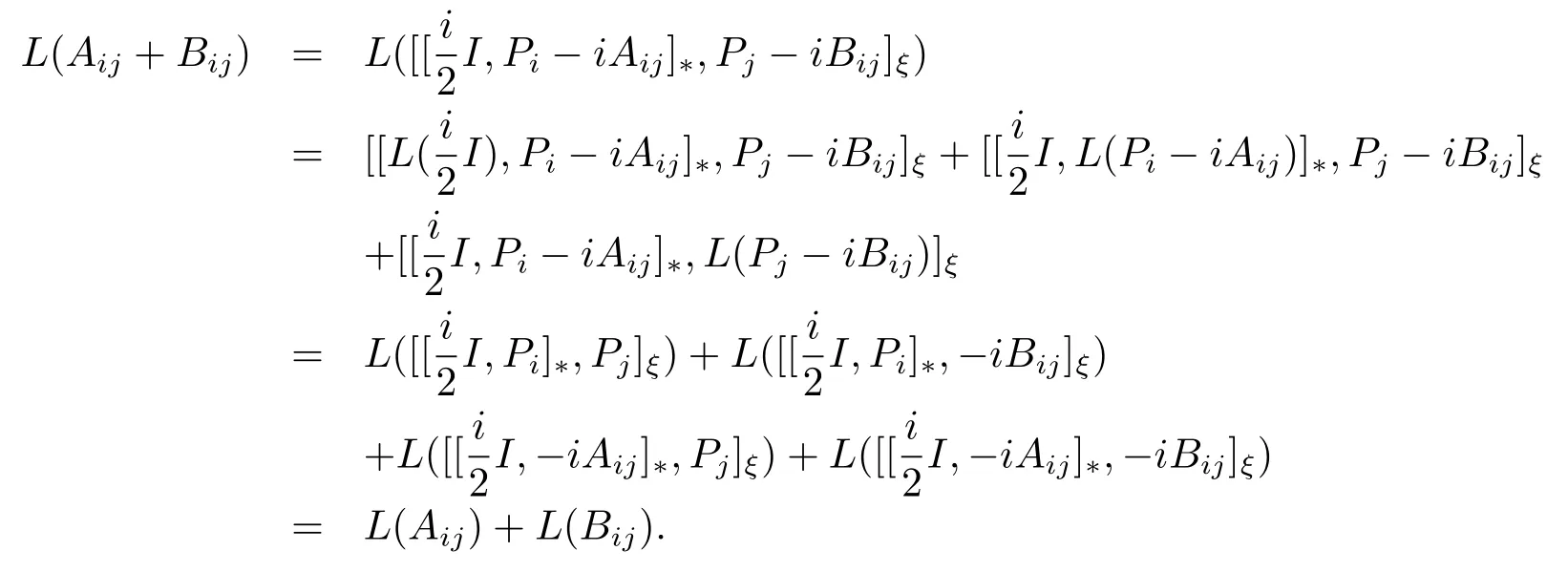
證畢.

引理2.4設Aii,Bii ∈Mii,i=1,2, 則L(Aii+Bii)=L(Aii)+L(Bii).

證令T=L(Aii+Bii)?(L(Aii)+L(Bii)).則易驗證,

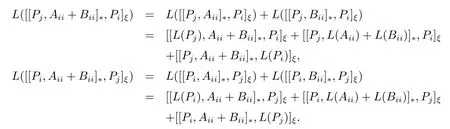
故 [[Pj,T]?,Pi]ξ=[[Pi,T]?,Pj]ξ=0, 則可推出PiTPj=PjTPi=0.

由引理 2.2 和引理 2.3 知, 對任意的Cij ∈Mij,ij, 有

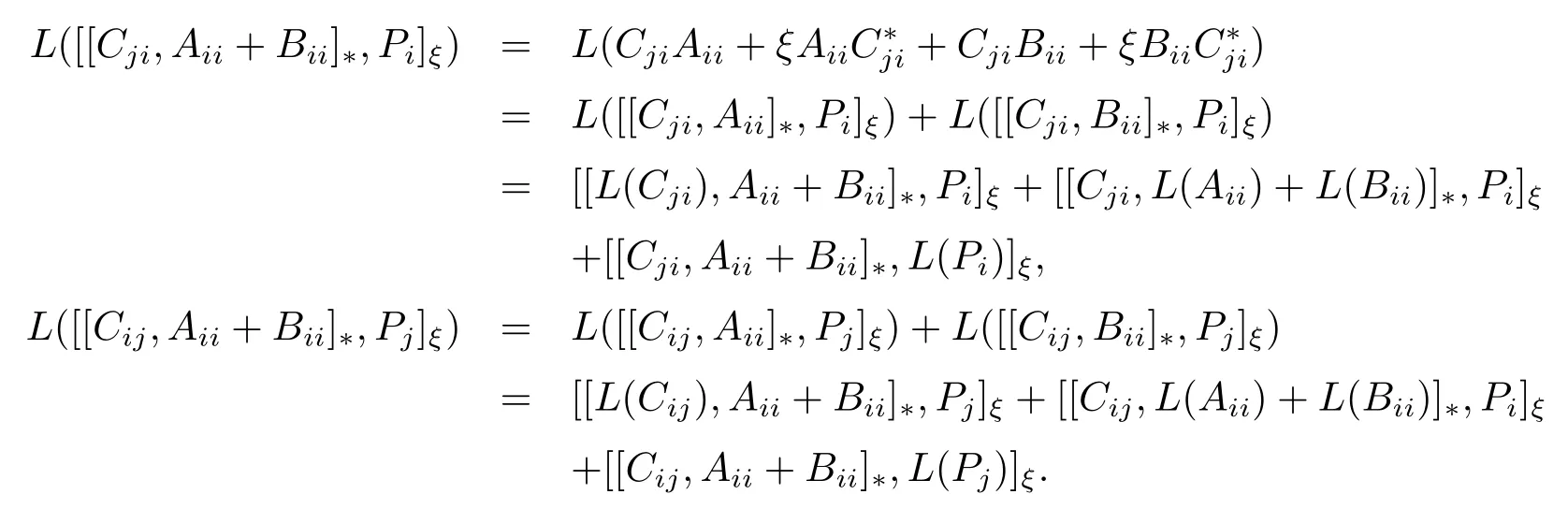
故 [[Cji,T]?,Pi]ξ= [[Cij,T]?,Pj]ξ= 0, 則可推出PiTPi=PjTPj= 0.因此T= 0.從而L(Aii+Bii)=L(Aii)+L(Bii).證畢.

定理 2.1 的證明由引理 2.2, 引理2.3 和引理 2.4 易知, 對任意的A,B ∈M, 有L(A+B)=L(A)+L(B).繼而可知L是一個可加映射.定理證畢.

3 主要結論

下面的定理便是本文最主要的結論.

定理3.1設M是一個有單位元和非平凡投影的素的?-代數,L:M →M是一個混合Lie 三重ξ- 導子且1.則L是一個可加 ? - 導子, 且對任意的A ∈M, 有L(ξA)=ξL(A).

引理3.1設A ∈M, 則

(1)L(I)=L(I)?∈(M);

(2) 若A=A?, 則有L(A)=L(A)?;

證(1) 對任意的B ∈M, 有 0 =L([[I,B]?,I]ξ) = [[L(I),B]?,I]ξ.從而對任意的B ∈M, 有 [L(I),B]?=0, 因此L(I)=L(I)?∈Z(M).

(2) 由 (1)可知對任意的A ∈M, 若A=A?, 則有 0=L([[A,I]?,I]ξ)= [[L(A),I]?,I]ξ.由此可推出 [L(A),I]?=0, 從而當A=A?時, 則有L(A)=L(A)?.

引理 3.2設A ∈M, 則L(iA)=iL(A),L(A)?=L(A?).

證設A ∈M, 則有

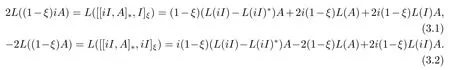
在(3.1)式和(3.2)式中, 用iA代替A后, 可得

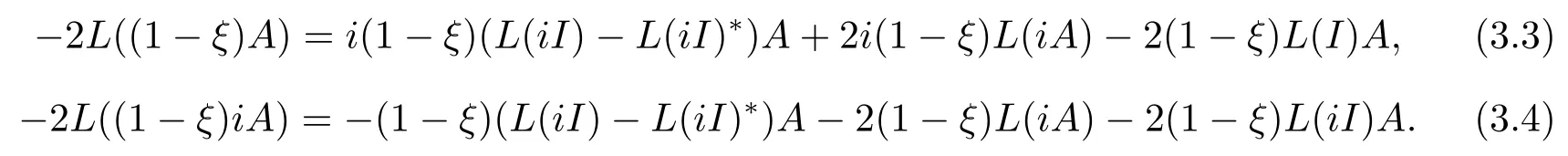
對比(3.1)式和(3.4)式以及(3.2)式和(3.3)式知, 對任意的A ∈M,有

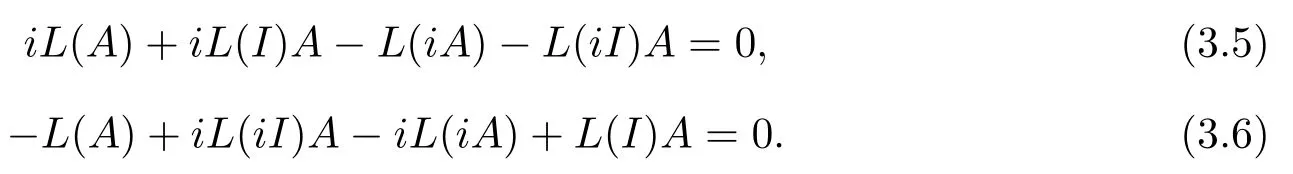
在(3.6)式等號兩側同時乘以i后有

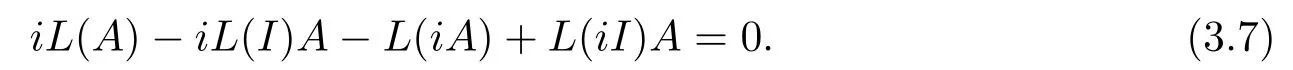
因而由(3.5)式和(3.7)式可知, 對任意的A ∈M, 有L(iA) =iL(A).根據引理3.1(2)和上式可知, 對任意的A ∈M, 均有L(A)?=L(A?).證畢.

引理3.3L ?L(I)是一個可加?- 導子.

證對任意的A ∈M, 有

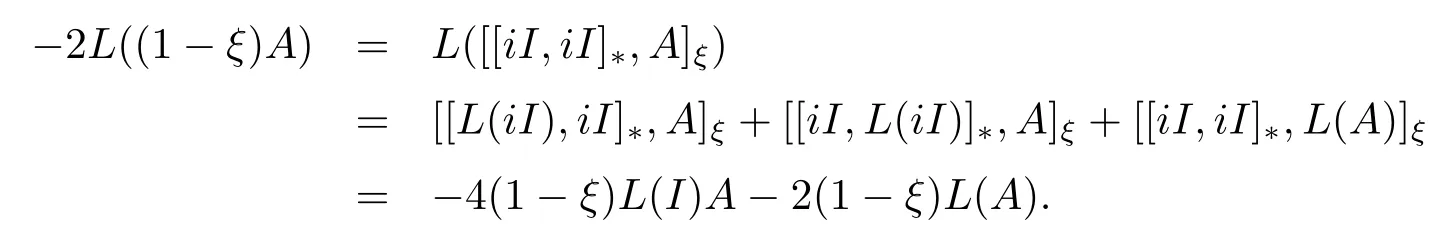
繼而有

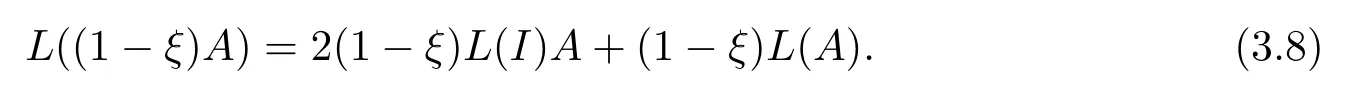
從而由(3.8)式和L是混合Lie 三重ξ- 導子可知, 對任意的A,B ∈M, 有

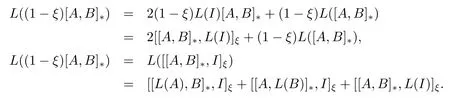
因此對任意的A,B ∈M, 有

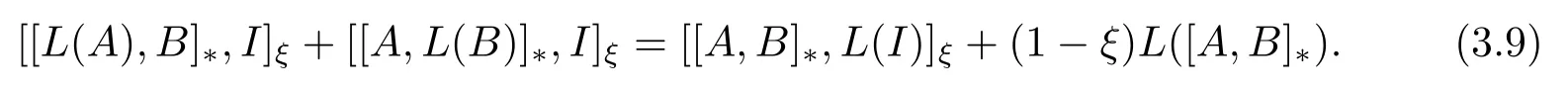
在(3.9)式中, 用iA代替A后可知, 對任意的A,B ∈M,有

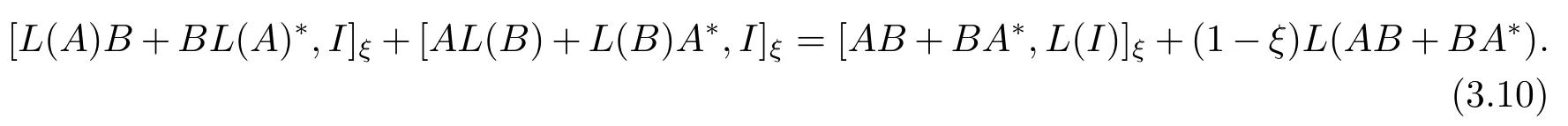
由 (3.9)式和 (3.10)式可知 [L(A)B,I]ξ+[AL(B),I]ξ=[AB,L(I)]ξ+(1?ξ)L(AB).繼而對任意的A,B ∈M, 有

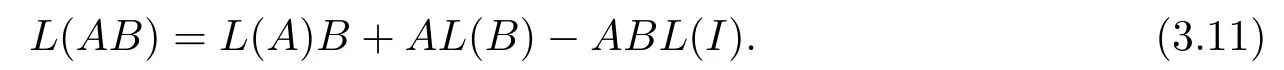
因此L ?L(I)是一個可加?- 導子.證畢.

定理3.1 的證明由引理3.3 可知, 對任意的A,B,C ∈M,有

又因

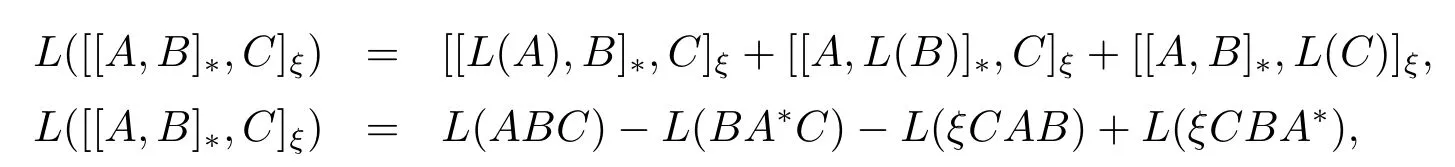
從而對任意的A,B,C ∈M,有

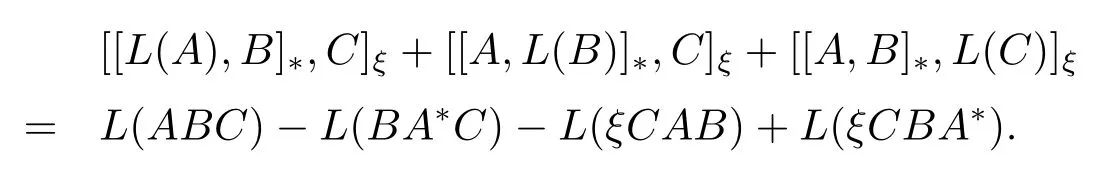
所以

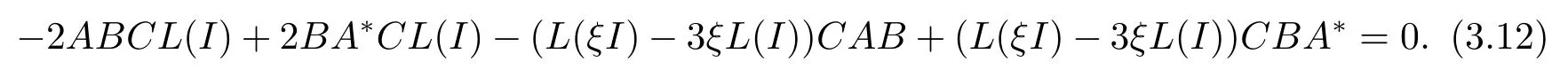
在 (3.12)式中, 令A=iI,B=C=I, 則可得 2L(I)+L(ξI)?3ξL(I)=0.因此

由 (3.12) 式和 (3.13) 式可知, 對任意的A,B,C ∈M, 有L(I)[[A,B]?,C]= 0 成立, 故L(I) =0.從而由引理2.3 可知L是一個可加的?- 導子, 且由(3.8)式可得L(ξA)=ξL(A).定理證畢.