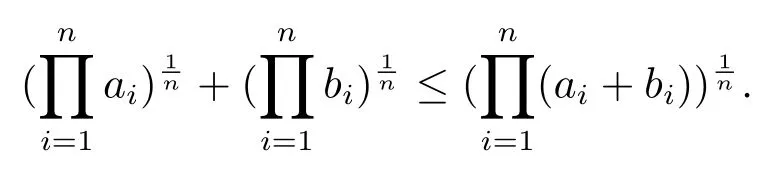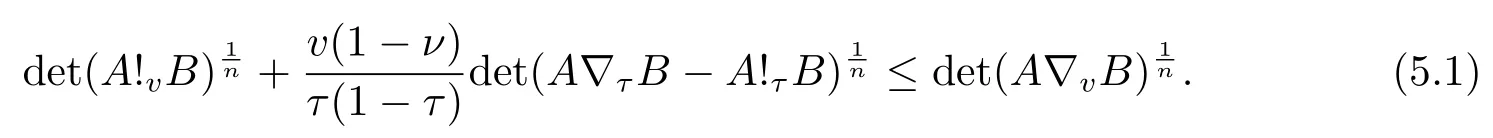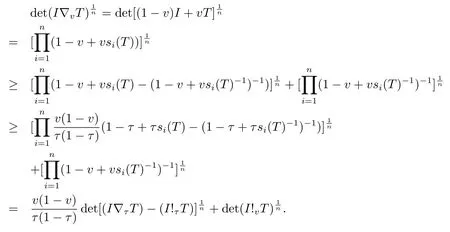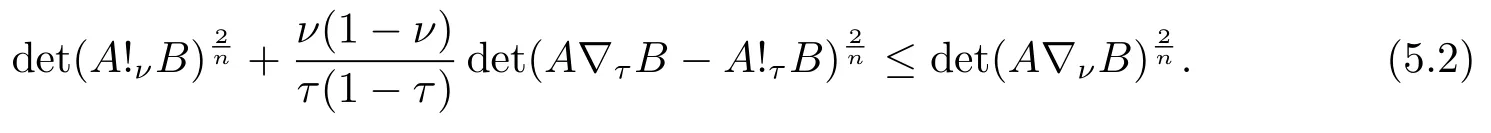IMPROVE INEQUALITIES OF ARITHMETIC-HARMONIC MEAN
YANG Chang-sen, REN Yong-hui,ZHANG Hai-xia
(College of Mathematics and Information Science, Henan Normal University,Xinxiang 453007, China.)
Abstract: We study the refinement of arithmetic-harmonic mean inequalities.First,through the classical analysis method,the scalar inequalities are obtained,and then extended to the operator cases.Specifically,we have the following main results: for 0< ν,τ <1, a,b>0 with(b?a)(τ ?ν)>0,we havewhich are generalizations of the results of W.Liao et al.
Keywords: arithmetic-harmonic mean; operator inequality; Hilbert-Schmidt norm
1 Introduction
LetMndenote the algebra of alln×ncomplex matrices,be the set of all the positive semidefinite matrices inMn.For two Hermitian matricesAandB,A ≥Bmeansis the set of all the strictly positive matrices inMn.Istands for the identity matrix.The Hilbert-Schmidt norm ofA=[aij]∈Mnis defined byIt is well-known that the Hilbert-Schmidt norm is unitarily invariant in the sense that||UAV|| =||A|| for all unitary matricesU,V ∈Mn.What’s more, we use the following notions
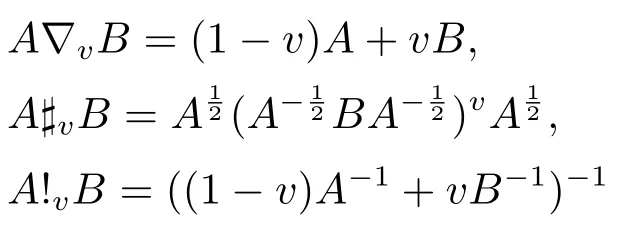
In this paper, we seta,b>0.As we all know,the scalar harmonic-geometric-arithmetic mean inequalities

hold and the second inequality is called Young inequality.Similarly,we also have the related operator version

for two strictly positive operatorsAandB.
The first refinements of Young inequality is the squared version proved in [1]
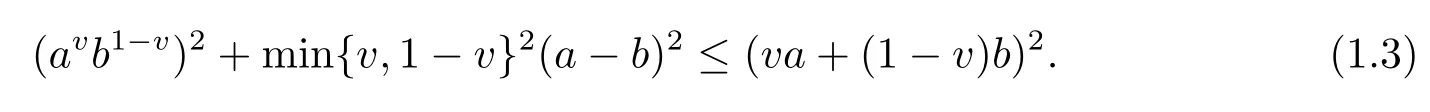
Later, authors in [2]obtained the other interesting refinement

Then many results about Young inequalities presented in recent years.wa can see [3], [4]and [5]for some related results.Also, in [3]authors proved that
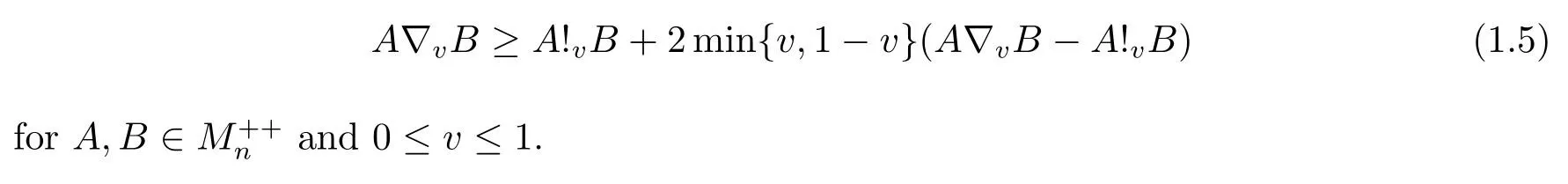
Alzer [6]proved that
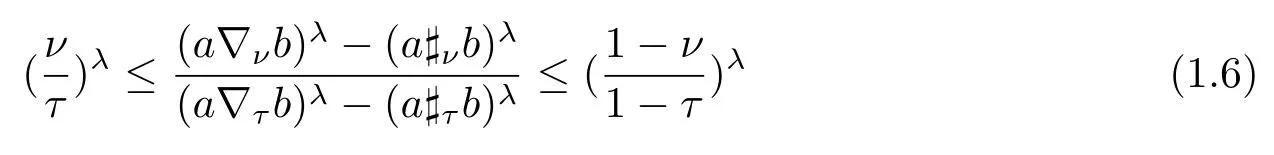
for 0<ν ≤τ<1 andλ ≥1, which is a different form of (1.5).By a similar technique, Liao[7]presented that
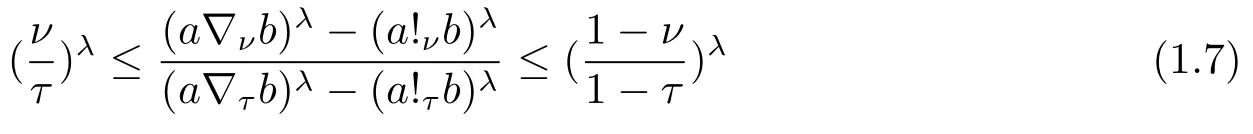
for 0<ν ≤τ< 1 andλ ≥1.Sababheh [8]generalized (1.6) and (1.7) by convexity of functionf,
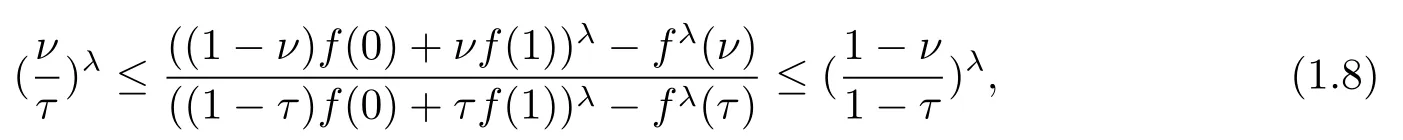
where 0<ν ≤τ<1 andλ ≥1.In the same paper [8], it is proved that

where 0<ν ≤τ<1 andλ ≥1.
Our main task of this paper is to improve (1.7) for scalar and matrix under some conditions.The article is organized in the following way: in Section 2, new refinements of harmonic-arithmetic mean are presented for scalars.In Section 3, similar inequalities for operators are presented.And the Hilbert-Schmidt norm and determinant inequalities are presented in Sections 4 and 5, respectively.
2 Inequalities for Scalars
In this part, we first give an improved version of harmonic-arithmetic mean inequality for scalar.It is also the base of this paper.
Theorem 2.1Letν,τa andbbe real positive numbers with 0<ν,τ< 1, then we have
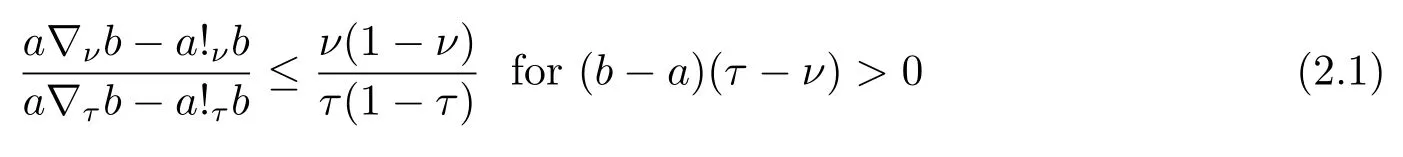
and
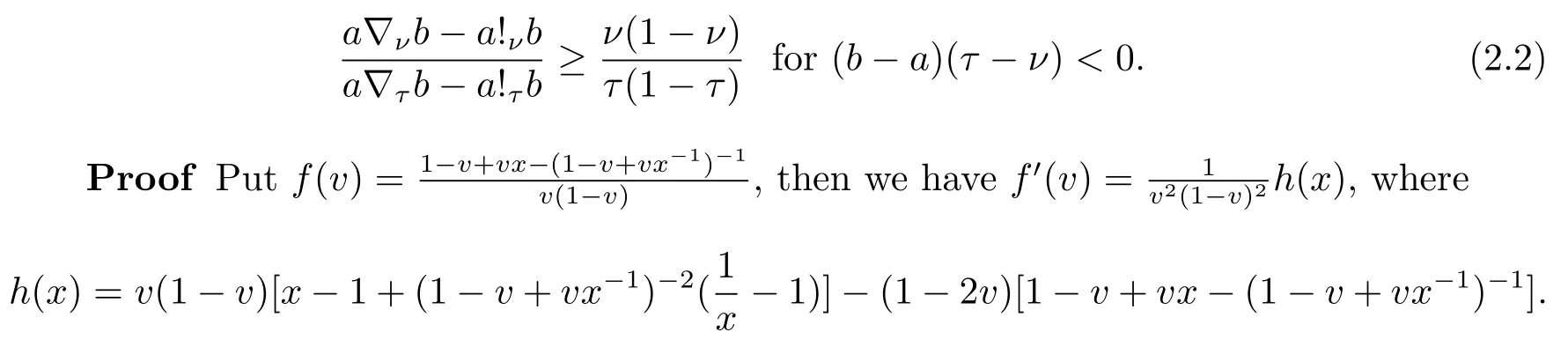
By a carefully and directly computation, we havewhereg(x) =2(1?v)(1?x)?(1?v)x?v+((1?v)x+v)3,so we can get=3(1?v)2(x?1)((1?v)x+v+1)easily.
Now if 0 Remark 2.2Let 0<ν ≤τ<1, then we have the following inequalities from (2.1), On the other hand, when 0<ν ≤τ<1 andb ?a<0, we also have by (2.1), which implies by (2.2).Therefore, it is clear that (2.3) and (2.5) are sharper than (1.7) under some conditions forλ= 1.Next, we give a quadratic refinement of Theorem 2.1, which is better than (1.7) whenλ=2. Theorem 2.3Letν,τ,aandbare real numbers with 0<ν,τ<1, then we have and by a direct computation,we havewhereg(v)=3(1?v)(1?x)?(1?v)x?v+((1?v)x+v)4.By=?4(1?x)2(1?v)[((1?v)x+v)2+1+(1?v)x+v]≤0,so we haveg(v)≥g(1)=0,which meansNow if 0 In this section, we give some refinements of harmonic-arithmetic mean for operators,which are based on inequalities (2.1) and (2.2). Lemma 3.1LetX ∈Mnbe self-adjoint and letfandgbe continuous real functions such thatf(t)≥g(t) for allt ∈Sp(X) (the spectrum ofX).Thenf(X)≥g(X). For more details about this property, readers can refer to [9]. Theorem 3.2LetA,Band 0<ν,τ<1, then for (B ?A)(τ ?ν)≥0; and for (B ?A)(τ ?ν)≤0. ProofLeta=1 in (2.1), for (b ?1)(τ ?v)≥0, then we have We may assume 0<τ Using the same technique, we can get (3.2) by (2.2).Notice that the inequalities of Theorem 3.2 provide a refinement and a reverse of (1.2). In this section, we present inequalities of Theorem 2.2 for Hilbert-Schmidt norm. Theorem 4.1LetX ∈MnandB ∈for 0 for (B ?I)(τ ?v)≥0; and for (B ?I)(τ ?v)≤0. ProofSinceBis positive definite, it follows by spectral theorem that there exist unitary matricesV ∈Mnsuch thatB=VΛV ?, where Λ = diag(ν1,ν2,···,νn) andνiare eigenvalues ofB, soνl>0,l=1,2,···,n.LetY=V ?XV=[yil], then and Now, by (2.6) and the unitarily invariant of the Hilbert-Schmidt norm, we have Here we completed the proof of (4.1).Using the same method in (2.7), we can get (4.2)easily.So we omit it. It is clear that Theorem 4.1 provids a refinement of Corollary 4.2 in [7]. Remark 4.2Theorem 4.1 is not true in general when we exchangeIforA, whereAis a positive definite matrix.That is: letX ∈MnandA,B ∈for 0<ν,τ< 1, then we can not have results as below for (B ?A)(τ ?ν)≤0. Now we give the following example to state it. Example 4.3Let(4.3) and (4.4) are not true for Proofwe can compute that and A careful calculation shows that which implies that (4.3) is not true clearly.Similarly, we can also prove that (4.4) is not true by exchangingνandτ. In this section,we present inequalities of Theorem 2.1 and Theorem 2.2 for determinant.Before it, we should recall some basic signs.The singular values of a matrixAare defined bysj(A),j= 1,2,···,n.And we denote the values of{sj(A)} as a non-increasing order.Besides, det(A) is the determinant ofA.To obtain our results, we need a following lemma. Lemma 5.1[10](Minkowski inequality) Leta= [ai],b= [bi],i= 1,2,···,nsuch thatai,biare positive real numbers.Then Equality hold if and only ifa=b. Theorem 5.2LetX ∈MnandA,B ∈for 0 ProofWe may assume 0 forj=1,2,···,n.It is a fact that the determinant of a positive definite matrix is product of its singular values, by Lemma 5.1, we have Theorem 5.3LetX ∈MnandA,B ∈for 0<ν,τ<1, then we have for (B ?A)(τ ?ν)≤0, ProofUsing the same technique above to(2.4),we can easily get the proof of Theorem 5.3.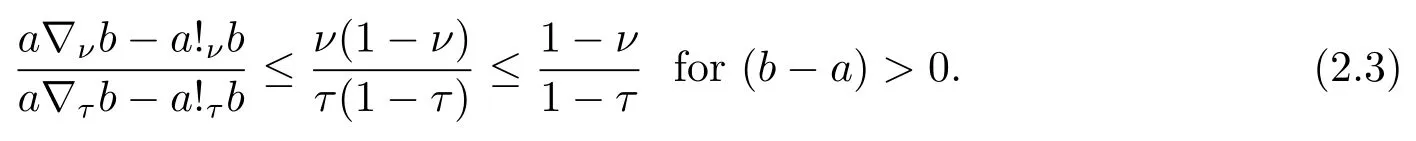
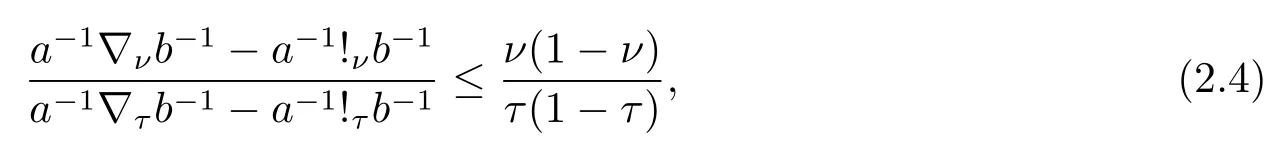
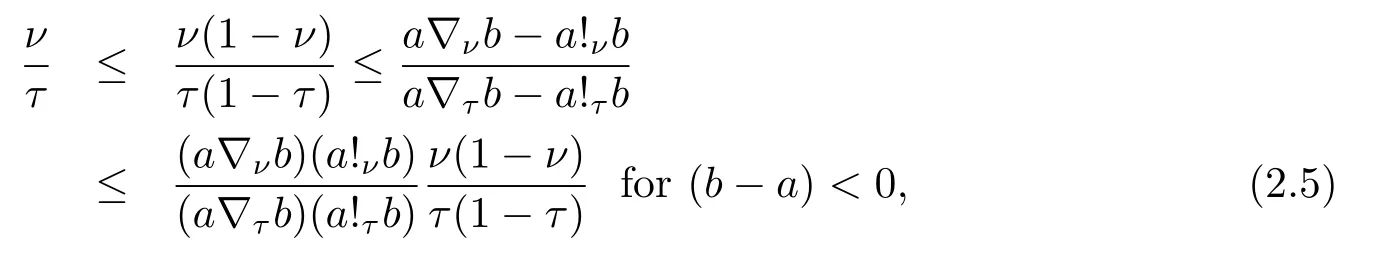
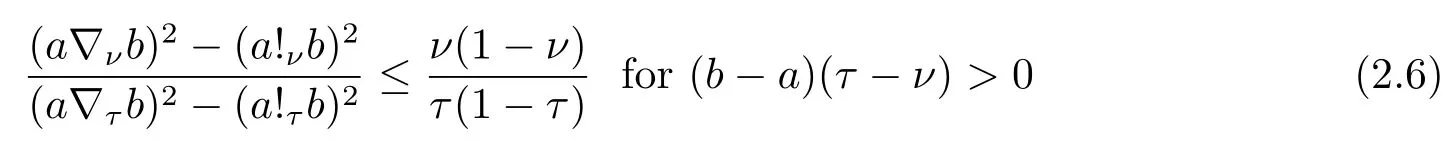
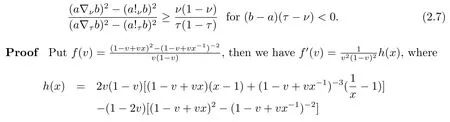
3 Inequalities for Operators
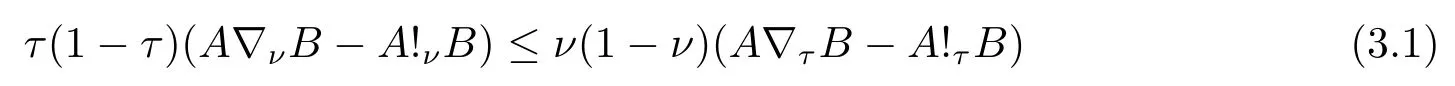
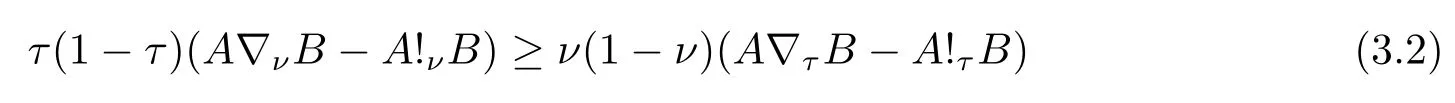
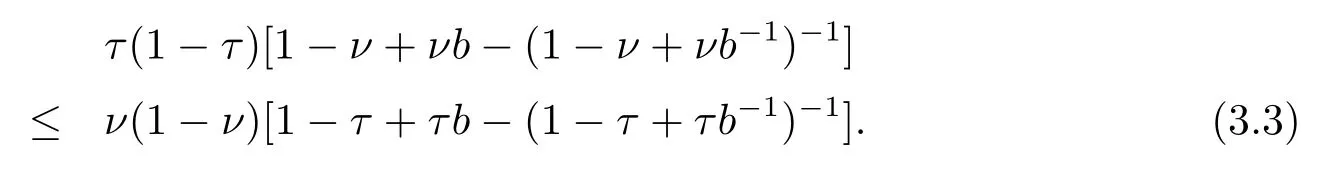
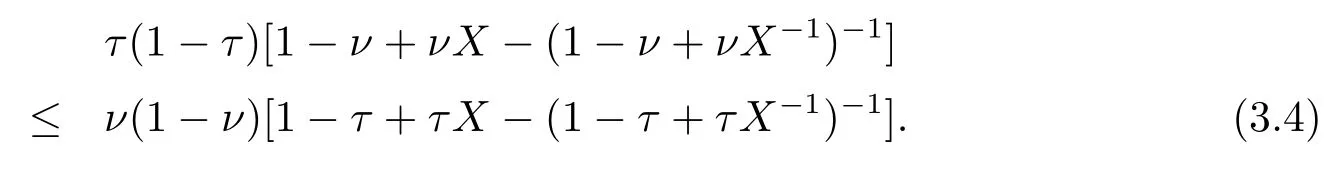
4 Inequalities for Hilbert-Schmidt Norm
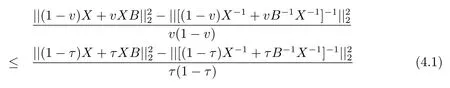
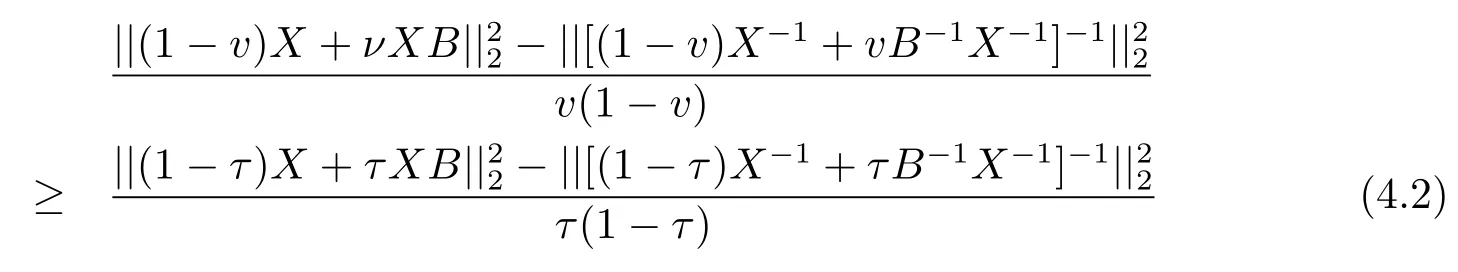
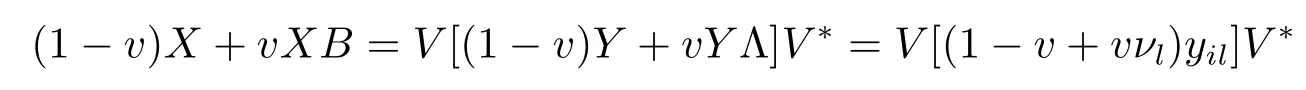
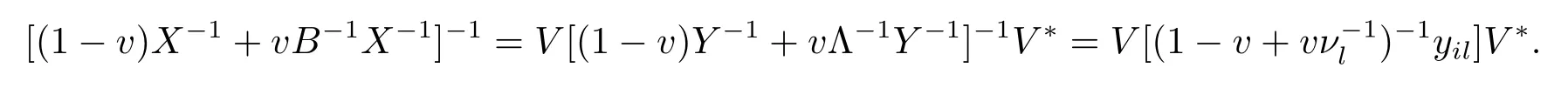
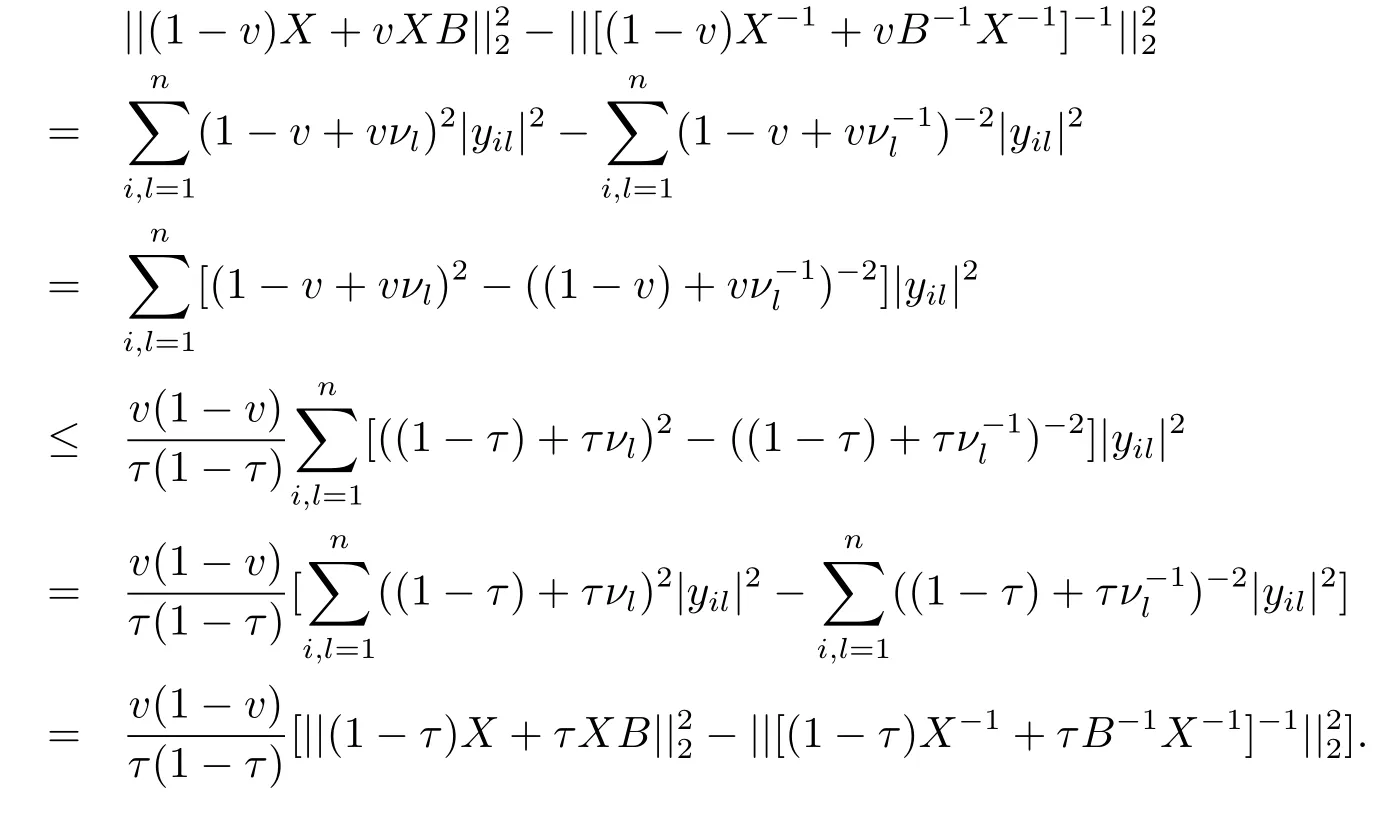

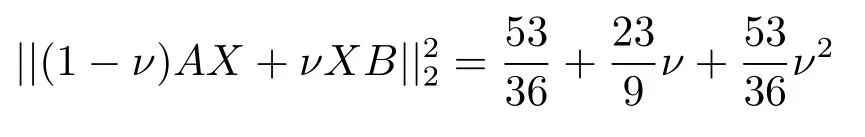
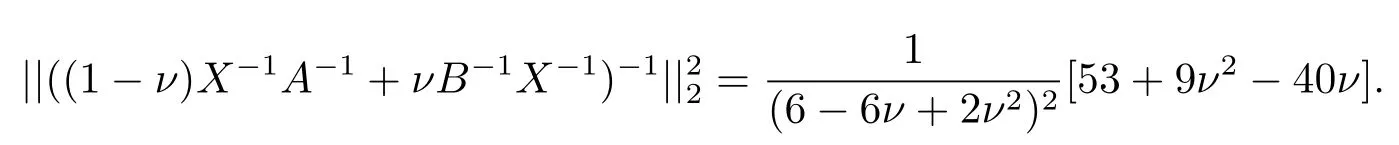

5 Inequalities for determinant