基于數據驅動的機場出租車返程方式預測模型

劉俊宇，葛振澎，李 想

(沈陽化工大學，遼寧 沈陽 110142)

隨著經濟的高速發展，國內各大機場客流量的逐漸加大。各大機場出租車拒載、宰客等不良現象時有發生。一般來說出租車送完客人到達浦東機場后，空載駛回市區成本較高，大多數就地加入排隊接客行列中[1]。但某些時刻司機在機場排隊等客時間較長，且司機并不希望從機場拉載近途乘客，一部分司機會選擇空車回城。因此，司機從機場返程時產生了進入等客區排隊載客，即載客回城和直接開空車回城到市區再拉客，即空載回城，這兩種返程方式。對出租車司機返程方式的預測將有利于對機場出租車的數量監控和調度管理。本文綜合考慮決策影響因素，引入小時客流量指數、替代物因子、氣象因子、機場出租車飽和度、空載損失度等指標在MATLAB環境下利用層次分析法構建出綜合決策權重得分模型，并通過控制限和得分的比較給出決策。

1 數據預處理

首先參考文獻[2]對上海強生公司出租車GPS 數據[3]進行速度閾值、時間閾值、空載去噪、時間降維等數據預處理并篩選出浦東機場附近的出租車坐標，數據預處理流程如圖1所示。

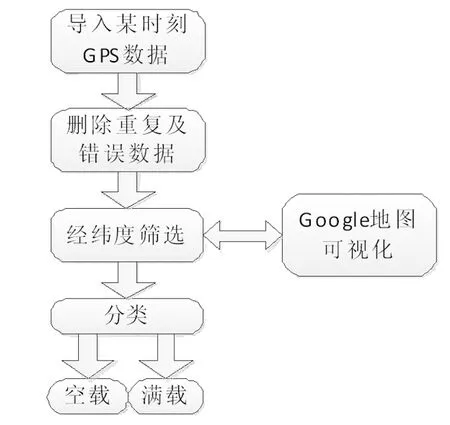
圖1 數據預處理流程圖

圖2 處理好的機場出租車GPS數據樣表

處理好的數據樣表如圖 2 所示。其列標從左到右依次代表車機號、控制字、業務狀態、載客狀態、頂燈狀態、業務狀態、無意義字段、接收日期、GPS時間經度緯度速度方向、衛星數。其中應尤為關注的是第4、12、13、14列。

提取上海市2018年4月8日12:00 和16:00浦東機場內出租車GPS數據，建立出租車分布可視化模型如圖3、4所示，其中紅色為滿載車，綠色為空載車，從圖可以看出不同時間段內機場內出租車數量和空載比變化較大。

圖3 12:00機場出租車分布

圖4 16:00機場出租車分布

2 指標定義

2.1 小時客流量指數

為簡便模型我們以機場單位時間內航班數表征機場小時客流量，并假設每個航班有50%的乘客選擇乘坐出租車。可得歸一化機場小時客流量指數：

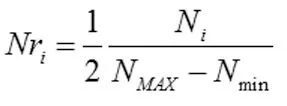
其中，Nri為小時流量指數，NMAXNmin分別為某天每小時進出港航班數的最大最小值，Ni為第i小時進出港航班數。

2.2 替代物因子

考慮到機場周邊其他交通工具對選擇乘坐出租車人數的影響，假設有25%的人選擇出租車以外的公共交通工具，可引入替代物因子Rri：

其中，Rri為第i小時的替代物因子，RMAX,Rmin分別表示第i小時內機場周邊可用公共交通工具數的最大最小值。

2.3 氣象因子

陰雨天打車人數、平均打車里程等因素會發生變化，特引入氣象因子如下：

2.4 機場出租車飽和度

將租車在“乘車區”的排隊時間對出租車司機決策的影響因素稱機場出租車飽和度飽和度：

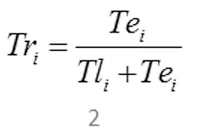
其中，Tri為出租車飽和度，Tli為載客出租車個數，Tei為空載出租車數。

2.5 空載損失度

損失度表征出租車空載回城的收益損失程度：

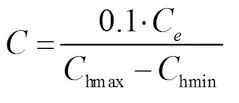
其中，Ce出租車一次載客的收益，Ch為出租車各小時最高、低收益。

其中，Ti為機場出租車小時飽和度，Tei,Tfi分別為小時機場內空車和載客出租車數，TMAX，Tmin分別為某天機場內最大最小出租車數。

3 權重模型

利用層次分析法[4]綜合考量各影響指標可得出租車決策層次模型，如圖5所示。參考Saaty等人提出的成對比較尺度在查閱大量資料和文獻后，綜合考量各成分的相對重要性后得相對比較矩陣A。

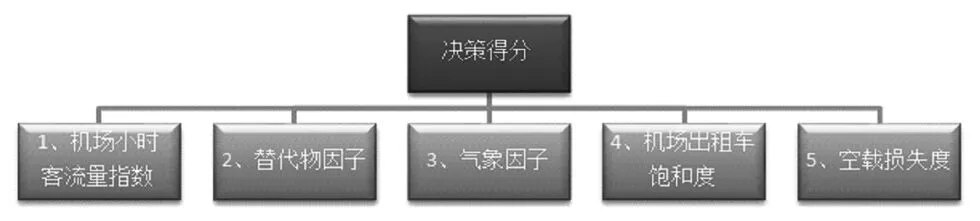
圖5 出租車決策層次模型

在MATLAB 2019a環境下運行AHP算法0.006360秒后可求得綜合權重矩陣：

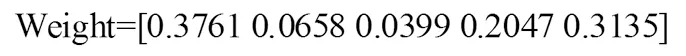
因此可得綜合決策權重模型：

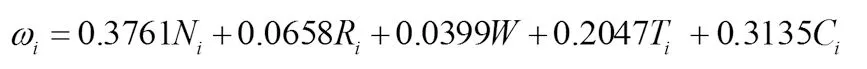
ωi表示第i小時的綜合決策指標，該值越大越應該選擇載客回城。可給出租車司機的決策方案。

4 模型求解

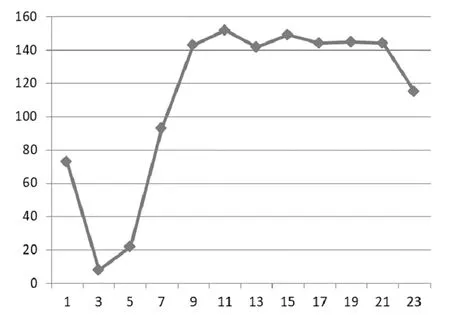
圖6 小時-機場航班數曲線

從上海市機場管理局官方網站[5]可獲得航班信息和交通情況，經過處理可得浦東機場一天(以19年5月12日為例)內航班數隨小時變化曲線如圖6。可看出凌晨0～5時航班數較少，且2～3時航班數出現波谷，8～22時航班數較多且變化較為穩定。此外，可得機場周邊可用交通工具數隨時間變化曲線(圖7)。可知5～17時交通工具數達峰值且不發生變化，3～5時和17～23時變化幅度較大。

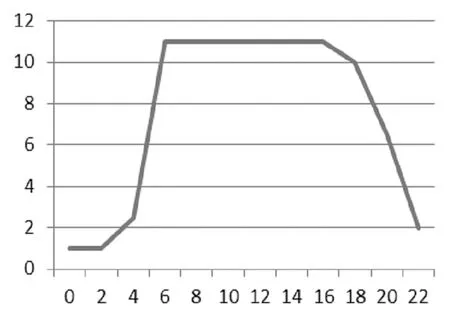
圖7 小時-機場公共交通工具數曲線

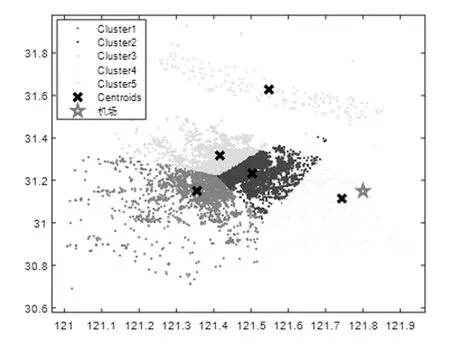
圖8 全市出租車坐標K-means聚類分析

現實生活中出租車每單收益與行駛里程存在分段函數關系。為簡便計算出租車平均收益，可以認為某時刻某點出租車密度越大出租車則越有可能前往該地，為進一步簡化模型我們使用K-means算法對出租車坐標點進行聚類分析，將區域中心坐標值代替該區域其他坐標點的坐標值。從而可以由的收益計算方法近似得到由機場載客駛出的平均收益。以12:10數據為例，代碼運行時間 0.831527 秒得聚類圖(圖8)、各區中心坐標(表1)。

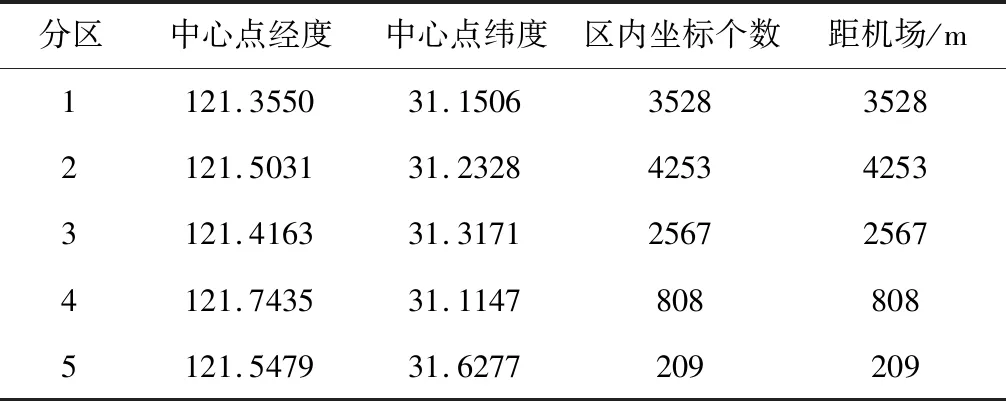
表1 各區域中心點信息表

對表1中距離對區域內坐標個數取加權平均后，帶入表的收益計算規則，可得由機場載客駛出的平均收益：

白天平均載客駛出的平均收益 (05:00-23:00)：143.5968(元)

夜間平均載客駛出的平均收益 (23:00-05:00)：186.0486(元)

由權重模型的各指標計算公式，計算出相應指標如表2(空載損失度由本問中的平均收益計算值代替)，其中出走空車比表示某時刻機場內靜止空車與運動空車的比值，可較好的表征出租車司機的實際決策情況，以此檢驗決策模型的可靠度并對控制限進劃定。

表2 各指標計算結果統計表

5 劃定控制限

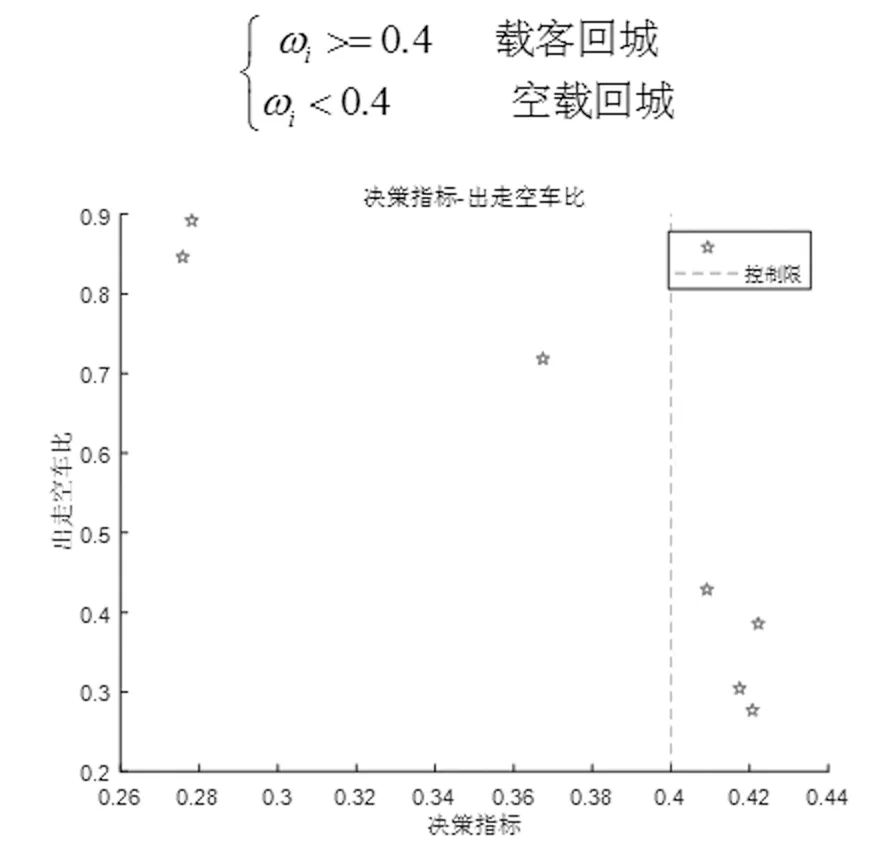
圖9 決策控制限劃定圖

由表3，可發現決策指標在0.4左右變化時出走空車比的變化幅度顯著，如對比表格第一行和第四行發現ω由0.42變化為0.36時出走空車比變化較大。因此我們將控制限擬定為0.4，如圖9所示，在控制限左側認為大部分出租車司機會選擇空車回城，在控制限右側則大部分司機會選擇客回城。

6 相關性檢驗

可使用Spss軟件求取各指標與出走空車比的相關性，其中各因子得分均較高，結果如表3所示。 再用Spss對ω與出走空車比進行了皮爾遜相關性分析，兩者線性相關性顯著如表4，這證明了模型各指標選取的合理性。

表3 各指標與出走空車比的相關性

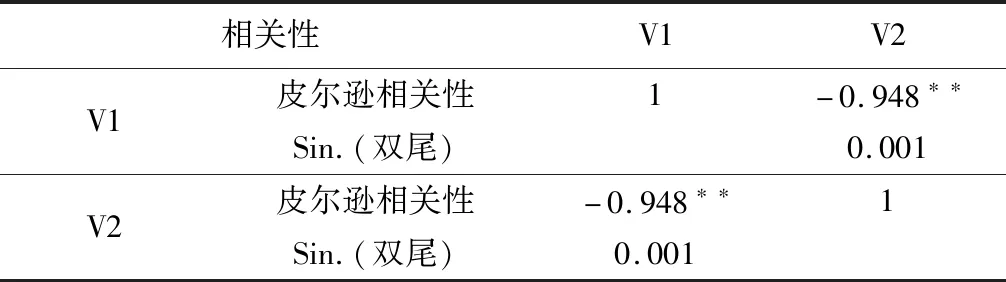
表4 ω與出走空車比的相關性

注：**，在0.01級別(雙尾)，相關性顯著。

7 總結

本文提出的是一種基于層次分析法的理想化的機場出租車返程方式預測模型，并使用Spss軟件驗證了各指標選擇的合理性。本模型只需對GPS數據進行簡單處理，運算簡便可用性強。不足之處在于抽取的樣本數過少，本文劃定的控制限僅供參考。進一步的研究可多取數據使控制限的劃定更合理。