一種衛星導航接收機固定多波束抗干擾方法

馬衍秀，馬忠志，李曉東，楊述華

(1.北京遙測技術研究所，北京 100076；2.火箭軍裝備部駐北京第二軍代表室，北京 100076)

0 引言

全球衛星導航系統(Global Navigation Satellite System, GNSS)在軍事、商業、民用基礎建設中的應用越來越廣泛。然而，由于GNSS信號到達地球表面時的功率已十分微弱，很容易受到各種有意或無意的電磁干擾，從而導致接收機接收信號的信噪比下降，定位精度降低，甚至無法捕獲跟蹤定位[1]。這也使得抗干擾技術成為了衛星導航應用領域的一個研究熱點。

自適應天線陣列是一種有效的GNSS抗干擾措施[2-4]。采用功率倒置準則的自適應調零算法已在工程實踐中得到廣泛應用。自適應調零無需任何先驗信息輔助，可通過自適應調整不同天線陣元的加權值在干擾方向形成零陷，工程實現簡單，但其在抑制干擾的同時未能對衛星信號進行有效保護，會導致衛星信號存在一定程度上的能量衰減和波形失真。為解決上述問題，進一步提升導航接收機的抗干擾能力，自適應波束形成算法成為了抗干擾技術中的一個重要研究方向[5-6]。自適應波束形成不僅能夠在干擾方向形成零陷，還通過在算法中施加衛星導向矢量約束形成指向衛星信號來向的高增益波束，在抑制干擾的同時提高衛星信號信噪比，從而對衛星信號進行有效保護。近年來，雖然自適應波束形成算法的理論研究已較為成熟，但其在工程實踐中的應用和推廣依然存在諸多問題，主要包括：1)陣列天線、射頻通道等硬件平臺的通道幅相誤差導致波束指向失配，引起抗干擾性能下降[7-8]；2)硬件平臺通道幅相誤差標定的復雜度高，對標定環境的要求較為苛刻，工程代價較大[9-11]；3)依賴載體姿態、衛星來向等先驗信息，魯棒性不高。文獻[7]分析了硬件通道幅相誤差對自適應波束形成的性能影響，指出幅相誤差可導致波束不能對準衛星信號方向、使干擾零陷深度變淺、輸出信干噪比(Signal to Interference plus Noise power Ratio, SINR)下降等問題，需要在工程設計中對幅相誤差進行校正。文獻[10]采用了一種基于真實衛星信號數據采集后處理的方法進行幅相誤差標定，但存在標定耗時長、工程可實現性差的問題。文獻[11]提出了一種基于對稱陣列單元結構設計的幅相誤差標定方法，但該方法忽略了天線陣元的安裝誤差和方向圖不圓度，工程中的標定效果很難保證。文獻[12]和文獻[13]提出了盲波束形成的抗干擾方法，但大都需要利用衛星信號的循環平穩特性或需要在干擾施加之前捕獲衛星信號，當導航接收機在強干擾環境中冷啟動時，該類方法將不能快速形成波束，影響抗干擾性能。文獻[14]提出了一種無需先驗信息的多波束抗干擾方法，但未從理論上分析最優波束的空間分配方式。

針對自適應波束形成在工程實踐中存在的問題，本文提出了一種固定多波束形成的衛星導航天線陣抗干擾方法，給出了工程實現架構，分析了最優的波束空間分配方案和衛星篩選定位策略，并通過仿真試驗進行了性能驗證。該方法無需先驗信息輔助，也無需進行復雜的幅相誤差標定，可在干擾環境中快速形成多個波束，具有抗干擾性能好、魯棒性強、易于工程實現等優點。本文安排如下：首先介紹衛星導航天線陣自適應波束形成抗干擾的信號模型，然后對本文所提出的固定波束形成抗干擾方法進行詳細的說明，最后進行仿真實驗，從而得出本文結論。

1 自適應波束形成抗干擾

考慮一個M陣元的天線陣，假設遠場有1個衛星信號s(t)和J個互不相干的干擾信號jp(t)(p=1, 2, …，J)以平面波的形式射入天線陣，則陣列接收信號X(t)可表示為

X(t)=S(t)+J(t)+N(t)

(1)

式中：S(t)、J(t)和N(t)分別為M維的衛星接收信號、干擾接收信號和本地噪聲信號；as=[a1,a2,…,aM]T為衛星信號導向矢量，與陣元位置和衛星信號來波方向有關，其中am=e-j2πf0τm(m=1,2,…,M)，τm為第m陣元接收的衛星信號與參考陣元接收的衛星信號的相對時延；同理，ap為干擾信號導向矢量。依據最小方差無失真響應(Minimum Variance Distortionless Response，MVDR)準則，如式(2)所示，將衛星信號方向增益約束為1(單位約束)，且使得陣列的輸出功率最小。

(2)

由拉格朗日乘子法，解得MVDR準則的最優權值矢量如式(3)所示

(3)

其中，Rxx=E[X(t)X(t)H]為陣列接收信號的協方差矩陣。

由式(3)可知，通過施加衛星導向矢量約束，可在抑制干擾的同時形成指向該衛星的波束，對衛星信號形成有效保護。在工程實現中，通常采用多個并行的波束形成器分別指向不同的衛星信號，典型的自適應波束形成設計架構如圖1所示。

圖1 自適應波束形成實現架構示意圖Fig.1 The structure of adaptive beamforming algorithm

衛星信號和干擾信號由天線陣接收后，經變頻和采樣，由模/數轉換模塊(A/D)將模擬信號轉換成數字中頻信號，傳遞給陣列信號處理模塊。陣列信號處理模塊通過從外界獲取衛星位置、載體姿態等先驗信息，依據MVDR準則在抑制干擾的同時對每顆衛星信號形成一個波束形成器，并分配給相應的接收機通道進行捕獲跟蹤，獲得偽碼、載波相位等信息。

理論上，自適應波束形成雖然可以進一步提升衛星導航接收機的抗干擾能力，但其在具體工程設計和應用中還存在受硬件平臺幅相誤差影響大、硬件標定復雜度高、依賴先驗信息輔助和魯棒性差等問題，這也進一步限制了自適應波束形成在某些平臺和環境中的工程應用。

2 固定多波束抗干擾

針對自適應數字波束形成在工程實現中存在的問題，本文提出了一種固定多波束形成抗干擾方法，設計架構如圖2所示。

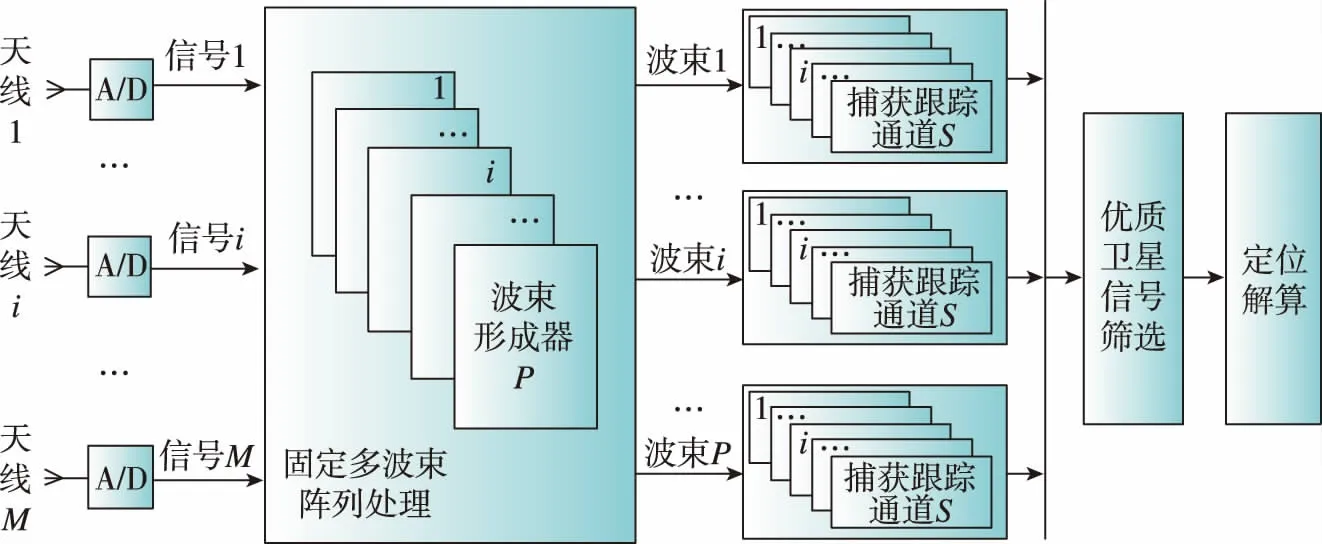
圖2 固定多波束形成實現架構示意圖Fig.2 Structure of fixed multi-beam forming algorithm

該方法的核心思想是通過將整個空域分成P個子空間，并指定P個波束形成方向，使每組權值形成的波束中的主波束指向該子空間，從而對多個衛星信號形成增益。然后通過在每個固定波束后連接捕獲跟蹤通道對衛星信號質量進行篩選，篩選后的優質衛星參與定位解算，從而得到定位結果。

與典型的自適應波束形成抗干擾方法相比，固定多波束抗干擾方法不需要載體姿態和衛星信號來向等先驗信息，也無需復雜的硬件誤差標定，接收機在冷啟動條件下也能快速形成多個波束，具有魯棒性強、更易工程實現等優點。以下分別描述固定多波束形成的最優波束分配方式和優質衛星篩選方法。

2.1 最優波束空間分配

最優波束空間分配主要從波束個數和波束增益覆蓋范圍兩方面進行考慮。設定一組波束指向初值，包括波束指向個數P和每個波束指向對應的方位角θl和俯仰角φl。如果天線陣型和每個天線單元的方向圖確定后，則該天線在每個方向上的波束覆蓋范圍是可以確定的。因此，可以根據陣列天線的陣型和各天線單元的方向圖進行波束掃描仿真，確定整個天線接收空間范圍內各方向對應的波束覆蓋范圍，從而確定波束指向個數和波束指向角度的初值。

對于陣元分布確定的天線陣列，設參考陣元的坐標為原點，第m個陣元的位置坐標為(xm,ym,zm)，m=2,…,M，當該天線陣接收來向為(θ0,φ0)的衛星信號時，所形成的數字波束方向矢量為

a=[1,ej2πf0τ2,…,ej2πf0τM]

(4)

其中，τm為第m個陣元與參考陣元接收信號之間的波程差，其解析式為

(5)

其中，c為光速，f0為信號中心頻率。

當天線陣中各陣元位置固定時，其靜態方向圖的主瓣寬度固定，由此可得該波束主瓣在方位角方向波束寬度Δθ和俯仰角方向的波束寬度Δφ。

在波束寬度Δθ和Δφ確定的情況下，可以進一步確定波束個數

(6)

其中：θmax和θmin分別為陣列天線接收空間內的最大仰角和最小仰角；φmax和φmin分別為陣列天線接收空間內的最大方位角和最小方位角。

本文以七陣元帶參考節點的圓陣為例，詳細介紹了最優多波束指向的確定。陣元位置分布如圖3所示。

仿真中，將固定波束仰角設定為20°～ 90°，方位角均設定為180°。波束的典型方向性圖分別如圖4～圖6所示，每個固定仰角的波束寬度統計如表1和表2所示。

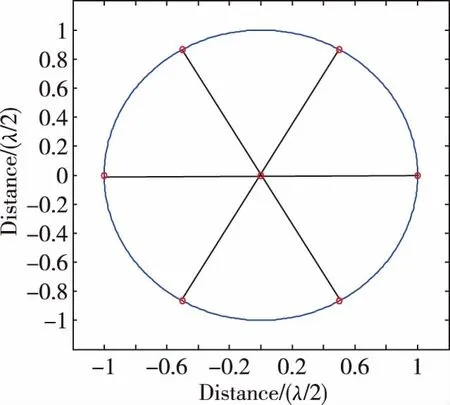
圖3 七陣元天線陣元分布示意圖Fig.3 Location of seven-array antenna array

圖4 波束指向(180°, 30°)的方向圖Fig.4 Beam pattern for (180°, 30°)

圖5 波束指向(180°, 60°)的方向圖Fig.5 Beam pattern for (180°, 60°)

圖6 波束指向(180°, 90°)的方向圖Fig.6 Beam pattern for (180°, 90°)

表1 俯仰角方向剖視波束寬度統計結果Tab.1 Statistical results of beam width after pitch angle section

表2 方向角方向剖視波束寬度統計結果Tab.2 Statistical results of beam width after yaw angle section

由表1統計結果可知，沿俯仰角剖視，在不同仰角上設定的固定波束覆蓋范圍有較大差異，波束仰角越低，波束3dB增益覆蓋的方位角范圍越小；而波束仰角越高，波束3dB增益覆蓋的方位角范圍越大。由表2統計結果可知，沿方向角剖視，當波束固定在高仰角時，波束3dB增益覆蓋90°以下至某個閾值范圍內，且仰角越高，波束3dB增益覆蓋范圍越小；當波束固定在低仰角時，3dB增益波束覆蓋0°以上至某個閾值范圍內，且仰角越小，波束3dB增益覆蓋范圍越小。波束6dB增益的覆蓋規律與3dB增益相同。

從衛星分布和抗干擾角度考慮，固定波束指向的仰角不宜過低，從波束增益覆蓋范圍角度考慮，固定波束指向的仰角不宜過高。因此，在進行固定波束分配時，可以將1個波束指向設定在高仰角90°，剩余波束指向設定在仰角30°～50°范圍，以在衛星接收空域內達到較高的波束增益覆蓋率。

本文算法設計中，設定6個固定波束，其中1個波束指向仰角90°，另外5個波束仰角均為40°，并在方位角上均勻分布，具體波束指向為(180°, 90°)、(0°,40°)、(72°,40°)、(144°,40°)、(216°,40°)、(288°,40°)。由表1和表2可知，6個固定波束的3dB增益波束覆蓋了天線陣列整個上半球空間，6dB增益可以覆蓋78.7%的上半球空間。

2.2 優質衛星信號篩選

固定多波束抗干擾將整個空域分為P個子空間，并形成P個波束，每個波束可能會覆蓋多顆衛星信號，即，抗干擾處理后P個波束的空域合集中可能含有多個重疊的衛星信號，因此需要對衛星信號進行篩選。

本文提出的方法是在捕獲跟蹤通道后增加一個衛星信號篩選模塊。模塊示意圖如圖7所示。當捕獲跟蹤到i號衛星時，首先計算該衛星的SNR

圖7 優質衛星篩選流程圖Fig.7 Flowchart of choosing high quality satellite

(7)

得到SNRnow，然后判斷當前定位解算衛星列表中是否已含i號衛星：如果列表中沒有i號衛星，則將當前捕獲跟蹤到的i號衛星添加到定位解算衛星列表，并更新SNR；否則，調出列表中i號衛星的SNRbefore，計算SNR的差值D

D=SNRnow-SNRbefore

(8)

如果D>3dB，則當前i號衛星取代原定位解算列表中的i號衛星加入定位解算衛星列表，并更新SNRbefore；否則，維持原定位解算衛星列表不變。

以6個波束子空間共收到10顆衛星為例，從6個分集中優選信噪比高的衛星進行定位解算的示意圖如圖8所示。用圓周代表波束子空間，Sn(n=1,2,3,…,12)代表收到的衛星序列號。子空間P1、P2、…、P6共收到10顆衛星，分別為

?P1：S4、S5、S6、S8；

?P2：S1、S2、S4；

?P3：S2、S3、S6；

?P4：S7、S8；

?P5：S9；

?P6：S8、S10。

圖8 各分集收星示意圖Fig.8 Schematic diagram of each diversity receiving stars

依據選星準則，S1、S3、S5、S7、S9、S10直接參與定位解算。而S2、S4、S6、S8均有2個以上(含2個)的波束收到，需要根據信噪比篩選衛星進行后續的定位解算。用Sn_Pm(n=1,2,…,10；m=1,2,…,6)表示子空間Pm收到的Sn號衛星，則最后用于定位解算的衛星為

?S1_P2、S3_P3、S5_P1、S7_P4、S9_P5、

S10_P6；

? MAX_SNR_D{S2_P2,S2_P3}；

? MAX_SNR_D{S4_P1,S4_P2}；

? MAX_SNR_D{S6_P1,S6_P3}；

? MAX_SNR_D{S8_P1,S8_P4,S8_P6}。

其中，MAX_SNR_D表示選取集合中信噪比最高且與其他衛星信噪比差值大于3dB的衛星，如不滿足D>3dB條件時，按捕獲跟蹤順序選取衛星。

3 性能仿真驗證

3.1 仿真條件

為了驗證固定多波束方法的抗干擾性能，本文采用基于MATLAB數值仿真的形式將固定多波束(Fixed Multi-Beamforming, FMB)算法與自適應調零算法(PI準則)、典型自適應波束形成算法(MVDR準則)在同一干擾環境進行了性能比較。具體仿真條件如下：

1)天線陣

天線陣沿用第2節圖3介紹的帶有中心參考陣元的七陣元圓陣，天線陣元間距滿足衛星信號半波長要求。

2)衛星信號和干擾信號

選取本地某一時刻真實的GPS可見衛星分布情況作為仿真的衛星星座條件，如圖9所示，并針對GPS L1頻點設置干擾。干擾信號為寬帶高斯噪聲干擾，中心頻點為1575.42MHz，干擾帶寬為2MHz，與衛星信號的帶寬相同。帶內熱噪聲為-140dBW，衛星信號信噪比為-20dB，干擾信號的干噪比為70dB。詳細參數設置如表3所示。

圖9 衛星和干擾位置星座示意圖Fig.9 Maps of satellite and jamming

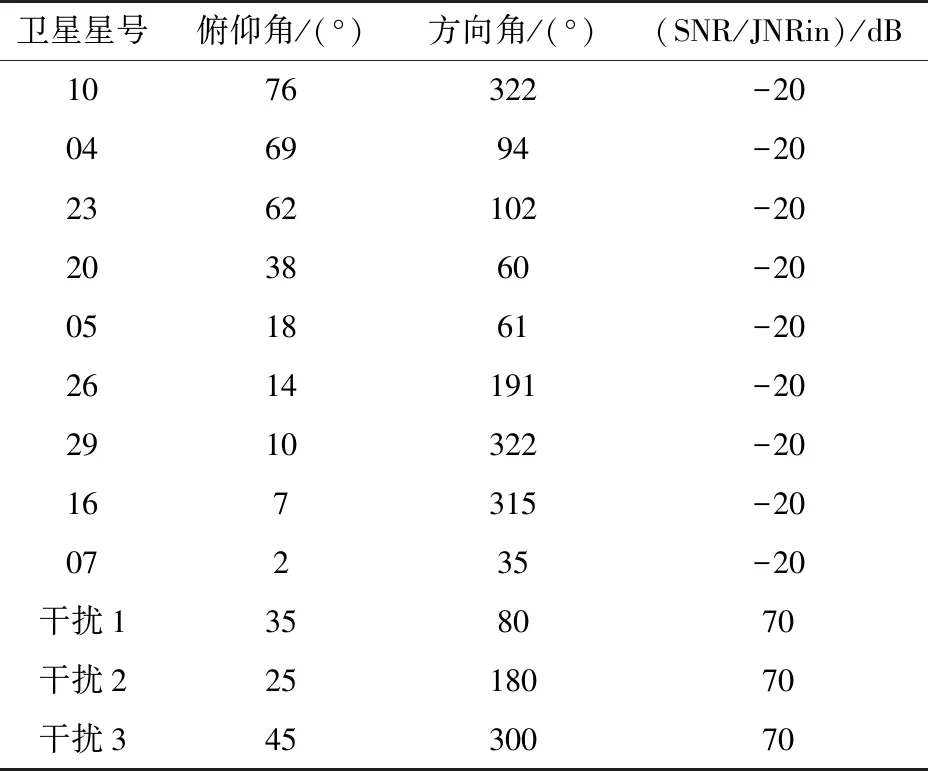
表3 衛星和干擾仿真參數設置Tab.3 Settings of satellite and jamming simulation

3)誤差項

實際硬件系統中，誤差來源主要包括陣元通道幅相誤差和ADC量化噪聲。器件發熱和老化、天線陣周圍環境的變化、陣元天線安裝誤差、濾波器群延時差異等，都會引起通道幅相特性的變化。ADC分辨率、時鐘源抖動等誤差都將產生ADC量化噪聲。因此，本文仿真中考慮硬件(陣列天線、射頻通道)通道幅相不一致誤差、ADC量化誤差和波束形成指向精度誤差。

M自適應天線陣的通道不一致系數矩陣數學模型為[1]

(9)

式中，ρi和ψi分別為第i通道的幅度誤差和相位誤差，ρi服從高斯分布，ψi服從均勻分布。對于接收天線陣列而言，其陣列流型矩陣為

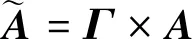
(10)

式中，A為陣列方向矢量。

相應地，天線陣的輸出則變化為[8]

X(t)=ΓΑ[S(t)+J(t)]+N(t)

(11)

式中，N(t)為通道噪聲向量。

ADC對輸入的模擬信號進行采樣和量化，定義ADC最大量化范圍為±V，量化位數為NADC，則Δ表示ADC的最小量化間隔，Δ為[14]

(12)

實際工程中，ADC的量化噪聲可以通過ADC的有效位數(ENOB)來表征。

MVDR波束指向精度誤差服從正態分布N(μ,σ2)，μ為波束指向誤差的均值，σ2為波束指向誤差分布的方差。

綜上分析，本文仿真中的誤差項參數設置為：各通道的幅度誤差在-3dB～3dB內服從高斯分布，相位誤差在-20°～20°內均勻分布；ADC量化位數為16位，有效位數為12位；MVDR波束指向精度誤差均值μ分別為5°、10°、15°和20°，方差σ2為1°。

3.2 仿真結果

分別對無誤差理想條件下和有誤差非理想條件下不同算法的抗干擾性能進行仿真，統計抗干擾處理后衛星信號的SINR。

1)理想條件

理想條件下各算法的抗干擾仿真結果如圖10所示。

圖10 理想條件下不同算法抗干擾處理后的衛星信號SINRFig.10 Comparisons of SINR after different processing

當抗干擾輸出的衛星信號SINR<-30dB時，認為接收機不能正常捕獲跟蹤到該顆衛星，因此，圖10中未畫出SINR<-30dB的衛星。從圖10中可以看出，PI算法的抗干擾性能最差，MVDR波束形成算法的抗干擾性能最好，本文提出的FMB波束形成算法與MVDR波束形成算法的性能接近。這是因為PI算法在抑制干擾的同時未對衛星信號進行有效保護，當干擾與衛星的空間分布比較接近時，PI算法對衛星信號的能量造成較大衰減。而理想條件下，MVDR波束形成算法可以將波束準確地指向各顆衛星，形成最高波束增益，從而獲得最優的抗干擾性能。FMB波束形成算法通過最優波束空間分配使波束增益覆蓋到了所有衛星，并篩選信噪比高的優質衛星參與定位解算，從而獲得接近MVDR波束形成的次優抗干擾性能。

2)非理想條件

加入硬件通道幅相不一致誤差、ADC量化噪聲誤差和MVDR波束指向精度誤差后，各算法的抗干擾仿真結果如圖11所示。

如圖11所示，在存在通道幅相誤差和波束指向精度誤差的情況下，PI算法的抗干擾性能依然最差，MVDR波束形成的抗干擾性能隨著波束指向精度誤差的增加出現下降，特別是20號星和5號星的SINR下降明顯，本文提出的FMB算法抗干擾性能無明顯下降。表4統計了MVDR波束形成算法與FMB波束形成算法抗干擾處理后輸出的同一顆衛星的SINR差值，其中，當MVDR算法處理后的衛星信號信干噪比高時，數值為正，反之為負。

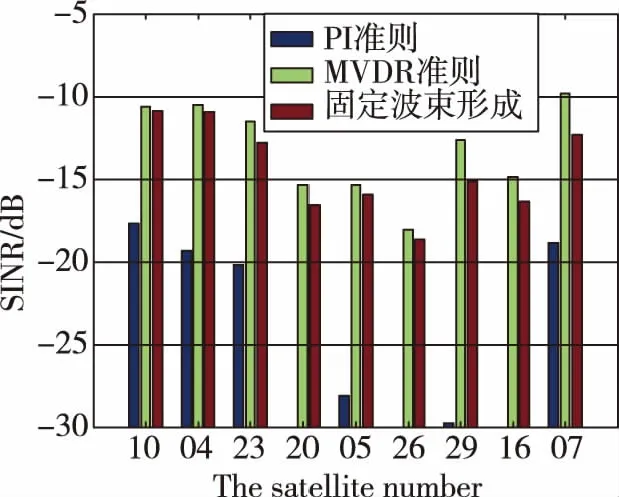
(a)波束指向精度誤差5°

(b)波束指向精度誤差10°

(c)波束指向精度誤差15°

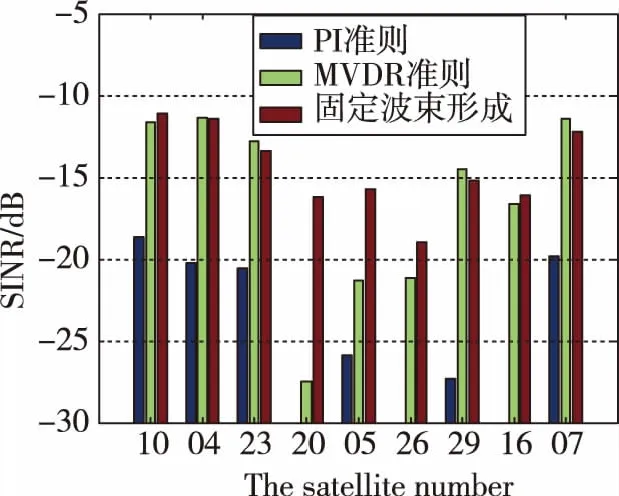
(d)波束指向精度誤差20°圖11 非理想條件下不同算法抗干擾處理后的衛星信號SINRFig.11 Comparisons of SINR after different processing

表4 不同算法處理后信號信干噪比統計表Tab.4 SNR statistical results of signal processed by different algorithms

由表4可知，在存在硬件通道幅相誤差的條件下，當波束指向精度誤差為5°時，FMB算法抗干擾輸出的衛星信號SINR與MVDR算法非常接近，兩種算法SINR差值的平均值為1.20dB；當波束指向精度誤差為10°時，兩種算法的SINR差值進一步縮小為0.77dB，且20號和5號衛星經FMB算法處理后的SINR已高于MVDR算法；當波束指向精度誤差為15°時，經FMB算法處理后，有4顆衛星的SINR高于MVDR處理結果；當波束指向精度誤差為20°時，FMB算法處理后衛星的SINR高于MVDR算法1.99dB，5顆衛星的SINR高于MVDR算法，特別是20號和5號衛星的SINR差距明顯，分別達到11dB和5dB以上。

從仿真結果可以看出，本文提出的FMB波束形成算法在通道幅相不一致誤差、ADC量化噪聲誤差和波束指向誤差存在的條件下，可以達到與典型MVDR波束形成算法相當的抗干擾性能。在波束指向精度誤差為20°的惡劣條件下，固定多波束方法的抗干擾性能更優，對SINR的性能改善最高達到11dB，平均改善1.99dB。相對于MVDR算法，FMB算法具有更好的抗干擾魯棒性，更易于工程實現。

4 結論

典型的自適應波束形成技術在工程實現中依賴衛星來向、載體姿態等先驗信息，受硬件通道幅相誤差和波束指向精度誤差的影響較大，且硬件標定復雜度高。針對這一問題，本文提出了一種固定多波束衛星導航接收機抗干擾方法，并給出了最優的波束空間分配方案和衛星篩選定位策略。該方法無需先驗信息輔助和復雜的硬件誤差標定，魯棒性強且更易工程實現。性能仿真驗證結果表明：在實際工程誤差存在的條件下，本文提出的固定多波束抗干擾方法性能與典型的自適應波束抗干擾方法性能相當。在波束指向精度誤差為20°的惡劣條件下，固定多波束方法的抗干擾性能更優，對SINR的性能改善最高達到11dB，平均改善1.99dB。