聯合連通拓撲下多無人機編隊控制

周紹磊，趙學遠，戴邵武，王帥磊

(海軍航空大學，煙臺 264001)

0 引言

近年來，由于編隊控制在各個領域具有廣泛的應用前景，已經成為了控制界內的一個極具吸引力的研究課題。基于協同控制，特別是多智能體系統一致性理論在文獻[1-6]中均取得了大量成果。受一致性理論的啟發，如何設計控制器，使其僅僅依賴于鄰居智能體信息，從而使得多智能體形成期望的編隊已經引起了廣泛的關注。

文獻[7]為二階多智能體系統設計了一致性控制器，使其在無向拓撲圖下形成期望編隊。文獻[8]解決了多無人機系統在有向通信拓撲條件下形成時變編隊的問題。上述文獻在多智能體編隊控制方面都取得了較好的成果，但是要求通信拓撲結構保持不變;而在實際系統中，由于受外界影響，拓撲結構發生變換，上述結論將不再適用。文獻[9]為多智能體系統設計了基于事件觸發函數的一致性控制器，使得多智能體系統形成了期望編隊，一致性控制器僅在事件觸發函數觸發時刻進行采樣，有效地節約了系統通信帶寬和計算資源。文獻[10]基于以上考慮，研究了多無人機系統在切換拓撲條件下的編隊控制，設計了一致性控制器，并利用線性矩陣不等式方法，給出了控制器的設計步驟，但要求每個切換拓撲圖至少包含一條有向生成樹。文獻[11]研究的問題同樣是針對有向切換拓撲，但其通信拓撲條件較文獻[10]更為嚴格，其假設所有可能的拓撲圖是強連通和平衡的。文獻[12]的研究結果表明，在無向通信拓撲條件下，無論拓撲圖如何切換，多智能體系統均能形成期望編隊。對比文獻[10]和文獻[11]，文獻[12]對多智能體系統的通信要求更為苛刻。

面對未來戰場環境，多無人機作戰將會成為重要形式，使得編隊控制成為多無人機控制領域的重要研究課題[13]。考慮若外界環境對通信拓撲影響更為明顯，導致通信拓撲在某時刻不能包含有向生成樹的情況，本文研究了在聯合連通拓撲條件下的多無人機時變編隊控制問題，進一步降低了對多無人機系統的通信要求。

1 基礎知識

1.1 符號約定

符號Rn×n和Cn×n分別表示n×n維的實矩陣和復矩陣。對于任意μ∈C，其實部表示為Re(μ)。In是n×n維的單位矩陣。對于方陣A，λ(A)表示其特征值；max{λ(A)}和min{λ(A)}分別表示矩陣A的最大和最小特征值。A?B表示矩陣A和B的Kronecker積。A>B和A≥B分別表示A-B是正定和半正定的。

1.2 圖論

智能體之間的通信有向拓撲圖表示為G=(V,E,A)，其中V={v1,v2,…,vN}為拓撲圖的節點集合，E?V×V為拓撲圖的邊集合，A=[aij]N×N為拓撲圖的具有非負元素aij的鄰接矩。aij表示節點vi和vj之間的連接權重，表示節點vi可以接收到節點vj的信息，否則aij=0。如果存在一個節點vi，從這個點出發沿著有向邊可以到達圖中的任意其他點，稱圖G包含有一個有向生成樹，該節點vi為根節點。根據連接權重aij=1將節點vi的鄰居定義為Ni∶={j∈V∶aij=1}。圖的Laplacian矩陣定義為L=[Lij]N×N，其中Lii=∑j≠iaij,Lij=-aij,i≠j。

1.3 引理

引理1[14]：圖G的Laplacian矩陣L至少有一個零特征值，其他非零特征值均具有正實部；如果有向圖G包含有一個有向生成樹，則0是L的簡單特征值，1N是其對應的右特征向量。

引理2[15]：對于圖的Laplacian矩陣L∈RN×N，那么存在一個矩陣M∈RN×N-1使得L=ME，其中E∈R(N-1)×N，其特定形式為

進一步，如果圖包含一個有向生成樹，那么矩陣M是列滿秩的,且矩陣EM的特征值是L的非零特征值，則Re(λ(EM))>0。

引理3[15]：對于在引理2中定義的矩陣EM，如果圖包含有一個有向生成樹，存在一個對稱正定矩陣Q和一個正標量參數α使得

(EM)TQ+QEM>αQ

(1)

其中，0<α<2min{Re(λ(EM))}

2 問題描述

在本文，將無人機視為一個質點，考慮由如下動力學模型描述的N架無人機構成的多無人機系統

(2)

其中，xi(t)和vi(t)分別代表在t時刻第i架無人機的位置和速度；ui(t)代表在t時刻第i架無人機的控制輸入。在本文的研究中，假設無人機在三維空間的運動相互解耦，因此為了求解方便，僅在一維空間對其進行研究，所得結論完全可以推廣至三維空間。

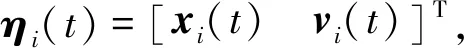
(3)

其中

ui(t) =K1(ηi(t)-hi(t))+wi(t)+

i=1,2,…,N

(4)

其中，K1、K2為待求的反饋矩陣。

定義1：多無人機系統能夠形成編隊h(t)，當且僅當

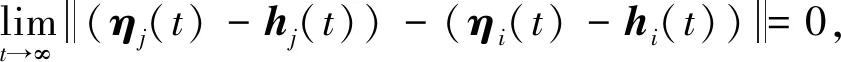
(5)

對于無人機系統(2)的任意初始狀態均成立。

本文將要研究的問題是，當無人機之間的拓撲結構為聯合連通時，在控制器(4)的作用下，如何形成期望編隊。

3 編隊分析

將控制器(4)代入系統(2)并整理可得

(Lσ(t)?BK2-IN?BK1)h(t)+

(IN?B)w(t)

(6)

令θi(t)=ηi(t)-hi(t)，可得

(IN?A)h(t)+(IN?B)w(t)-

(7)

所以

(8)

因此系統(2)的編隊控制問題轉化成了系統(7)的一致性問題

令ξi(t)=θi(t)-θi+1(t)，可得ξ(t)=Eθ(t)。

故

(E?A)h(t)+(E?B)w(t)-

(9)

因此當且僅當

(10)

且

(11)

是漸進穩定的，系統能夠形成編隊。

根據式(10)可求得

(12)

因此系統(2)的編隊控制問題等價于系統(11)的穩定性問題。

(13)

因此，將系統(11)轉化為了如下時間平均系統

(14)

由引理3可得，存在一個對稱正定矩陣Q>0和一個正定標量參數α使得

(15)

算法：如果系統通信拓撲圖切換足夠快，按照如下步驟所設計的控制器給出控制器(4)能夠使得系統(2)形成期望編隊。

1)配置(A+BK1)極點，使其極點位于負半平面，求得反饋矩陣K1；

2)根據步驟1)中求解的矩陣K1，求解線性矩陣不等式(16)，得到可行解P，進而確定K2=BTP。

(A+BK1)TP+P(A+BK1)-2αPBBTP<0

(16)

證明：構造如下Lyapunov函數

V(t)=ξ(t)T(Q?P)ξ(t)

(17)

令K2=BTP,將式(14)沿著式(11)求導可得

(18)

由式(15)可得

2αPBBTP))ξ(t)

(19)

因此根據引理4可得存在一個正常數ε*>0，使得對于任意的ε∈(0,ε*)，如下的系統是漸近穩定的

(20)

其中，ε刻畫了拓撲圖G(t/ε)的變化速度。這表明，如果拓撲切換得足夠快，系統(11)是漸進穩定的，即系統(2)在控制器(4)作用下能夠形成期望時變編隊。

4 仿真驗證

由于本文假設無人機三維運動相互解耦，故仿真時只是針對其中一維空間運動進行仿真，用以驗證所設計控制器的有效性。

設無人機的通信拓撲結構在{G1,G2,G3}中隨著時間切換，拓撲結構如圖1所示，每個通信拓撲均不包含有向生成樹，而整個拓撲集合包含一個有向生成樹。

圖1 通信拓撲圖Fig.1 Communication topology

從圖1可以看出，3個不包含有向生成樹的通信拓撲圖構成的聯合連通拓撲圖包含一條有向生成樹，其對應的Laplacian矩陣為

設無人機初始狀態為

無人機期望編隊函數

表示第i架無人機在三維空間中的期望位置，由編隊函數可知，期望編隊為4架無人機在空間中構成時變的平行四邊形。

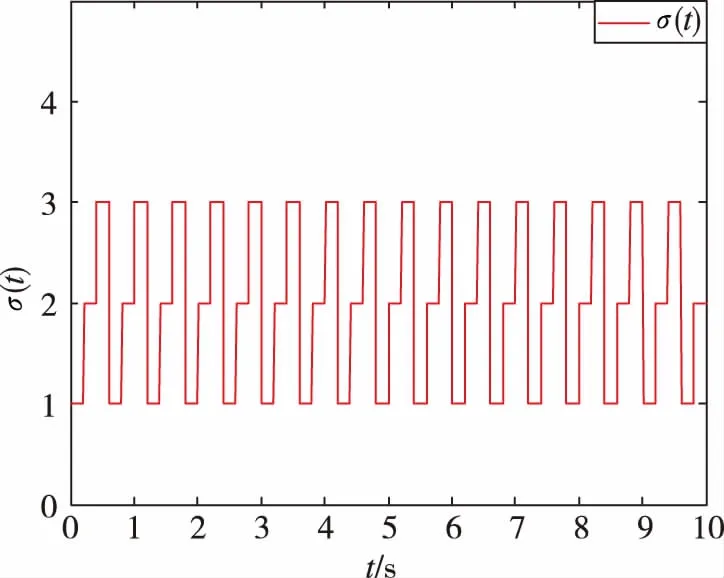
圖2 拓撲切換過程Fig.2 Topology switching process

假設無人機編隊的通信拓撲結構按照圖2所示的切換過程進行切換，即G1→G2→G3→G1→…，每個拓撲圖的駐留時間為0.2s，因此，每隔0.6s，聯合拓撲圖就包含一條有向生成樹。根據算法給出的步驟，求得反饋矩陣

當4架無人機的位置狀態與期望編隊的位置誤差達成一致時，將形成期望編隊。

圖3所示為無人機的實時位置與期望編隊函數位置誤差，從圖3中可以看出，當t=2.5s時，誤差趨于一致，意味著此時多無人機系統形成了期望編隊。

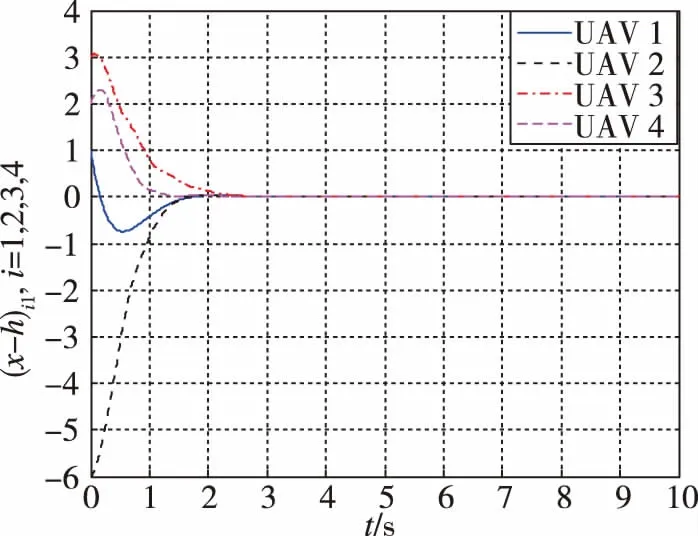
圖3 無人機與編隊函數位置誤差Fig.3 Position error of UAV and formation function

圖4和圖5分別為多無人機系統在1s和3s時，每架無人機在三維空間中的位置，每架無人機的表示符號均在圖例中給出。從圖4中可以看出，1s時多無人機系統仍未構成空間平行四邊形，即未形成期望編隊，這與圖3中1s時無人機與期望編隊函數位置誤差未達成一致。從圖5中可以看出，2.5s時，多無人機系統已經在三維空間中形成平形四邊形編隊，即達成期望編隊，與圖3中2.5s時無人機與期望編隊函數位置誤差達成一致。

圖4 1s時無人機空間位置Fig.4 Space position of UAVs at 1s

圖5 2.5s時無人機空間位置Fig.5 Space position of UAVs at 2.5s

5 結論

本文基于一致性理論，設計了一致性控制器，使得多無人機系統形成了期望編隊，得出了以下結論：

1)相比于已有結論，本文降低了多智能體系統編隊在形成過程中對通信條件的要求，降低了環境對通信的影響，同時節約了系統的通信帶寬。

2)本文通過變量代換和Laplacian矩陣的特殊分解，將編隊控制問題簡化為低階系統的漸進穩定問題，解決問題方法更為簡便。