基于多模光纖散斑的壓縮感知在光學圖像加密中的應用*

胡耀華 劉艷 穆鴿 秦齊 譚中偉 王目光 延鳳平

(北京交通大學光波技術研究所, 全光網絡與現代通信網教育部重點實驗室, 北京 100044)

為了安全高效地對圖像信息進行傳輸, 提出了一種新穎的基于多模光纖散斑的壓縮感知結合雙隨機相位編碼的光學圖像加密方法.多模光纖產生的光斑作為壓縮感知的測量矩陣, 完成對圖像的第一次壓縮和加密, 并且充當第一級密鑰; 再利用雙隨機相位編碼技術進行第二次加密, 實現對圖像的完整加密過程, 隨機相位掩模板充當第二級密鑰, 解密過程與此相反.通過將光斑測量矩陣與用于壓縮感知的常用隨機測量矩陣進行對比研究后發現, 使用光斑測量矩陣解密后的圖像質量更好, 而且相比于其他隨機測量矩陣在硬件實現上的復雜性與高成本, 光斑矩陣可以很容易地通過簡單的光學器件來獲得, 且可以利用工作波長的改變來進行變換, 也即第一級密鑰非常容易變換.同時經研究表明, 本文方法可以有效抵抗統計分析、噪聲干擾和剪切等攻擊, 且對密鑰敏感性高, 具有良好的魯棒性和安全性.因此, 本文提出的這種基于光斑矩陣的壓縮感知與雙隨機相位編碼結合起來的加密方法, 可以獲得良好的加密效果與極大的密鑰空間, 并且易于在光學領域整合.

1 引 言

隨著多媒體技術應用的飛速發展, 通信環境中需傳輸的圖像數據量日益增大, 對圖像進行壓縮和加密成為了圖像安全有效傳輸的有力保障.由于基于光學理論的信息安全技術與傳統的信息安全技術相比具有更多的優點[1], 針對圖像的加密技術目前已成為光學信息安全領域的重要研究內容之一.Refregier和Javidi最早提出了雙隨機相位編碼(double random phase encoding, DRPE)技術, 輸入圖像可在4f光學系統中轉換成平穩的白噪聲[2,3],從而實現加密.DRPE技術被提出來后受到了研究者的極大關注, 并在此基礎上展開了更進一步的研究, 提出了許多新的方法[4?7].

雖然DRPE方法在一段時間內體現了很好的優勢, 但在接下來的發展中卻遇到了各種安全問題[8?10], 特別是, 它易受到基于相位檢索技術的各種密碼分析攻擊.而產生這些安全問題的原因大多由于DRPE是線性過程, 引入壓縮感知恰好可以解決這一問題.壓縮感知是一種利用信號的稀疏性對信號進行壓縮重建的技術, 打破了傳統Nyquist?Shannon采樣定理的限制, 可極大地降低采樣的數據量[11,12].利用壓縮感知的方法在加密的同時也直接壓縮了要在信道中傳輸的圖像數據量, 因此不同于文獻[13]提出的結合壓縮過程的加密方式, 其中壓縮的意義只是選取部分有用的數據進行加密, 不會減少在信道中實際傳輸的數據量.同時, 壓縮感知的方法也不同于文獻[14]中提到的先壓縮后加密的方法, 后者所需時間會較長.

基于上述優點, 利用壓縮感知與DRPE技術結合表現出了很好的優勢[15?21].文獻[15]中提出了一種基于壓縮感知以及雙隨機相位加密的空間復用多圖像加密和解密技術, 該方法產生非線性加密系統, 能夠克服傳統DRPE的脆弱性.文獻[16]中通過在分數傅里葉變換域中采用DRPE技術和壓縮感知結合實現雙圖像加密, 除了完美的圖像重建之外, 還指出壓縮感知為傳統的DRPE系統提供了額外的安全層.與之類似的還有文獻[17], 區別在于DRPE變換域中采用了非線性分數梅林變換.而文獻[18, 19]中在上述基礎之上將得到的加密圖像嵌入到一個宿主圖像中進行信息隱藏, 但是這增加了系統的復雜性, 并且隨著嵌入強度的增大, 會減弱隱藏信息的不可感知性和安全性.文獻[20]中則將待加密圖像先分成4個塊, 然后單獨進行壓縮和加密, 每一次壓縮感知使用的測量矩陣密鑰都不相同, 這樣會大大增加算法的時間復雜度.

本文通過將壓縮感知與光學加密技術相結合,提出一種新的基于多模光纖散斑的壓縮感知光學圖像加密方案.利用多模光纖產生的光斑作為壓縮感知中的測量矩陣, 對圖像進行壓縮和第一級加密, 然后利用DRPE技術對圖像進行第二級加密,這樣兩級加密可以大大擴展密鑰空間, 使得攻擊者很難破解密鑰.通過分析證明采用這種方法加密解密時可以獲得比使用常用的隨機測量矩陣時更好的圖像質量.相比于其他測量矩陣在硬件實現上的復雜性與高成本, 光斑矩陣可以簡單地利用多模光纖而得到.而且, 由于多模光纖中模式傳輸與干涉效果對波長的敏感性, 光纖光斑將隨著光源波長的改變而改變, 因此可以非常靈活方便地通過改變光源波長來實現對基于光斑的壓縮感知中的測量矩陣進行高效更新.同時, 又由于使用多模光纖散斑的壓縮感知可以在光學域實現, 這為后續將其與DRPE技術在光學領域的整合提供了可能.研究結果表明該方案能夠大大降低圖像的采樣數據量、魯棒性好、對光斑密鑰響應敏感, 并可以抵御統計分析、噪聲污染和數據丟失等很強的攻擊.

2 理論知識

2.1 壓縮感知

壓縮感知理論指出, 當信號可在某一基下稀疏表示時能夠通過少量的測量數據對信號進行重構,大多數的圖像信號都是可以滿足這一要求的.對信號進行壓縮感知時主要包含測量和重建的兩個步驟, 假設x是長度為N的輸入信號, 測量過程可以表示為

式中Φ是M × N的測量矩陣, y是M × 1的測量值.考慮到原始輸入信號x本身一般不稀疏, 所以先將信號x稀疏表示, 于是, 壓縮感知的測量過程可進一步表示為

式中Ψ為正交稀疏基, ξ是稀疏基下的系數向量,Θ=ΦΨ被稱為傳感矩陣, 當Θ滿足受限等距性質[22]時, 能夠通過求解最優化問題高精度復原系數向量ξ, 用數學表示為：

其中 ∥ ·∥1表示L1?范數, 上述問題屬于凸優化問題,可以通過某些恢復算法來求解出系數向量ξ, 最后再恢復出原始輸入信號x.本文中所采用的恢復算法是基追蹤(basis pursuit, BP)算法.

2.2 多模光纖端面光斑圖樣

多模光纖由于其中存在的多個模式之間的干涉會在輸出端面處形成明暗不均的散斑圖樣, 即光斑圖樣, 光斑的分布情況將由多模光纖所處空間環境、光源及激發狀態等決定.將光源通過單模光纖與多模光纖偏芯連接后(如圖1所示), 當光注入到多模光纖時, 由于場的中心激發性被破壞, 因此可在多模光纖中激發出大量的非圓對稱高階傳輸模式[23], 而大量傳輸模式之間相互發生干涉就會在光纖端面處出現相比于中心激發方式更為復雜隨機的光斑圖樣.本文所用的光斑都是利用圖1所示的裝置經過實驗測得, 然后傳到計算機中做后續的仿真處理, 圖中也給出了波長為1550 nm的光對多模光纖進行偏芯激發時產生的典型光斑圖樣.

2.3 光斑矩陣的構造

在利用圖1裝置獲得合適大小的光斑圖像后對光斑圖像進行相應的處理, 使之成為后續壓縮感知中的測量矩陣, 構造過程如圖2所示.首先考慮到光斑圖像呈現出的是圓形, 而最終矩陣應該是方形, 所以先對圓形的光斑圖像進行切割, 提取其內切正方形, 接下來對內切正方形區域進行灰度轉換得到灰度圖像, 將其像素值歸一化處理后即可得到以灰度像素值為元素的N × N矩陣, 最后再根據所需要的壓縮比提取N × N矩陣中的M行即可得到壓縮感知中所需要的測量矩陣.

圖1 多模光斑產生裝置(LD, 半導體波長可調激光器; SMF, 單模光纖; MMF, 直徑為105 μm的多模光纖, 長度為5 m; IR, 近紅外相機)Fig.1.Multimode specklegram generator (LD, laser diode; SMF, single mode fiber; MMF, multimode fiber; IR, infrared camera).

圖2 光斑矩陣構造流程示意圖Fig.2.Flow chart of the construction method of the fiber specklegram based measurement matrix.

2.4 雙隨機相位編碼

DRPE技術是一種經典的加密方法, 可用4f光學系統來實現(圖3).原始待加密圖像 f (x, y) 經過輸入平面上的隨機相位掩模板(random phase mask, RPM) RPM1進行第一次調制, 然后通過透鏡進行傅里葉變換, 接著經過頻譜面上的RPM2進行調制, 最后經過透鏡進行傅里葉逆變換, 從而在輸出面上獲得類似于平穩白噪聲的加密圖像g(x, y).由于光路的可逆性, 解密是加密的逆過程.

在加密過程中, RPM1和RPM2可分別表示為

式中 ( x,y) 和 ( u,v) 分別表示空域和頻域坐標, 而a(x,y)和 b (u,v) 則分別為空域和頻域中的隨機相位函數, 它們都是在[0, 1]上均勻分布的隨機序列,對輸入光可產生0—2π的相位延遲.因此雙隨機相位加密和解密用數學過程可表示為

其中, FT表示為傅里葉變換, F T-1表示為傅里葉逆變換, *表示共軛.

圖3 基于4f的光學DRPE系統Fig.3.Optical DRPE system based on 4f.

3 加密解密方案流程圖

采用本方案對圖像進行加密解密時的流程圖如圖4所示, 首先原始圖像經過壓縮感知完成壓縮和第一次加密, 光斑充當測量矩陣和第一級密鑰,然后再用DRPE加密得到密文圖像在信道中傳輸,隨機相位板充當第二級密鑰, 在接收端實現加密的逆過程即可解密出圖像.為了驗證上述方案的可行性, 對像素大小為256 × 256的Lena圖像進行了加解密, 加解密過程中的圖像變化如圖4中A—E點所示, 可以看出解密圖像和原始圖像在視覺上很一致, 并且在加密過程中還完成了壓縮, 表明本方案是可行的.

圖4 基于多模光纖散斑的壓縮感知光學圖像加密解密過程流程圖Fig.4.Flow chart of compressive sensing optical image encryption and decryption based on multimode fiber specklegram.

4 解密效果分析

4.1 光斑矩陣與常見測量矩陣解密圖像質量對比分析

由于在進行壓縮感知時普遍使用隨機高斯矩陣等作為測量矩陣, 而本文是采用更加容易利用硬件實現的光斑矩陣作為測量矩陣, 因此本文通過與采用高斯(Gauss)矩陣、Bernoulli矩陣、Hadamard矩陣和Toeplitz矩陣的情況進行對比來衡量所提出方案的性能.為了能夠客觀地評價解密圖像的質量, 引入了峰值信噪比(peak signal to noise ratio,PSNR), 定義為

式中 M ×N 為原始圖像的大小, g (m,n) 為解密圖像, f (m,n) 為原始圖像, k表示圖像像素灰度值的位數, 通常灰度圖像的k為8, 也即有256個灰度級.圖5中特別給出了在不同壓縮比情況下采用光斑矩陣和高斯矩陣時對應的解密圖像, 另外也給出了使用其他測量矩陣時對應解密圖像的PSNR隨壓縮比的變化曲線.可以看出使用光斑測量矩陣時解密圖像質量更好.

為了更好地表明使用本方法得到的最終解密圖像的質量更優, 將本方法與文獻[15, 18, 20]進行了比較, 在相同壓縮比的情況下, 最終解密圖像的PSNR對比如表1所列.可以看出使用本方法解密出來的圖像質量是最高的.

表1 解密圖像質量分析Table 1.Decrypted image quality analysis.

圖5 光斑矩陣和高斯矩陣對比分析 (a)?(d)使用光斑矩陣在壓縮比為0.3, 0.5, 0.7, 0.9時的解密圖像; (a')?(d')使用高斯矩陣在壓縮比為0.3, 0.5, 0.7, 0.9時的解密圖像; (e)使用不同測量矩陣時對應解密圖像的PSNR隨壓縮比的變化Fig.5.Comparative analysis of specklegram matrix and Gaussian matrix：(a)?(d) The decrypted image using specklegram matrix at compression ratio of 0.3, 0.5, 0.7, 0.9; (a')?(d') the decrypted image using Gaussian matrix at compression ratio of 0.3, 0.5, 0.7, 0.9;(e) comparison between the PSNRs of the decrypted images varying with the compression ratio when using different measurement matrices.

4.2 直方圖和相關性分析

圖像中的像素間往往具有某種分布規律, 攻擊者很容易對像素進行統計分析得到圖像的有用信息.為了驗證本文方案抵抗統計攻擊的能力, 分別對3幅經典圖像分析了原始圖像和密文圖像的直方圖和相關性.如圖6所示, 第1列為原始圖像,第2列為對應的直方圖, 第3列和第4列分別為密文相位和幅值的直方圖.可以看出盡管原始圖像的直方圖非常不同, 但密文相位和幅值的直方圖在分布上彼此相似, 這表明攻擊者無法從密文的直方圖分析中獲取有用的信息.

圖6 直方圖分析 (a)原始圖像; (b)原始圖像對應的直方圖; (c)密文的相位直方圖; (d)密文的幅值直方圖Fig.6.Histogram analysis：(a) Original image; (b) histogram corresponding to original image; (c) phase histogram of ciphertext;(d) amplitude histogram of ciphertext.

圖7 相關性分析 (a)?(c)分別為明文圖像在水平、垂直和對角方向上的像素相關性分布; (d)?(f)分別為密文圖像在水平、垂直和對角方向上的像素相關性分布Fig.7.Correlation analysis：(a)?(c) Pixel correlation distributions of plaintext images in horizontal, vertical and diagonal directions;(d)?(f) pixel correlation distributions of ciphertext images in horizontal, vertical and diagonal directions.

在有意義的圖像中, 相鄰像素通常具有強相關性, 為了分析原始明文圖像和密文圖像相鄰像素的相關性, 分別從Lena明文圖像及其對應密文圖像的水平、垂直和對角方向隨機選取9000對像素進行相關性分析, 并畫出了像素的相關分布圖, 如圖7所示, 可以看出, 在水平、垂直、對角方向上, 明文圖像像素的相關性都很強, 而密文像素的相關性較弱.因此本方法可以有效地打破原有圖像像素的相關性, 對像素進行很好的擴散.

此外, 為了更直觀地表明相關性, 采用相關系數來計算源圖像和密文圖像像素在不同方向上的相關性.相關系數(correlation coefficient, CC)定義為

其中N為選取的相鄰像素對數, xi和 yi分別為兩個相鄰像素的灰度值, 不同方向上相鄰像素的相關系數如表2所列.可以看出明文圖像相鄰像素的相關系數在3個方向上都很大, 而密文圖像則很低,所以本方案的加密過程可以有效地混淆和擴散圖像像素, 因此其能夠抵抗統計分析攻擊.

此外, 也將本文方法與文獻[17, 20]中的像素相關系數進行了對比, 對于Lena圖像, 其加密后圖像像素的相關系數如表3所列.可以看出, 使用本文方法進行加密后的圖像像素相關系數要比文獻[17, 20]中的低一個數量級, 因此, 本文提出的加密方法對于擴散圖像像素具有明顯優勢.

表2 相鄰像素的相關系數Table 2.Correlation coefficient of adjacent pixels.

表3 加密圖像像素相關系數Table 3.Correlation coefficient of encrypted im?age pixels.

4.3 抗噪聲分析

考慮到密文圖像在現實通信環境中容易受到噪聲干擾, 也對本方法的抗噪聲性能進行了分析,分別對密文圖像添加均值為0, 方差為0.1到0.9的高斯白噪聲后進行解密, 圖8(a)—(d)給出了密文圖像中噪聲方差為0, 0.1, 0.3和0.5時的解密圖像, 圖8(e)為噪聲方差和解密圖像PSNR的關系圖, 可以看出加噪聲后的解密圖像與不加噪聲后的解密圖像質量基本相同, 由此可見該方案具有抗噪聲干擾的魯棒性.

4.4 抗剪切分析

還對本方法的抗剪切能力進行了分析, 分別對密文圖像從水平、垂直、中心和邊角4個方向進行不同程度的剪切攻擊, 圖9給出了受到剪切攻擊的密文圖像及其對應的解密圖像.可以看出, 解密圖像中依然能夠分辨出主要的圖像信息, 表明本方法能夠有效抵抗剪切攻擊.

圖8 抗噪聲分析 (a)?(d)在密文圖像中分別加入方差為0, 0.1, 0.3和0.5的噪聲時的解密圖像; (e)密文圖像中加入噪聲后的解密圖像PSNR隨相應噪聲方差的變化Fig.8.Anti?noise analysis：(a)?(d) Decrypted images with noise of 0, 0.1, 0.3 and 0.5 variances added to ciphertext image respect?ively; (e) curves of relationship between noise variance and the PSNR of decrypted image with noise in ciphertext mage.

圖9 水平、垂直、中心和邊角方向不同程度的剪切攻擊和剪切攻擊后的解密圖像 (a)垂直剪切10%; (b)垂直剪切50%; (c)水平剪切10%; (d)水平剪切50%; (e)中心剪切; (f)邊角剪切; (a')垂直剪切10%解密圖; (b')垂直剪切50%解密圖; (c')水平剪切10%解密圖; (d')水平剪切50%解密圖; (e')中心剪切解密圖; (f')邊角剪切解密圖Fig.9.Cropping attack of different degrees in horizontal, vertical, central, corner directions and decrypted image after cropping at?tack：(a) Vertical cropping 10%; (b) vertical cropping 50%; (c) horizontal cropping 10%; (d) horizontal cropping 50%; (e) central cropping; (f) corner cropping; (a') decrypted image after vertical cropping 10%; (b') decrypted image after vertical cropping 50%;(c') decrypted image after horizontal cropping 10%; (d') decrypted image after horizontal cropping 50%; (e') decrypted image after central cropping; (f') decrypted image after corner cropping.

4.5 光斑密鑰敏感性分析

密鑰敏感性也是加密方法的一個重要性能指標.圖10給出了原始光斑密鑰及對應的解密圖像,以及修改后的光斑密鑰及對應的解密圖像, 圖中兩個光斑是利用不同的工作波長(波長差為0.1 nm)獲得的, 可以發現從解密圖像(圖10(d))中分辨不出原始圖像的內容.為了比較解密圖像和原始圖像之間的差異, 引入了均方誤差(mean squared error,MSE), 定義為

式中 f (i,j) 和 g (i,j) 分別為原始圖像和解密圖像在位置 ( i,j) 處的像素值.使用在相同光纖結構不同波長入射光情況下實驗產生的光斑進行解密, 圖10(e)給出了MSE曲線, 圖10(f)為圖10(e)波長下對應的光斑, 波長間隔為0.1 nm.可以看出, 盡管兩光斑矩陣的工作波長相差很小, 亮斑分布方式接近,但是利用另一個光斑矩陣進行解密時, 完全無法獲得原始圖像, 只有當加密的光斑密鑰和解密的光斑密鑰來自于同一工作波長產生的光斑時, MSE數值接近于0, 其他情況下的MSE都很大, 這說明解密過程對光斑密鑰很敏感, 同時也說明通過改變光源工作波長來獲得不同密鑰的可行性.

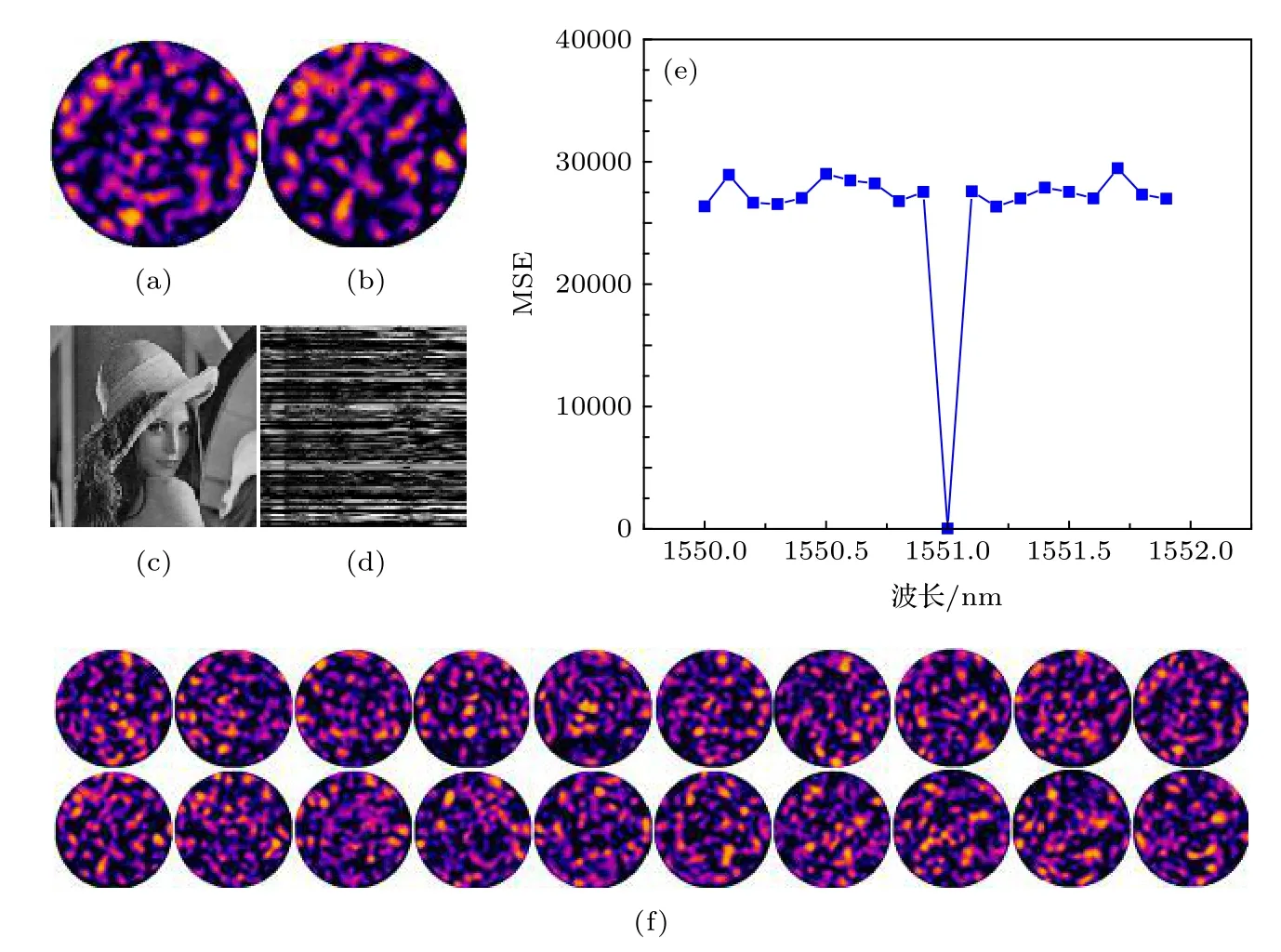
圖10 光斑密鑰敏感?性分析 (a)原始的光斑密鑰; (b)修改后的光斑密鑰; (c)與(a)相對應的解密圖像; (d)與(b)相對應的解密圖像; (e)使用15501551.9 nm (間隔為0.1 nm)工作波長產生的光斑進行解密的MSE曲線; (f)對應于(e)中使用的實驗測得的不同工作波長光斑Fig.10.Specklegram key sensitivity analysis：(a) Original specklegram key; (b) modified specklegram key; (c) decrypted image cor?responding to (a); (d) decrypted image corresponding to (b); (e) MSE curve for decryption using specklegram generated at different wavelengths; (f) the corresponding specklegram at 1550?1551.9 nm with a wavelength interval of 0.1 nm.

5 結 論

提出了一種新的基于多模光纖端面光斑的壓縮感知光學圖像加密方法, 多模光纖產生的散斑作為壓縮感知過程中的測量矩陣不僅完成了對圖像的壓縮, 還扮演著第一級密鑰的作用.隨后將壓縮感知與DRPE相結合, 成功地實現了對圖像的雙重加密.通過對光斑矩陣和常用的隨機測量矩陣用于壓縮感知并對圖像進行加密解密后的性能進行了對比分析, 發現使用光斑矩陣時解密出來的圖像質量更好, 并且在具體實現方式上, 光斑矩陣可以由非常廉價的多模光纖得到, 使得壓縮感知能夠在光學域實現, 這也為進一步將壓縮感知和DRPE在光學域的整合提供了依據.同時, 也從有效性和安全性的角度對本方案的性能進行了進一步的分析, 結果表明, 此加密方案可以打破原有圖像像素的相關性, 有效地混淆和擴散圖像像素, 有效地抵抗統計分析、噪聲污染、數據丟失等攻擊, 對密鑰的敏感性強、安全性高.而且由于可以利用不同工作波長獲得不同的光斑作為第一級密鑰, 與DRPE結合以后, 將可以獲得極大的密鑰空間.