電流連續的細導體段模型的磁場及電感*

崔翔

(華北電力大學, 新能源電力系統國家重點實驗室, 北京 102206)

傳統的載流細導體段模型是分析導體閉合回路磁場的基本模型, 盡管不滿足電流連續性定律, 但適用于導體閉合回路的磁場分析.然而, 對于工程中只關注導體閉合回路中某一局部的多分支導體段并聯的電流分配問題, 傳統模型將不能完整地反映各分支導體段之間磁場的相互作用.為此, 現有文獻提出的位移電流模型, 滿足了電流連續性定律, 較好地解決了上述問題, 但是, 仍然存在理論不完整、不自洽以及計算公式復雜等問題.本文提出載流細導體段的傳導電流模型, 確保了載流細導體段在段內、段端及段外的電流連續性.推導出物理內涵更加深刻的總磁場微分方程和矢量磁位計算公式.提出載流細導體段傳導電流模型磁場能量和電感的計算公式, 極大地降低了計算復雜度, 彌補了現有文獻的不足.本文算例從模型、公式、計算等方面驗證了本文理論和計算公式的正確性.

1 引 言

圖1 傳統的載流細導體段模型 (a) 單個載流細導體段;(b) 兩個載流細導體段Fig.1.Classical current models of filament conductor seg?ments：(a) One filament conductor segment; (b) two fila?ment conductor segments.

傳統的載流細導體段模型如圖1所示, 它是分析單個或多個導體閉合回路磁場問題的基本模型[1].盡管圖1模型不滿足電流連續性定律, 但將這些足夠短的模型依次首尾相接, 便可組成滿足電流連續性定律的導體閉合回路.因此, 圖1模型的磁感應強度及電感的計算方法, 在導體閉合回路的研究中獲得了廣泛的應用.例如, 采用圖1模型,可以推導出不同形狀的單個細導體段的自電感、不同形狀及方位的兩個細導體段的互電感等計算公式[2,3], 這些計算公式已被大量地編入各類手冊中[4?6], 并被廣泛使用.

不同于一般導體閉合回路的磁場問題, 工程中有時只關注導體閉合回路中某一局部的多分支導體段并聯的電流分配問題.例如, 圖2(a)所示的多分支導體段并聯[7]和圖2(b)所示的壓接型絕緣柵雙極型晶體管(insulated gate bipolar transistor,IGBT)器件內部多凸臺芯片并聯[8]等問題.此時,要么因這一局部的多分支導體段在整個導體閉合回路的占比極小, 要么不知其所在導體閉合回路的全部幾何參數, 如壓接型IGBT器件制造商根本不知道用戶的導體閉合回路情況等.對于這類問題,一般不再考慮導體閉合回路、而只考慮這一局部多分支導體段的磁場問題.例如, 通過提取各分支導體段的自電感和互電感, 建立圖2(c)所示的并聯支路等效電路, 以研究器件在導通或關斷瞬間總電流在各個并聯支路的分配規律等.

圖2 多導體段并聯及其等效電路 (a) 三導體段并聯[7]; (b) 壓接型IGBT器件內部多凸臺芯片并聯[8]; (c) 多導體段并聯的等效電路Fig.2.Multiconductor parallel connection and its equivalent circuit：(a) Three conductors in parallel connection[7]; (b) multi?protru?sion chips parallel connection in Press?Pack IGBTs[8]; (c) equivalent circuit for multiconductor parallel connection.

針對上述問題, 美國學者Ruehli[9]和Holloway等[10]結合導體閉合回路的電感定義, 基于采用矢量磁位表示的磁鏈法, 將導體閉合回路的電感計算公式進行分段表示, 通過引入部分電感的概念, 定義了部分電感模型.隨后, 該模型在高速電子電路、微波電路、電磁兼容等領域被廣泛采用, 開發了部分電感參數的高效提取方法和軟件[11,12].部分電感的概念還被推廣應用于頻變情況[13,14].此外,針對高速電路印制線的矩形截面導體, 美國學者Holloway和Kuester[15]推導出內電感的近似解,意大利學者Antonini等[16]研究后指出, Wheeler規則不適用矩形截面導體的內阻抗計算.

然而, 對于上述多分支導體段問題, 如果直接采用由圖1模型推導的自電感和互電感計算公式,將不能完整地反映各分支導體段之間磁場的相互作用[17].例如, 采用畢奧?薩伐爾定律推導出來的磁感應強度計算公式, 與采用安培環路定律推導出來的結果是不相同的[18].又如, 采用能量法推導出來的電感計算公式, 與采用磁鏈法推導出來的結果也是不相同的[19].導致它們不相同的根本原因在于圖1所示的載流細導體段模型不滿足電流連續性定律.

針對載流直細導體段的磁感應強度計算問題,美國學者Kalhor[18]認為, 在載流直細導體段的兩個段端上, 應該有電荷積累并在空間產生位移電流, 且位移電流應該等于載流直細導體段中的傳導電流, 以確保滿足電流連續性定律.據此, Kalhor[18,20]分別采用畢奧?薩伐爾定律與安培環路定律, 推導出來的磁感應強度計算公式是相同的, 從而解決了這個問題.

受美國學者Kalhor工作的啟發, 中國學者倪籌帷等[19,21]對圖1模型進行了修改, 提出了載流細導體段的位移電流模型, 即在載流細導體段的兩個段端添加了積累的等值但極性相反的點電荷, 并使其產生的位移電流等于載流細導體段中的傳導電流.在此基礎上, 倪籌帷等[19,21]推導出位移電流對應的矢量磁位計算公式, 論證了矢量磁位的主要性質, 進而推導出載流細導體段的自電感與互電感計算公式, 修正了現有文獻中載流細導體段的自電感與互電感計算公式的錯誤.為了進一步論證結果的正確性, 倪籌帷等[17]利用法拉第電磁感應定律,又提出了基于感應電壓的載流細導體段自電感與互電感計算公式的推導方法.從庫侖規范和洛倫茲規范兩個方面, 分析了產生矢量磁位計算出現差異的原因[19].倪籌帷等的工作在理論上解決了采用能量法與磁鏈法分別計算載流細導體段自電感與互電感的不一致問題.

然而, 倪籌帷等的工作還不夠完整.例如, 所提出的載流細導體段的位移電流模型不適用于直流情況; 又如, 矢量磁位及其規范等在理論上存在不自洽的情況; 再如, 載流細導體段的自電感與互電感計算公式沒有給出最簡單的解析表達式, 也沒有從理論上證明不同載流細導體段之間互電感的對稱性等.

針對上述問題, 本文提出了載流細導體段的傳導電流模型, 在滿足電流連續性定律的基礎上, 對磁感應強度、矢量磁位及其規范、磁場能量與電感等進行了深入的理論分析, 推導出來的細導體段自電感與互電感計算公式具有極簡單的解析形式.后面將看到, 本文提出的載流細導體段的傳導電流模型及其磁場理論, 體系完整, 電感計算公式簡單,解決了現有文獻存在的理論與計算等方面的不足.

2 載流細導體段的傳導電流模型

本文提出的載流細導體段的傳導電流模型如圖3所示, 即假設在無限大空間中充滿均勻導電媒質, i為細導體段中的傳導電流, l為細導體段的曲線段, r+為細導體段中i終止端的位置矢量,r-為起始端的位置矢量, 細導體段兩端之間的距離矢量為 d =r+-r-.假設傳導電流i隨時間變化緩慢, 其渦流效應可以忽略不計.為了分析方便, 將圖3無限大空間分為細導體段內部空間Vc和外部空間Vd.Jc為Vc中的傳導電流密度, 滿足電流連續性定律, 即

Jd為Vd中的電流密度, 也滿足電流連續性定律, 即

在細導體段的側表面Sc, 有

式中en為細導體段表面的外法向單位矢量.在細導體段的兩個段端上, 分別有

且有

不難看出, 圖3所示細導體段內部Vc中的傳導電流i, 一方面從細導體段的段端 r+流入細導體段外部Vd, 另一方面又通過細導體段的段端 r-流入到細導體段內部Vc.對于細導體段外部Vd而言, 從細導體段兩個段端流出和流入的電流可以被假設為兩個幅值相等、流向相反的點電流源.考慮到細導體段的直徑非常小, 進一步假設點電流源的電流密度對該點是球對稱均勻分布的.由疊加定理, 細導體段外部Vd中的電流密度Jd為

可以這樣解釋圖3所示的這個傳導電流模型,即在充滿均勻導電媒質的無限大空間中, 放置了一根被絕緣材料包覆的細導體段, 在細導體段內部有一個電流為i的理想電流源, 并通過細導體段的兩端向無限大空間供電.因此, 相對于現有文獻的位移電流模型而言[19,21], 這個傳導電流模型的物理圖像更加清晰, 容易被物理實現, 且適用于直流情況.

圖3 載流細導體段的傳導電流模型Fig.3.Conductive current model of filament conductor seg?ment.

3 磁感應強度

3.1 Jc產生的磁感應強度

由畢奧?薩伐爾定律, 細導體段內部Vc中電流密度Jc在場點r產生的磁感應強度Bc為

式中, μ為磁導率; eR為矢量 r -r′的單位矢量, 且R=|r-r′|.對于圖3的載流細導體段, (6a)式為

3.2 Jd產生的磁感應強度

亦由畢奧?薩伐爾定律, 細導體段外部Vd中電流密度Jd在場點r產生的磁感應強度Bd為

將(5)式代入上式, 得

為了計算 Bd, 做如下分解：

先求 Bd+(r) .為計算方便, 不妨令 r+=0 , 即讓球坐標系的原點落在圖3所示載流細導體段電流的流出端點上, 此時, (9a)式變為

在上式中, 由于 r′和r均為球坐標系的徑向位置矢量, r′× r 運算后的矢量只有 e?和 eθ分量.又由于上式積分的球對稱性, 在積分過程中 e?和eθ分量將被抵消.所以, 可以推斷, Bd+(r)=0 .可見, 盡管點電流源在無限大空間中形成傳導電流,但不產生磁場.

同理, 可以推斷, Bd-(r)=0 .所以, 由(8)式得

(10)式表明, 細導體段外部Vd中的傳導電流不產生磁場.

之所以如此, 通過上面的推導, 不難看出, 這是由于細導體段兩個端點上的點電流源各自具有球對稱性質造成的, 這種球對稱性導致細導體段外部電流密度產生的磁場因相互抵消而為零.

3.3 總磁感應強度

利用疊加定理, 細導體段內部電流密度Jc和外部電流密度Jd在空間中產生的總磁感應強度B為

將(6a)式代入(11)式, 得

3.4 B的散度與旋度

利用矢量恒等式

(12)式可以被轉換為

再利用矢量恒等式?×(φD)=(?φ)×D+φ?×D, 上式可以被寫為

式中, 由于 Jc(r′) 只是源點 r′的函數, 與場點r無關, 故等號右邊第二項為零.又因為在等號右邊第一項積分中場點r是固定的, 所以算子“ ? ”可以移到積分號外面.因此, 上式變為

利用矢量恒等式 ? ·(? × D)=0 , 對(14)式求散度, 得

再對(14)式求旋度, 得

利用矢量恒等式?×?×D=?(?·D)-?2D,上式被轉化為

下面, 分別計算(16)式等號右邊兩項積分中的被積分項.

首先, 利用矢量恒等式? ·(φD)=(?φ)·D+φ?·D, (16)式等號右邊的第一項中的被積分項可以寫為

再利用(13)式和矢量恒等式 ? ·(φD)=(?φ)·D+φ?·D, 上式可以被寫為

其次, 對于(16)式等號右邊的第二項中的被積分項, 容易證明

將(17)和(18)式代入(16)式, 并利用散度定理, 得

由本構關系 B (r)=μH(r) 和(5)式, 上式也可以寫為

式中H為總磁場強度.

可見, (15)式正是磁通連續性定律的微分形式, (19)式正是安培環路定律的微分形式.(19)式表明, 總磁場強度的旋度源由兩部分構成, 第一部分是細導體段內部Vc中的電流密度 Jc, 第二部分是為了滿足電流連續性定律而從細導體段兩個段端流出與流入的細導體段外部Vd的電流密度 Jd.

有意思的是, 盡管電流密度 Jd作為總磁場強度的旋度源之一已經體現在(19)式中了, 但正如(10)和(11)式指出的, 它并不產生磁場, 總磁場僅由細導體段內部Vc中電流密度Jc產生, 并可以直接采用畢奧?薩伐爾定律, 通過(12)式進行計算.這與美國學者Kalhor[18,20]采用位移電流假設獲得的結果是類似的.但是, Kalhor的工作是對載流直細導體段通過直接積分獲得的結果, 沒有如本文上述工作, 通過散度和旋度分析, 獲得了有更加深刻物理內涵的微分方程.

本文下節將論證, 雖然電流密度 Jd不產生磁場, 但它仍將產生矢量磁位.這一點在后面的磁場能量和電感的計算中是非常必要的.

4 矢量磁位

4.1 矢量磁位及其散度

由(15)式, 引入矢量磁位A, 即B(r)=?×A(r), 對A取庫侖規范, 即

將(19)式用矢量磁位A表示, 得

利用矢量恒等式?×?×D=?(?·D)-?2D和(20)式, 上式變為

設Ac和Ad分別為電流密度Jc和Jd產生的矢量磁位.將(21)式中的矢量磁位A做如下分解：

式中

已知(23a)式中 Ac的積分解為

為了求(23b)式中 Ad的積分解, 首先求(24)式的散度, 即

將(17)式代入上式, 并由(1a)式以及散度定理, 得

其次, 由(20)和(22)式得

再將 Ad做如下分解：

式中

為了求 Ad+(r) , 以 r+為球心做半徑為a=|r-r+|的球體.顯然, Ad+(r) 在以 r+為球心的球體上具有球對稱性, 且 Ad+(r) 是 er-r+方向的矢量.在該球體內對(28a)式進行體積分, 得

利用散度定理, (29)式等號左邊的體積分可以被轉化為

將上式與(29)式比較, 得

同理, (28b)式的解為

將(30a)和(30b)式代入(27)式, 得

再由(22)以及(24)和(31)式, 得矢量磁位A為

對于圖3的載流細導體段, (32a)式為

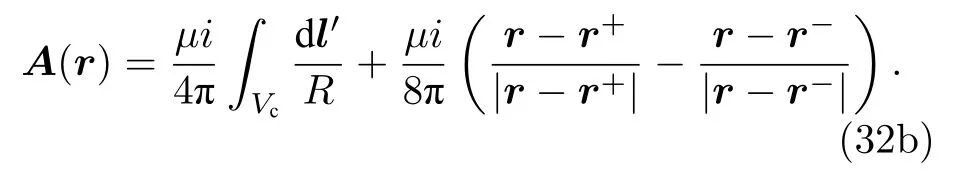
4.2 矢量磁位的旋度

首先, 求 Bc(r)=?×Ac(r) , 對(24)式兩邊取旋度得到

顯然, (33)式正是(6a)式給出的畢奧?薩伐爾定律.

其次, 求 Bd(r)=?×Ad(r) , 對 (31)式兩邊取旋度, 得

(34)式等號右邊括號內的第一項為

利用矢量恒等式 ? ×r=0 , 上式變為

同理

將(35a)和(35b)式代入(34)式, 得

(36)式再次驗證了(10)式, 即細導體段外部Vd中的傳導電流只產生(31)式中的矢量磁位 Ad,而不產生磁場.

4.3 無限遠漸近式

為了后面討論需要, 現推導當 r →∞ 時矢量磁位及其散度和旋度的漸近式.設細導體段兩個端點之間的距離為d ( d ?r ), 且距離的中點是直角坐標系或球坐標系的原點, 兩個端點均在直角坐標系的 z軸上.因此, 有

式中θ為球坐標的緯度坐標.由(24)和(33)式,當 r → ∞ 時, 有

將 (37)和 (38)式分別代入 (31)和 (26)式,當 r → ∞ 時, 有

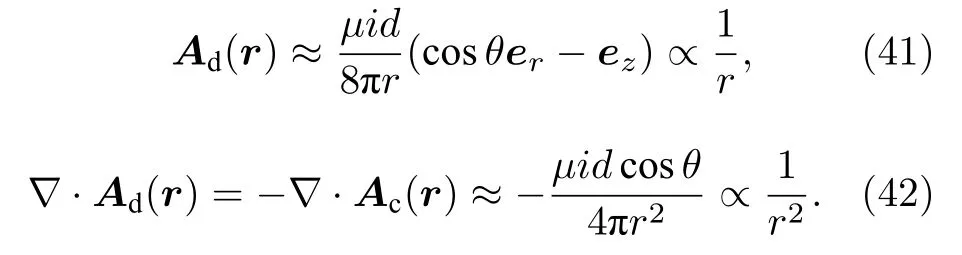
順便指出, 參考文獻[7, 19]中因錯誤地認為?·Ac(r)=0, 故導致了規范不自洽問題, 且矢量磁位的數學推導非常繁復.而本文(20)和(25)式與(26)式是自洽的, (31)式中 Ad(r) 的推導非常簡單.

5 磁場能量與電感

5.1 磁場能量

磁場能量既可以采用能量法也可以采用磁鏈法進行計算.特別是對于無限大空間的磁場問題,磁鏈法由于只需要對載流導體區域進行體積分, 因此計算量遠低于能量法.然而, 對于本文提出的載流細導體段的傳導電流模型而言, 電流充滿了整個無限大空間, 那么磁鏈法還有這種優勢嗎？現討論如下.

首先, 采用能量法計算圖3所示載流細導體段的磁場能量, 即

其次, 通過(43)式的能量法, 推導磁鏈法.

由 B (r)=μH(r) 和 B =?×A=?×Ac, (43)式被寫為

由 矢 量 恒 等 式 ?·(C × D)=(?×C)·D-C·(?×D)和?×?×D=?(?·D)-?2D, (44)式中的被積分項可以寫為

利用(26)和(23a)式以及矢量恒等式?·(φD)=(?φ)·D+φ? ·D和?×?×D=?(?·D)-?2D,上式可以被轉化為

再次利用矢量恒等式? ·(C × D)=(? × C)·D-C ·(? × D), 且由(36)式, 上式被寫為

將上式代入(44)式, 并利用散度定理, 得

由 (39)—(42)式知, 當 r → ∞ 時, 上式等號右邊的第二項面積分中的被積分項反比于 r3, 而 S∞正比于 r2, 因此該項面積分為零.因此, 上式變為

(45)式就是本文提出的計算磁場能量的磁鏈法.與現有文獻的磁鏈法被積分項僅含矢量磁位Ac不同的是, 在本文(45)式中的被積分項中, 還含有矢量磁位 Ad.正是因為現有文獻的磁鏈法中沒有這一項, 從而導致了現有文獻中細導體段的電感計算公式是不完整的.

需要指出的另外一點是, 盡管本文提出的載流細導體段的傳導電流充滿了整個無限大空間, 但是采用(45)式計算磁場能量時, 只需要對細導體段進行體積分, 不需要像(43)式中的能量法那樣, 需要對無限大空間進行體積分.顯然, (45)式極大地簡化了細導體段的磁場能量以及電感的計算復雜度.

5.2 細導體段的電感

設圖4所示的無限大空間中有兩根載流細導體段, 其中 l1和 l2分別表示沿兩根細導體段的表面路徑,分別表示沿兩根細導體段的中心路徑.下面討論電感計算問題, 包括自電感與互電感.對于載流細導體而言, 有 Jc(r′)dV′=idl′, 由(45)式的磁鏈法, 并利用(32b)式, 得磁場能量為

為了計算(46)式, 先討論(46)式等號右邊第三項和第六項的線積分, 即

式中, Amd+和 Amd-分別為第m根細導體段流出端和流入端對應的點電流源產生的矢量磁位.

對于 (47)式中 Amd+對應的線積分, 由(30a)式有

圖4 兩根細導體段Fig.4.Two filament conductor segments.

由于 d lk=drk, 因此(48)式中的線積分為

又由于a·da=0.5d(a2)=ada , 上式可以寫為

將上式代入(48)式, 得

同理, (47)式中 Amd-對應的線積分為

將(49a)和(49b)式代入(47)式, 得

如圖5所示, 設第1根和第2根細導體段的截面半徑分別為 a1和 a2, 各自流出端與流入端之間的距離分別為 d1和 d2; 第1根和第2根細導體段流出端與流入端之間的距離分別為

圖5 兩根細導體段不同端點之間的距離Fig.5.Distances between different terminals of two fila?ment conductor segments.

將(50)式代入(46)式, 并由(51)式, 得磁場能量為

采用自電感與互電感表示磁場能量, (52)式又可以寫為

將(53)式與(52)式進行對比, 得兩根細導體段的自電感與互電感分別為

將(54)式和(55)式推廣到無限大空間中具有n根細導體段的傳導電流模型, 可以得出, 第k根細導體段的自電感為

第k根細導體段與第m根細導體段的互電感為

且互電感是對稱的, 即 Lkm=Lmk.

與現有文獻的電感計算公式相比[3?6], 可以發現本文的電感計算公式(56a)和(56b)中, 分別多出了等號右邊帶方框的第二項, 即

與倪籌帷等[19,21]提出的電感計算公式相比,在本文(56)式的自電感與互電感計算公式中, 等號右邊的第二項已不再是線積分, 而是由細導體段的端點幾何參數表示的解析表達式, 且極為簡單.同時, 本文(56b)式也自然地揭示了互電感的對稱性.

6 算 例

為了說明本文提出的模型及電感計算公式的正確性, 下面引用文獻[19]的一個算例.

算例：圖6為空氣中兩根半徑相同、長度相同的圓柱形平行細導體段.細導體段半徑為r, 長度為l, 軸心距離為d, 且 d =10r .由(56a)和(56b)式,得細導體段的自電感(含內電感)和互電感分別為

需要說明的是, 式中等號右邊的兩個方框項是現有文獻中沒有的.

圖6 兩根半徑相同的圓柱截面的平行細導體段[19]Fig.6.Two parallel filament conductor segments with same length and radius[19].

圖7(a)和圖7(b)分別給出了圖6所示細導體段的單位長度自電感和單位長度互電感隨長度與半徑之比(l/r)的變化曲線.圖中藍色實線顯示的Lkk?C和Lkm?C是根據現有文獻中的電感計算公式計算的; 紅色虛線顯示的 Lkk?B和 Lkm?B是根據(43)式的能量法進行電感計算的, 即先利用畢奧?薩伐爾定律計算無限大空間的磁場, 再進行(43)式中的無限大空間積分, 最后再計算電感; 綠色帶點實線顯示的Lkk和Lkm是按本文(57a)和(57b)式進行計算的.從圖7可以看出, 對于細導體段而言, 無論是單位長度自電感還是單位長度互電感, 采用本文提出的電感計算公式獲得的結果與能量法的計算結果是一致的, 而現有文獻的計算結果因缺少(57a)和(57b)式等號右邊的兩個方框項而存在很大的誤差.

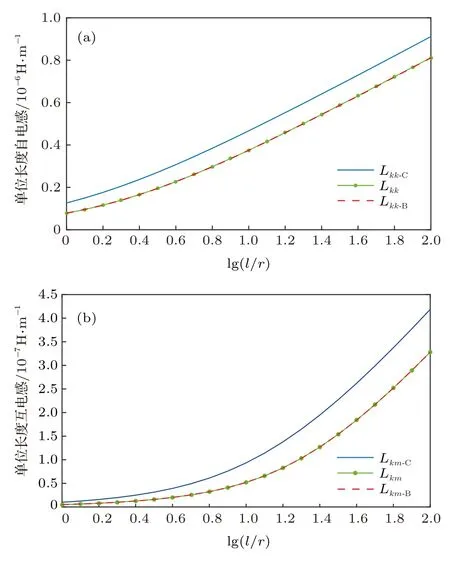
圖7 兩根平行細導體段自電感與互電感[19] (a) 單位長度自電感; (b) 單位長度互電感Fig.7.Inductances of two parallel filament conductor seg?ments[19]：(a) Unit?length self?inductance; (b) unit?length mutual?inductance.

7 結 論

本文系統地研究了細導體段的電流連續性問題, 對磁感應強度、矢量磁位及其規范、磁場能量與電感等進行了深入的理論研究.本文提出的載流細導體段的傳導電流模型及其磁場理論, 體系完整, 電感計算公式簡單, 解決了現有文獻存在的理論與計算等方面的不足, 主要結論如下.

1)提出載流細導體段的傳導電流模型, 確保了載流細導體段在段內、段端及段外的電流連續性.相對于現有文獻的位移電流模型而言, 傳導電流模型的物理圖像更加清晰, 容易被物理實現, 且適用于直流情況.

2)推導出物理內涵更加深刻的總磁場微分方程, 傳導電流模型的總磁場的旋度源包括細導體段內部和外部兩部分電流密度.由于細導體段兩個端點上的點電流源各自具有的球對稱性質, 使細導體段外部電流密度產生的磁場因相互抵消而為零, 最終導致總磁場僅由細導體段內部電流密度產生, 并可以直接采用畢奧?薩伐爾定律進行計算.

3)推導出庫侖規范下細導體段內部和外部兩部分電流密度對應的矢量磁位散度的計算公式, 解決了現有文獻中規范不自洽的問題.在此基礎上,推導出矢量磁位的計算公式, 為采用磁鏈法計算載流細導體段的磁場能量及電感奠定了理論基礎.

4)提出載流細導體段傳導電流模型計算磁場能量的磁鏈法.該法只需要對載流細導體段進行體積分, 不需要像能量法那樣對無限大空間進行體積分, 極大地降低了載流細導體段的磁場能量以及電感的計算復雜度.

5)提出細導體段自電感與互電感的計算公式,計算公式的第二項不是線積分而是由細導體段端點幾何參數表示的極為簡單的解析表達式, 論證了互電感的對稱性, 彌補了現有文獻的不足.

本文給出的算例, 進一步從模型、公式、計算等方面驗證了本文理論和計算公式的正確性.應用本文提出的細導體段電感計算公式, 可以對現有各類手冊中細導體段的電感計算公式進行進一步的修正和完善.

本文結論也適用于描述理想介質中的細導體段情況.一方面可以將理想介質認為是導電媒質的電導率趨于零的極限情況; 另一方面可以將細導體段外部Vd中的傳導電流密度Jd認為是位移電流密度, 只要保證細導體段兩個段端上的電流連續性即可.

感謝北京航空航天大學雷銀照教授的討論, 并感謝國網浙江省電力公司電力科學研究院倪籌帷博士提供的算例.