數學計算在物流應用之案例解析一

王珂達 楊莉 吉美鳳

摘? 要：我們通常接觸到的數學，一般都出現在教課書上-有時還晦澀難懂;接觸到的物流也是現實中最普通的，沒有華麗的外表;但其實兩者是有相互關聯的，數學隱含在物流中的每個角落，小到一張張條碼，大到生產產品的規劃，無一不體現數學的奧秘。利用好數學，可以讓我們更加利用好物流。

關鍵詞：數學計算、物流應用、案例解析

物流通常指物流，商量和信息流，其實信息就包含了數據，如何通過數據來挖掘信息，找到可以利用的價值，這才是數據的魅力所在，今天就讓我們用幾個案例，說明下物流中數據的應用。

案例（一）條形碼大家都不陌生，但是其中涉及的數據大家估計還不了解，我們就舉例說明其中的條碼蘊含的數學知識

我們拿1個條碼為例，9787121239472，其中總共位數為13位，最后一位為校驗碼，大家知道校驗的功能就是找出差錯，確保數據的準確無誤，如果我說蓋住其中任何1位，我可以算出蓋住的數據，估計很多人不會相信，那么我們就用一個實驗來證明給大家看看

首先計算出奇數位 7+9+2+2+7+7=34

然后算出偶數位之和4+3+1+1+8+9-=26

接著奇數位*3，34*3=102

將第2和第3步相加 26+102=128

取一個比結果大且以0為結尾的整數，相減，如130-128=2，大家發現，校驗碼正好為2，依次規律，只要知道其余的任意12個數，都可以算出其中剩余的1位數，這就是隱含在物流條碼中的數學。

具體步驟如圖

案例（二）生產物流線性規劃

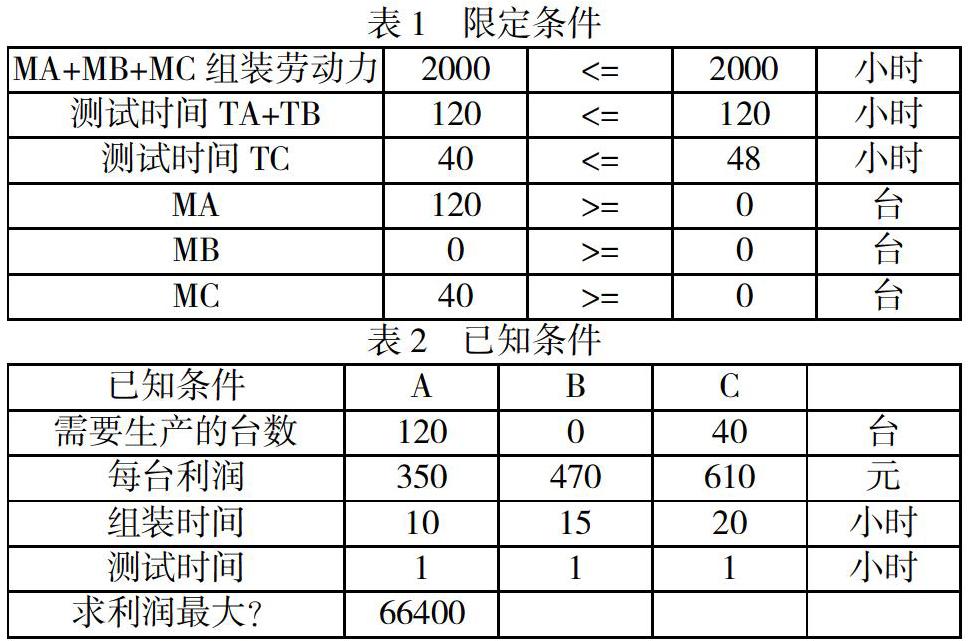
以電腦流水線為例，生產經理經常要為每周的資源分配問題而頭痛，假設公司生產三種電腦，其中分為A，B和C，電腦的銷售凈利潤分別是350元，470元和610元，其中已知凈利潤=銷售價格-直接成本;測試設備K用于測試A型和B型電腦，可用時間為120小時，測試設備L用于測試C型電腦，可用時間為48小時，每臺電腦的測試時間為1小時，可用于產品組裝的勞動力為2000小時，其中A，B，C需要組裝時間分別為10小時，15小時和20小時，如果我們是這位產品經理，該如何分配資源，達到每周利潤最大呢？

我們用MA，MB，MC分比表示表示組裝A，B和C電腦的勞動力，TA，TB和TC表示測試A，B和C電腦的時間，首先列出限定條件，如下表1所示，依據限定條件，采用EXCEL中的線性規劃，求出利潤最大值為66400元

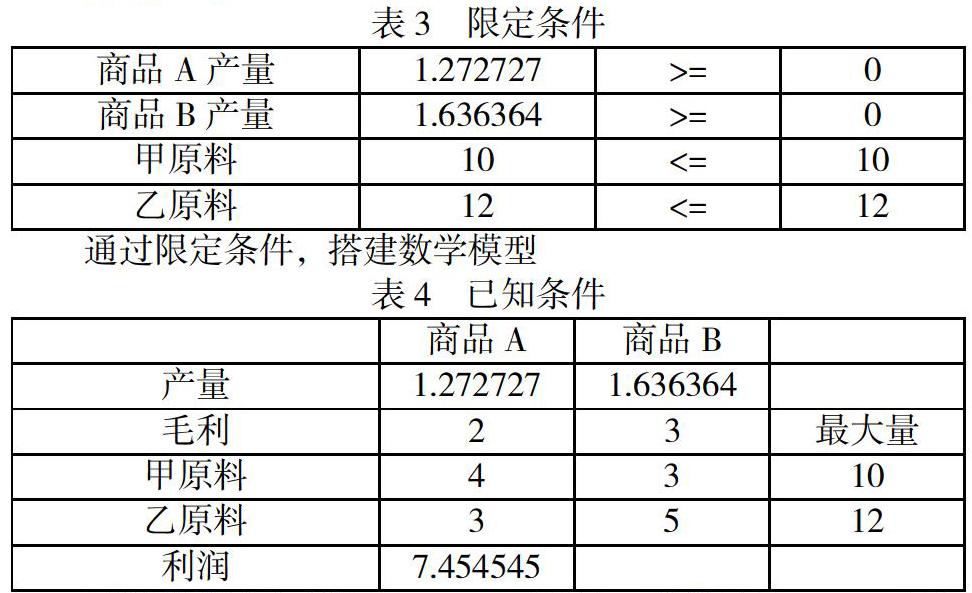
案例（三）某廠生產A，B兩種商品，銷售單位A，B商品可獲毛利分別為2與3個單位貨幣量，生產一個單位的A產品，需要消耗甲原料4個單位，乙原料3個單位，生產一個單元的B產品，需要銷售甲原料4個單位，乙原料5個單位，由于生產原料的限制，能夠提供甲乙兩種原料的最大量為10和12個單位，求A，B的產量為多少時，能夠獲得最多的銷售利潤高。

根據題意，建立模型

可以求得最大利潤為7.45，而商品A的數量為1.27，商品B的數量為1.63，此時達到利潤最大為7.454545元。

參考文獻

[1]? 曾琢. 線性規劃法在物流管理中的應用[J].中國市場2015.07

[2]? 曹亞群.數學建模在物流管理專業教學中的應用 [J].赤峰學院學報（自然科學版）2017.05

[3]? 陳宏希. 以物流管理專業為例淺談高職院校數學建模與專業學習結合.時代教育.2011.11期

作者簡介：王珂達（1976-6），男，漢族，湖南長沙人，碩士，湖南現代物流職業技術學院，研究方向：物流信息技術。