PROPERTIES ON MEROMORPHIC SOLUTIONS OF COMPOSITE FUNCTIONAL-DIFFERENTIAL EQUATIONS?
School of Mathematics,Shandong University,Jinan 250100,China
E-mail:lml6641@163.com
Lingyun GAO?
Department of Mathematics,Jinan University,Guangzhou 510632,China
E-mail:tgaoly@jnu.edu.cn
Abstract With the aid of Nevanlinna value distribution theory,differential equation theory and difference equation theory,we estimate the non-integrated counting function of meromorphic solutions on composite functional-differential equations under proper conditions.We also get the form of meromorphic solutions on a type of system of composite functional equations.Examples are constructed to show that our results are accurate.
Key words Meromorphic solution;composite functional-differential equations;?-difference
1 Introduction and Main Results
Recently,with the establishment of the difference analogues of Nevanlinna value distribution theory,researchers obtained many interesting theorems about the existence and growth of solutions of difference equations,functional equations,and so on([1,2,9–12,14,18]).We shall assume that the reader is familiar with the standard notations and results of Nevanlinna value distribution theory,such as m(r,f),n(r,f),N(r,f),and T(r,f)([13,16,20])denote the proximity function,the non-integrated counting function,the counting function and the characteristic function of f,respectively.For the growth order of f,we use the notation ρ(f),which is defined by
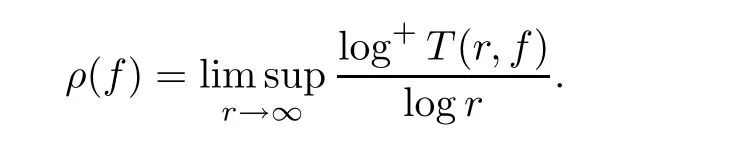
In this article,a meromorphic function means meromorphic in the whole complex plane.Given a meromorphic function f,recall that a meromorphic function h is said to be a small function of f,if T(r,h)=S(r,f),where S(r,f)is used to denote any quantity that satisfies S(r,f)=o(T(r,f))as r→∞,possibly outside a set of r of finite logarithmic measure.
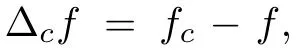
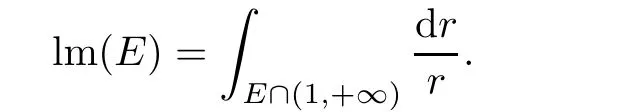
A set E∈(1,+∞)is said to have finite logarithmic measure if lm(E)<∞.
Differential equations were studied in many aspects(see,for example,[3,4,17]).Some expositions consider(system of)difference equations in real domains.So far,the previous researches are only on complex differential(difference)equations(systems)([5–8])or functional equations,but not on composite functional-differential equations(systems).Therefore,it is very important and meaningful to study the cases of composite functional-differential equations(systems).That will be an innovative contribution of this article.
The remainder of this article is organized as follows.In Section 2,we will investigate some properties of meromorphic solutions on three types of composite functional-differential equations,such as existence,growth order,and the estimate of the non-integrated function.In Section 3,we will investigate the behaviour of meromorphic solutions of a system of composite functional equations,and four theorems are obtained and some examples are constructed to show that the results hold.
2 Existence of Meromorphic Solutions of Composite Functional-Differential Equations and Form of Composite Functional-Differential Equations
In 2003,H.Silvennoinen([19])was devoted to considering many types of composite functional equations,and he got some good results,for example,the following Theorem 2.1 is one of his results.
Theorem 2.1([19]) The composite functional equation
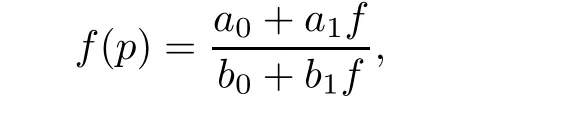
where the coefficients{ai},{bj}(i,j=0,1)are of growth S(r,f)such thatand p is a polynomial of degp=k≥2,does not have any meromorphic solutions.
A question is whether or not the assertion of Theorem 2.1 remains valid,if we replace the equation
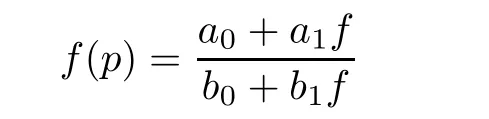
with the following form
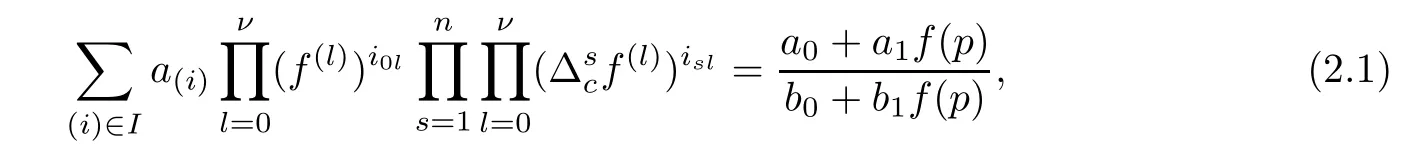
where the coefficients{ai},{bj},and{a(i)}are of growth S(r,f)such thatp is a polynomial of degp=k≥2.
In this section,the authors will pay attention to considering the properties of meromorphic solutions on types of composite functional-differential equations in complex domain,and extend the results obtained by H.Silvennoinen([19]),which is different from the complex differential equations or systems of complex differential equations.
At this point,we pause brie fly to introduce the notations used in this article.Let I be a finite set of multi-indexes i=(i0,···,in),J be a finite set of multi-indexes j=(j0,···,jn).Differential-difference polynomials ?1(z,f),?2(z,f)of a meromorphic function f(z)are defined as
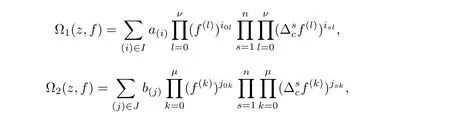
where each{a(i)},{b(j)}is a small meromorphic function with respect to f.
We denote that
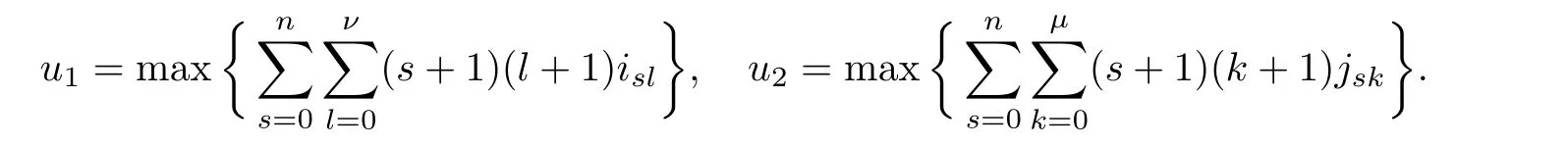
First,we will investigate the existence of meromorphic solutions of a type of composite functional-differential equations(2.1),and for this equations,the main theorem can be stated below.
Theorem 2.2Let u1 Example 2.1 shows that Theorem 2.2 does not hold if ai,bjand a(i)are not of growth S(r,f);there may exist a rational solution. Example 2.1Let p(z)=z2,c=1.Then,functionis a solution of equation Second,we will study the form of p(z)of composite functional-differential equations as follows: where p(z)is an entire function,{ai},{a(i)},{b(j)}are small functions of f. We obtain the following result. Theorem 2.3Let f be a non-constant meromorphic solution of the composite functional differential equations(2.2).Then,p is a polynomial. Third,we shall estimate the non-integrated counting function of meromorphic solutions of the following composite functional-differential equation where{ai}are meromorphic functions,and p is a polynomial of degree k≥2. We get the main results below. Theorem 2.4Let f be a finite order transcendental meromorphic solution of(2.3),{a(i)}be polynomials,then where K and s are positive constants,and r is large enough.If s where Example 2.2 shows that the condition s Example 2.2Let Then, In this case,f satisfies However,by k≥2,we have It shows that Theorem 2.4 does not hold if s=k. To prove Theorem 2.2-2.4,we need some lemmas as follows. Lemma 2.5([11]) Let f be a transcendental meromorphic function and p be a polynomial of degree k ≥ 1.GivenletThen,given ε >0,for anyand for r large enough,we have Lemma 2.6([6]) Let ψ:[r0,+∞)→ (0,+∞)be positive and bounded in every finite interval.Suppose that whereμ>0,m>1,A>1,and B are real constants.Then, Lemma 2.8([1]) Let f be a non-constant meromorphic function and g be a transcendental entire function.Then,there exists an increasing sequence,rn→∞,such that holds for r=rn. Lemma 2.9([16])Let g:(0,+∞)→ R,h:(0,+∞)→ R be monotone increasing functions such that g(r)≤h(r)outside of an exceptional set E of finite linear measure.Then,for any α >1,there exists r0such that g(r) ≤ h(αr)for all r>r0. Lemma 2.10([15]) Let T:[0,+∞)→[0,+∞)be a non-decreasing continuous function,δ∈(0,1),and s∈(0,∞).If T is of finite order,then where r runs to infinity outside of a set of finite logarithmic measure. Lemma 2.11Let f be a meromorphic function of finite order,and ?1(z,f)and ?2(z,f)be defined as above.Then, and ProofFirst,we estimate m(r,?1(z,f)). In order to estimate the poles of ?1(z,f),we consider the term of According to Lemma 2.10,we obtain We can obtain the followings: Hence,it yields that Immediately,we get where r runs to infinity outside of a set of finite logarithmic measure. Similar to the proof of ?1(z,f),we obtain Hence,we deduce that Lemma 2.13([19]) Let f be a meromorphic function.Then,T(r,f)is an increasing convex function of logr andis an increasing function of r. Proof of Theorem 2.2First,we suppose that f is a transcendental meromorphic solution of composite functional-differential equation(2.1). For a sufficiently small ε>0,by Lemma 2.5,Lemma 2.7,and Lemma 2.11,one observes that Hence,by Lemma 2.9,for α>1 and r large enough,it gives Set t=αr.Then, Using Lemma 2.6 to the above inequality,it yields thatwith α1=so there is a contradiction. Second,suppose that f is a rational solution of(2.1).Then,the coefficientsa1(z),b0(z),b1(z)must be constants. Set From the above equation,we haveandcan not hold at the same time.Otherwise,where c is a constant. Hence,we get From the above equation,it gives u1≥k,a contradiction with the assumption u1 Combining the first step with the second step above,the assertion follows. Proof of Theorem 2.3To the contrary,we assume that p is a transcendental entire function.Then,we have For any given K>30 and for r large enough,we have M(r,p)>rK.According to Lemma 2.8,for any n there exists an increasing sequence rn→∞such that Applying Lemma 2.11 and Lemma 2.12 to(2.2),we get outside a possible exceptional set of finite linear measure. Furthermore,using Lemma 2.9 to the above inequality,for?α >1,r≥ rα,it concludes In addition,from Lemma 2.8,we have By(2.4),(2.5)and(2.6),as n→∞,one concludes that As K can be arbitrarily large,(2.7)is a contradiction.Thus,p is a polynomial. Proof of Theorem 2.4Suppose that f is a transcendental meromorphic solution of(2.3)with finite order.According to Lemma 2.11,we have By Lemma 2.5,we have Combining(2.8)and(2.9),it gives Furthermore,we have where s0=max{s,1}. As n(r,f)is a increasing function of r and k>s0,then by(2.10)and Lemma 2.6,one observes that where Thus,we have completed the proof of Theorem 2.4. Gao et al had also discussed the existence or growth of some types of systems of complex difference equations,and obtained some results([5–8]).Now,we will consider meromorphic solution of the following system of composite functional equation The growth order of meromorphic solutions(f1,f2)of(3.1)is defined by As regards(3.1),we obtain the following four Theorems. Theorem 3.1Let Q1(z),Q2(z)be of the reduced formwhere P1,P2are polynomials with d1=degP1(z),d2=degP2(z),and l is a non-zero integer.Then,all meromorphic solutions(f1(z),f2(z))of(3.1)are of the reduced formwhere g1,g2are polynomials and p≥l. Example 3.1is a meromorphic solution of the system of composite functional equation of the form Theorem 3.2Let Q1(z),Q2(z)be meromorphic such that Q1(z),Q2(z)have exactly one nonzero pole,then all component fi(z)of meromorphic solutions(f1(z),f2(z))of(3.1)have infinitely many poles. Theorem 3.3Letbe constants satisfying the conditionare polynomials,Then,(3.1)possesses exactly one meromorphic solution(f1,f2),which is an entire function of growth order Example 3.2We can see that is an entire solution of the system of the composite functional equation so and making use of the Stirling formula we can conclude that ρ(f1)= ρ(f2)=1.This example shows that Theorem 3.3 holds. Theorem 3.4Letbe constants satisfying the conditionand let Q1(z),Q2(z)be of the reduced formwhereare entire functions,l is a non-zero integer.Then,(3.1)possesses exactly one meromorphic solution(f1(z),f2(z)),which has the reduced formwhere g3,g4are entire functions. To prove Theorems 3.1–3.4,we need the following Lemma. Proof of Theorem 3.1We first prove that z0=0 is a pole of f1,f2. Hence, Substituting(3.2)into the second equation of(3.1),we obtain where It follows from f1(z0)=∞that at least one of the valuesmust be infinite,it is to say,there exists at least one index i0∈{1,2,...,2n}such thatThen by we can see that at least one of the valuesmust be infinite. Let i1∈{1,2,...,2n}such that.By repeating this process,we see that there is a sequence of poles of f1accumulating to the origin,which is a contradiction.Hence,f1(z)may only have a pole at the origin. By a similar reasoning as above,it is easily obtained that f2(z)may only have also a pole at the origin. Suppose now that f1(z)has a pole of order p at the origin.It follows immediately from(3.3)that p≥l.Then,g1(z)=f1(z)zpis entire and satisfies Let d=max{d1,d2}.We differentiate(3.4)d+p?l+1 times with respect to z to obtain Then, where B is a constant. For any r≥R,there exists a positive integer m such that Combining(3.6)with(3.7),we obtain Hence, Analogously to(3.2)–(3.9),we have,which is a rational function having no non-zero poles,where g2is a polynomial. Now,we prove p=q. On one hand,from the second equation of(3.1),we have then it immediately deduces that q≥p. On the other hand,from(3.2),we can get q≤p.Thus,we proved that p=q. Hence,all meromorphic solutions(f1(z),f2(z))of(3.1)are of the reduced formwhere g1,g2are polynomials and p≥l. Proof of Theorem 3.2Let Q2(z)be a meromorphic function having exactly one nonzero pole at z0.Then,we obtain,from(3.3), As Q2(z0)=∞,then it is clear that at least one of the values f1(ciz0)must be infinite. Let i0∈max{0,1,2,...,2n}such that.Suppose that i0≥1. We instead z by ci0z0in(3.10)to obtain Similar to the proof of Theorem 3.1,we see that there is a sequence of poles of f1accumulating to the origin,which is a contradiction. It shows that i0=0 and z0is a pole of f1. By continuing in this fashion,we get an increasing sequence{mi}of integers,such that the sequenceis a pole sequence of f1outside the origin.Similar to the proof of f1,we get an increasing sequence{mj}of integers,such that the sequenceis a pole sequence of f2outside the origin. Thus,we complete the proof of Theorem 3.2. Proof of Theorem 3.3By the conditionand Lemma 3.5,we can see that(3.1)possesses exactly one meromorphic solution(f1,f2),which is entire. Similar to(3.3),we get Hence, where C1,C2,A>0 are finite constants.Then,there exists B>0 and R>0 such that For any r≥R,take an integer m such that(3.8)holds.Then Hence,we complete the proof of Theorem 3.3. Proof of Theorem 3.4From(3.1),we obtain where Mi(i=0,···,2n)are given in Theorem 3.1. has no nontrivial solutions.Hence,(3.14)possesses exactly one meromorphic solution f1(z). We can obtain a formal solution of(3.14)by a series expansion at the origin. Set From(3.14),we have Substitute f1and Q1,Q2into(3.15)to obtain that is, Comparing the coefficients of zmand making use of the assumption M0+M1c+...+we get q1=l and Thus,zlf1(z)is an entire function. From(3.1),we obtain By a similar reasoning as above,zlf2(z)is an entire function. Hence,Theorem 3.4 is proved.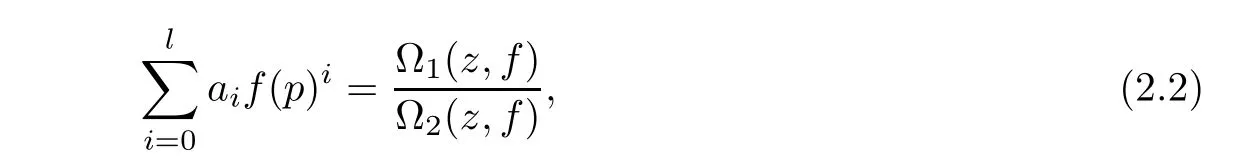

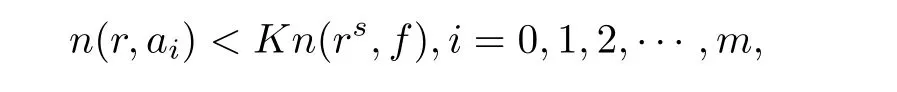
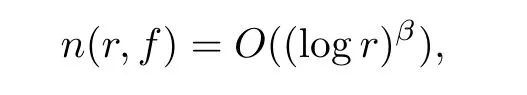
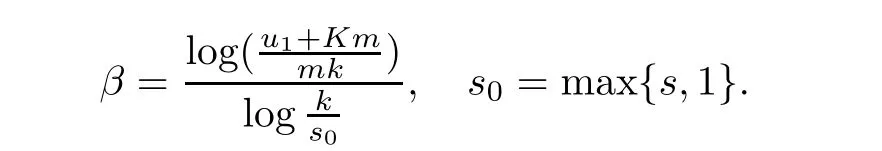
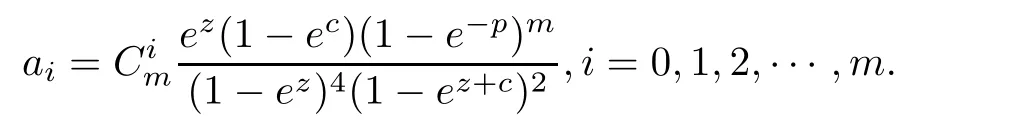
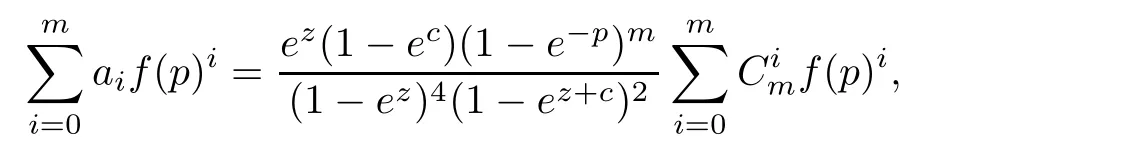
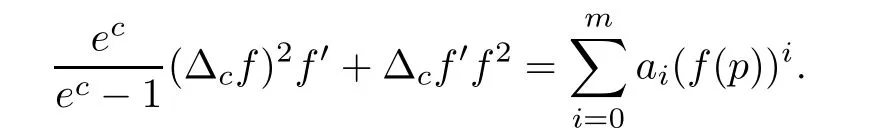
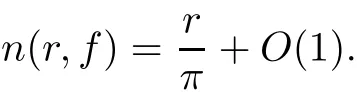
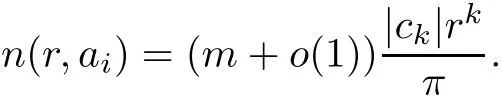
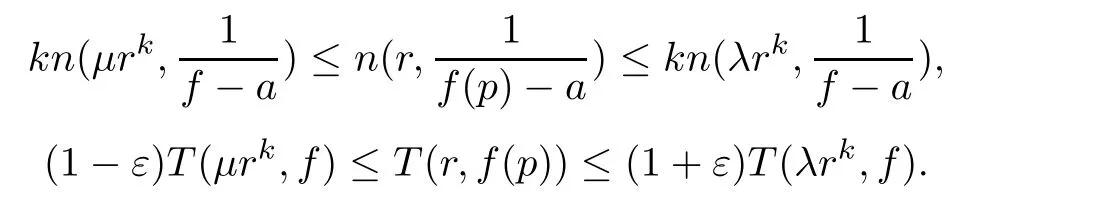
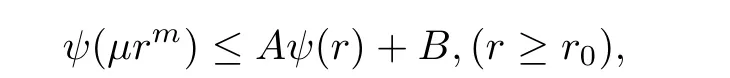
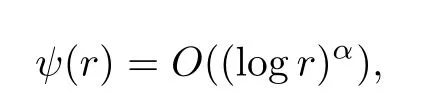
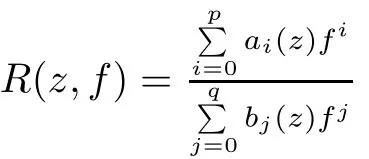

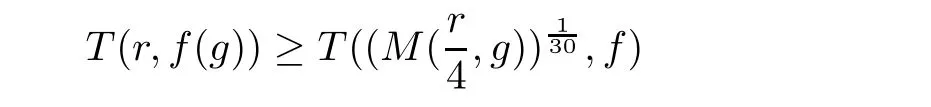

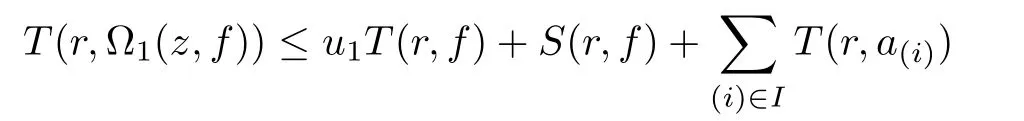
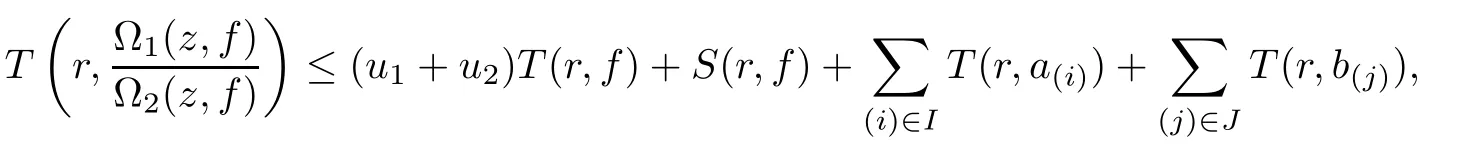
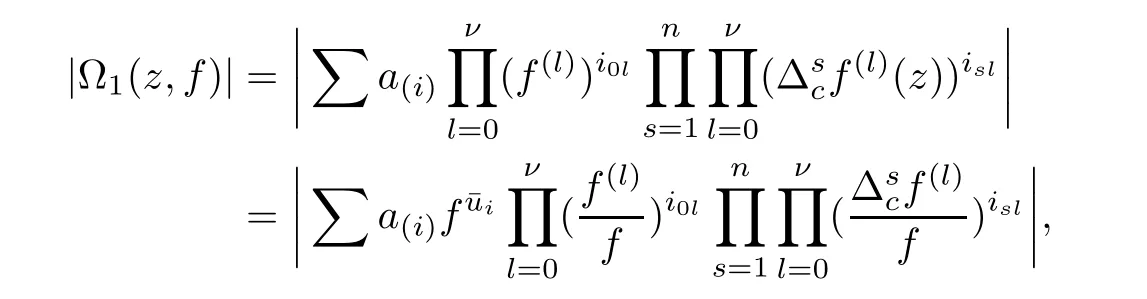
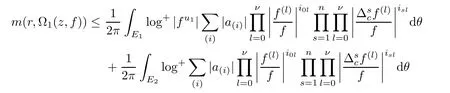
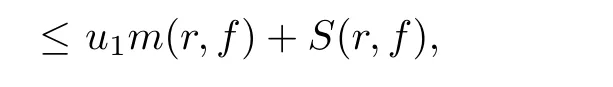
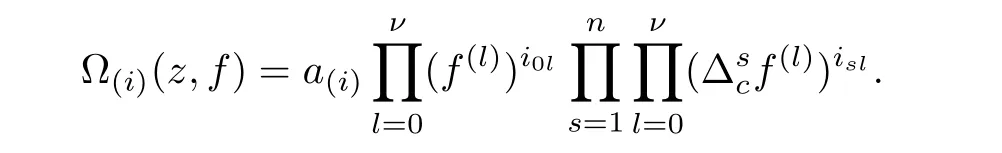
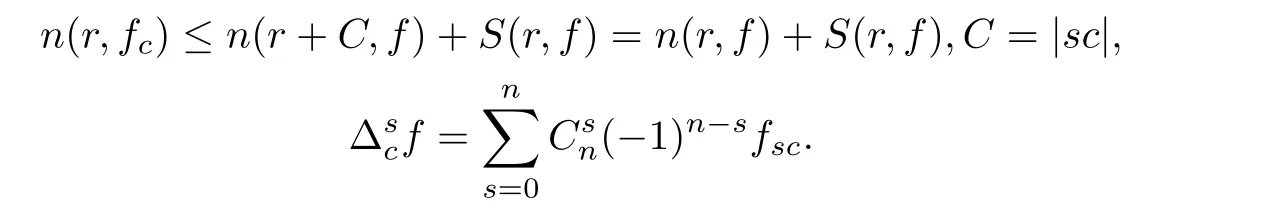
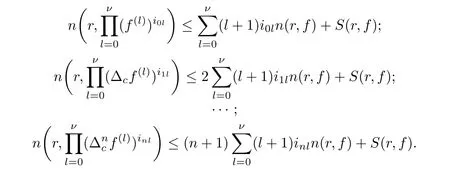
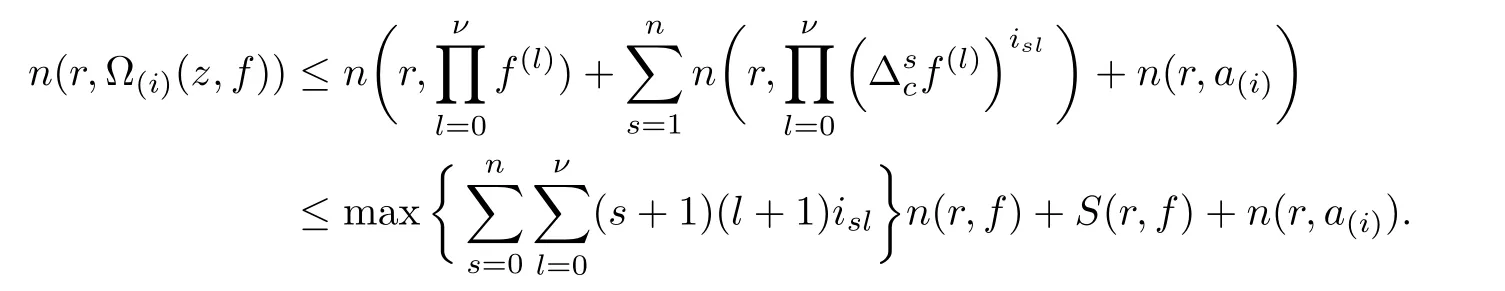
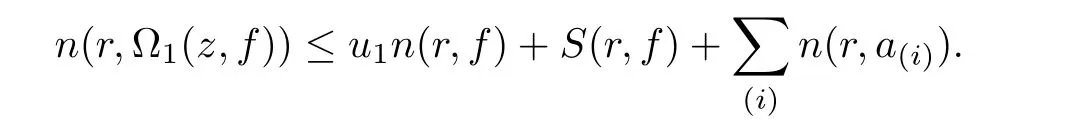
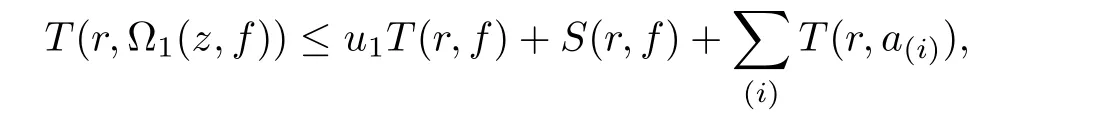
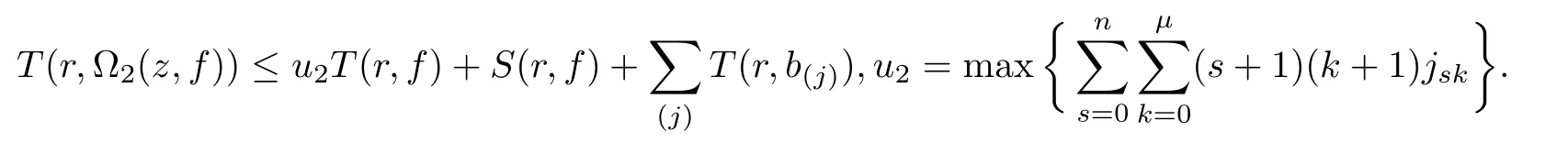

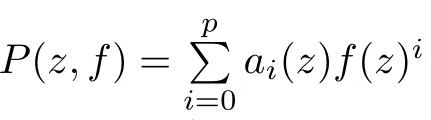
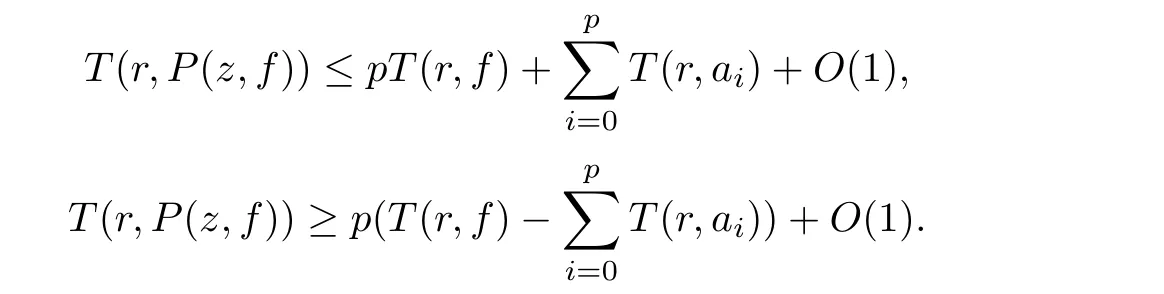
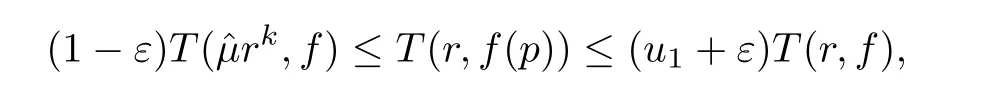
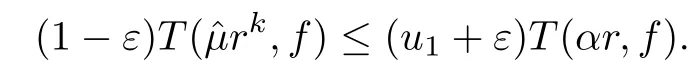
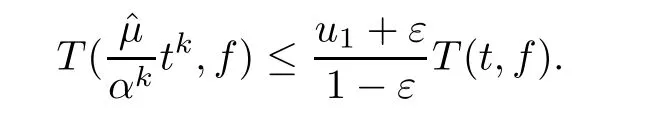
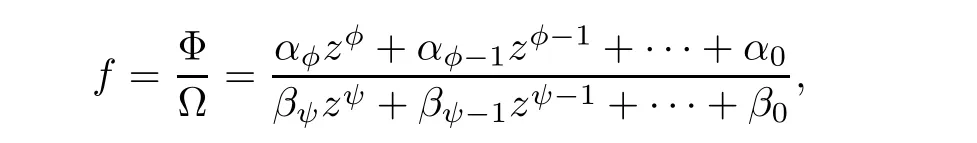
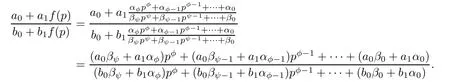

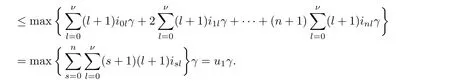
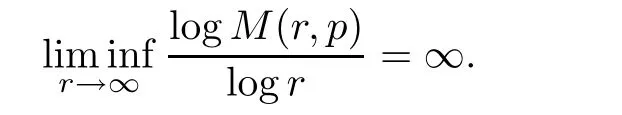
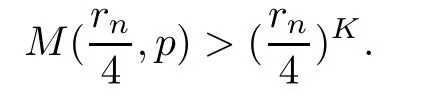
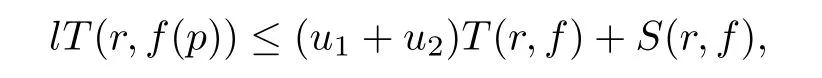
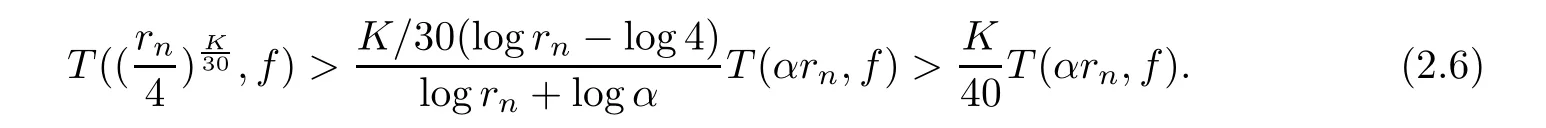
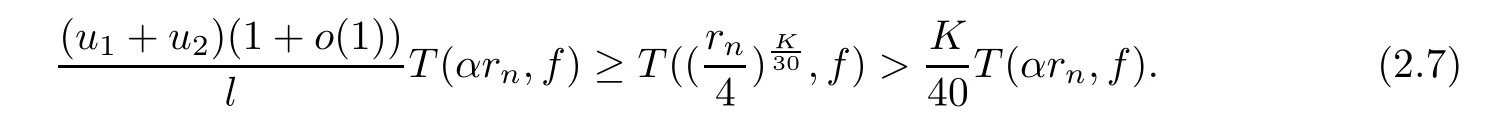

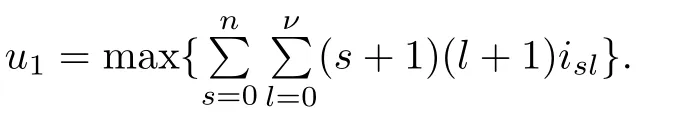

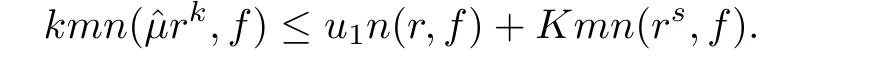
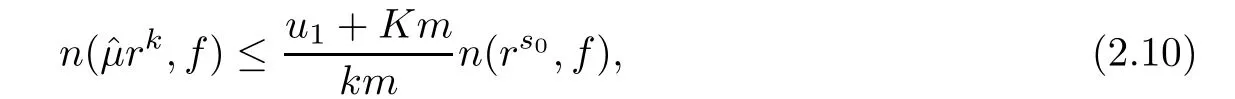
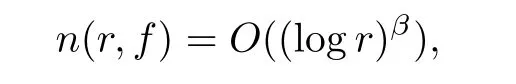
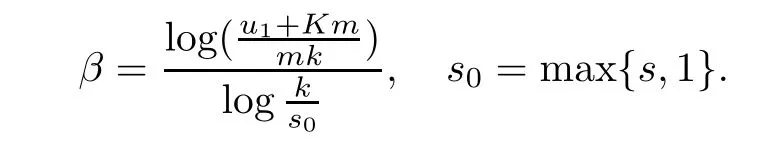
3 Some Results on System of Complex Composite Functional Equations
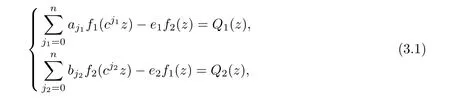
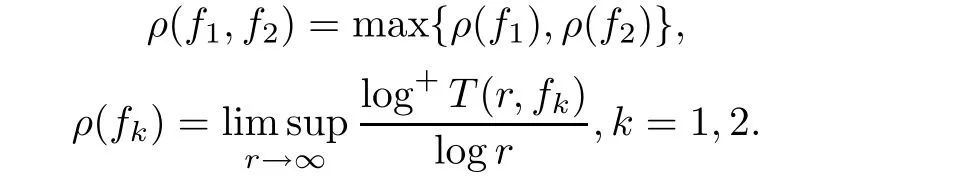
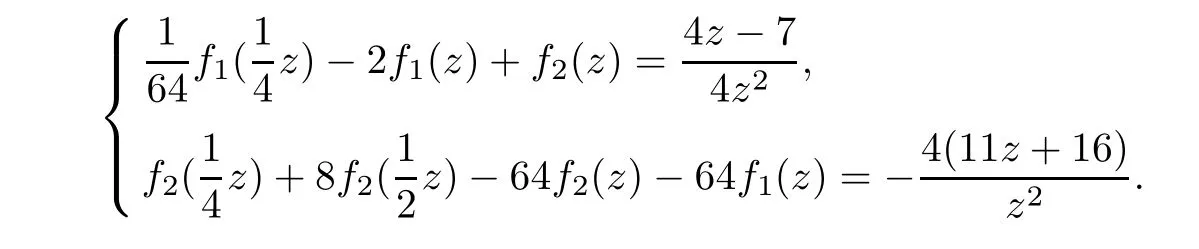
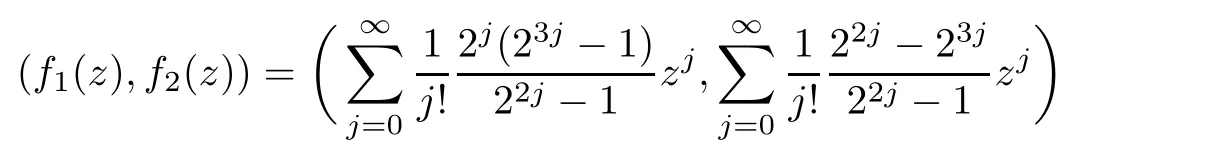
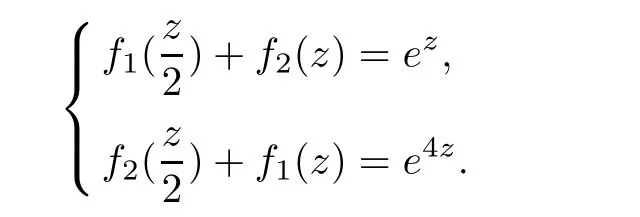
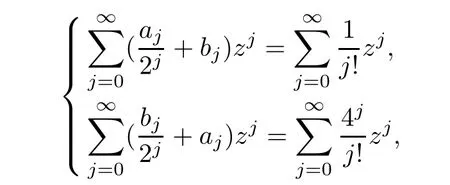
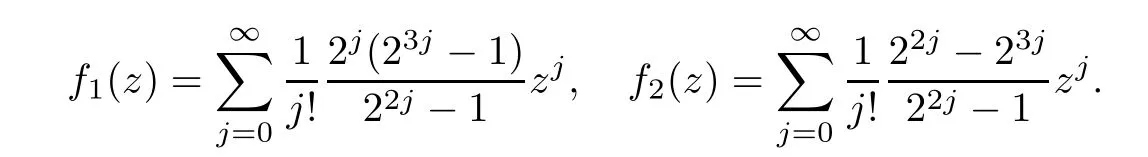
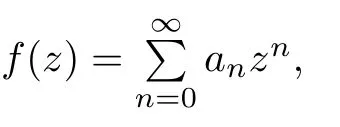
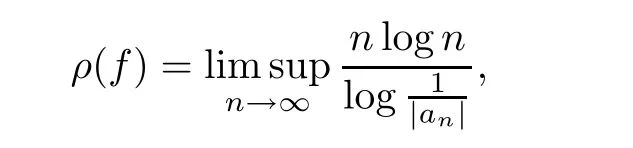
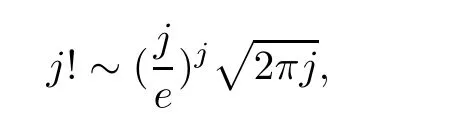
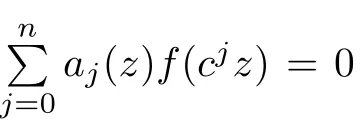
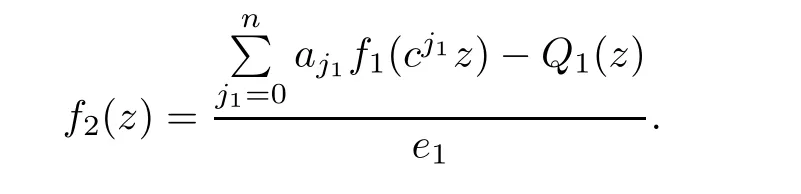
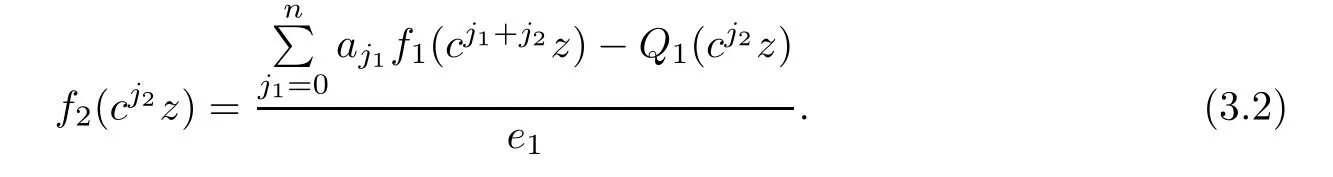
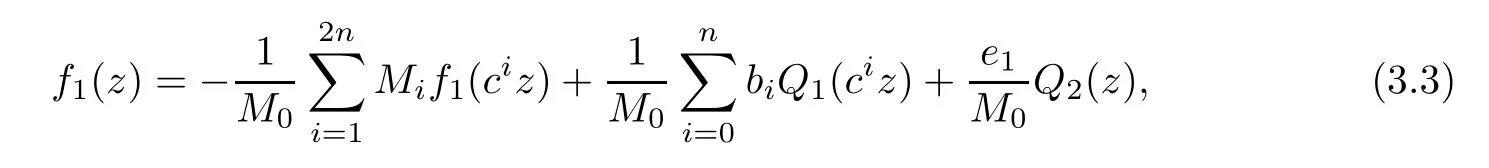
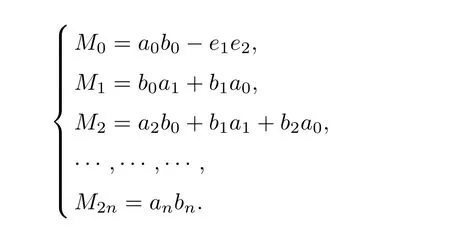
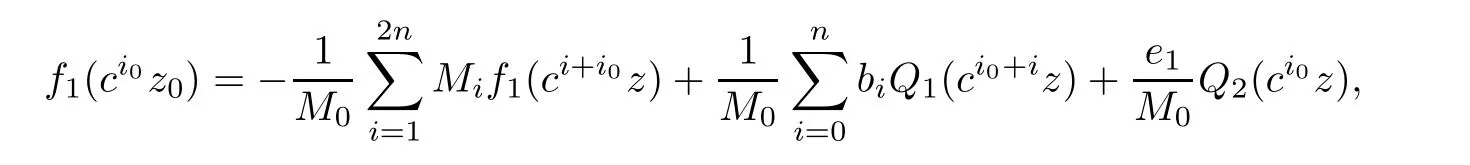
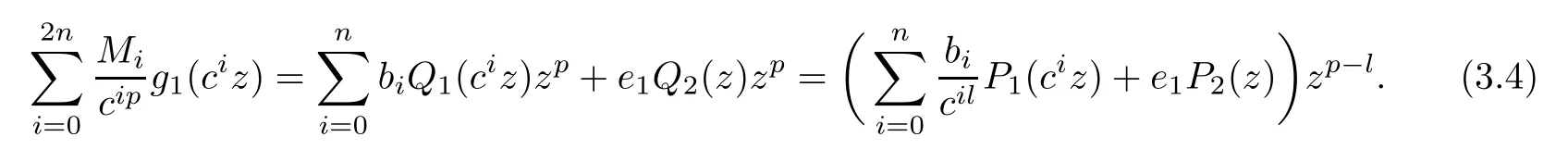
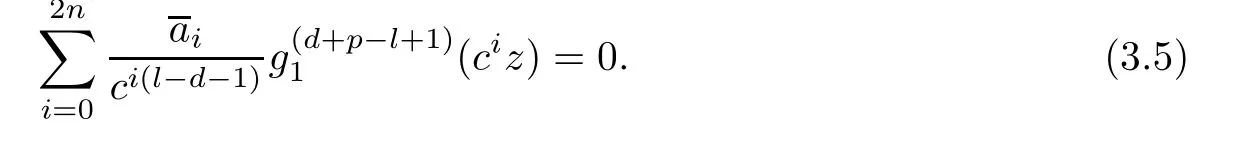
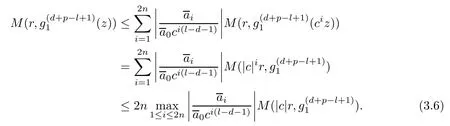
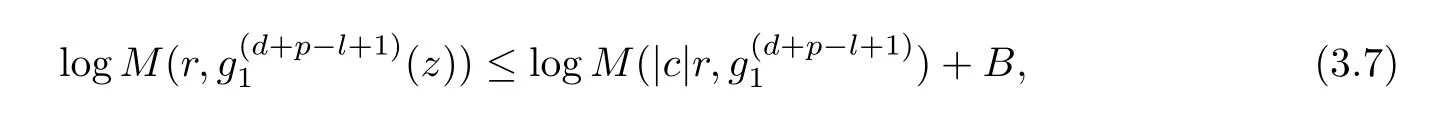

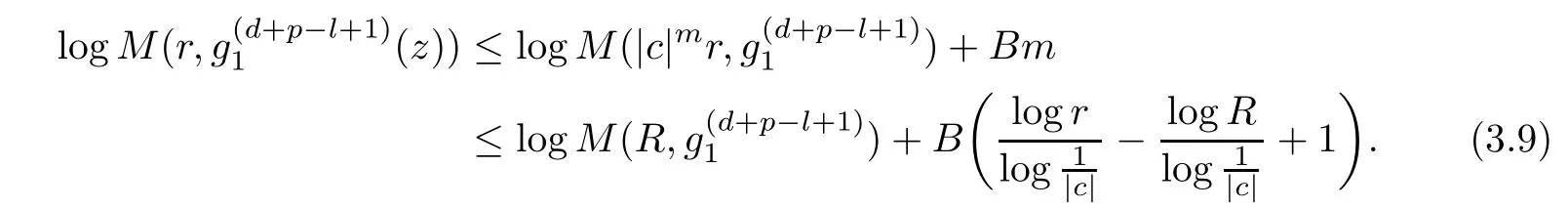
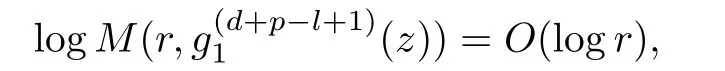
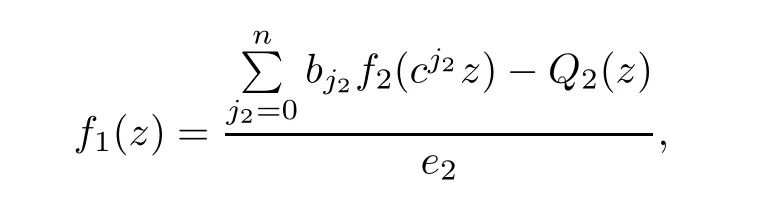
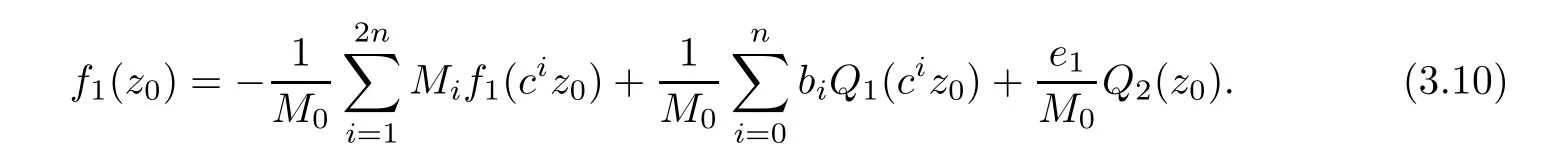
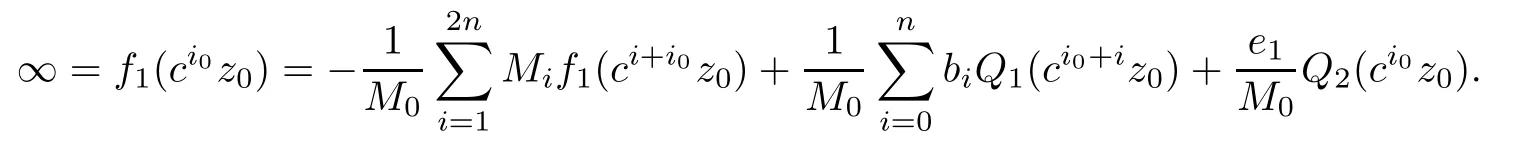
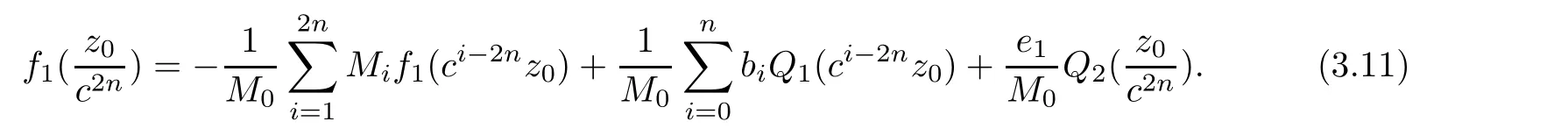
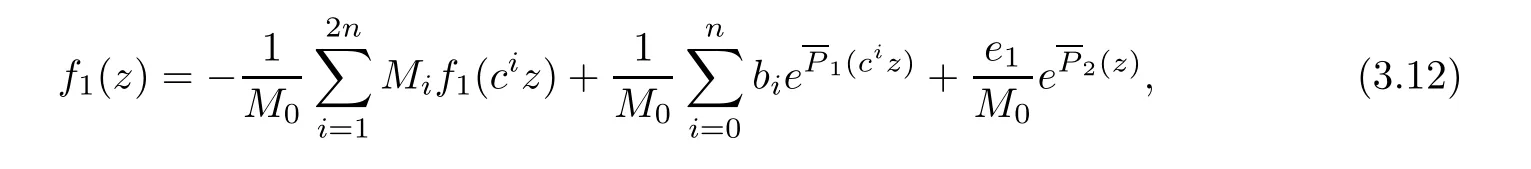
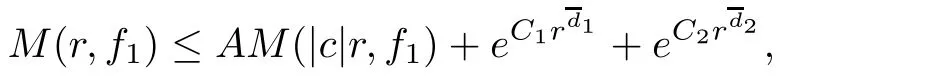
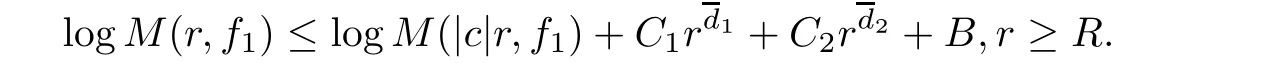
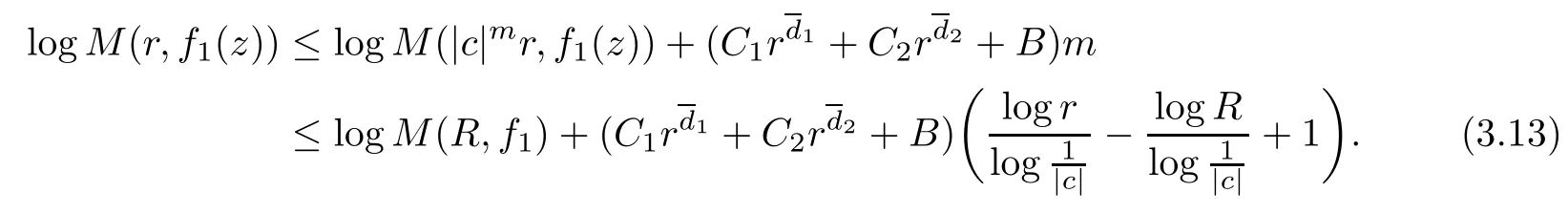
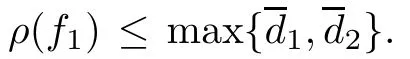
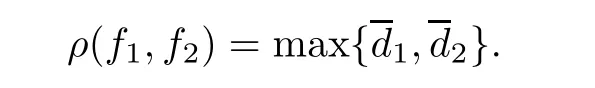
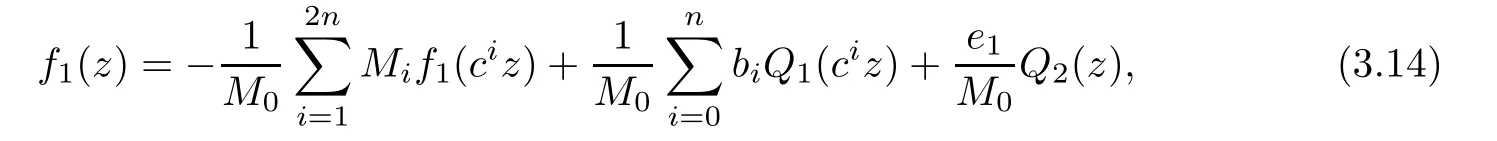
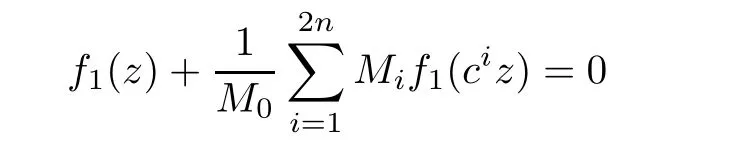
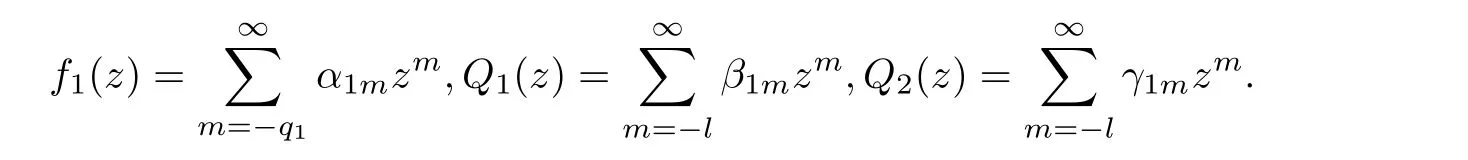
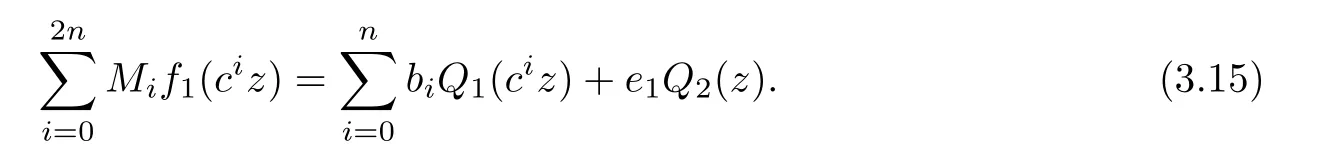
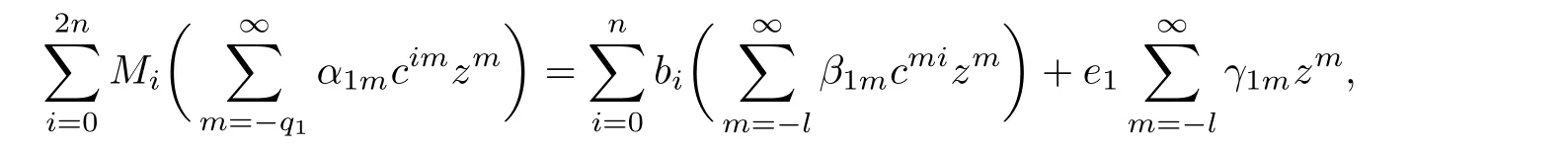
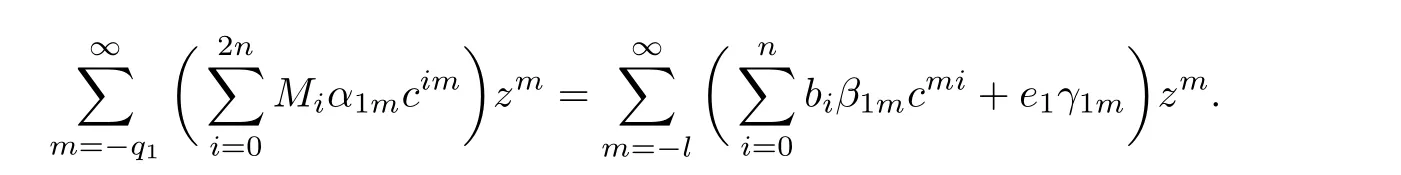
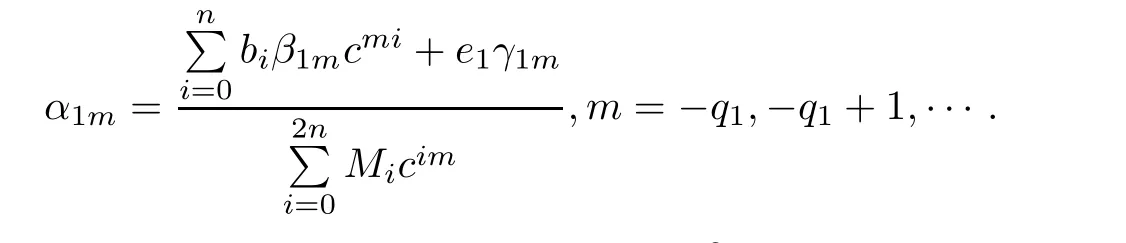
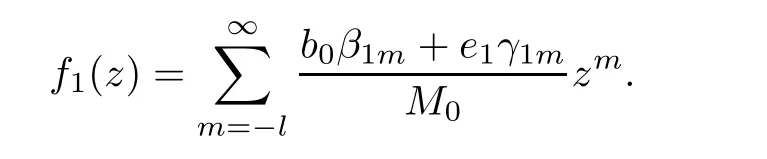
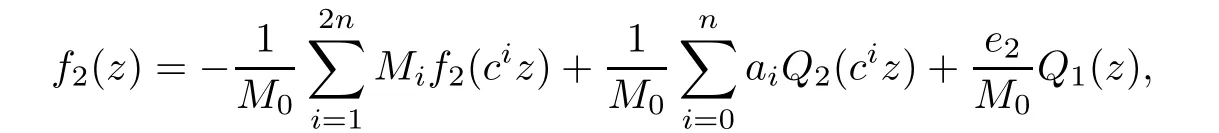
 Acta Mathematica Scientia(English Series)2020年2期
Acta Mathematica Scientia(English Series)2020年2期
