STRONG INSTABILITY OF STANDING WAVES FOR A SYSTEM NLS WITH QUADRATIC INTERACTION?

Laboratoire Paul Painlevé UMR 8524,Université deLille CNRS,59655 Villeneuve d’Ascq,Cedex,France

Department of Mathematics,HCMC University of Pedagogy,280 An Duong Vuong,Ho Chi Minh,Vietnam

E-mail:contact@duongdinh.com

Abstract We study the strong instability of standing waves for a system of nonlinear Schr?dinger equations with quadratic interaction under the mass resonance condition in dimension d=5.

Key words System NLS quadratic interaction;ground states;instability;blow-up

1 Introduction

We consider the system NLS equations

The system(1.1)is regarded as a non-relativistic limit of the system of nonlinear Klein-Gordon equations

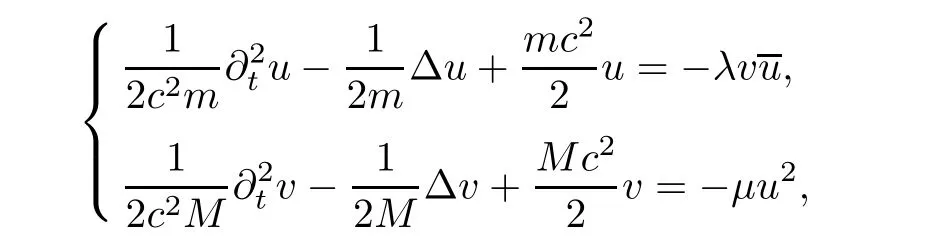
under the mass resonance condition

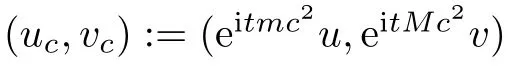
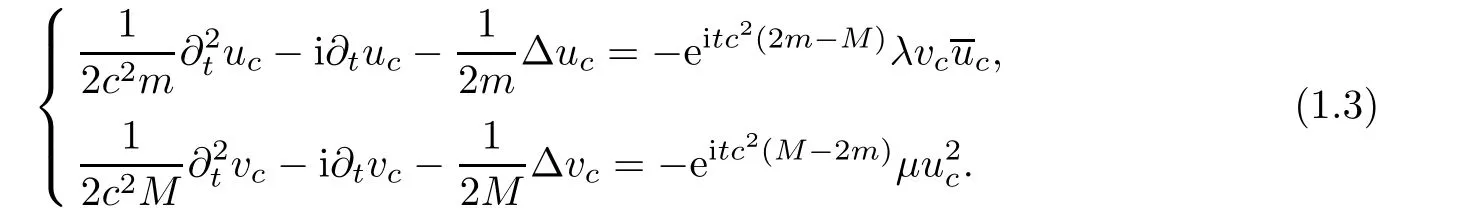
We see that the phase oscillations on the right hand sides vanish if and only if(1.2)holds,and system(1.3)formally yields(1.1)as the speed of light c tends to infinity.System(1.1)also appears in the interaction process for waves propagation in quadratic media(see e.g.[3]).

System(1.1)has attracted a lot of interest in past several years.The scattering theory and the asymptotic behavior of solutions were studied in[10–12,14].The Cauchy problem for(1.1)in L2,H1and in the weighted L2space hxi?1L2=F(H1)under mass resonance condition were studied in[13].The space-time analytic smoothing effect was studied in[7–9].The sharp threshold for scattering and blow-up for(1.1)under the mass resonance condition in dimension d=5 was studied in[6].The existence,stability of standing waves and the characterization of finite time blow-up solutions with minimal mass were studied recently in[4].

Let us recall the local well-posedness in H1for(1.1)due to[13].To ensure the conservation law of total charge,it is natural to consider the following condition:

Proposition 1.1(LWP in H1[13]) Let d≤ 6 and let λ and μ satisfy(1.4).Then,for any(u0,v0)∈H1×H1,there exists a unique paire of local solutions(u,v)∈Y(I)×Y(I)of(1.1)with initial data(u(0),v(0))=(u0,v0),where

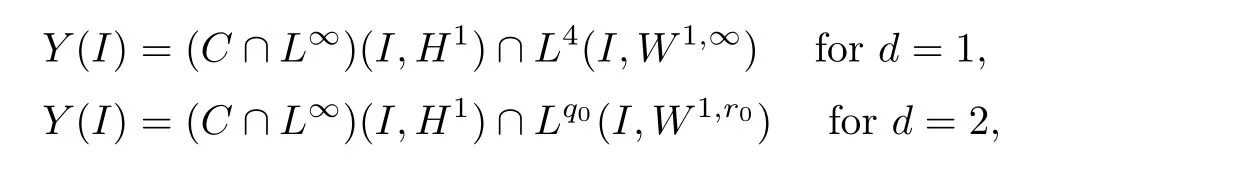
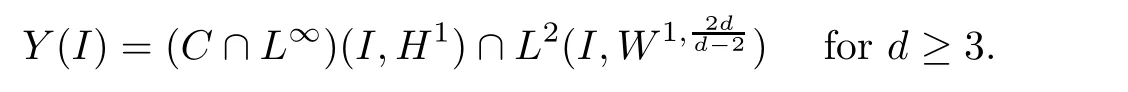
Moreover,the solution satisfies the conservation of mass and energy:for all t∈I,

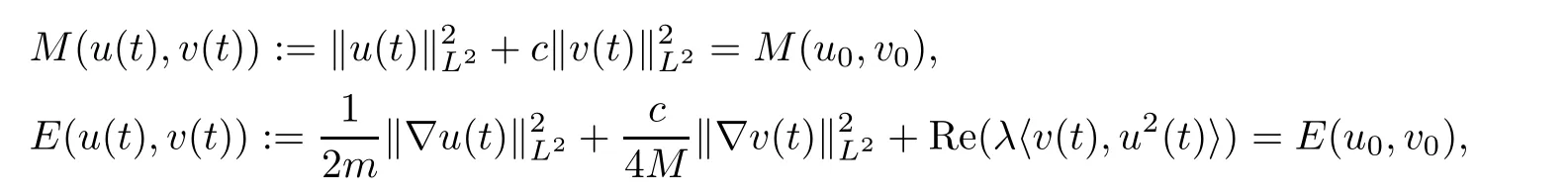
We now assume that λ and μ satisfy(1.4)with c>0 andBy change of variables

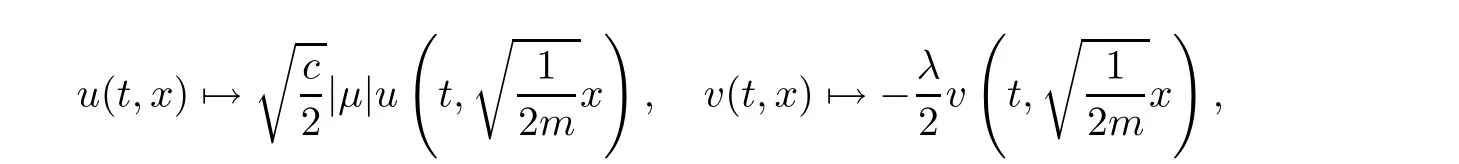
system(1.1)becomes

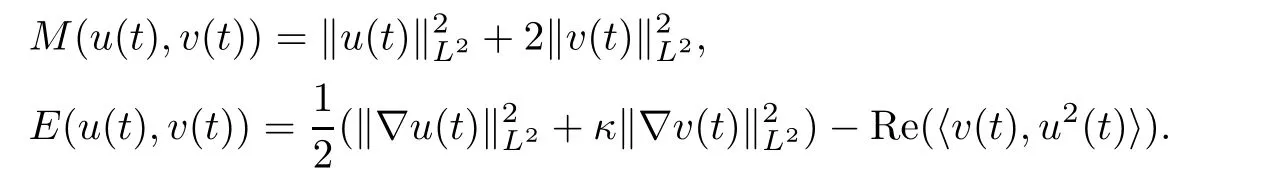
The local well-posedness in H1for(1.5)reads as follows.

Proposition 1.2(LWP in H1) Let d≤6.Then for any(u0,v0)∈H1×H1,there exists a unique pair of local solutions(u,v)∈Y(I)×Y(I)of(1.5)with initial data(u(0),v(0))=(u0,v0).Moreover,the solution satisfies the conservation of mass and energy:for all t∈I,

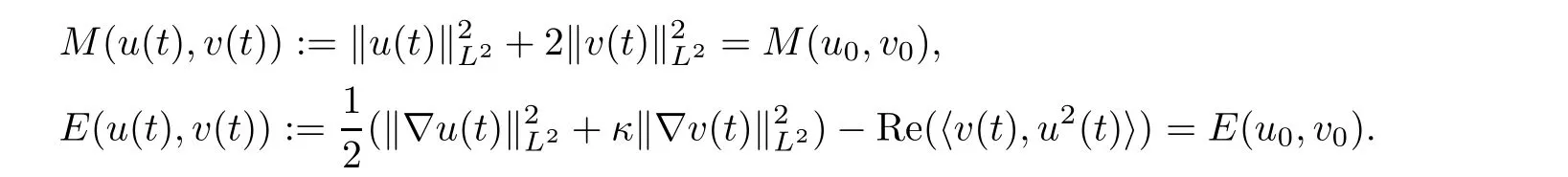
The main purpose of this article is to study the strong instability of standing waves for system(1.5)under the mass resonance conditionin dimension d=5.Let d=5 and consider

Throughout the sequel,a standing wave is a solution to(1.6)of the formwhere ω ∈ R is a frequency and(φω,ψω) ∈ H1× H1is a non-trivial solution to the elliptic system

We are interested in showing the strong instability of ground state standing waves for(1.6).Let us first introduce the notion of ground states related to(1.6).Denote

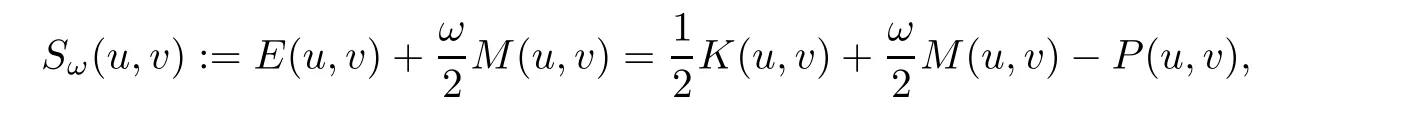
where

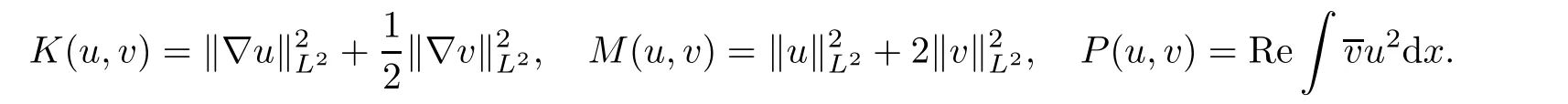
We also denote the set of non-trivial solutions of(1.7)by

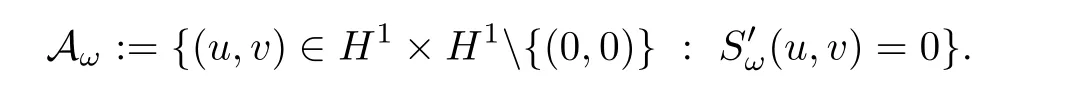
Definition 1.3A pair of functions(φ,ψ)∈ H1×H1is called ground state for(1.7)if it is a minimizer of Sωover the set Aω.The set of ground states is denoted by Gω.In particular,

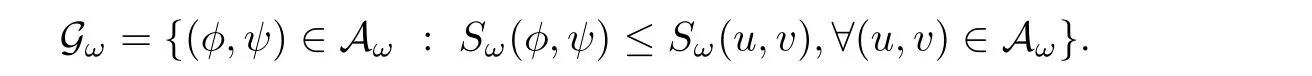
We have the following result on the existence of ground states for(1.7).

Proposition 1.4Let d=5,and ω >0.Then,the set Gωis not empty,and it is characterized by

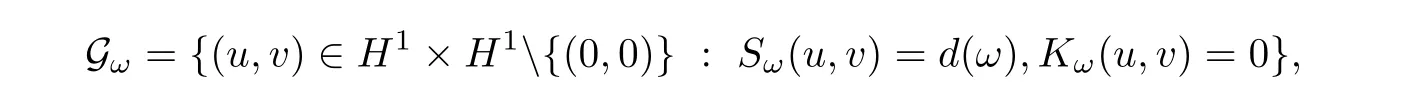
where

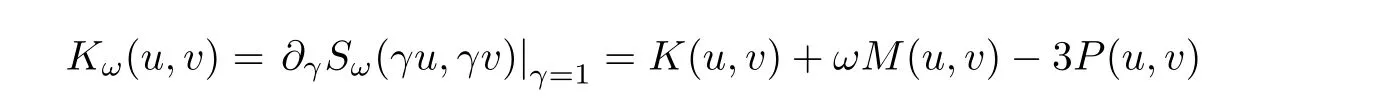
is the Nehari functional and

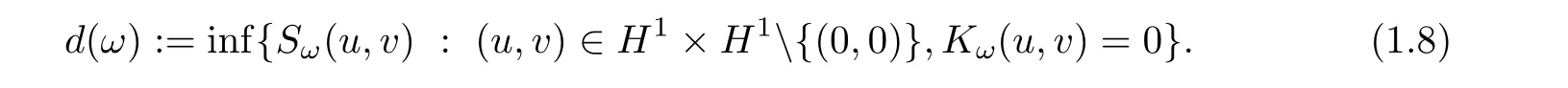
The existence of real-valued ground states for(1.7)was proved in[13](actually for d≤5 and κ>0).Here,we proved the existence of ground states(not necessary real-valued)and proved its characterization.This characterization plays an important role in the study of strong instability of ground states standing waves for(1.6).We only state and prove Proposition 1.4 for d=5 andHowever,it is still available for d ≤ 5 and κ >0.

We also recall the definition of the strong instability of standing waves.

Definition 1.5We say that the standing waveis strongly unstable if for any ?>0,there exists(u0,v0)∈ H1× H1such thatand the corresponding solution(u(t),v(t))to(1.6)with initial data(u(0),v(0))=(u0,v0)blows up infinite time.

Our main result of this article is the following.

Theorem 1.6Let d=5,ω >0,and(φω,ψω) ∈ Gω.Then,the ground state standing wavesfor(1.6)is strongly unstable.

To our knowledge,this article is the first one that addresses the strong instability of standing waves for a system of nonlinear Schr?dinger equations with quadratic interaction.In[2],Colin-Colin-Ohta proved the instability of standing waves for a system of nonlinear Schr?dinger equations with three waves interaction.However,they only studied the orbital instability not strong instability by blow-up,and they only consider a special standing wave solution(0,0,e2iωt?),where ? is the unique positive radial solution to the elliptic equation

This article is organized as follows.In Section 2,we show the existence of ground states and its characterization given in Proposition 1.4.In Section 3,we give the proof of the strong instability of standing waves given in Theorem 1.6.

2 Exitence of Ground States

We first show the existence of ground states given in Proposition 1.4.To do so,we need the following pro file decomposition.

Proposition 2.1(Pro file decomposition) Let d=5 andLetbe a bounded sequence in H1×H1.Then,there exist a subsequence,still denoted bya familyof sequences in R5and a sequenceof H1×H1-functions such that

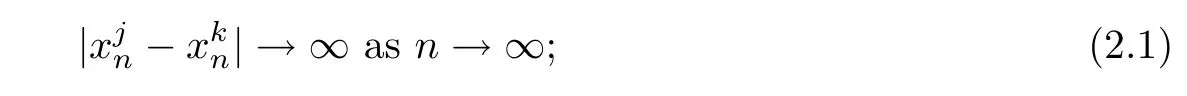
(2)for every l≥1 and every x∈R5,

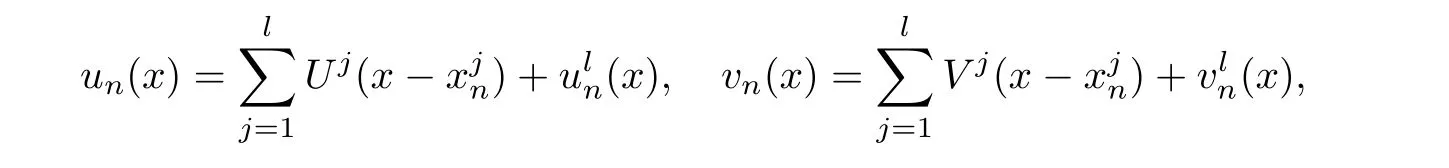
with

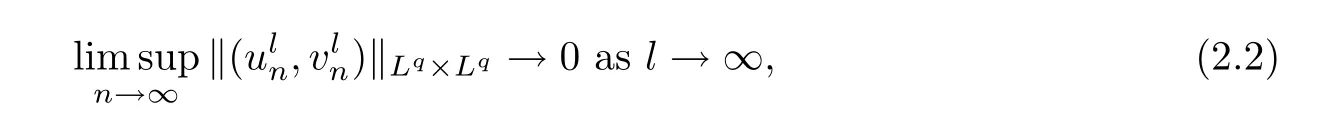
for every q∈(2,10/3).

Moreover,for every l≥1,

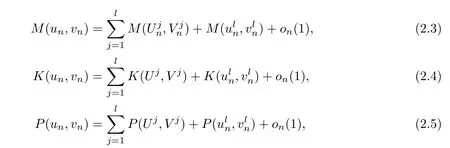
where on(1)→0 as n→∞.

We refer the reader to[4,Proposition 3.5]for the proof of this pro file decomposition.

The proof of Proposition 1.4 is done by several lemmas.To simplify the notation,we denote,for ω>0,

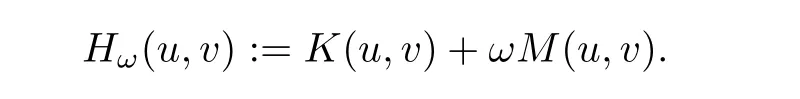
It is easy to see that for ω>0 fixed,we have

Note also that

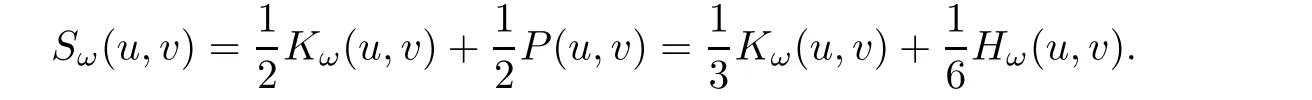
Lemma 2.2d(ω)>0.

ProofLet(u,v)∈ H1×H1{(0,0)}be such that Kω(u,v)=0 or H(u,v)=3P(u,v).From Sobolev embedding,we have

This implies that there exists C>0 such that

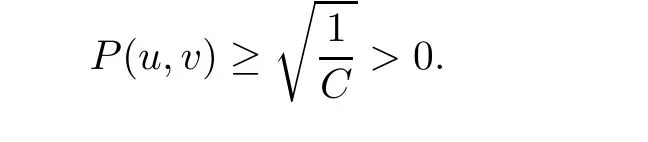
Thus,

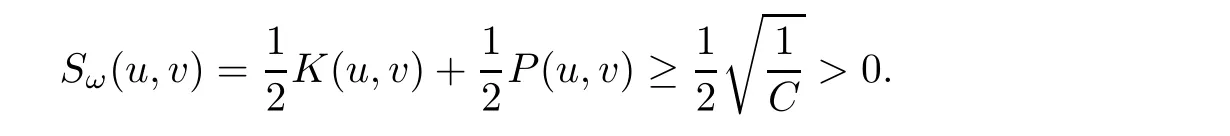
Taking the infimum over all(u,v)∈H1×H1{(0,0)}satisfying Kω(u,v)=0,we get the result.

We now denote the set of all minimizers for d(ω)by

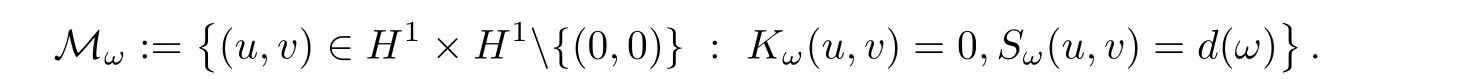
Lemma 2.3The set Mωis not empty.

ProofLet(un,vn)n≥1be a minimizing sequence for d(ω),that is,(un,vn) ∈ H1×H1{(0,0)},Kω(un,vn)=0 for any n≥1 andAs Kω(un,vn)=0,we have Hω(un,vn)=3P(un,vn)for any n≥1.We also have

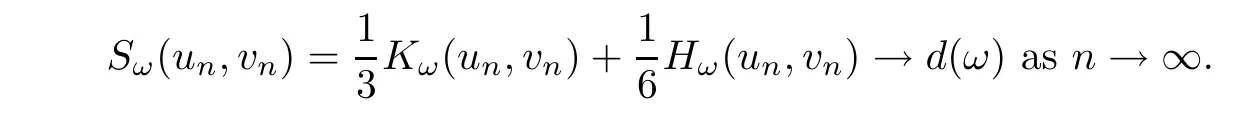
This yields that there exists C>0 such that

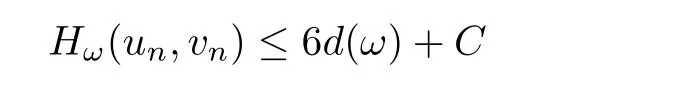
for all n ≥ 1.By(2.6),(un,vn)n≥1is a bounded sequence in H1×H1.We apply the pro file decomposition given in Proposition 2.1 to get(up to a subsequence)

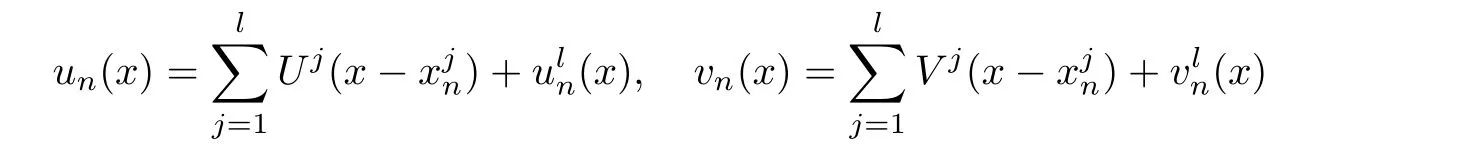
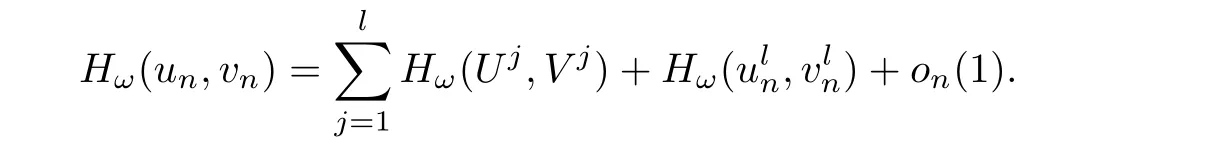
This implies that

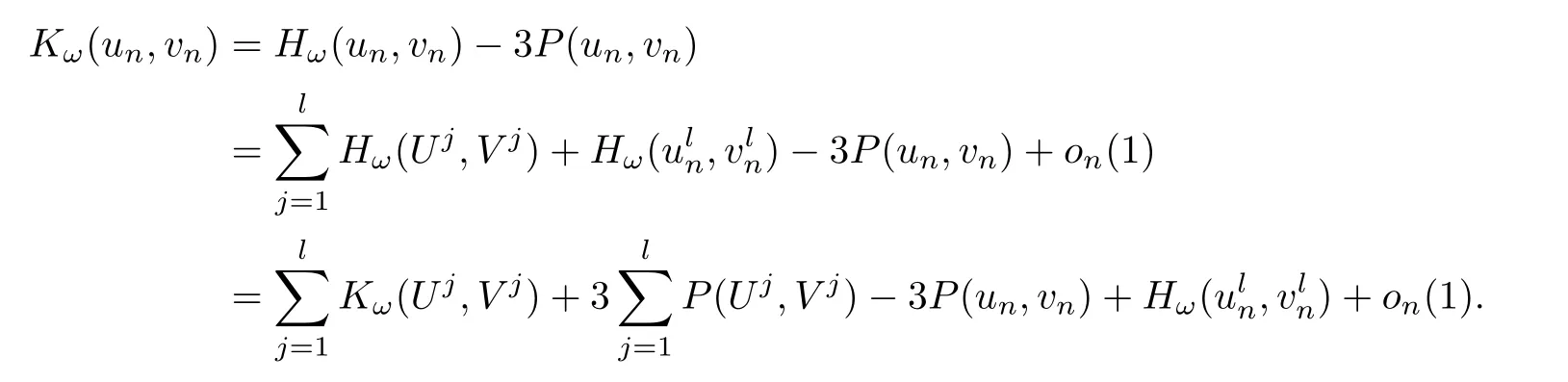
Because Kω(un,vn)=0 for any n≥ 1,P(un,vn)→2d(ω)as n→∞,andfor any n≥1,we infer that

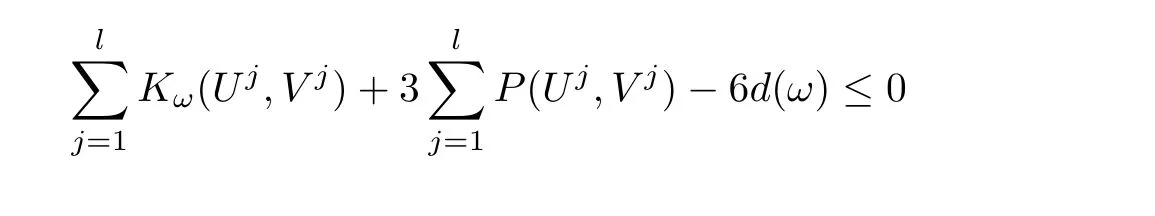
or

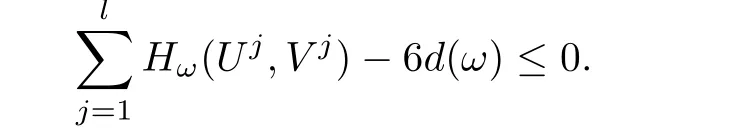
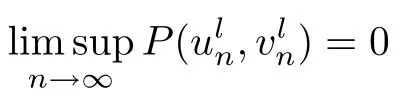
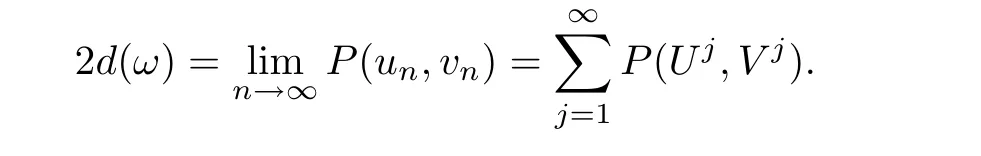
We thus obtain

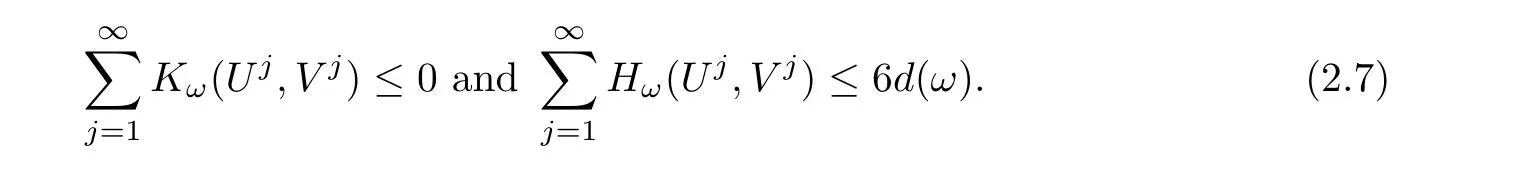
We now claim that Kω(Uj,Vj)=0 for all j≥ 1.Indeed,suppose that if there exists j0≥ 1 such thatthen we see that the equationadmits a unique non-zero solution

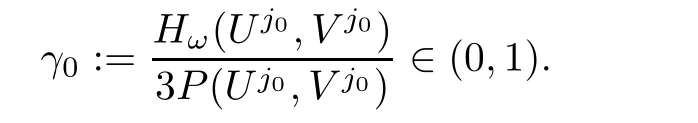
By the definition of d(ω),we have

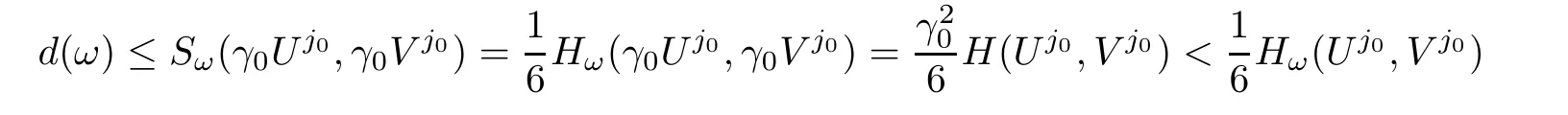
which contradicts to the second inequality in(2.7).We next claim that there exists only one j such that(Uj,Vj)is non-zero.Indeed,if there areandnon-zero,then by(2.7),bothare strictly smaller than 6d(ω).Moreover,as

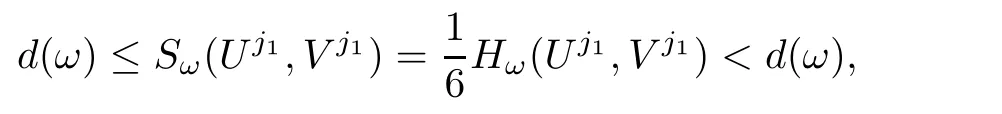
which is absurd.Therefore,without loss of generality,we may assume that the only one non-zero pro file is(U1,V1).We will show that(U1,V1)∈ Mω.Indeed,we have P(U1,V1)=2d(ω)>0,which impliesWe also have

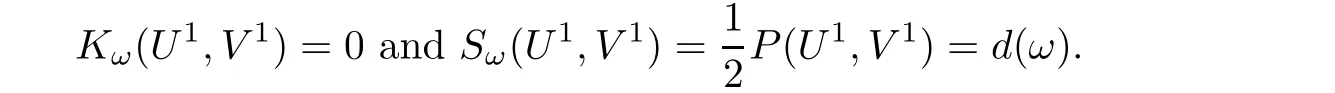
This shows that(U1,V1)is a minimizer for d(ω).The proof is complete.

Lemma 2.4Mω? Gω.

ProofLet(φ,ψ)∈ Mω.As Kω(φ,ψ)=0,we have Hω(φ,ψ)=3P(φ,ψ).On the other hand,as(φ,ψ)is a minimizer for d(ω),there exists a Lagrange multiplier γ ∈ R such that

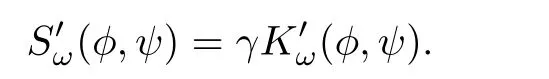
This implies that

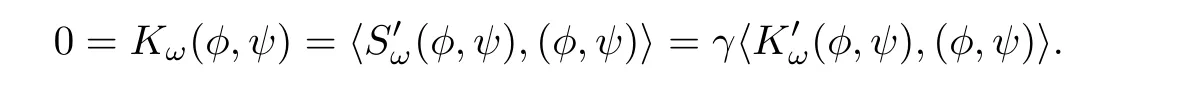
A direct computation shows that

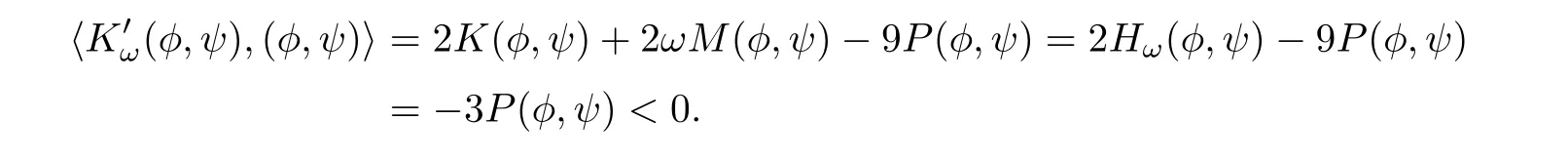
Lemma 2.5

ProofLet(φω,ψω) ∈ Gω.Because Mωis not empty,we take(φ,ψ) ∈ Mω.From Lemma 2.4,we have(φ,ψ) ∈ Gω.Thus,Sω(φω,ψω)=Sω(φ,ψ)=d(ω).It remains to show thatThis implies that

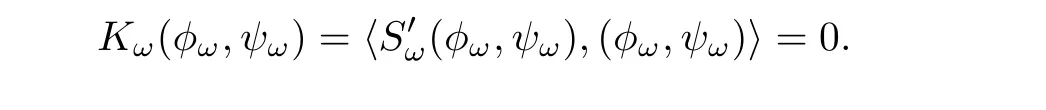
The proof is complete.

Proof of Proposition1.4 The proof of Proposition 1.4 follows immediately from Lemmas 2.3,2.4,and 2.5.

3 Strong Instability of Standing Waves

We are now able to study the strong instability of standing waves for(1.6).Note that the local well-posedness in H1×H1for(1.6)in 5D is given in Proposition 1.2.Let us start with the following so-called Pohozaev’s identities.

Lemma 3.1Let d=5,,and ω >0.Let(φω,ψω)∈ H1×H1be a solution to(1.7).Then,the following identities hold,

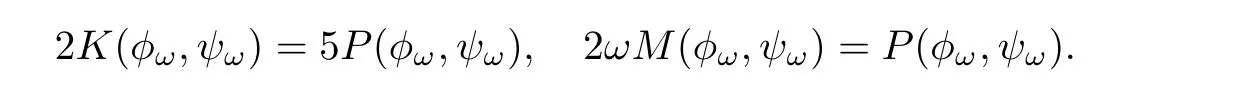
ProofWe only make a formal calculation.The rigorous proof follows from a standard approximation argument.Multiplying both sides of the first equation in(1.7)with,integrating over R5,and taking the real part,we have

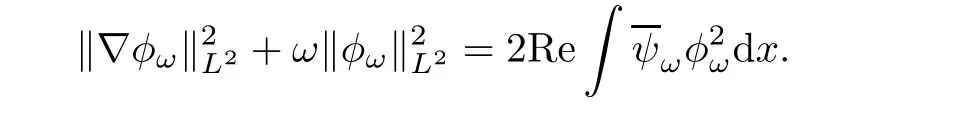
Multiplying both sides of the second equation in(1.7)withintegrating over R5,and taking the real part,we get

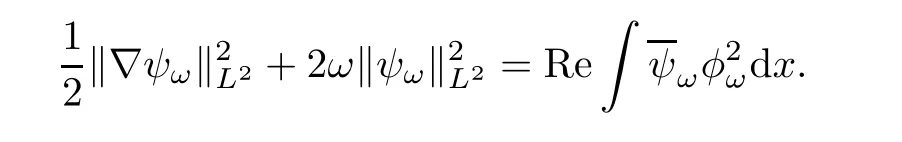
We thus obtain

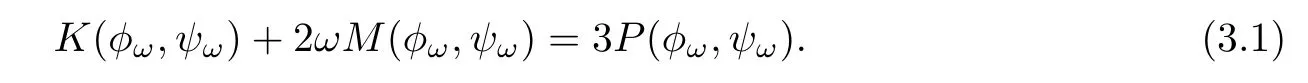
Multiplying both sides of the first equation in(1.7)withintegrating over R5,and taking the real part,we see that

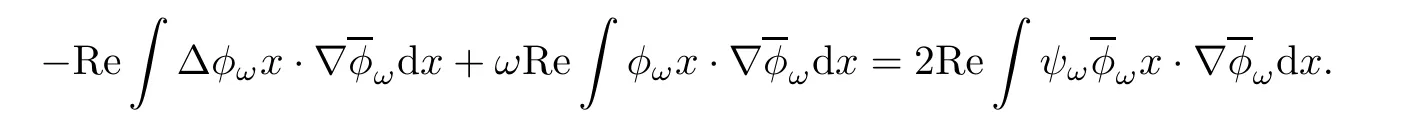
A direct computation shows that

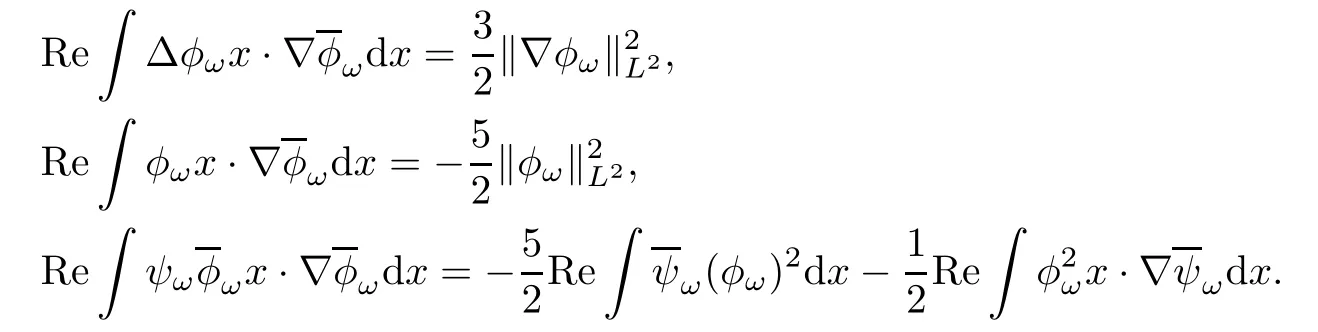
It follows that

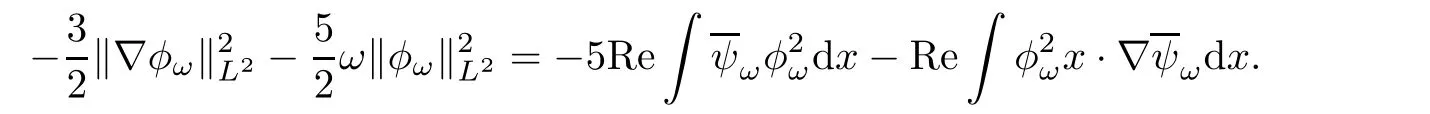
Similarly,multiplying both sides of the second equation in(1.7)withintegrating over R5,and taking the real part,we have

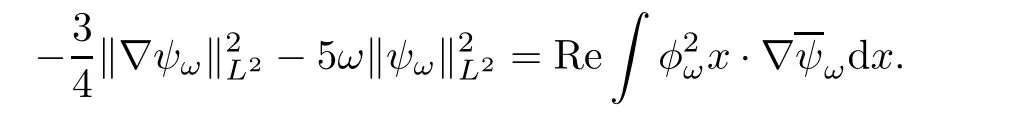
We thus get

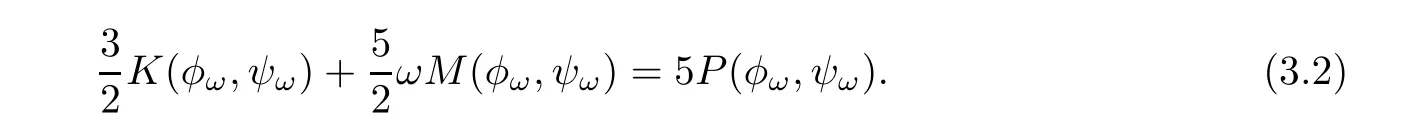
Combining(3.1)and(3.2),we prove the result.

We also have the following exponential decay of solutions to(1.7).

Lemma 3.2Let d=5,and ω >0.Let(φω,ψω)∈ H1×H1be a solution to(1.7).Then,the following properties hold:

? (φω,ψω)∈ W3,p× W3,pfor every 2 ≤ p< ∞.In particular,(φω,ψω)∈ C2× C2andas|x|→ ∞ for all|β|≤ 2;

?

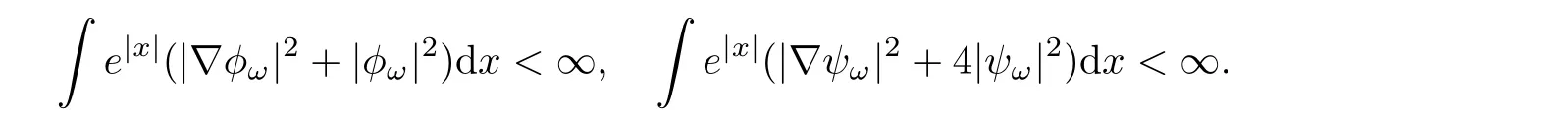
ProofWe follow the argument of[1,Theorem 8.1.1].Let us prove the first item.We note that if(φω,ψω) ∈ Lp× Lpfor some 2 ≤ p< ∞,thenIt follows thatBy Sobolev embedding,we see that

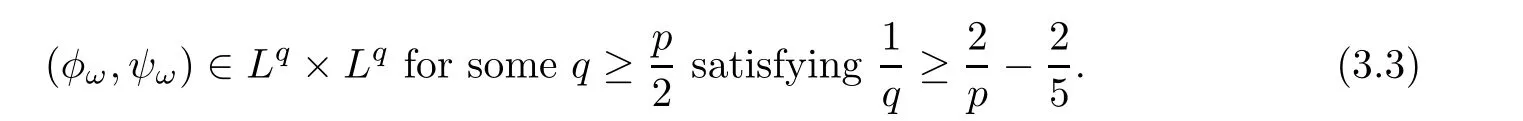
We claim that(φω,ψω)∈ Lp× Lpfor any 2 ≤ p< ∞.As(φω,ψω)∈ H1× H1,the Sobolev embedding implies that(φω,ψω)∈ Lp× Lpfor anyIt remains to show the claim for any p sufficiently large.To see it,we define the sequence

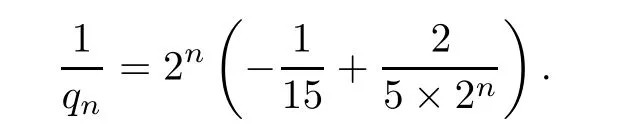
We have

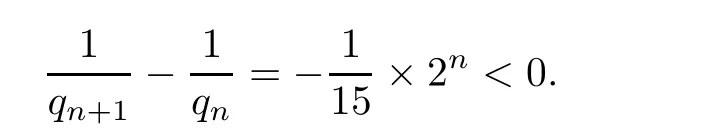
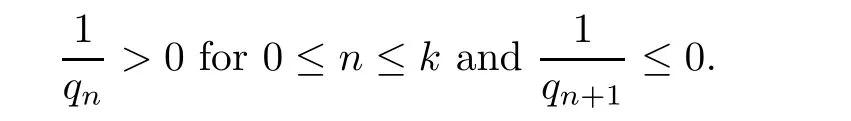
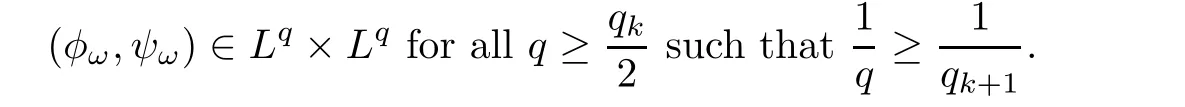
This shows that(φω,ψω)belongs to Lp× Lpfor any p sufficiently large.The claim follows.Using the claim,we have in particularfor any 2 ≤ p< ∞.Hence,(φω,ψω) ∈W2,p× W2,pfor any 2 ≤ p< ∞.By H?lder’s inequality,we see thatfor any 2 ≤ p< ∞ and any 1 ≤ j≤ 5.Thus,for any 2 ≤ p< ∞and any 1≤ j≤ 5,or(φω,ψω)∈ W3,p×W3,pfor any 2≤ p< ∞.By Sobolev embedding,(φω,ψω)∈ C2,δ×C2,δfor all 0< δ<1.In particular,for all|β|≤ 2.

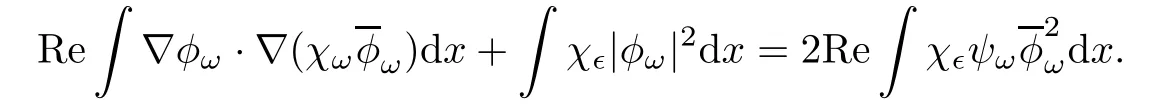
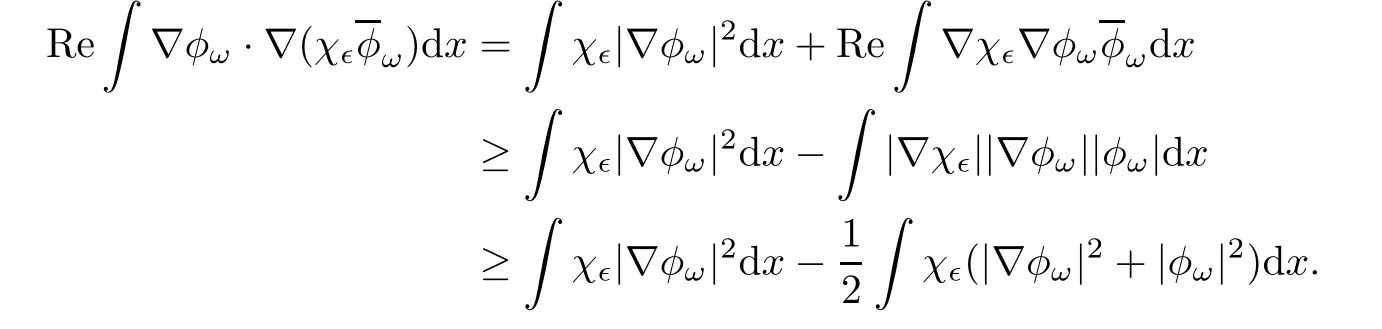
We thus get

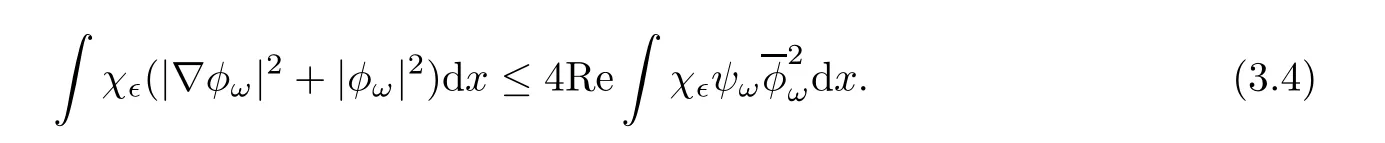
Similarly,multiplying both sides of the second equation in(1.7)withintegrating over R5,and taking the real part,we get

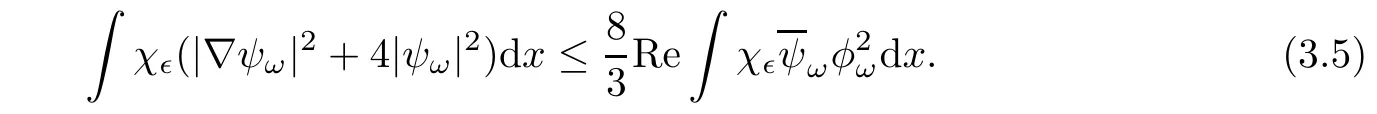
By the first item,there exists R>0 large enough such thatfor|x|≥ R.We have

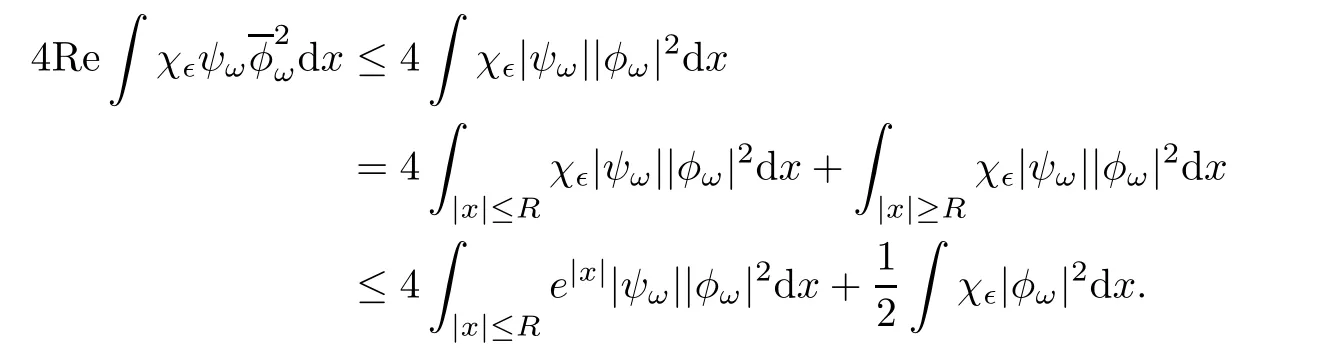
We thus get from(3.4)

Letting ?→ 0,we obtain

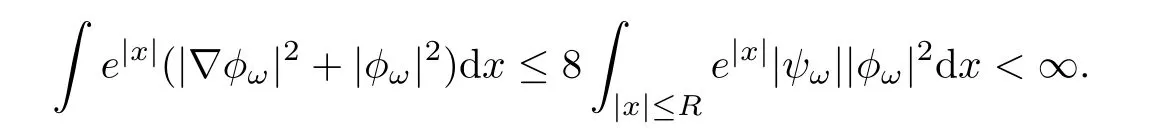
Similarly,by(3.5)and(3.6),

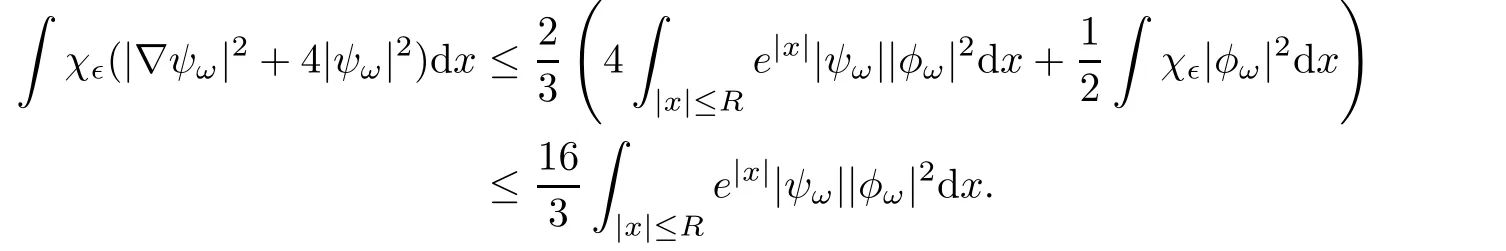
Letting ?→ 0,we get

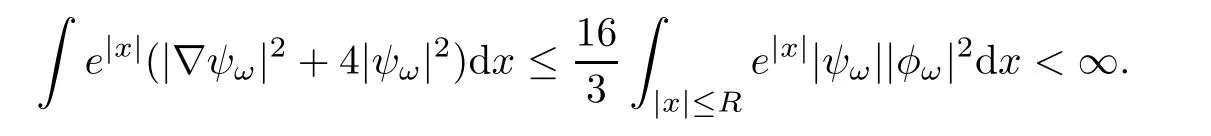
The proof is complete.

We also need the following virial identity related to(1.6).

Lemma 3.3Let d=5 andLet(u0,v0)∈H1×H1be such thatL2×L2.Then,the corresponding solution to(1.6)with initial data(u(0),v(0))=(u0,v0)satisfies

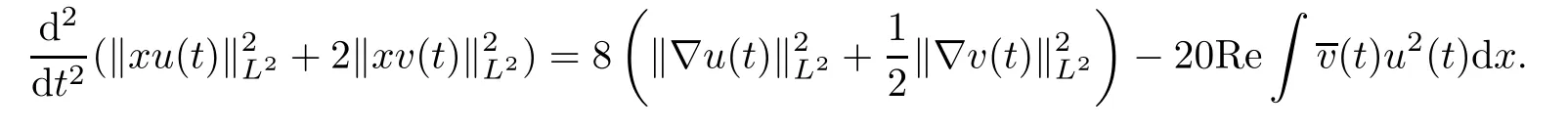
ProofThe above identity follows immediately from[4,Lemma 3.1]with

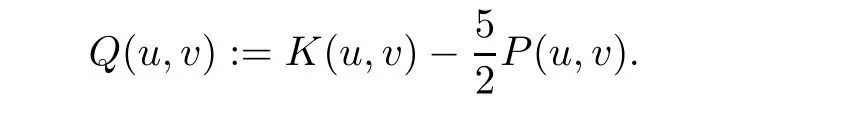
It is obvious that

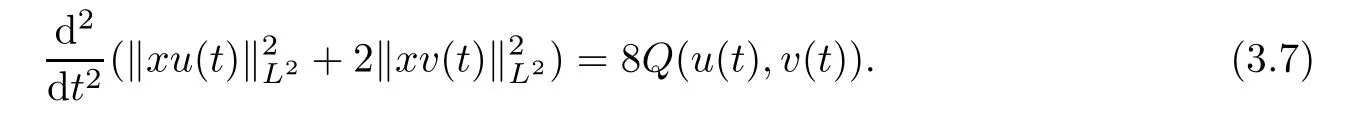
Note that if we take

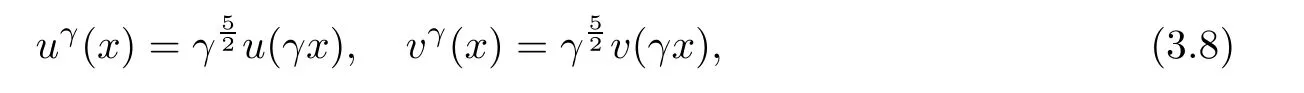
then

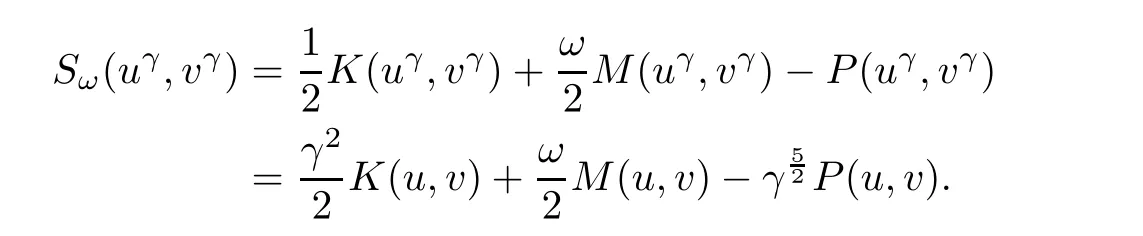
It is easy to see that

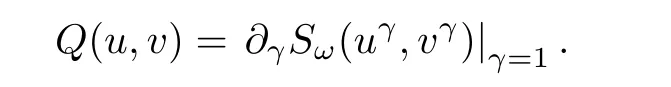
Lemma 3.4Let d=5,and ω >0.Let(φω,ψω)∈ Gω.Then,

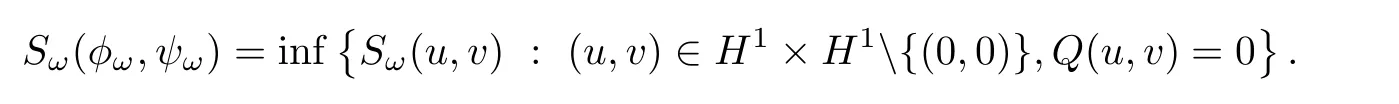
ProofDenote

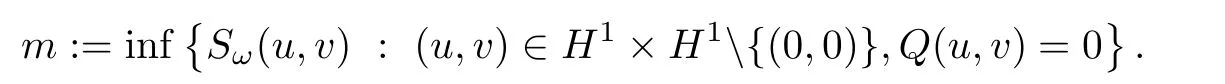
As(φω,ψω)is a solution of(1.7),it follows from Lemma 3.1 that Q(φω,ψω)=Kω(φω,ψω)=0.Thus,

Now,let(u,v)∈ H1× H1{(0,0)}be such that Q(u,v)=0.If Kω(u,v)=0,then by Proposition 1.4,Ifwe consider Kω(uγ,vγ)= γ2K(u,v)+where(uγ,vγ)is as in(3.8).Asandthere exists γ0>0 such that.It again follows from Proposition 1.4,On the other hand,

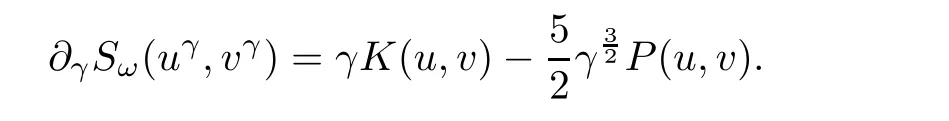
We see that the equation ?γSω(uγ,vγ)=0 admits a unique non-zero solution

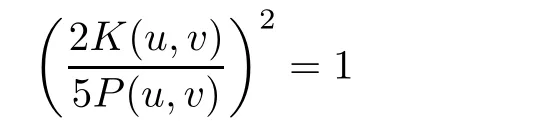
because Q(u,v)=0.This implies thatif γ ∈ (0,1)andif γ ∈ (1,∞).In particular,for all γ >0.Hence,We thus obtainfor any(u,v)∈ H1×H1{(0,0)}satisfying Q(u,v)=0.Therefore,

Combining(3.9)and(3.10),we prove the result.

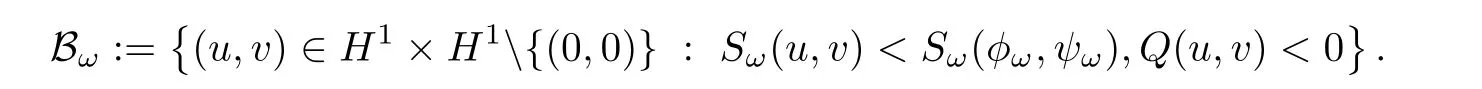
Lemma 3.5Let d=5,ω >0,and.The set Bωis invariant under the flow of(1.6).

ProofLet(u0,v0)∈ Bω.We will show that the corresponding solution(u(t),v(t))to(1.6)with initial data(u(0),v(0))=(u0,v0)satisfies(u(t),v(t))∈Bωfor any t in the existence time.Indeed,by the conservation of mass and energy,we have

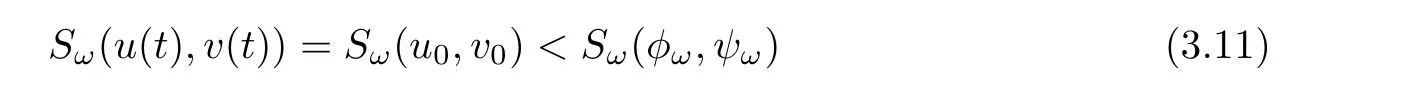
for any t in the existence time.It remains to show that Q(u(t),v(t))<0 for any t as long as the solution exists.Suppose that there exists t0>0 such that Q(u(t0),v(t0))≥0.By the continuity of the function t 7→ Q(u(t),v(t)),there exists t1∈ (0,t0]such that Q(u(t1),v(t1))=0.It follows from Lemma 3.4 that Sω(u(t1),v(t1))≥ Sω(φω,ψω),which contradicts to(3.11).The proof is complete.

Lemma 3.6Let d=5,ω >0,and(φω,ψω)∈ Gω.If(u,v)∈ Bω,then

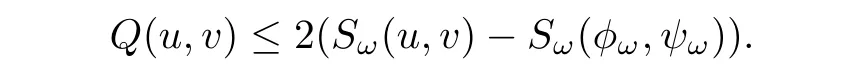
ProofLet(u,v)∈ Bω.Set

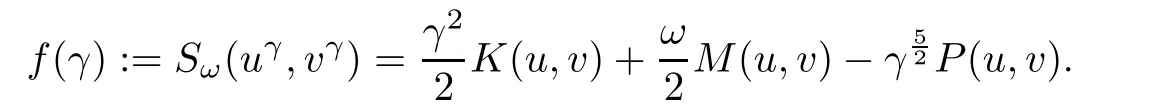
We have

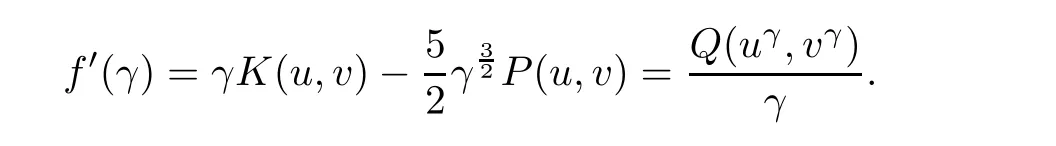
We see that

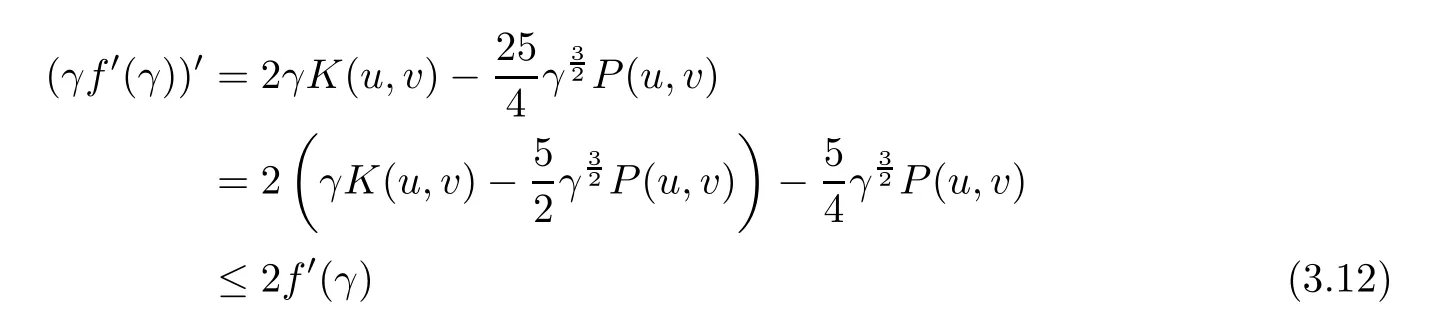
for all γ >0.Note that P(u,v)≥ 0,which follows from the fact Q(u,v)<0.We also note that as Q(u,v)<0,the equationadmits a unique non-zero solution

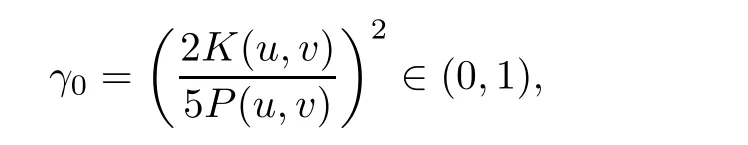
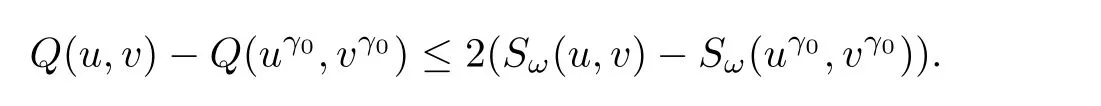
The result then follows from the fact thatas

We are now able to prove the strong instability of standing waves given in Theorem 1.6.

Proof of Theorem1.6Let ?>0.Becauseas γ →1,there exists γ0>1 such thatWe claim that.Indeed,we have

As Q(φω,ψω)=0,the equationadmits a unique non-zero solution

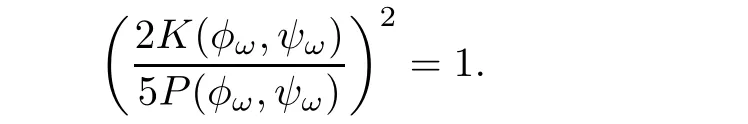
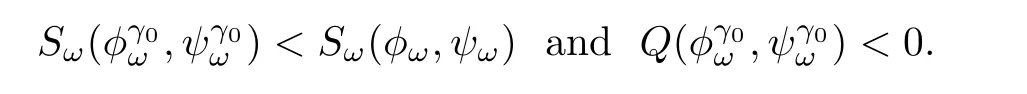
By the local well-posedness,there exists a unique solution(u(t),v(t))∈C([0,T),H1×H1)to(1.6)with initial data(u(0),v(0))=where T>0 is the maximal time of existence.By Lemma 3.5,we see that(u(t),v(t))∈Bωfor any t∈[0,T).Thus,applying Lemma 3.6,we get

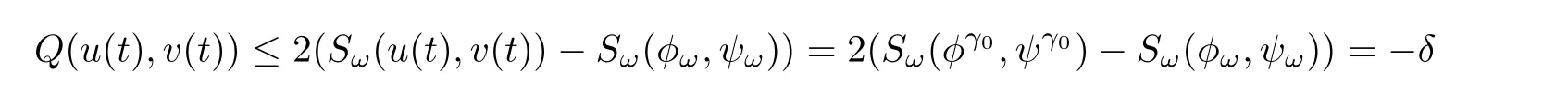
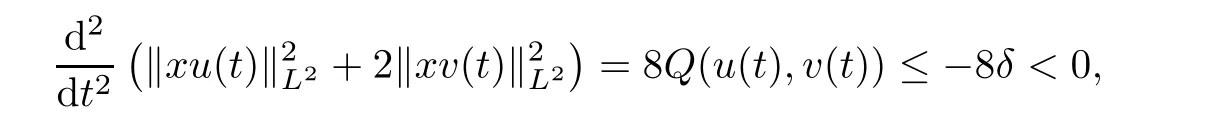
for any t∈[0,T).The classical argument of Glassey[5]implies that the solution blows up in if nite time.The proof is complete.

AcknowledgementsThis work was supported in part by the Labex CEMPI(ANR-11-LABX-0007-01).The author would like to express his deep gratitude to his wife-Uyen Cong for her encouragement and support.