縱振型低頻壓電水聽器的等效電路及有限元分析對比研究

徐言哲，范桂芬，田豐，鄧皓元，胡洪平，呂文中

縱振型低頻壓電水聽器的等效電路及有限元分析對比研究

徐言哲，范桂芬，田豐，鄧皓元，胡洪平，呂文中

(華中科技大學光學與電子信息學院，湖北武漢 430074)

分別利用等效電路理論與ANSYS有限元仿真對縱振型復合棒式壓電水聽器的性能參數進行了計算，并將兩種結果進行比對分析。對比發現兩種分析方法得出的接收靈敏度最大值對應的頻率不在同一處并且在數值上存在一定差異，在遠離諧振點的較低頻段，水聽器的接收靈敏度都具有較為平坦的響應。等效電路理論只考慮了一維縱向振動并且將模型完全理想化，而ANSYS有限元分析則考慮了整個結構的縱向橫向模態耦合，其建模更接近實際模型，因此ANSYS有限元分析在水聽器的仿真優化設計中更符合實際情況，但還需制作實物，用實測結果進行比對。等效電路理論由于物理意義明顯，可以為水聽器設計和有限元仿真提供理論指導。

等效電路理論；ANSYS有限元仿真；接收靈敏度

0 引言

水聲換能器是發射和接收水中聲信號的裝置，是進行水聲學研究的核心設備，其性能好壞直接影響水聲設備的性能[1]。水聲換能器按其工作狀態的不同，可以分為兩類：把電磁能轉化成聲能的一類稱為發射器，把聲能轉化為電磁能的一類稱為接收器，也稱為水聽器[2]。PZT(鋯鈦酸鉛)作為壓電陶瓷的一種，其機電耦合系數高、壓電常數大、穩定性好，常被用來作為制備壓電水聽器的換能元件。目前高低頻壓電水聽器的應用都較為廣泛，但關于低頻縱振型壓電水聽器，尤其是其在次聲波范圍的研究和應用較少。

地震、海嘯、核爆及火山噴發都會產生次聲波，次聲波傳播時衰減小，傳播距離遠。水下地震監測，海嘯預報、核爆檢測及火山噴發等領域都急需低頻、寬帶、高靈敏度的水聽器[3-6]。因此，低頻水聽器具有極其重要的研究意義。常用的壓電水聽器結構為縱振復合棒式結構，人們在分析該換能器的工作模式及器件性能時常采用兩種方法：一為等效電路法，即將器件等效為理想的阻容元件[7]，二為采用有限元建模分析法，國內多位學者進行了研究[8]。但這兩種方法由于計算方法和建模的不同，分析結果會有一定的差別。因此本文分別利用等效電路理論和ANSYS有限元仿真，對縱振型復合棒式水聽器的性能參數進行理論計算并且進行對比，希望得到一些今后能指導水聽器設計計算的有益結論。

1 利用等效電路理論分析縱振復合棒式水聽器的性能參數

縱振復合棒式水聽器的結構圖如圖1所示，將縱振復合棒式水聽器看作由前蓋板、壓電晶堆、后蓋板3部分組成的機械振動體，忽略了預應力螺栓，由波動理論得出機械振動方程，根據邊界條件求解，再由壓電方程和機電類比的方法，建立等效電路。

圖1 縱振復合棒式水聽器結構示意圖

等效電路理論的優點是能夠直觀表達物理意義，結構參數及材料參數能直觀體現在數學表達式中[7]。由上述方法，分別得到縱振復合棒式水聽器前蓋板、壓電晶堆、后蓋板3部分的等效電路圖，再將三者串聯，得到最終的等效電路圖[2]，如圖2所示，圖中A、B、C三個虛線框中分別為后蓋板、壓電晶堆、前蓋板的分塊等效電路。

圖2 縱振復合棒式水聽器的等效電路圖

圖2中各阻抗表達式如下[2]：

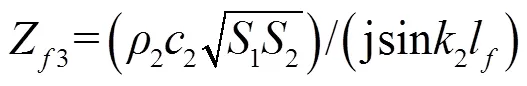
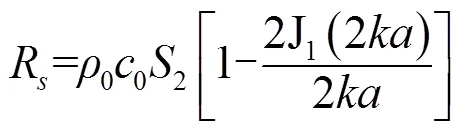
數學表達式(1)～(9)及圖2中各參數含義如下：

一階貝塞爾函數：

一階斯特魯夫函數：

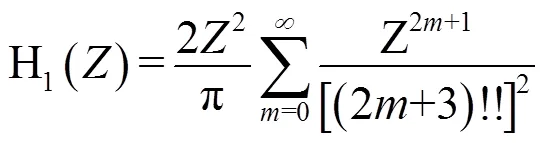
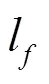
由接收靈敏度定義計算靈敏度：

令：

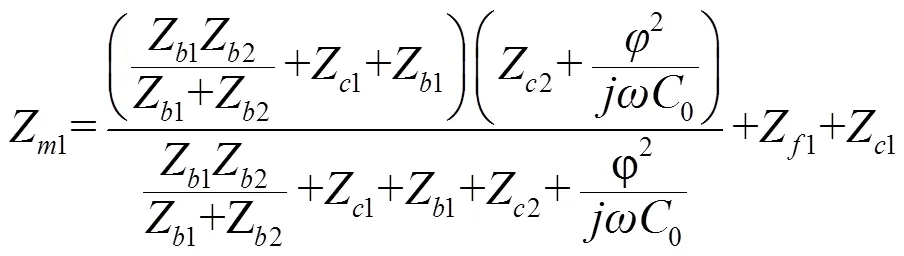
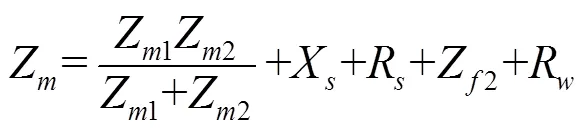
則

再代入式(12)、(13)，最后利用式(19)[2]：

代入材料參數和幾何尺寸并利用Matlab軟件對上述公式進行數值計算，可得到接收靈敏度曲線，如圖3所示。

接收靈敏度的最大值約為-170.7 dB，在200～10 800 Hz頻段內，接收靈敏度起伏小于等于3 dB。

可得到該模型的導納曲線，分別取實部虛部得到電導G、電納B。利用Matlab作圖得到電導電納曲線。如圖4所示，本理論模型在有輻射阻抗以及輻射面加載水的情況下，一階縱振頻率大概在20 750 Hz處，最大電導值為0.711 mS。

2 利用ANSYS有限元分析縱振復合棒式水聽器的性能參數

ANSYS是目前較為流行的有限元仿真軟件，在水聽器的設計上，該軟件提供了多種單元類型，用于分析結構應力、壓電、多物理場耦合等[8]。

ANSYS在處理結構力學線性問題時所依賴的有限元方程如下：

2.1 模態分析

本文利用ANSYS對縱振復合棒式水聽器進行模態分析，這里只給出在短路恒壓狀態和開路恒流狀態下的模態分析結果，如圖5所示。圖5表明了縱振復合棒式水聽器的一階縱向諧振模態振型和一階縱向反諧振模態振型。

為計算方便，模態分析只建立了二分之一軸對稱模型，主要包括前蓋板、壓電晶堆、后蓋板、螺栓4個部分。材質分別選用硬鋁、PZT-5H、不銹鋼、45#鋼。壓電晶堆和金屬部分賦予的單元類型分別為Plane 42和Plane 13。壓電晶堆的材料參數包括介電常數矩陣、剛度矩陣、壓電應力常數矩陣及密度。金屬部分材料參數包括密度、泊松比和楊氏模量。

由模態分析計算得到，縱振復合棒式水聽器一階縱向諧振頻率與一階縱向反諧振頻率分別為20 370.1 Hz和26 810.4 Hz。考慮到工程實際情況，水聽器的接收靈敏度最大值應該在反諧振頻率附近，如果需要其工作頻率在較低頻段并且保證接收靈敏度曲線足夠平坦，其工作頻率的上限保守估計應不大于反諧振頻率的1/3。由模態分析得到的一階縱向反諧振頻率，可粗略地將諧響應分析的頻率范圍定為0～40 000 Hz。

圖5 縱振復合棒式水聽器一階縱向諧振模態與一階縱向反諧振模態

2.2 諧響應分析

建立水中的有限元模型，將六片壓電片正極和負極上的所有節點各定義一個耦合部，即電壓耦合，使正極或負極上的所有節點電勢相同，并在正極與負極上分別施加1 V與0的電壓載荷。在前蓋板與近水場接觸面施加流固耦合界面。水中有限元模型如圖6所示。

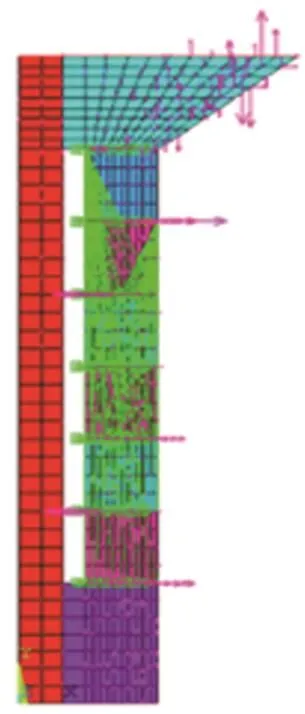
圖6 水聽器有限元模型

從圖7中可看出接收靈敏度最大值約為-170.5 dB。觀察較低頻段，曲線一定程度上保持平坦，大約在200~5200 Hz頻段內，接收靈敏度起伏小于等于3 dB。

在水中做諧響應分析，可分析出水聽器的導納特性并與等效電路法相比較。在壓電晶堆表面正極與負極分別定義電壓耦合部，并在正極與負極上分別施加1 V與0的電壓載荷，求解后提取正極耦合部序號最低節點上的電荷，在時間后處理中求出電導電納曲線。在水中的電導電納曲線如圖8所示。此外，還得到水聽器在水中的電阻電抗曲線，如圖9所示。

圖7 基于ANSYS仿真得到的接收靈敏度曲線

從水中的電導電納曲線(圖8)可知，電導最大值約為0.80 mS，此處的頻率即為一階縱向諧振頻率,約為20 600 Hz。根據圖9，電阻電抗曲線只展現出水聽器在水中的一階反諧振特性，當電阻()取極大值時，該點所處頻率對應水聽器的接收靈敏度曲線的峰值所處頻率，即一階縱向反諧振頻率。觀察電抗()，存在一個波峰和一個波谷，波峰對應的頻率為，波谷對應的頻率為，與水聽器接收靈敏度反諧振頻率處的-3 dB帶寬大致吻合。通過觀察與，說明接收靈敏度曲線和阻抗曲線在峰值段趨勢差不多。

圖8 基于ANSYS仿真的換能器在水中的電導、電納曲線

圖9 基于ANSYS仿真的換能器在水中的電阻、電抗曲線

3 對比與分析

通過對比接收靈敏度曲線(圖3與圖7)，發現通過等效電路理論與基于ANSYS仿真得到的接收靈敏度最大值分別為-170.7 dB和-170.5 dB，它們對應的頻率分別約為23 100 Hz和27 400 Hz，有15.7%的誤差。考慮兩者帶內起伏小于3 dB，分別在200～10 800 Hz與200～5 200 Hz頻段內有較為平坦的響應。對比導納特性(圖4與圖8)，兩種方法得到的電導最大值以及所對應的一階縱向諧振頻率存在微小差異，一階縱向諧振頻率分別約為20 750 Hz與20 600 Hz。

造成上述差異的原因可能為：

(2) 等效電路理論只考慮水聽器一維縱向振動，忽略了其它模態。但通過有限元分析(見圖5)可看出，水聽器不僅有縱向振動，還包含前蓋板、壓電晶堆、螺栓的彎曲振動，考慮了整個結構體的縱向橫向振動耦合。

(3) 有限元分析中，水聽器前蓋板與近水場接觸面施加了流固耦合界面，而等效電路理論中并未考慮此因素。

(4) 等效電路理論中，水聽器的輻射阻抗是理論計算的結果。有限元分析中，諧響應分析中輸入的阻尼系數只是經驗值，對于實際環境必然存在誤差。無論是等效電路理論還是有限元分析，對于水聽器的工作環境都進行了理想化。

4 結論

本文通過以上分析，得到以下結論：

(1) 等效電路理論只考慮一維縱向振動，將結構件等效為實心體。該水聽器模型通過計算接收靈敏度和導納特性發現，接收靈敏度最大值約為170.7 dB，對應的頻率約為23 100 Hz，接收靈敏度在200～10 800 Hz頻段內起伏≤3 dB。

(2) 利用ANSYS有限元仿真，由模態分析得到水聽器的一階縱向諧振頻率與一階縱向反諧振頻率分別為203 70.1 Hz和268 10.4 Hz，計算導納特性，電導最大值所在頻率與一階縱向諧振頻率相同，由諧響應分析得到的接收靈敏度曲線在一階縱向反諧振頻率附近存在峰值，約為-170.5 dB。大約在200～5 200 Hz頻段內，接收靈敏度曲線起伏小于3 dB。當電阻()取極大值時，該點所處頻率對應水聽器的接收靈敏度曲線的峰值所處頻率，即一階縱向反諧振頻率。此外，電抗曲線中波峰波谷對應的頻率之間的帶寬與水聽器接收靈敏度反諧振頻率處的-3 dB帶寬大致吻合。

(3) 由等效電路理論和ANSYS有限元仿真得到的接收靈敏度最大值對應的頻率分別在231 00 Hz和27 400 Hz處，有15.7%的誤差，并且接收靈敏度在數值上存在差異。兩種方法計算出的導納曲線中，一階縱向諧振頻率分別約為20 750 Hz與20 600 Hz。

[1] 莫喜平. 功能材料及其應用于換能器技術的研究進展[J].物理, 2009; 38(3): 149-156

MO Xiping. Functional materials and their research progress in transducer technology[J]. Physics, 2009, 38(3): 149-156.

[2] 周福洪. 水聲換能器及基陣[M]. 北京: 國防工業出版社, 1984: 7-8, 63-72

ZHOU Fuhong. Hydroacoustic transducer and array[M]. Beijing: National Defence Industry Press, 1984: 7-8, 63-72.

[3] WORCESTER P F. Deep-water ocean acoustic propagation: observations[J]. J. Acoust. Soc. Am., 2015, 138(3): 1842.

[4] WUNSCH C. Ocean acoustic tomography: past, present, and maybe future[J]. J. Acoust. Soc. Am., 2015, 138(3): 1818.

[5] WALKER D A. Deep ocean seismology[J]. Eos, Transactions American Geophysical Union, 1984, 65(1): 2-3.

[6] SONG H C. Diversity combining for long-range acoustic communication in deep water using a towed array[J]. J. Acoust. Soc. Am., 2012, 132(2): 68-73.

[7] 桑永杰. 低頻寬帶水聲換能器研究[D]. 哈爾濱: 哈爾濱工程大學, 2014: 34.

SANG Yongjie. Low frequency broadband underwater acoustic transducer research[D]. Harbin: Harbin Engineering University. 2014: 34.

[8] 莫喜平. ANSYS軟件在模擬分析聲學換能器中的應用[J]. 聲學技術, 2007, 26(6): 1280-1290.

MO Xiping. Application of ANSYS software in simulation analysis of acoustic transducer[J]. Acoustic Technology, 2007, 26(6): 1280-1290.

[9] 何作鏞, 趙玉芳. 聲學理論基礎[M]. 北京: 國防工業出版社, 1981: 245-246, 329-332

HE Zuoyong, ZHAO Yufang. Acoustic theory foundation[M]. Beijing: National Defense Industry Press, 1981: 245-246, 329-332.

[10] 劉爽. 新型矢量水聽器研究[D]. 哈爾濱: 哈爾濱工程大學, 2016: 65.

LIU Shuang. New vector hydrophone research[D]. Harbin: Harbin Engineering University, 2016: 65.

Comparative research on equivalent circuit and finite element analysis of longitudinal vibration type low-frequency piezoelectric hydrophones

XU Yan-zhe, FAN Gui-fen, TIAN Feng, DENG Hao-yuan, HU Hong-ping, LYU Wen-zhong

(The School of Optical and Electronic Information, Huazhong University of Science & Technology,Wuhan 430074, Hubei, China)

The equivalent circuit theory and ANSYS Finite Element Simulation are used to calculate the performance parameters of longitudinal vibration type composite rod piezoelectric hydrophone, and the two calculation results are compared. It is shown that the resonant frequencies of the receiving sensitivity obtained by the two methods are not in the same place, and there are some differences in the value of receiving sensitivity, and that the bandwidths of receiving sensitivity are all rather wide in the lower frequency band far from the resonance point. It is known that the equivalent circuit theory only considers the one-dimensional longitudinal vibration and idealizes the model. However, the ANSYS finite element analysis considers the longitudinal and transverse modal coupling of the whole model structure, which is closer to the actual model. Therefore, ANSYS has more advantages in the simulated optimization design of hydrophone. The equivalent circuit theory can provide theoretical guidance for finite element simulation because of its obvious physical significance.

equivalent circuit theory; ANSYS finite element simulation; reception sensitivity

TB565.1

A

1000-3630(2019)-06-0710-06

10.16300/j.cnki.1000-3630.2019.06.019

2018-05-31;

2018-06-28

中央高校基本科研專項資金，華中科技大學(2016JCTD114)

徐言哲(1995－), 男, 湖北宜昌人, 碩士研究生, 研究方向為水聲換能器與有限元仿真。

呂文中, E-mail: lwz@hust.edu.cn