基于最大胸徑生長率的浙江省杉木人工林立地質量評價

楊海賓， 張茂震， 丁麗霞， 于曉輝

（ 1. 浙江農林大學 省部共建亞熱帶森林培育國家重點實驗室， 浙江 杭州311300； 2. 浙江農林大學 環境與資源學院， 浙江 杭州311300）

森林立地質量評價是實現科學造林、 合理高效利用林地的重要保證。 掌握森林立地質量可為森林的可持續發展制定更科學的經營措施及提高森林的經濟、 生態、 社會效益提供理論基礎［1］。 傳統的森林立地質量評價采用的是地位指數或地位級作為重要指標， 即根據林分優勢木的平均高和林分平均高2 種直接評價方法評定立地質量［1-3］。 雖然這2 種方法在同齡林的質量評價中精度較高， 但需要進行大量的實地調查、 采伐并制作解析木， 導致經濟成本和生態成本較高， 永久性樣地和代表性試驗樣地缺乏， 因而傳統森林立地質量評價所需的大尺度數據相對缺乏［3-4］， 實用性較差。 隨著近年來遙感技術應用于立地質量的評價研究［5-6］， 大尺度的立地分類逐漸克服了傳統森林立地質量評價中生境制圖時的耗時、 耗人力的缺點。 此外， 統計學方法用于森林立地質量評價和分類的實踐也取得了良好效果， 如聚類分析、 多元回歸分析、 數量化理論［7-12］等各種統計方法的應用使得定量研究在立地分類和立地質量評價綜合系統的構建中有了更廣泛的空間［9-14］。 然而， 盡管這些方法可以增加森林立地質量評價和分類結果的經濟產出， 并在一定條件下提高精度， 但他們基本上仍沿用傳統的評價指標， 在成本與效益之間沒有突出改善， 難以適應大范圍森林立地質量評價［15-17］。 國家森林資源連續清查數據是覆蓋范圍廣、 精度可靠的數據， 但在較大范圍的森林立地評價研究應用卻非常少， 相關案例主要是結合遙感影像以樣地總生物量為評價指標。 而樣地總生物量會受年齡、 人為活動等多種干擾因素的影響， 難以準確評價森林立地質量。本研究利用近期5 期浙江省國家森林資源清查（national forest inventory， NFI）樣地數據， 提取杉木Cunninghamia lanceolata林樣地優勢木的最大胸徑生長率， 作為備選立地質量評價指標， 結合數字高程模型（DEM）和土壤數據， 運用數量化理論Ⅰ方法建立浙江省杉木人工林立地質量評價數量化理論模型。

1 研究區概況與研究數據

1.1 研究區概況

浙江省地處中國東南沿海長江三角洲南翼， 屬亞熱帶季風氣候， 季風顯著， 四季分明， 年氣溫適中， 光照較多， 雨量豐沛， 空氣濕潤， 雨熱季節變化同步， 氣候資源類型多樣， 氣象災害繁多。 年平均氣溫15.0～18.0 ℃， 年平均降水量為980～2 000 mm， 年平均日照時數1 710～2 100 h。

全省陸域面積為1 055×104hm2， 其中山地和丘陵占74.6%。 全省林地面積667.97×104hm2， 森林面積584.42×104hm2（其中85.95×104hm2為國家特別規定灌木林）； 杉木人工林純林面積96.74×104hm2， 占森林面積的19.43%。 全省大部分地區適宜杉木生長， 南部屬于杉木中心產區。

1.2 研究數據

1.2.1 立地因子數據 立地因子（包括地形地貌、 土壤、 氣候、 植被、 生物等）對樹木的生長有重要影響。 坡度、 坡向、 海拔、 土壤、 坡位、 濕度、 太陽輻射等地形及環境因素會不同程度影響杉木的生長［18-19］，其中地形因子主要包括海拔、 坡位、 坡向、 坡度等。 濕度及太陽輻射由于數據較難獲取［20］， 本研究考慮其與地區所在的緯度關系較大， 因此將緯度列為立地因子之一。 地形因子可由DEM 處理得到， 浙江省DEM 由地理空間數據云網站上下載得到。 DEM 提取緯度、 海拔、 坡位、 坡向、 坡度等信息在Arc GIS軟件中完成。

1.2.2 樣地數據 浙江省1989-2009 年共5 期NFI 樣地數據， 包括樣地和樣木數據。 由于浙江省在1989 年后有部分樣地位置移動， 1989 年清查數據僅作分析參考用， 實際應用為1994-2009 年共4 期數據。 4 期NFI 樣地數據中， 有連續復位樣木的杉木人工林樣地529 個， 用于建模； 另有用于模型檢驗的臨安地區2004-2009 年杉木林固定樣地51 個。 所有樣地數據包含樣地編號、 樣地位置、 行政區、 地理地貌信息、 土壤信息和樣地內植被信息等。 樣木數據包含樣地編號、 樣木編號、 樹種、 胸徑等。 由于樣地是固定（永久）的， 樣地號和樣木號在不同調查期是固定的， 因而可實現每株樣木生長的連續監測。

2 研究方法

2.1 基于數量化理論Ⅰ的立地質量評價模型

數量化理論Ⅰ是一種類似多元回歸的分析方法［15-16］， 用于自變量都是定性變量、 基準變量是定量變量的因素分析與預測問題， 采用說明性多變量模擬線性表示式中基準變量的定量變化。 假定有如下的線性模型：

假設自變量中有h個是定量的， 它們在第i個樣本中的數據為xi（u）（u=1, 2,…,n）， 有m個是定性的，即m個項目， 其中第j項目有rj個類目， 它們在第i個樣本中的反應式基準變量的數據為yi（i=1,2, …,n）。

利用最小二乘法， 即Bu（u=1,2, …,h）和bjk（j=1,2, …,m;k=1,2, …,rj）的最小二乘估計構造正規方程：

求解正規方程組（2）得預測方程, 并對方程精度進行檢驗， 同時通過偏相關系數、 方差比和范圍評價每個立地因子對因變量作用的大小。

數量化理論Ⅰ相對于一般回歸分析， 其不同之處在于可把定性變量與定量變量同時納于回歸模型。在數量化理論模型中， 因變量和自變量被分別稱為基準變量和說明變量。 說明變量中定性變量稱為項目， 每個定性變量的劃分稱為類目， 定性變量的類目類似于定量變量的取值區間。

2.2 立地因子的量化

根據數據易采集、 便于立地質量評價模型推廣的原則， 參考前人研究成果， 選擇立地因子。 本研究選取影響杉木生長的地形因子與土壤類型作為立地因子。 地形因子包括地貌、 緯度、 海拔、 坡度、 坡向、 坡位等， 其中緯度、 海拔、 坡度是定量變量， 地貌、 坡向、 坡位與土壤類型是定性變量。 根據數量化理論Ⅰ對變量的約定， 結合樣地立地因子數據， 對定性立地因子進行類目劃分（表1）， 并對項目（因子）的類目利用示性函數（0, 1）數量化方法對定性因子進行定量化處理， 即：

將每個樣地的定性因子代入式（3）中， 與定量因子一起編制立地因子數量化反應表（表2）， 用于立地質量模型建立與評價。

2.3 立地質量評價指標確立

反映森林立地質量最主要和直接的指標是生產力。 可觀測的森林立地生產力指標主要有特定年齡的樹高、 胸徑和蓄積量， 或者其生長量， 應用最多的是特定年齡的優勢木樹高。 然而， 優勢木樹高和年齡的準確測量不僅成本很高， 而且難度特大。 胸徑生長率是最能直觀反映立地質量的森林立地質量評價因子。 現有的NFI 數據信息量豐富， 且數據可靠性好。 胸徑是NFI 調查中最為重要的測樹因子， 但在NFI中不調查單株樣木的年齡。 從NFI 中提取的胸徑生長率只能代表在某一清查期內某棵樹胸徑的年均生長率， 并不能直接反映所在地段的立地質量好壞。 為了充分利用NFI 數據開展森林立地質量評價， 本研究提出1 個新的立地質量評價指標： 最大胸徑生長率指標。 以最大胸徑生長率指標為立地評價指標， 與地形地貌、 環境、 土壤等易獲取因子建立模型， 可以用于估計包含無林地在內的所有林地的潛在生產力。一般來說， 林木的生長規律是從幼齡林到成熟、 過熟林， 胸徑和樹高的生長速度都呈逐漸降低的趨勢，即在樹木的生長過程中生長率都會出現一個高峰。 因此， 在NFI 清查次數足夠多的情況下,每個樣地復位樣木的生長率都會在某一時期出現最高值， 即最大胸徑生長率， 它代表了該地塊的最大生產潛力。 若以R表示最大胸徑生長率， 則：

式（4）中：k為清查期，rk為第k期的胸徑生長率，n為森林資源清查總期數。

表1 定性立地因子類目劃分與量化編號Table 1 Classification and quantitative numbering of qualitative site factors

表2 立地因子反應表Table 2 Response table of site factors

NFI 清查間隔期為5 a， 杉木的齡級期也是5 a， 5 期NFI 清查數據即可覆蓋5 個齡級期的生長率。假定杉木輪伐期為25 a， 近熟林進入成熟林時全部采伐， 則5 次清查能包含全部最大胸徑生長率。 因此， NFI 與齡級之間的關系如圖1 所示。 圖1 中， 樣地樣木的齡級為Ⅰ～Ⅴ， 成熟林全部采伐（由于現實森林的林齡不同， 因而有A、 B、 C、 D、 E 等5 種情形）。

樣木胸徑生長率的計算方法如下：

式（5）中：rijk為第i個樣地、 第j株復位樣木、 第k期清查的胸徑生長率；Dij（k+1）為k+1 期樣木胸徑；Dijk為第k期樣木胸徑。

樣地胸徑生長率計算建立在樣木生長率的基礎上， 設第i個樣地、 第k期清查的胸徑生長率為rik， 則：

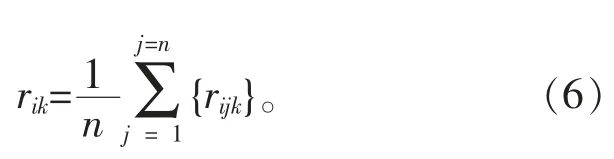
樣地優勢木生長率比樣地生長率更能代表樣地所在位置的立地生產潛力， 樣地優勢木胸徑生長率計算公式如下：

式（7）中： rikD即第i樣地第k期3 株優勢木生長率的均值。

根據樣地的胸徑生長率， 從每個樣地多期調查數據所生成的胸徑生長率時間系列中選取最大者：

式（8）中：riD相當于樣地i位置幼齡林優勢木的平均胸徑生長率。

圖1 清查期次與樣木齡級分布Figure 1 Inventory period and age class distribution of sample trees

2.4 立地質量評價精度檢驗

2.4.1 模型顯著性檢驗 復相關系數是估計回歸精度的重要指標之一， 復相關系數越大， 則估測相關越密切， 說明模型對優勢木最大胸徑生長率均值的估計效果越好， 所得的數量化得分表就越可靠［21］。 根據復相關系數檢驗線性關系是否顯著進行F檢驗， 可確定坡位、 坡向、 土壤類型、 緯度位置、 海拔、 坡度等變量的線性關系是否顯著［22］。

2.4.2 模型預測精度檢驗 模型預測精度檢驗采用均方根誤差（RMSE）作為模型的評價指標。 均方根誤差是用來衡量實際測量值同模型預測值之間的偏差， 它可作為衡量測量精度的一種數值指標［23］。 在模型建立后， 為對模型擬合性能進行檢驗， 運用浙江省杭州市臨安區的實際測量值代入模型計算最大胸徑生長率進行實地檢驗， 采用平均絕對誤差、 RMSE 值進行評估， 反映模型估測的精度。

2.4.3 方差比檢驗模型檢驗 采用方差比方法進行。 該檢驗方法具有精確的樣本分布， 而不依賴于大樣本漸近極限分布； 在通常的時間序列數據非正態分布的情況下， 這種非參數方差比檢驗具有更高的檢驗功效。 方差比檢驗對于一段時間內某一時間間隔的方差比例效果較好。 方差比檢驗是指各因子（項目）方差占模型方差的百分比， 表示立地因子（坡位、 坡向、 土壤類型、 緯度位置、 海拔、 坡度）對因變量（最大胸徑生長率）的作用是否顯著。

3 結果與分析

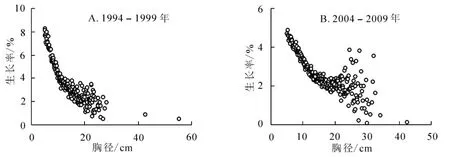
圖2 杉木單株生長率比較Figure 2 Comparison of growth rate of C. lanceolata

3.1 基于NFI 的立地質量評價指標

3.1.1 單株胸徑生長率與胸徑的關系 根據NFI 數據分析， 杉木生長率從幼林到成熟林呈下降趨勢。 圖2A 和圖2B 顯示了1994-1999 年和2004-2009 年調查間隔期內杉木單株生長率按胸徑分布的變化。 首先， 胸徑生長率隨胸徑增大而降低， 2 個時期趨勢相同。 其次， 其趨勢為單調下降。 再次， 曲線在縱軸上分布較寬， 特別是當胸徑大約為20～30 cm 時， 生長率出現較大的變化范圍。 圖2B（2004-2009 年）最為明顯。 它們代表了多條單調下降的曲線， 其本質是不同立地質量的生長率差異。 這一特點圖2B 較圖2A 突出， 原因是2004 年這有部分位置移動后的新樣地加入。 2 幅圖同時顯示， 隨著胸徑增大， 其生長率分化明顯， 而在較小胸徑階段生長率隨胸徑增大而較快下降， 且在縱軸上分布區間較窄。

3.1.2 單株胸徑生長率隨時間變化趨勢 單株胸徑生長率連續變化趨勢與年齡有關。 在無年齡的情況下， 這種變化在連續多期之間呈單調曲線形式上升或下降。 圖3 為單株木胸徑生長率隨胸徑增長而的變化情況。 為了圖示清晰，將每個胸徑值所對應的多株樣木胸徑生長率取均值， 每條曲線代表1 個胸徑級。 圖3 中D8 代表第1 次清查時胸徑為8 cm， D12 代表第1 次清查時胸徑為12 cm， ……。 余類推。 從圖3 可以發現： 小徑級樣木胸徑生長率大， 大徑級樣木胸徑生長率小。 以后一直保持這一規律。 對于同一株樣木來說， 清查次數增加就是年齡的增加， 隨著年齡的增長， 樣木胸徑生長率下降， 最后趨于平緩。 結果表明： 在杉木生長過程中， 單株胸徑生長率存在最大值， 這個最大值代表所在地段的森林立地生產力。 因此， 最大胸徑生長率可以被用作森林立地質量評價的直接指標。

3.1.3 樣地最大胸徑生長率 通過多期復位樣木分析， 提取每個樣地的最大胸徑生長率。 由于樣地采伐、 災害等因素影響， 用樣地全部樣木胸徑生長率的平均值代表樣地生產潛力的狀態不適合所有樣地。 表3 顯示： 用3 株最大胸徑生長率取平均與樣地的立地因子有更好的相關性。 因此， 為了避免偶然因素的干擾， 每個樣地的最大胸徑生長率取3 棵優勢木胸徑生長率的均值。共提取529 個樣地的最大胸徑生長率。

圖3 杉木不同胸徑徑級平均生長率隨時間變化趨勢Figure 3 Trend of average growth rate of different DBH grades of C. lanceolata with time

表3 最大胸徑生長率與立地因子之間皮爾森相關系數Table 3 Pearson correlation coefficient between the maximum DBH growth rate and the site factor

3.2 杉木林立地質量評價模型

以優勢木最大胸徑生長率均值作為因變量， 坡位、 坡向、 土壤類型、 緯度位置、 海拔、 坡度作為自變量， 采用數量化理論Ⅰ建立杉木林立地質量評價模型。 4 期529 個NFI 的樣地數據參與數量化擬合，運用軟件SPSS 19.0 完成線性回歸分析模型建立與評價。 具體結果見表4。

根據表4 數據， 本研究最終建立浙江省杉木林立地質量評價預測模型公式為：

式（9）中： δ（1）為樣地緯度位置， δ（2）為樣地海拔， δ（3）為樣地坡度， δ（4,i）為樣地坡位第i個項目， δ（5,i）為樣地坡向第i個項目，δ（6,i）為樣地土壤類型第i個項目。 表4 顯示模型統計檢驗F=14.723， 達極顯著水平， 模型復相關系數R為0.606。 方差分析（表5）表明： 各項目對模型貢獻均達顯著水平。

3.3 模型檢驗

3.3.1 方差比檢驗 方差比是各因子（項目）方差占模型方差的百分比， 表示因子對因變量（最大胸徑生長率）的作用是否顯著。 按公式計算各影響因素的方差， 結果見表5。 結果表明： 對胸徑生長率的貢獻程度從大到小依次是坡向、 坡位、 土壤類型、 坡度、 緯度、 海拔。 其中坡向對杉木林胸徑生長率的貢獻率最大， 坡向會影響太陽光照量和太陽輻射強度， 造成不同坡向的日照強度和熱量不同， 從而對杉木林的生長產生較大影響。 坡位對杉木林的胸徑生長率的貢獻率較大， 不同坡位具有相應的小氣候環境， 影響著濕度、 水分和溫度等條件。 土壤類型對胸徑生長率的貢獻同樣較大的原因是由于土壤類型不同， 杉木生長的土壤營養環境不同， 從而對杉木林的生長產生一定影響。 從表4 和表5 可以看出： 緯度和海拔的影響較小， 主要是因為本研究所選擇的研究區為浙江省， 緯度變化范圍較小； 同時浙江省內山地平均海拔一般在200～1 000 m， 而本研究杉木人工林樣地分布在400～800 m 較窄的范圍內， 兩者的差距對于杉木林來說不能形成較大區分度， 因此緯度和海拔的對于胸徑生長率的貢獻率較小。

3.3.2 基于臨安實地數據的模型擬合精度分析 在模型建立后， 為對模型擬合性能進行檢驗， 運用浙江省杭州市臨安區的實際測量值代入模型計算最大胸徑生長率進行實地檢驗， 采用平均絕對誤差、 RMSE值進行評估， 對全部樣本和臨安地區樣本的觀測值和預測值之間的誤差進行評價， 反映模型估測的精度。 從表6 可以看出： 臨安地區樣本和全部樣地作為模型估計結果檢驗的平均絕對誤差分別為3.407 和2.125， 整體平均絕對誤差相對較小， 而且隨著樣本的增加， 模型的擬合精度提高， 表明利用最大生長率進行數量化理論擬合是精度相對較高的方法。 均方根誤差能夠反映預測值和測量值之間的偏差程度，數據顯示臨安區樣本和全部樣本檢驗的均方根誤差為0.518 和1.421， 而計算兩者的相對均方根誤差的值分別為0.073 和0.062， 相對均方根誤差越小， 相對均值的離散程度越小， 模型的精度也就越高。

表4 杉木林立地因子數量化理論Ⅰ得分及t 檢驗表Table 4 Score and t-test table of the quantification theory Ⅰmodel of C. lanceolata

表5 各類立地因子影響因素方差比Table 5 Variance ratio of the influencing factors of various site factors

表6 模型擬合誤差分析表

4 結論與討論

基于NFI 的最大胸徑生長率是杉木人工林立地質量評價的可靠指標， 在經濟上節約、 高效。 從建模因子的貢獻率來看， 對胸徑生長率的貢獻程度從大到小依次是坡向、 坡位、 土壤類型、 坡度、 緯度、 海拔。 利用最大胸徑生長率， 結合DEM 數據建立數量化理論Ⅰ模型， 模型擬合效果和檢驗結果均比較理想。 在缺乏樹齡和樹高數據的情況下， 可以利用基于多期NFI 數據的樣地最大胸徑生長率作為評價指標進行森林立地質量評價。 不僅可以用于現有杉木人工林立地質量評價， 還可以用于無林地立地生產潛力預測。

本研究提出基于NFI 的最大胸徑生長率作為杉木人工林立地質量評價指標， 結合地理信息建立立地質量評價模型， 結果符合研究區內杉木林生長立地條件現狀。 但限于研究區NFI 數據積累的時間跨度有限， 模型精度還有進一步提高的空間。 由于NFI 每5 a 清查1 次， 其數據的時間分辨率為5 a。 因此，NFI 清查期數越多， 在同一個樣地所測樣木的年齡階段越多， 從中提取的最大胸徑生長率對相應立地生產力的代表性越接近真實。 隨著NFI 數據的不斷積累， 基于NFI 的森林立地質量評價精度會不斷提高。同時， 基于數量化理論Ⅰ的杉木最大胸徑生長率估計模型所解決的問題是得到所有森林立地上的假設最大胸徑生長率， 只是一個以生長率代表立地質量的初步展現， 在此基礎上還可以有進一步的分類、 聚類及其檢驗等分析。