兆瓦級直驅永磁同步風力發電機系統研究

林 立，何 洋，周建華，陳鴻蔚

(1.邵陽學院 多電源地區電網運行與控制湖南省重點實驗室，邵陽 422000；2.邵陽學院 信息工程學院，邵陽 422000； 3.湘潭電機集團有限公司，湘潭 411100)

0 引 言

海上直驅永磁同步風力發電機(以下簡稱PMSWG)因清潔、高效、高可靠性，備受各國學者青睞[1]；但兆瓦級電機系統性能要求高、硬件研制與調試成本高，亟待研究如何將電機設計與控制優化有機融合，以提升發電機效率，抑制諧波輸出[2]。

近年來，針對電機設計與優化，文獻[3-4]通過研究不同工況與功率下永磁發電機的電磁設計及參數對其性能影響，得出鐵心長度、極弧系數、氣隙長度與永磁體厚度對發電機齒槽轉矩及其諧波、損耗與電磁轉矩的影響規律。文獻[5-10]基于結構與尺寸參數對電機效率與轉矩、齒槽轉矩及其諧波性能影響規律，利用單變量、多目標耦合尋優得到使發電機性能最佳的氣隙長度、永磁體厚度與極弧系數、斜槽寬度與斜極結構；但其性能受結構和大量尺寸參量耦合影響[11]。針對該問題，本文基于電機相似性及其性能分析，提出利用多變量、多目標耦合研究斜極/斜槽結構的360 kW/690 V,200 r/min永磁同步發電機的尺寸參量優化，以提升發電機效率與轉矩，削弱齒槽轉矩與諧波。

針對電機高性能控制，文獻[12]基于永磁發電機線性模型研究了機側系統雙閉環PI控制結構及其參數整定；但PI控制模型依賴性較強[13]，兆瓦級風電調試成本高、研制周期長。針對該問題，本文提出利用有限元法精確建立電機模型，利用場路耦合仿真模擬發電機在四種不同風速擾動、電磁耦合影響參數攝動共同作用下的動態起動過程，驗證了系統實現最大功率追蹤的可行性。

1 發電機優化設計與分析

1.1發電機尺寸參數優化

依據國家標準，高效、大轉矩，諧波畸變與齒槽轉矩小是決定PMSWG在全風速實現最大功率追蹤與柔性并網關鍵指標[14]。

電樞斜槽時，其齒槽轉矩[11]：

式中：La為鐵心長度；μ0為真空磁導率；Di1,D2為定子內徑與轉子外徑；θs0,θs1為定子槽寬與槽距的弧度值；δ為氣隙長度；hm為永磁體厚度；Br為永磁材料剩磁；p1為極對數；z為定子槽數；n為使nz/(2p)為整數的最小整數；αp為極弧系數；Nz為斜槽寬度。

電機損耗p與電磁轉矩Te[11]:

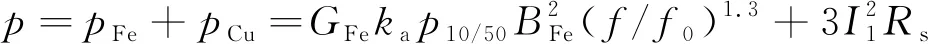
(2)

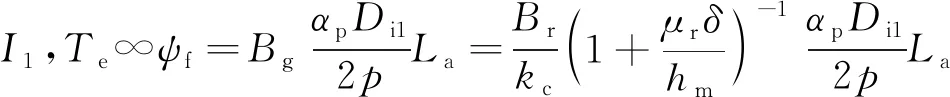
(3)

式中：pFe,pCu為鐵耗與銅耗；GFe為鐵心重量；ka為鐵耗經驗系數；p10/50為電磁材料比損耗；BFe為鐵心磁密；f,f0為發電機定子交流頻率與交流電頻率；I1為定子電流；Rs為相電阻；ψf為轉子磁鏈；Bg為氣隙磁密；kc為氣隙系數。

由式(1)～式(3)可見，發電機效率、轉矩受鐵心長度、極弧系數、氣隙長度、永磁體厚度、斜槽寬度等參數耦合的影響。因此可選鐵心長度、極弧系數、氣隙長度、永磁體厚度、斜槽寬度為優化變量，發電機的高效、大轉矩、齒槽轉矩與諧波畸變THD小為約束條件，研究參數對發電機性能影響，利用多變量、多目標耦合尋優，獲得使發電機性能最佳的尺寸參數。

1.1.1 鐵心長度對電機性能的影響

如表1所示，可由電機的幾何相似確定主要尺寸參數，由RMxprt設計永磁同步發電機，添加鐵心長度La=0.7～1.3 m優化方案，可得鐵心長度對電機齒槽轉矩與齒諧波、額定轉矩與損耗影響，如圖1、圖2所示。齒槽轉矩與鐵心長度成正比，適當增加鐵心長度可減少損耗，但有效轉矩削弱，且La=0.9 m時，損耗最小。

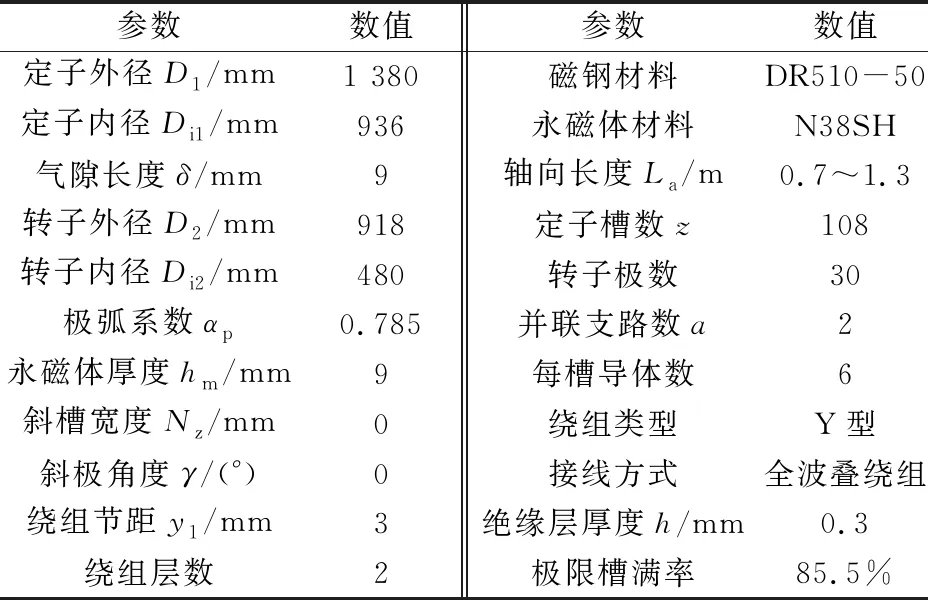
表1 360 kW/690 V，200 r/min PMSWG主要參數

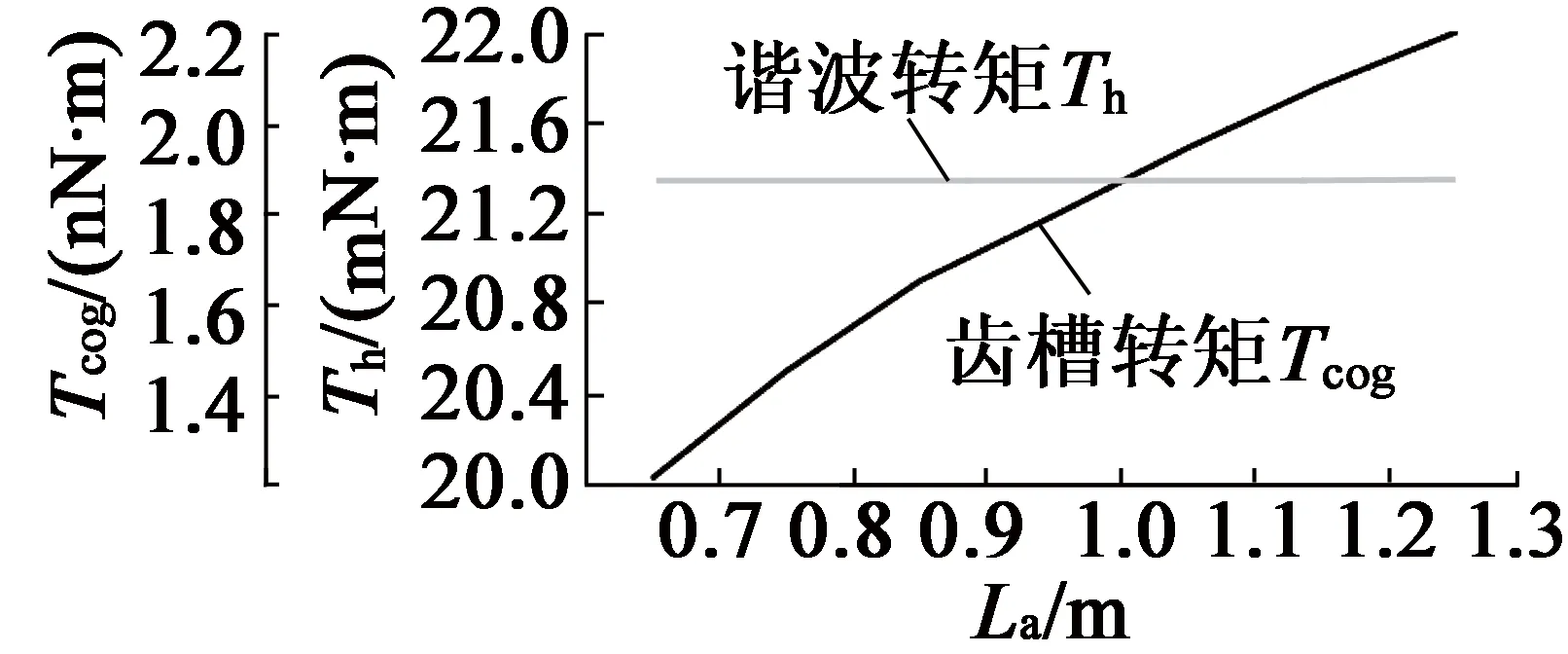
圖1 Tcog,Th與La關系曲線

圖2 Te,p與La關系曲線

1.1.2 極弧系數對電機性能的影響

由表1確定主要尺寸參數，并由上文確定最優的鐵心長度為0.9 m，由RMxprt設計永磁同步發電機，添加極弧系數αp=0.7～0.8優化方案，可得極弧系數對電機齒槽轉矩與齒諧波、電磁轉矩與效率的影響，如圖3、圖4所示。極弧系數與電磁轉矩、損耗成正比，與齒諧波成反比，且當αp=0.715，損耗最小；當αp=0.785，齒槽轉矩與齒諧波最小。

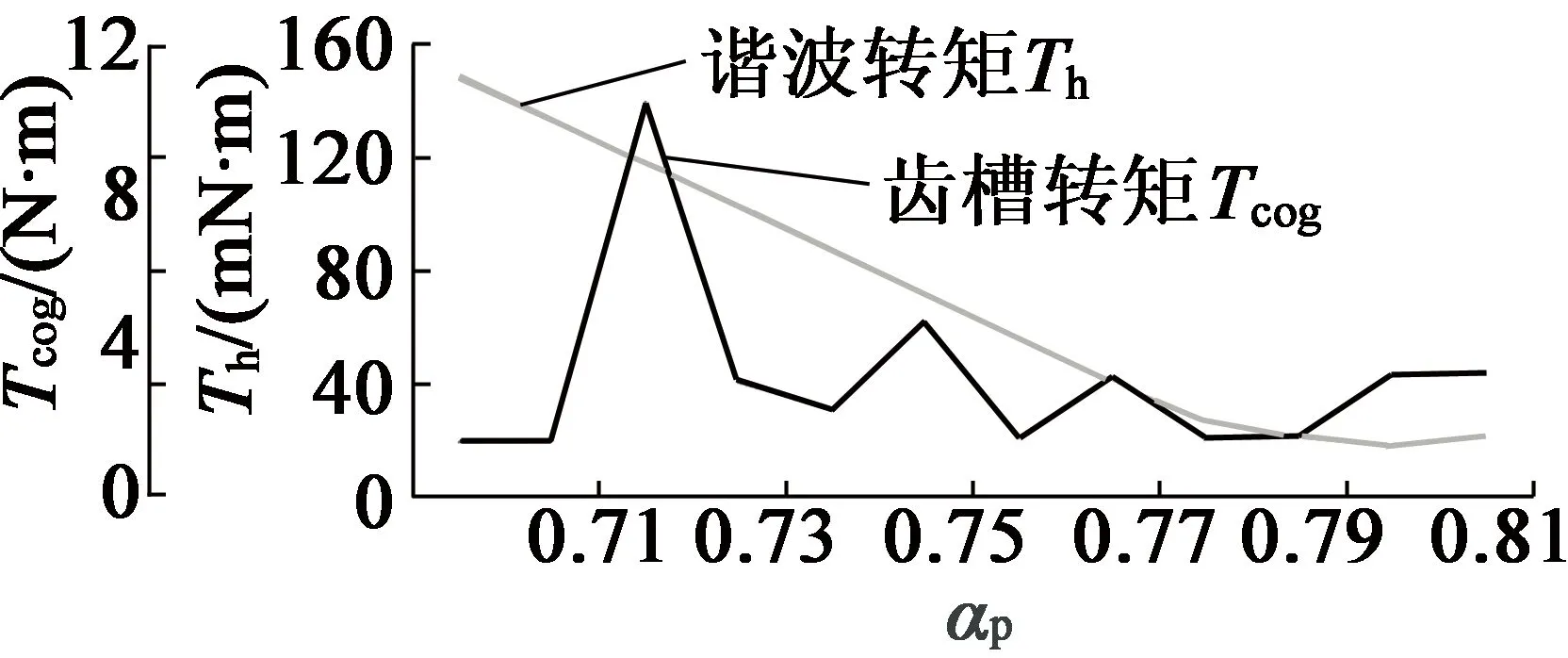
圖3 Tcog,Th與αp關系曲線

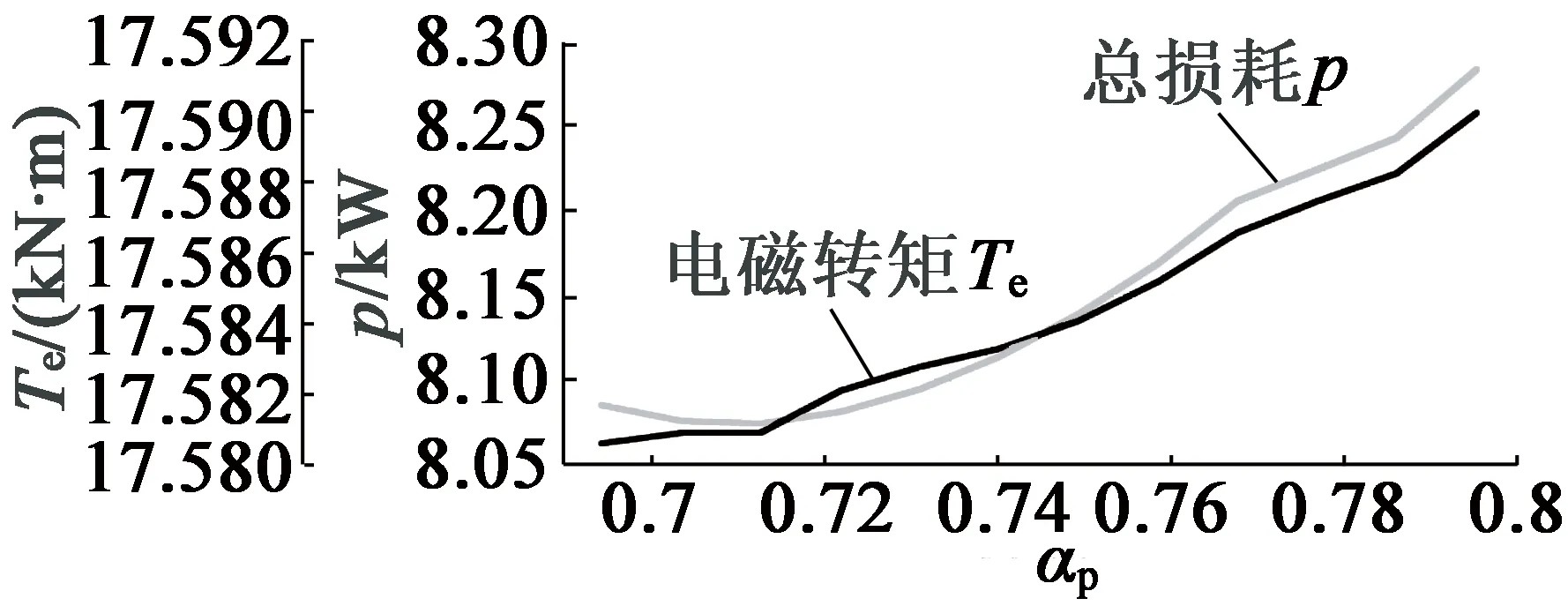
圖4 Te,p與αp關系曲線

1.1.3 氣隙長度對電機性能的影響

由表1確定主要尺寸參數，并由上文確定最優的鐵心長度為0.9 m與極弧系數為0.785，由RMxprt設計永磁同步發電機，添加氣隙長度δ=1～9 mm優化方案，可得氣隙長度對電機齒槽轉矩與齒諧波、電磁轉矩與效率影響，如圖5、圖6所示。氣隙長度與齒諧波成反比，適當增加氣隙長度可增加電磁轉矩，減少電機損耗，δ為9 mm或1 mm時，Tcog，Te與p基本一致，但齒諧波最小。

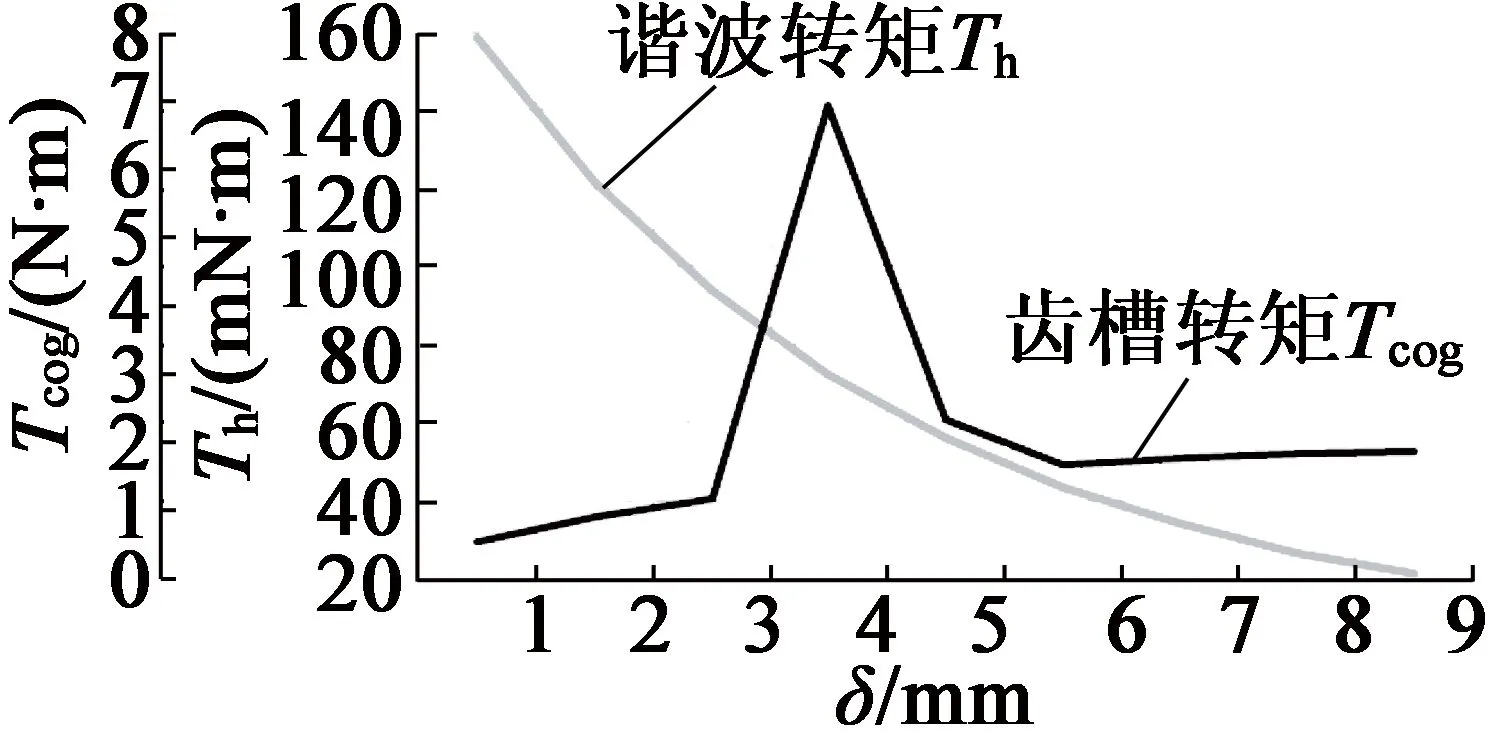
圖5 Tcog,Th與δ關系曲線

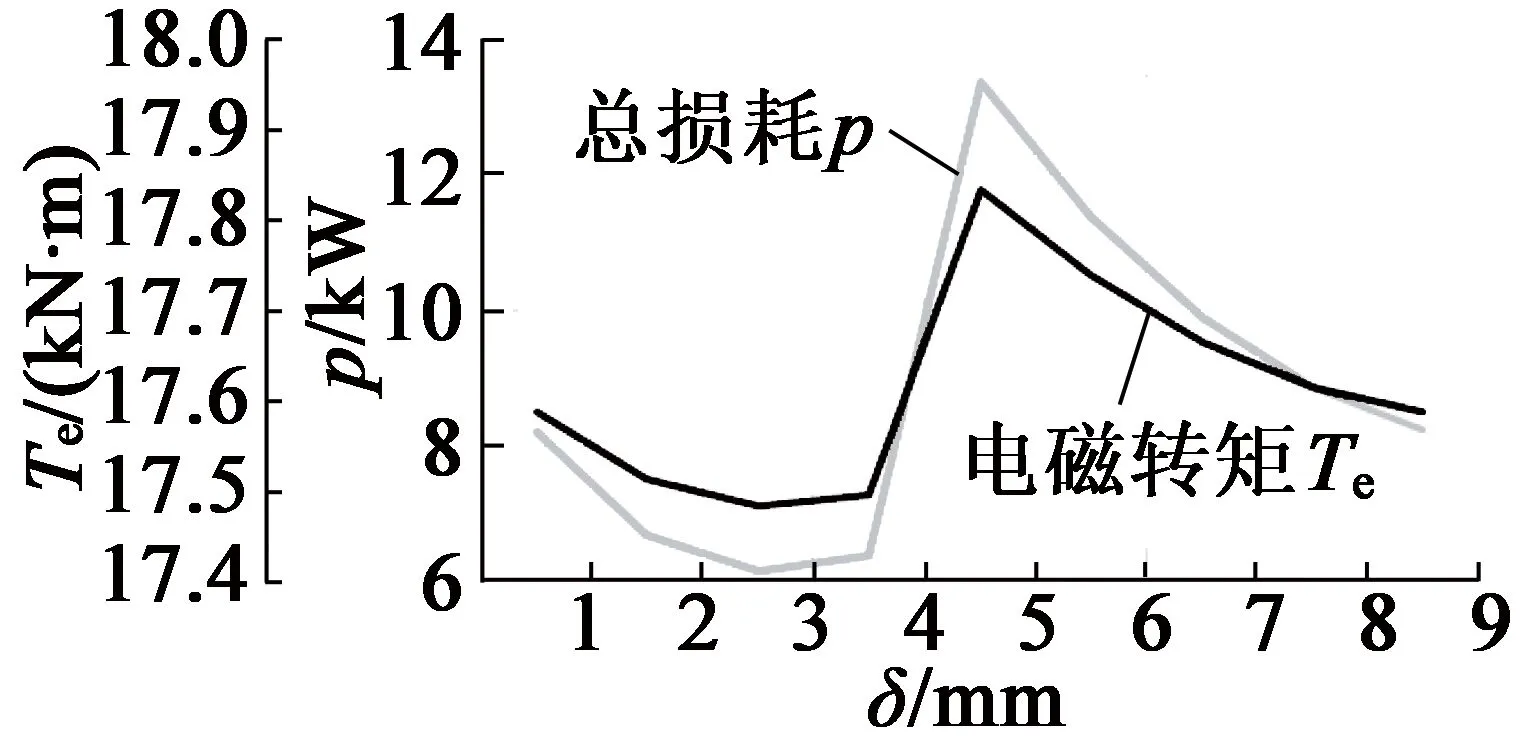
圖6 Te, p與δ關系曲線

1.1.4 永磁體厚度對電機性能的影響

由表1確定主要尺寸參數，并由上文確定最優的鐵心長度、極弧系數與氣隙長度分別為0.9 m，0.785與9 mm，由RMxprt設計永磁同步發電機，添加永磁體厚度hm=1～9 mm優化方案，永磁體厚度對電機齒槽轉矩與齒諧波、電磁轉矩與效率影響如圖7、圖8所示。永磁體厚度與齒諧波成反比，適當增加永磁體厚度可增加Te，hm為9 mm或1 mm時，Tcog基本一致，雖p增加，但Te最大，齒諧波最少。

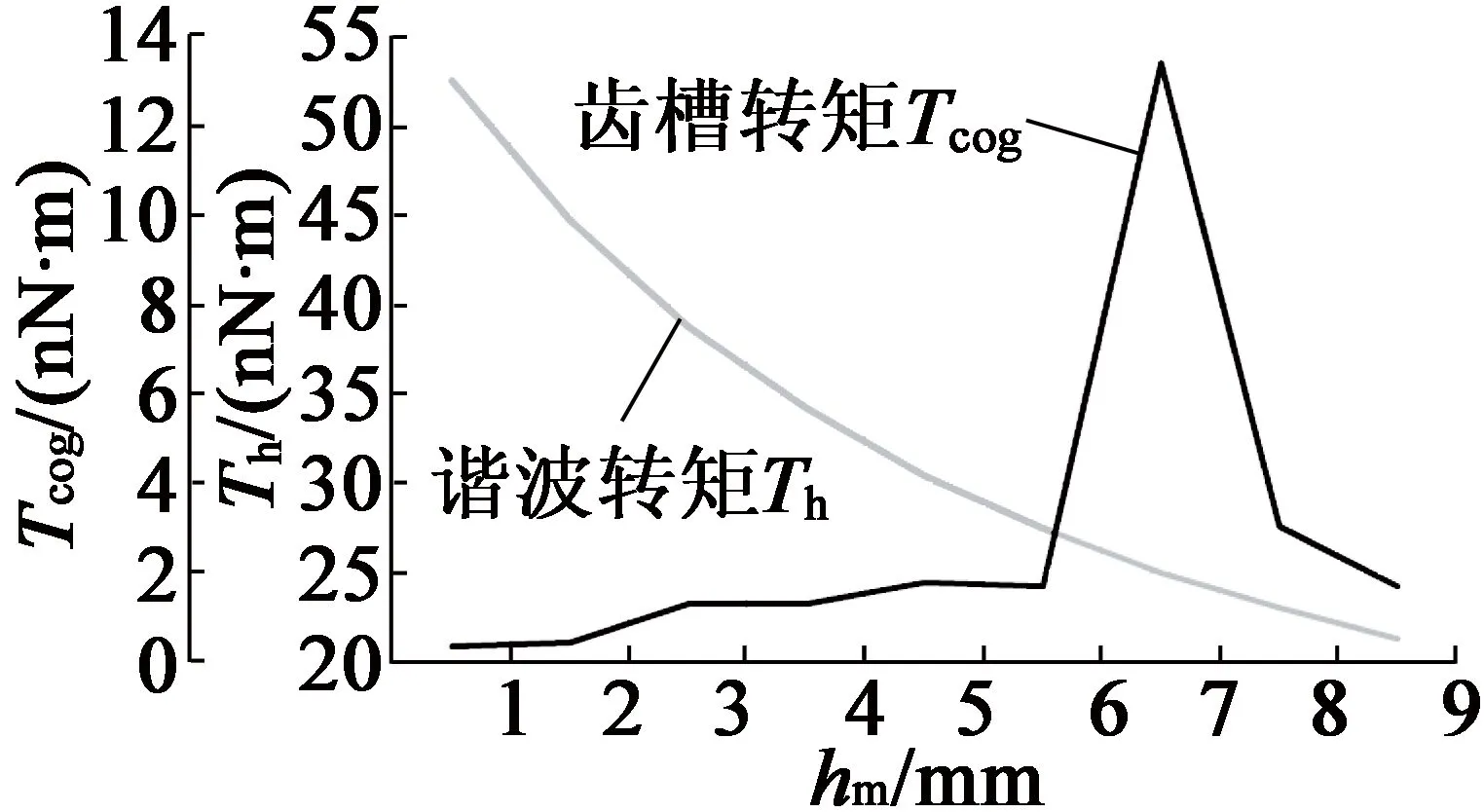
圖7 Tcog,Th與hm關系曲線

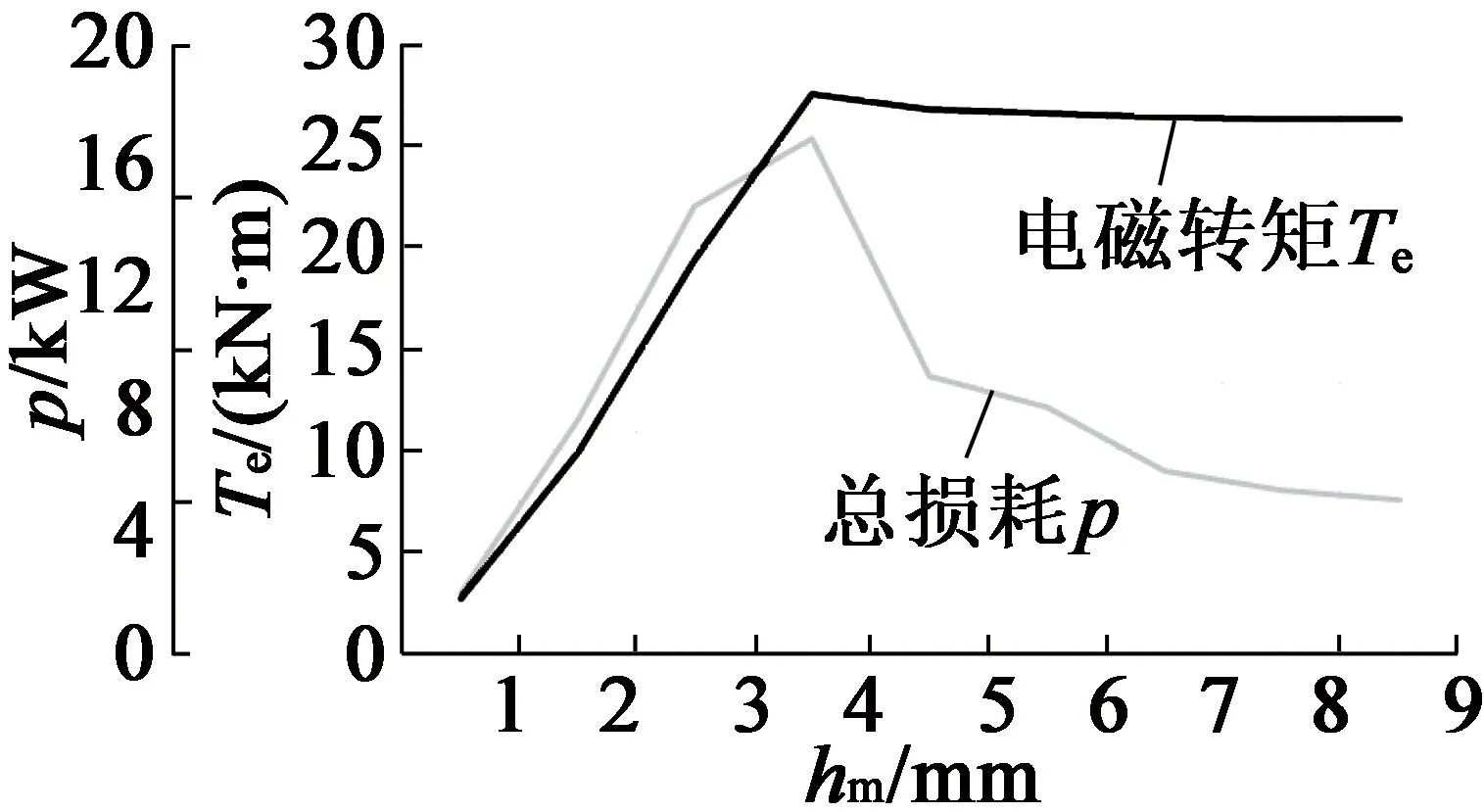
圖8 Te, p與hm關系曲線

1.1.5 定子斜槽對電機性能的影響

由表1確定主要尺寸參數，并由上文確定最優的鐵心長度、極弧系數、氣隙長度與永磁體厚度分別為0.9 m，0.785，9 mm與9 mm，在RMxprt中設計永磁同步發電機，添加斜槽寬度Nz=0～1.0 mm優化方案，可得斜槽寬度對電機齒槽轉矩與齒諧波、電磁轉矩與效率影響，如圖9、圖10所示。定子斜槽寬度與電磁轉矩和損耗成正比，與齒諧波成反比，適當增加斜槽寬度會削弱齒槽轉矩，寬度為1.0 mm時，Tcog≈0，齒諧波最少，Te最大。

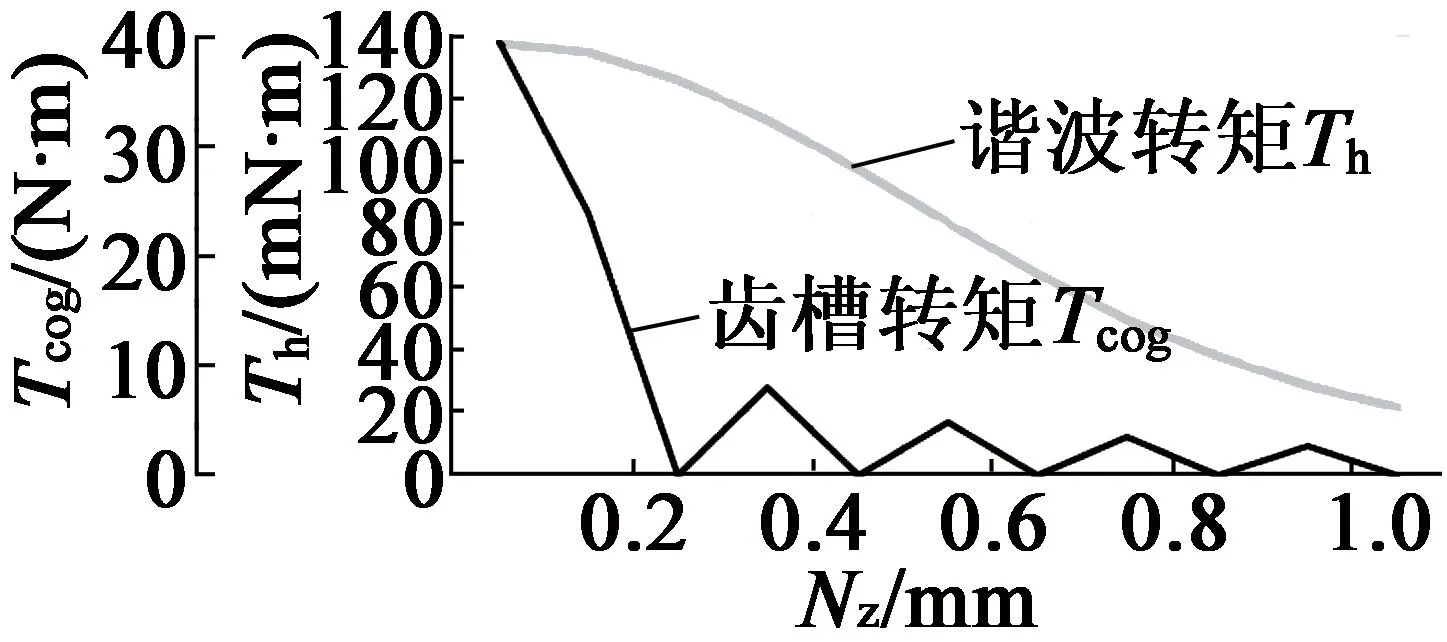
圖9 Tcog,Th與Nz關系曲線

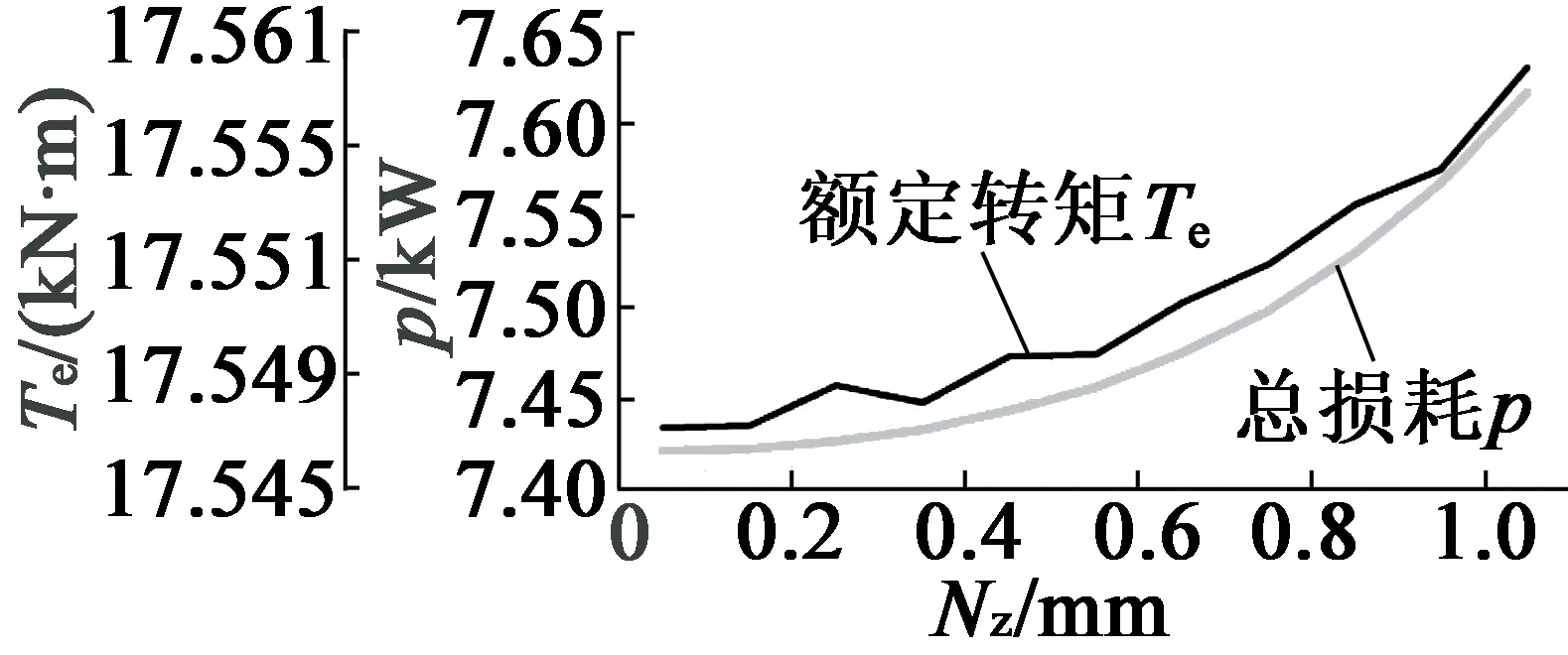
圖10 Te, p與Nz關系曲線

1.2發電機優化設計與參數計算

由上述電機性能分析，利用多變量、多目標耦合尋優設計永磁發電機結構及尺寸參數如表2所示。定、轉子采用梨形斜槽與雙向斜極，尺寸參數與繞組接線如圖11所示。

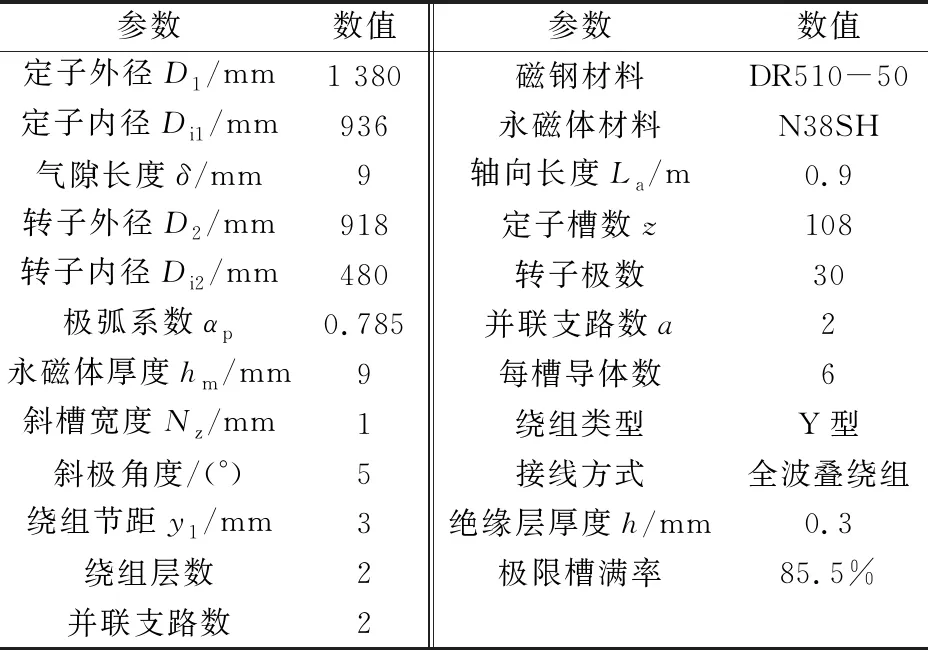
表2 360 kW/690 V，200 r/min PMSWG優化后參數

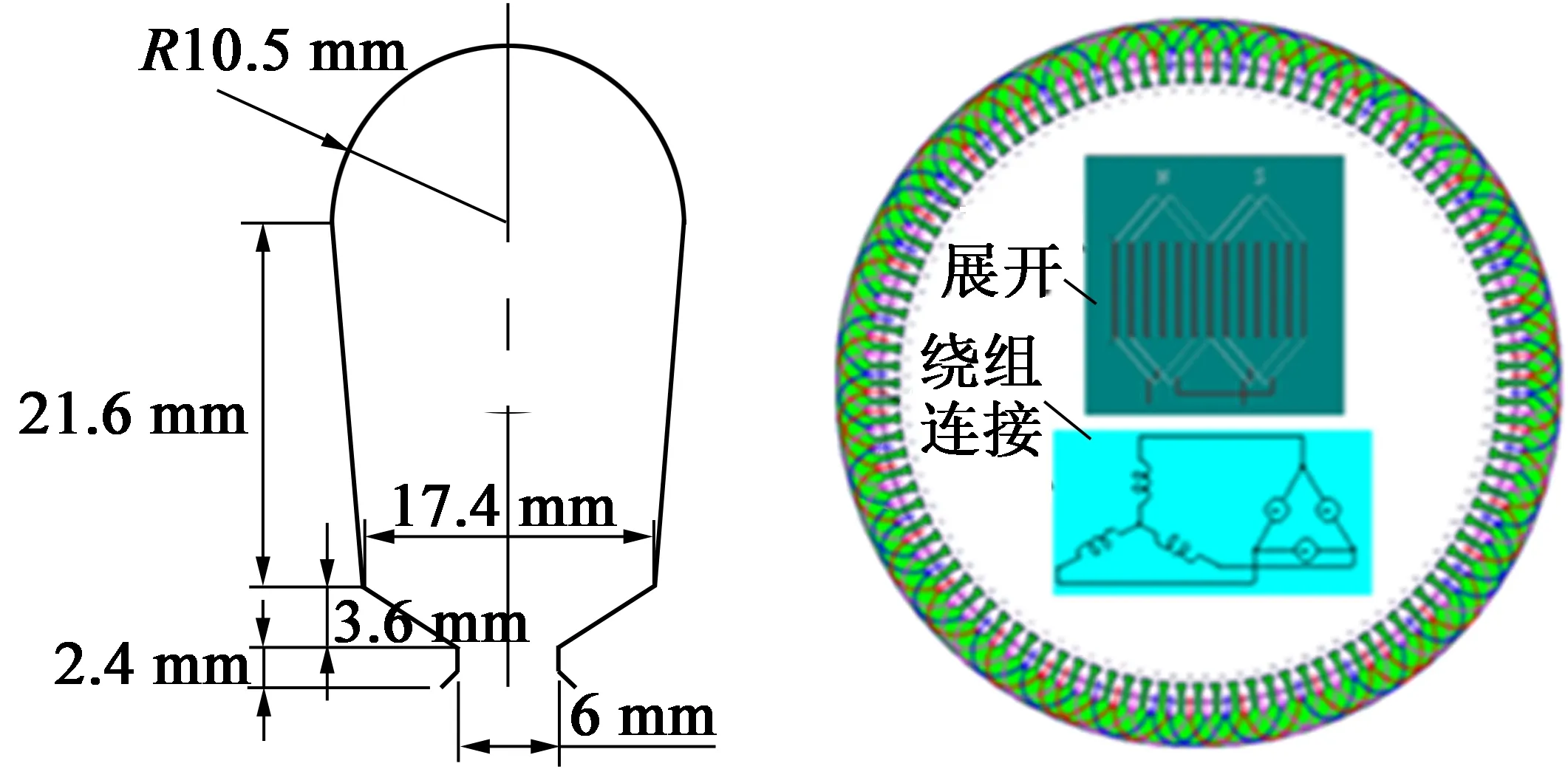
圖11 槽形尺寸與繞組接線方式

因風速變化引起該發電機轉速波動僅0.6 r/s，由似穩電路定義得電機運行在穩態。

經RMxprt設計，電機端部漏感Lσ[15]：

(4)

式中：N1為每相線圈匝數；Kdp1為繞組系數；d為線圈直線部分伸出鐵心的長度；fd為線圈端部軸向投影長度；p1為極對數。經計算，Lσ=12.6 μH。

穩態下電阻Rs[11]：

(5)

式中：ρCu為銅的電阻率；Lav為線圈半匝長度；ACu為導體截面面積。計算得到Rs=0.21 Ω。

穩態下d，q軸電感Ld,Lq[15]：

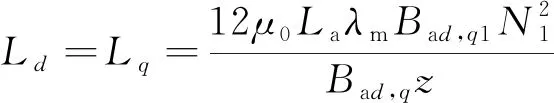
(6)

式中：Bad,q1,Bad,q為d，q軸電樞磁場的基波磁密幅值與磁密最大值；λm為相對磁導率。計算得到Ld=Lq=0.63 mH。

電機的空載總磁通[11]：

ψf=2πD2BgαpLa

(7)

計算得到ψf=1.15 Wb。

2 發電機主電路與控制建模

2.1直驅永磁風電機組的數學模型

2.1.1 風力機

由Betz理論，風力機輸出軸上機械轉矩Tm、捕獲風能能量系數CP[16]:

(8)

式中：ρ為空氣密度；λ為葉尖速比；β為槳距角；Rr為葉輪半徑；vw為風速。

由葉尖速比定義可得不同風速下發電機的最佳電角速度[16]：

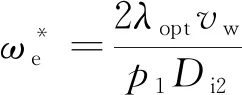
(10)

式中：λopt為式(9)極值對應最優λ值。

2.1.2 永磁同步發電機

經坐標變換，轉子磁鏈定位在d軸，則dq坐標系下永磁同步發電機數學模型[17]：

(11)

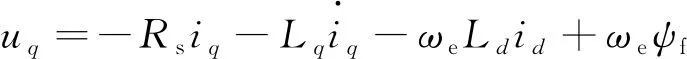
(12)

Te=3p1[ψf+(Ld-Lq)id]iq/2

(13)

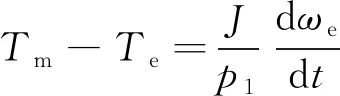
(14)

2.2發電機側系統結構與等效電路

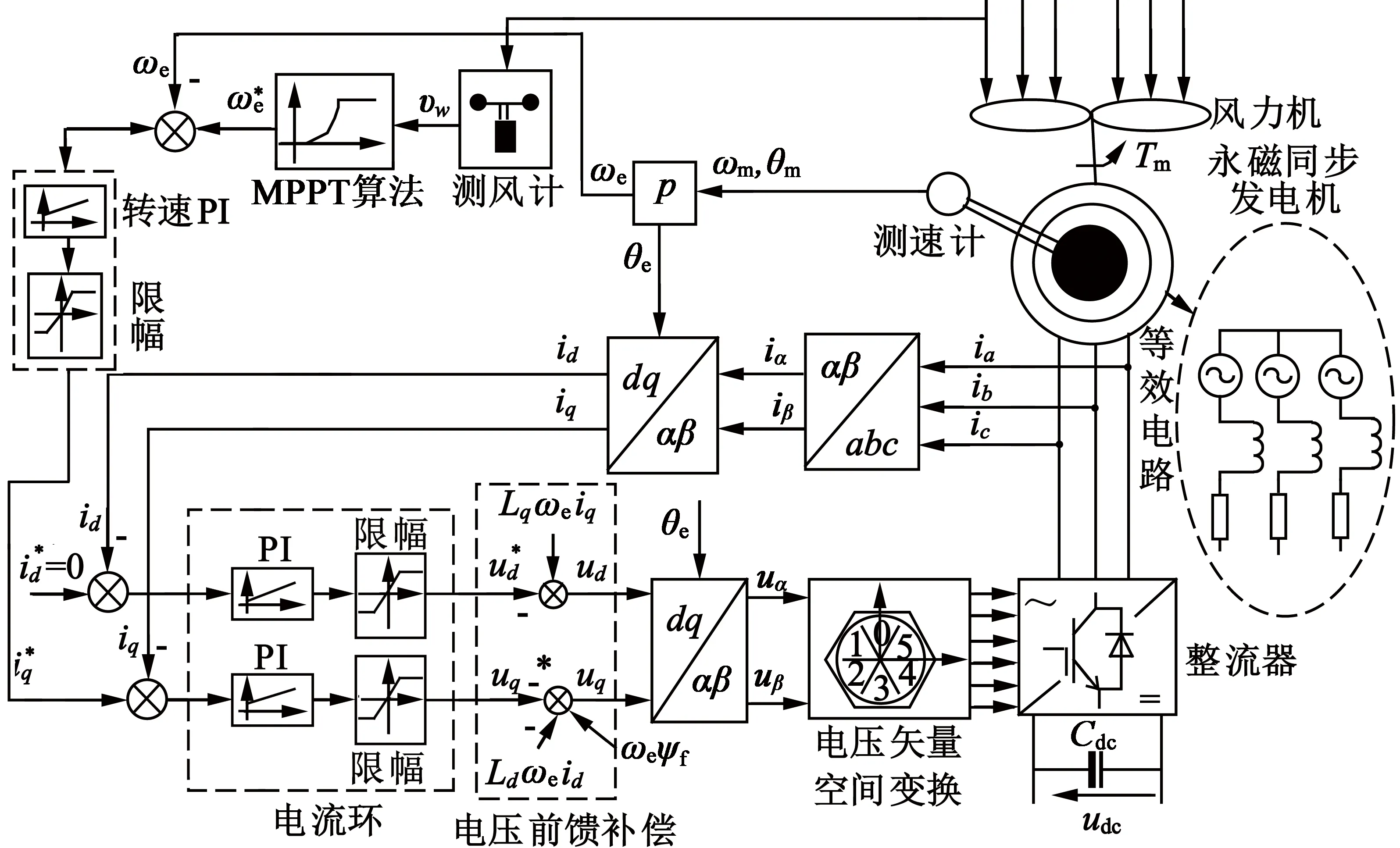
圖12 PMSWG側系統的結構

3 場路耦合仿真及分析

3.1發電機主電路與控制仿真

3.1.1 風力機

由上述分析可建立風力機仿真模型,如圖13所示。包括能量系數與轉矩模型(式(8)、式(9))、軸轉速與葉尖速比求解(式(10))。

3.1.2 主電路與控制仿真

電機設計后，由Maxwell有限元法建立電機模型，計算得電機的轉動慣量為489.449 kg·m2；由直驅永磁發電機側系統結構與等效電路，可在Simplorer下搭建主電路與控制仿真模型。由RMxprt計算，為安全考慮,選擇1 200 V/995 A IGBT作為整流電路；控制模型由轉速環PI,dq軸電流環PI，dq軸電壓前饋補償，坐標變換與電壓空間矢量變換模塊組成。

3.2仿真環境設置

為驗證360 kW/690 V，200 r/min直驅永磁風電機組在四種不同風速，采用雙閉環PI控制實現最大功率追蹤的可行性，構造由0～1 s基本風、1～3 s陣風、3～4 s漸變風、4～6 s隨機風組成的分段風速模型,如圖14，基于電機設計所構建精確模型，采用表3控制器參數進行仿真，步長為1 ms。

圖14 風速υm與機械轉矩Tm波形表3 控制器參數

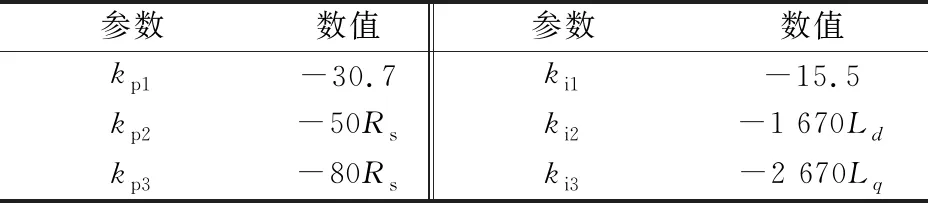
參數數值參數數值kp1-30.7ki1-15.5kp2-50Rski2-1 670Ldkp3-80Rski3-2 670Lq

表3中:kp1,ki1，kp2,ki2，kp3,ki3為轉速環與d，q軸電流環的比例與積分增益。

3.3仿真結果及分析

圖15為發電機的氣隙磁鏈波形。可知，因變風速擾動導致轉速波動，對氣隙磁鏈幅值的影響基本可以忽略，故d，q軸動態解耦參量可為穩態下的電機電感與磁鏈參量。

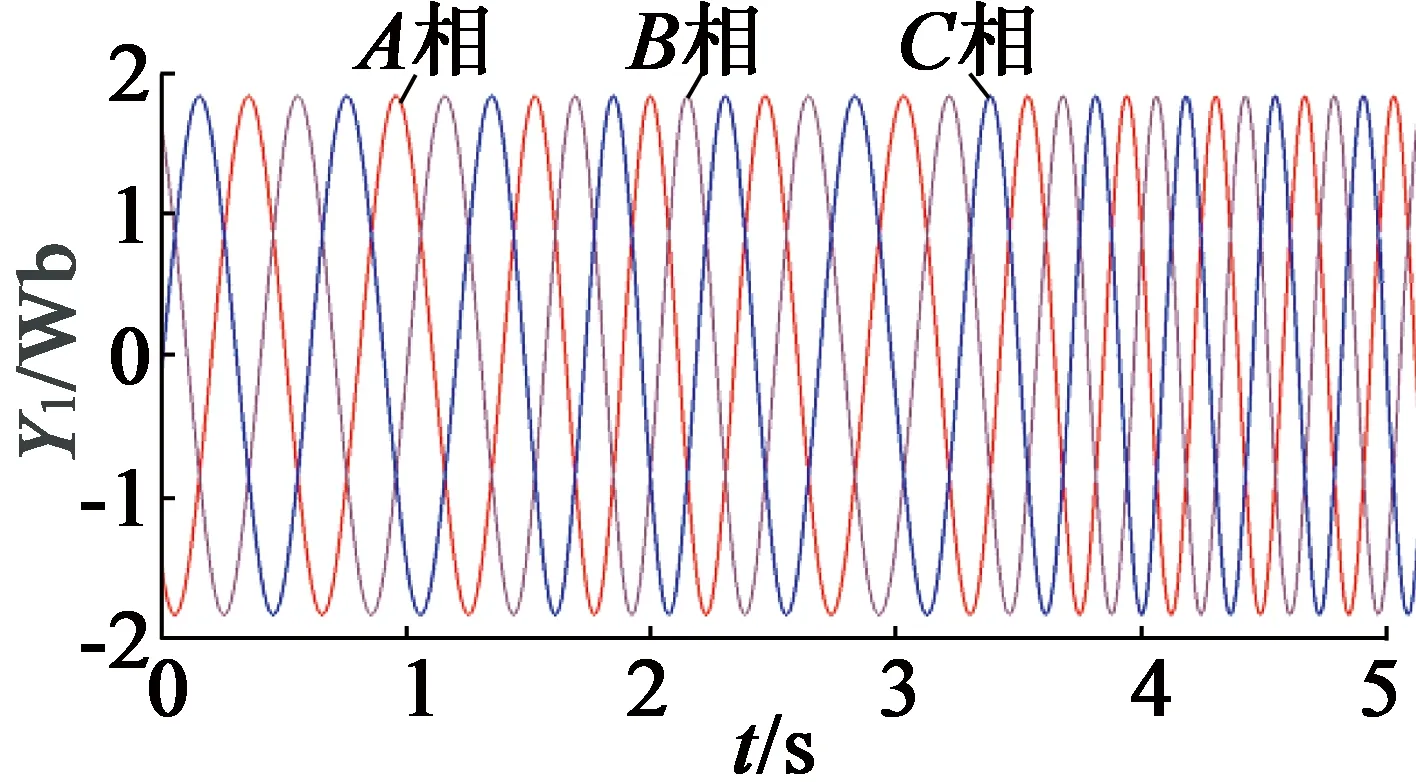
圖15 氣隙磁鏈波形

圖16為能量系數、發電機機械轉速與齒槽轉矩波形。發電機采用雙閉環PI控制，在四種不同風速下，轉速動態響應快，能量系數保持在43.8%。

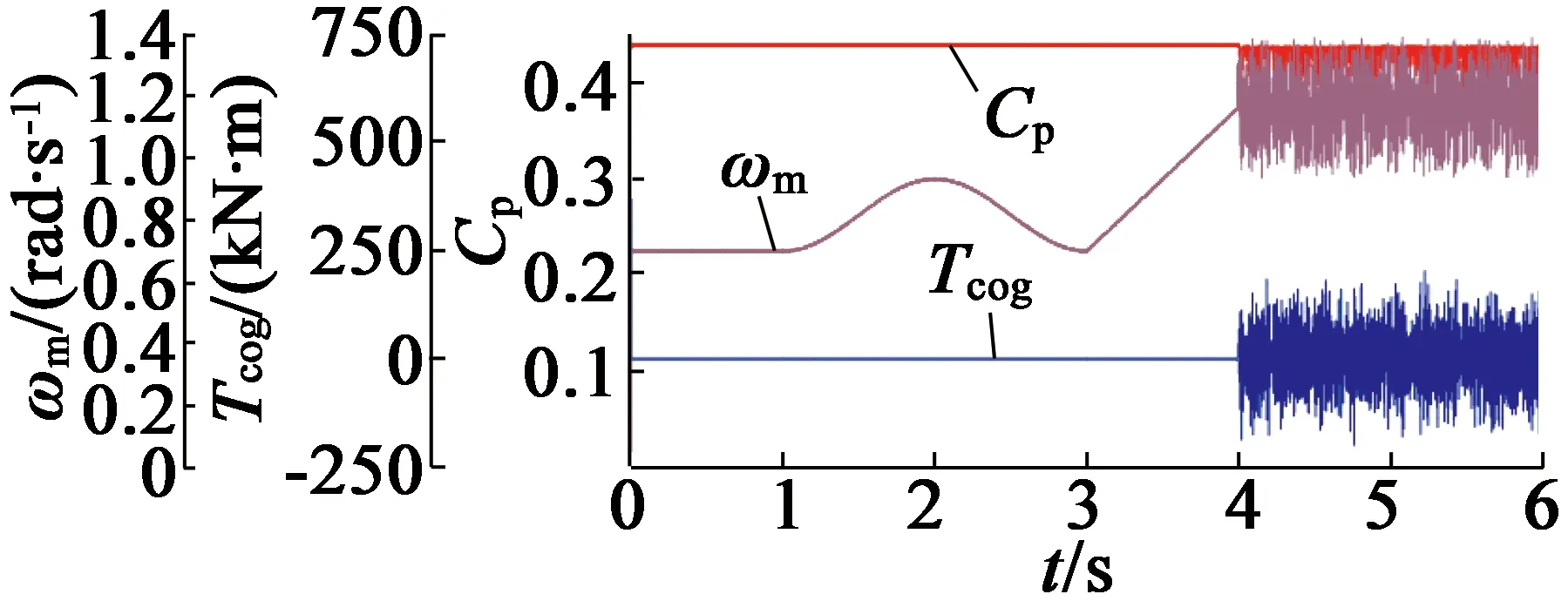
圖16 能量系數Cp、發電機機械轉速ωm與Tcog波形

圖17、圖18為發電機定子電流、轉矩與功率波形。可知，通過調節d，q軸電流，使定子電流波形為正弦波，其幅值、轉矩與功率快速跟隨風速變化，從而實現最大功率追蹤。

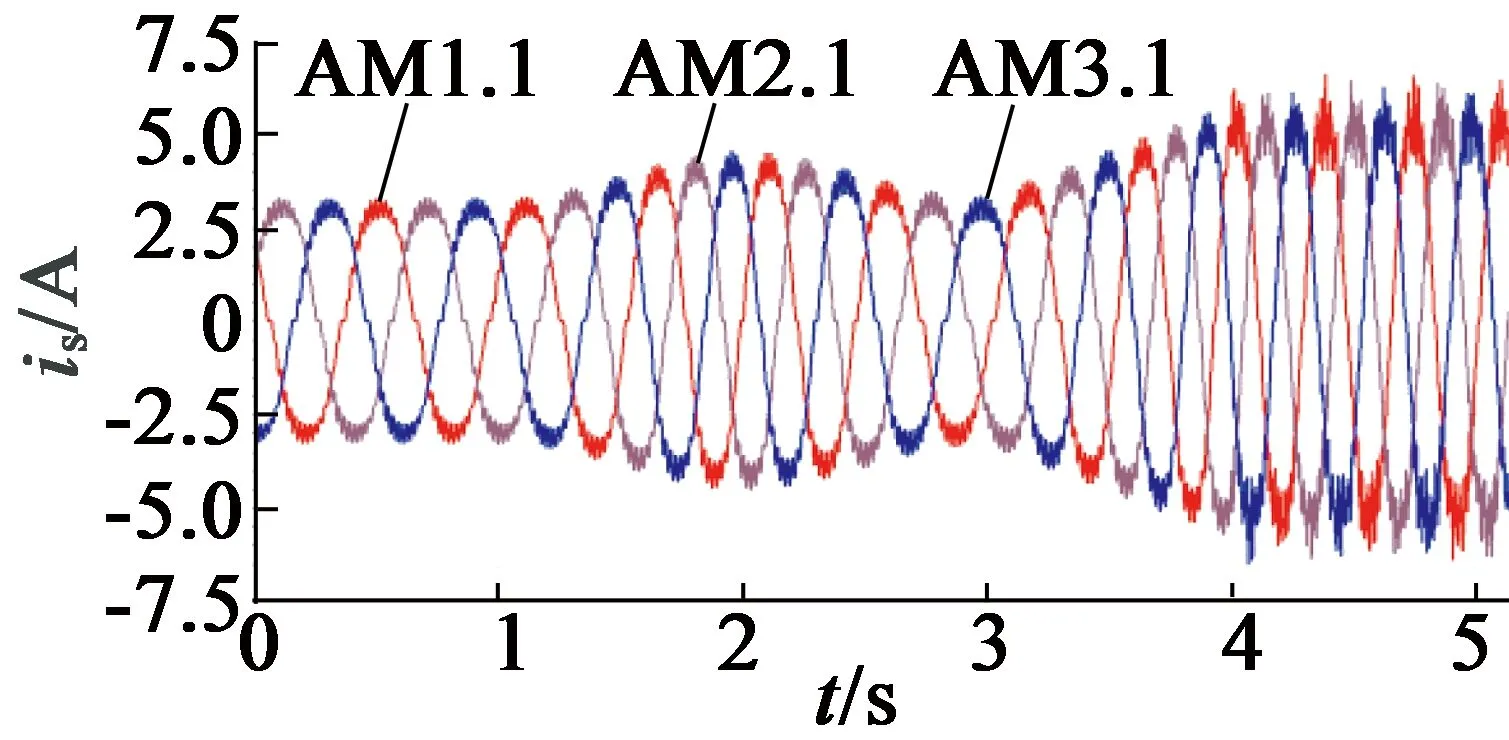
圖17 定子電流波形

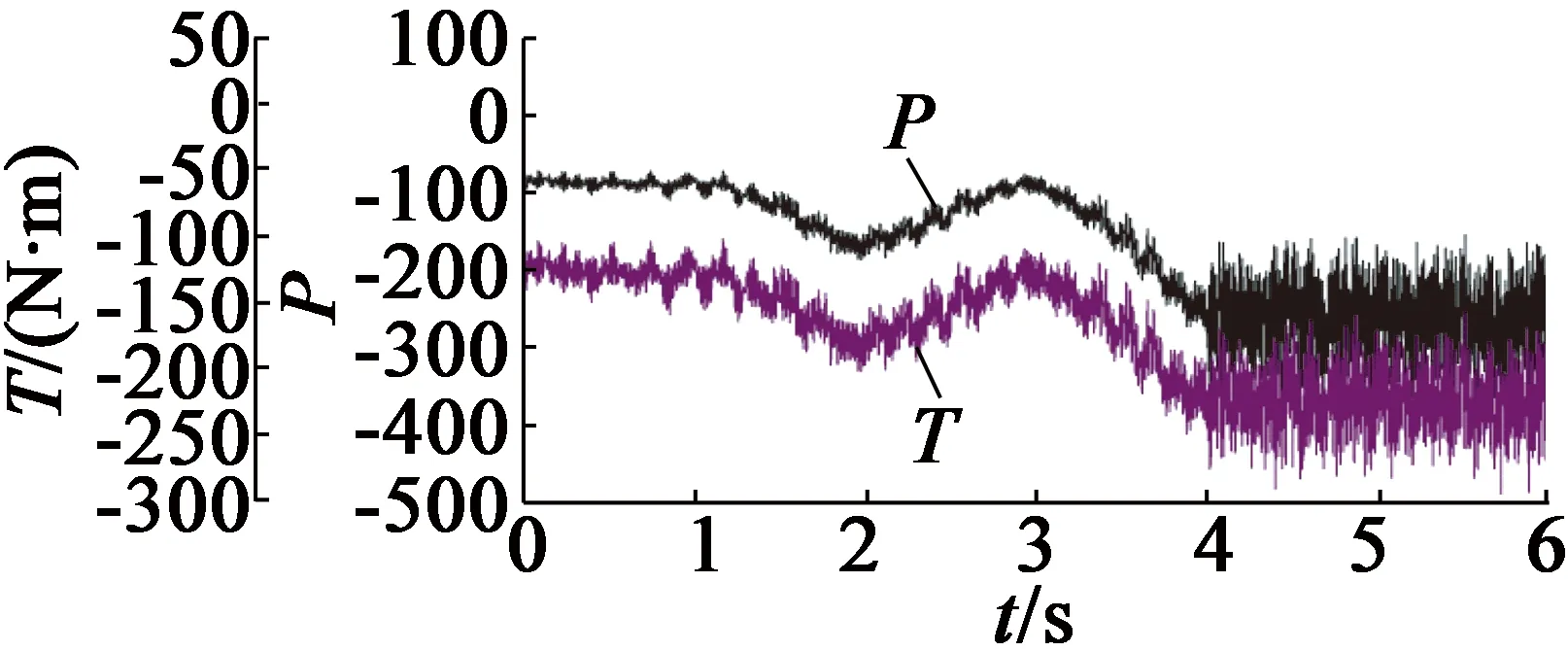
圖18 發電機轉矩與功率波形

由圖16、圖17可見，因風速的高頻瞬變干擾，導致PI控制的魯棒性降低，使能量系數與電流曲線表現為隨風速波動劇烈程度增加而增大脈動波形，并產生較大齒槽效應，體現了場路耦合仿真結果的高可靠性。

4 結 語

本文基于電機相似性，針對斜極/斜槽結構的360 kW/690 V，200 r/min永磁發電機性能受多參量耦合影響，研究了利用多變量、多目標耦合優化其尺寸參量，以提升電機效率與轉矩，削弱齒槽轉矩與諧波；針對PI控制的模型依賴性、兆瓦級風電調試成本高、研制周期長，提出利用有限元法精確建立電機模型，利用場路耦合仿真模擬發電機在四種不同風速擾動、電磁耦合影響參數攝動共同作用下的動態起動過程，并給出了仿真分析，驗證了系統實現最大功率追蹤可行性，有效提高了仿真結果的可靠性，從而有效降低了硬件調試難度，縮短了硬件研制周期。